缜密思考防失误，跳出陷阱有妙招

江苏海门三星初级中学 丁 慧

缜密思考防失误，跳出陷阱有妙招

江苏海门三星初级中学 丁 慧

数学离不开解题，解题的过程实质是一个通过不断的探索由未知向已知转化的过程，这个过程需要透过现象有效抓住问题的本质。然而在解题过程中，学生常常因为对概念、法则、定理、公式、原理、方法等认识不足或偏差，导致在解决数学问题时出现相反或是不完全的结果，从而陷入解题陷阱。如何有效走出解题的误区和盲区？本文提出四种解决方法，与同行研讨。

一、使用概念要明辨，跳出概念陷阱题

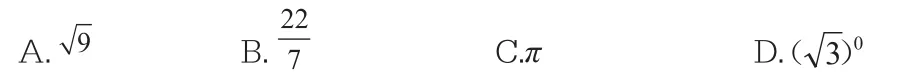
本题的正确答案是C，然而学生各种答案都有。其主要原因是不能深刻理解无理数的概念，选A的是没有理解二次方根的意义，选B的是把与π等同了，选D的是因为没有理解零指数幂的意义。

在解答概念类试题时，一定要仔细辨析试题待求的问题，在准确用好概念的前提下再对试题进行解答。如本题中要针对这些错误，在教学中加强无理数是无限不循环小数，不是带根号的数就是无理数等概念的辨别，告诉学生学会“数看实质，式看形式”的方法技巧。

二、作图用图要正确，跳出图解陷阱题

例2 已知二次函数y=x2-2x-3，当0≤x≤3时，y的最大值与最小值分别为（ ）

A.0，-4 B.0，-3 C.-3，-4 D.0，0

本题的正确答案是A，但本题有很多学生选B选项，学生简单地把自变量分别为0和3的时候代入，求出y的值，而没有考虑二次函数取得最小值时的自变量在条件所给的区间内。

图解问题的关键是正确作图，对于二次函数而言，一些关键点的认识尤其重要。如本题中，我们要认真区分定义域为R和定义域为特定区间的函数图象的区别，在此基础上再分别讨论函数的最值问题。

三、条件性质要周全，跳出隐含陷阱题

例3 若关于x的方程kx2+2x-1=0有两个不相等的实数根，则k的取值范围是（ ）

A.k＞-1 B.k≥-1 C.k≠0 D.k≥-1且k≠0

本题正确答案是D,但题目中一元二次方程的这一隐含条件很容易被忽视，很容易导致漏解，从而导致错解，本题应首先考虑二次项系数不为0这一条件。

数学中的很多问题都在一定条件下成立，这就需要学生在审题时要认真读题、挖掘题目内在隐含的条件。如在本题中，对方程有两个不相等实数根的认识是指方程为一元二次方程，这一点是解决问题的关键。

四、推理论证要严谨，跳出定式陷阱题

例4 若关于x的函数y=ax2+3x-1与x轴有唯一交点，求a的值。

解析：当a=0时，函数是一次函数，所以与x轴有唯一交点。

当a≠0时，函数是二次函数，那么当时，有唯一交点，

即b2-4ac=0，32-4×a×(-1)=0，

因此a的值为0或

本题的推理论证建立在对函数的正确理解上，由于a的值没有确定，所以函数既可以是二次函数，也可以是一次函数，而学生的思维定式就只把函数当成二次函数来解题。所以解题时要认真进行对比分析，打破思维定式。

五、运算过程要适切，跳出运算陷阱题

例5 鄂州市化工材料经销公司购进一种化工原料若干千克，价格为每千克30元，物价部门规定其销售单价不高于每千克60元，不低于每千克30元，经市场调查发现：日销售量y（千克）是销售单价x（元）的一次函数，且当x=60时，y=80；当x=50时，y=100。在销售过程中每天还要支付其他费用450元。

（1）求出y与x的函数解析式，并写出自变量x的取值范围；

（2）求该公司销售该原料日获利W（元）与销售单价x（元）之间的函数关系式；

（3）当销售单价定为多少元时，该公司的日获利最大？最大获利多少元？

解析：（1）根据题意设y=kx+b，则有解得k=-2，b=200。

所以y=－2x+200（30≤x≤60）。

（2）由题意得：W=(x－30)(－2x+200)－450=

－2x2+260x－6450=－2(x－65)2+2000。

（3）W=－2(x－65)2+2000，

因为30≤x≤60，

所以当x=60时，W有最大值为1950。

所以当销售单价为60元时，该公司日获利最大，为1950元。

实际问题中自变量常常有相应的取值范围，如果忽视实际取值范围，不仅题目结果出现问题，而且也和实际不切合。如本题中，若不注意取值范围范围为，本题最多的错误就是学生配方后直接得出在单价为65元时最大利润为2000元，没有考虑自变量的取值范围为30≤x≤60，从而掉入陷阱中。

变式（2016南通） 如图，平面直角坐标系xOy中，点C（3，0），函数y＝（k＞0，x＞0）的图象经过平行四边形OABC的顶点A（m，n）和边BC的中点D。

（1）求m的值；

（2）若△OAD的面积等于6，求k的值；

（3）若P为函数y＝（k＞0，x＞0）图象上的一个动点，过点P作直线l⊥x轴于点M，直线l与x轴上方的平行四边形OABC的一边交于点N，设点P的横坐标为t，当时，求t的值。

本题的错误主要出现在第（3）问，很多学生没有注意t的取值范围。过动点P作直线l⊥x轴，直线l与x轴上方的平行四边形OABC的一边交于点N，这就意味着P的横坐标t的取值是有范围的，t的取值范围是0＜t＜5，超越这个范围的t的都是不切合的。解决这个问题的关键就是从交点的位置与相应的t的取值范围去思考，在OA、AB、BC边上时，点P与点N的相对位置表示出线段PN、PM的长度，继而代入求解，求出结果后再回到开始的取值范围，把不符合的数值删去。

综上，虽然数学中的陷阱题往往以假乱真，但我们只要熟悉跳出陷阱的妙招，就一定能有效避免无谓失分。