弹体破片分布及破碎性系数计算*

郭 超, 宫小泽, 李向东

(1 南京理工大学机械工程学院, 南京 210094; 2 中国白城兵器试验中心, 吉林白城 137001)

弹体破片分布及破碎性系数计算*

郭 超1, 宫小泽2, 李向东1

(1 南京理工大学机械工程学院, 南京 210094; 2 中国白城兵器试验中心, 吉林白城 137001)

为了研究弹体破片分布与材料、炸药、壳体等的影响关系,以Mott模型为基础,通过切片的方法对弹体进行了理论分析。分析了破碎性系数B的主要影响因素,通过量纲分析得到了破碎性系数B计算公式。通过该公式得出了13 mm壁厚弹体破碎性系数,且得到破片数和破片质量分布,并与试验数据进行对比分析误差小于5%,是因为回收率和端盖的影响。提高破片回收率和排除端盖的影响,该破碎性系数计算公式可用于弹体破碎性分布计算。

破碎性系数;破片分布;破片数;破片质量

0 引言

国内外对非预制破片的研究,使用最广泛的是40年代的Mott[1]模型和70年代的Payman[2]模型,而破碎性试验是测定破片数目、质量分布得到分布规律的一种常用试验方法。

吴成等[3]通过仿真软件,对小口径榴弹起爆后壳体膨胀和破片形成过程进行了计算机模拟仿真;黄经伟[4-5]等通过破碎性试验研究了大口径榴弹自然破片分布规律;宋文渊[6]通过有限元建模对自然破片进行了建模分析。他们对破片数目及质量分布进行了研究,并得到了分布规律,同时也验证了Mott模型的适用性,但是对于Mott模型中与材料相关的参数并没有给出相应的分析。甄建伟、安振涛等[7]研究了弹丸破碎时壳体半径与破片大小及数目的关系,得出了随着圆环半径的增大,破片数目成线性增长的规律,但是并没有考虑壳体厚度的影响。陈醇[8]等研究了四种弹体材料对破片形成的影响,定性得出了随着抗拉强度的增大破碎程度加深的结论,但是并没有定量分析出具体变化关系。

文中基于试验的基础上,通过Mott模型研究弹丸壳体材料、壳体厚度、装药及半径等影响因素对弹丸破碎性的影响,并对Mott模型中破碎性系数进行了研究,建立关于材料破碎性系数与影响因素之间的计算方程,并对结果进行评估分析。

1 破碎性试验

1.1 试验设计

图1所示为试验模拟弹结构,表1给出了试验模拟弹壳体厚度tk、壳体质量mk、炸药当量系数f、炸药质量mz、炸药内径d等相关参数,壳体材料为50SiMnVB。

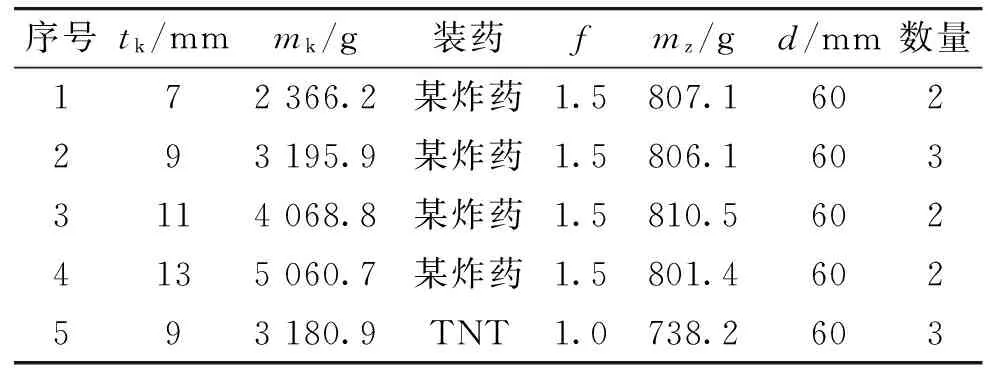
表1 模拟弹参数

1.2 试验数据

不考虑质量小于0.1 g或0.3 g的破片,将回收的破片逐个称重分组,得到了破片数及破片质量分布。

1)试验模拟弹数据

分组处理,得到试验破片统计表如表2及表3所示。

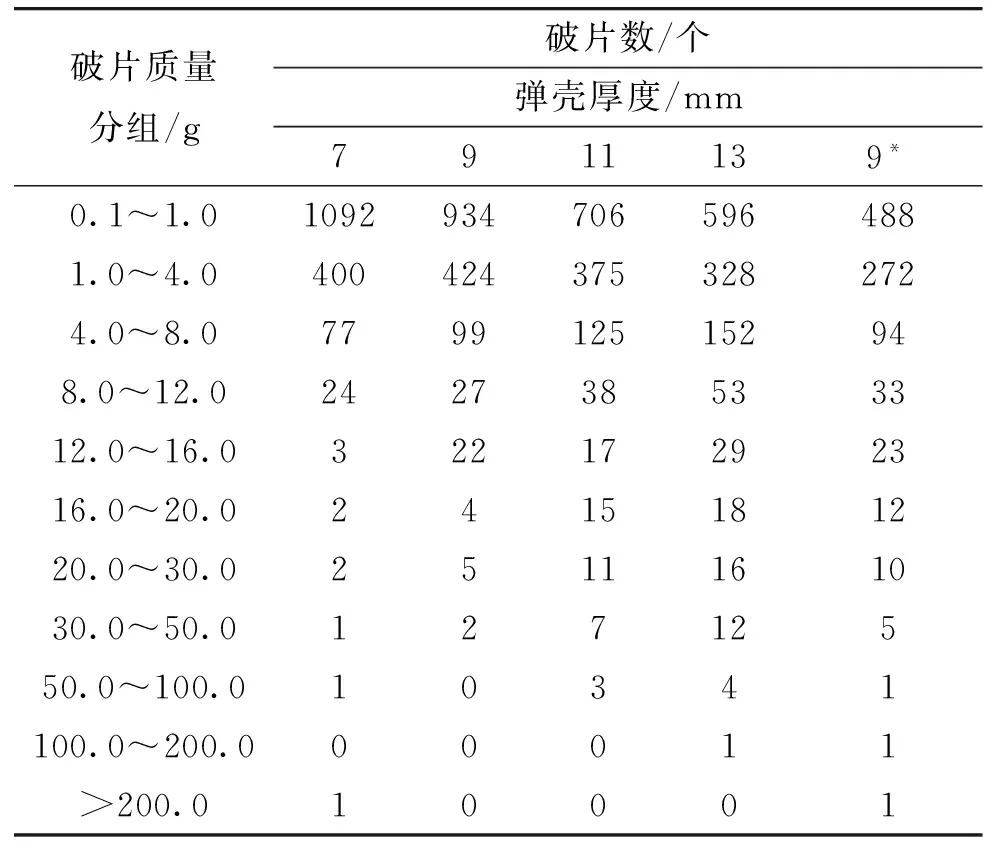
表2 破片数统计表

注：*表示弹壳内装药TNT，未注*表示某装药。

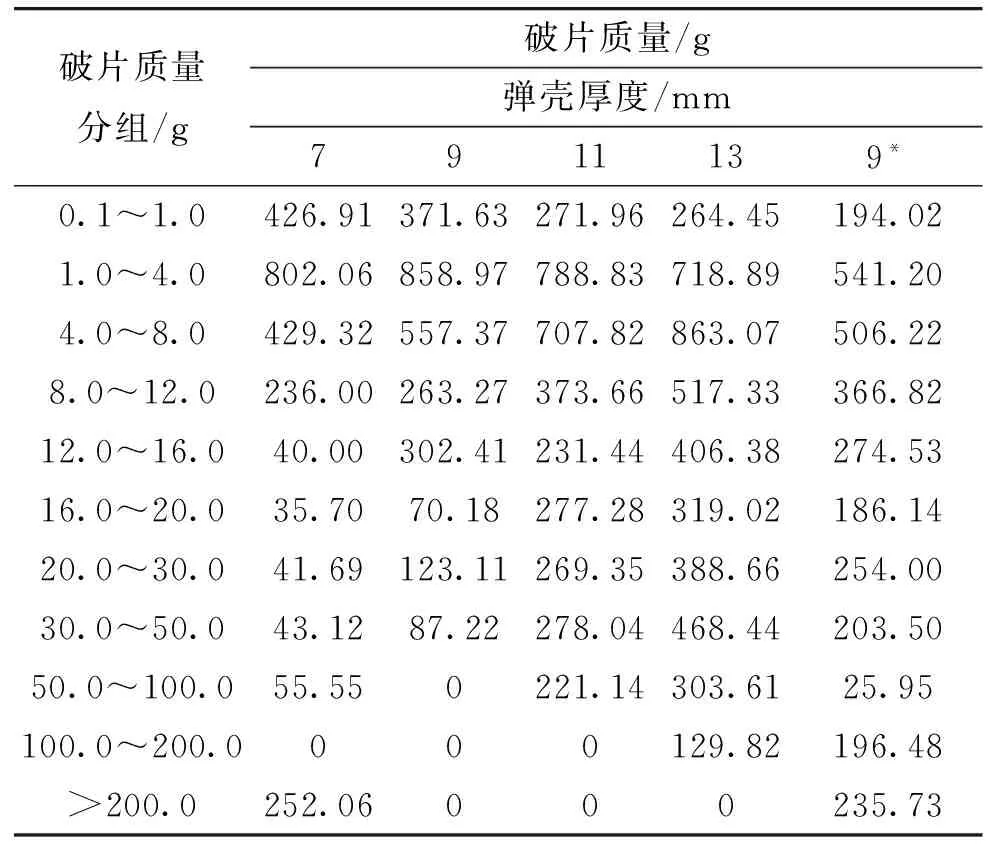
表3 破片质量统计表

注：*表示弹壳内装药TNT，未注*表示某装药。

2)某坦克炮杀伤榴弹数据

壳体材料为58SiMn的某坦克炮杀伤榴弹,破片数及破片质量分布如表4所示(该数据由其他实验基地提供)。

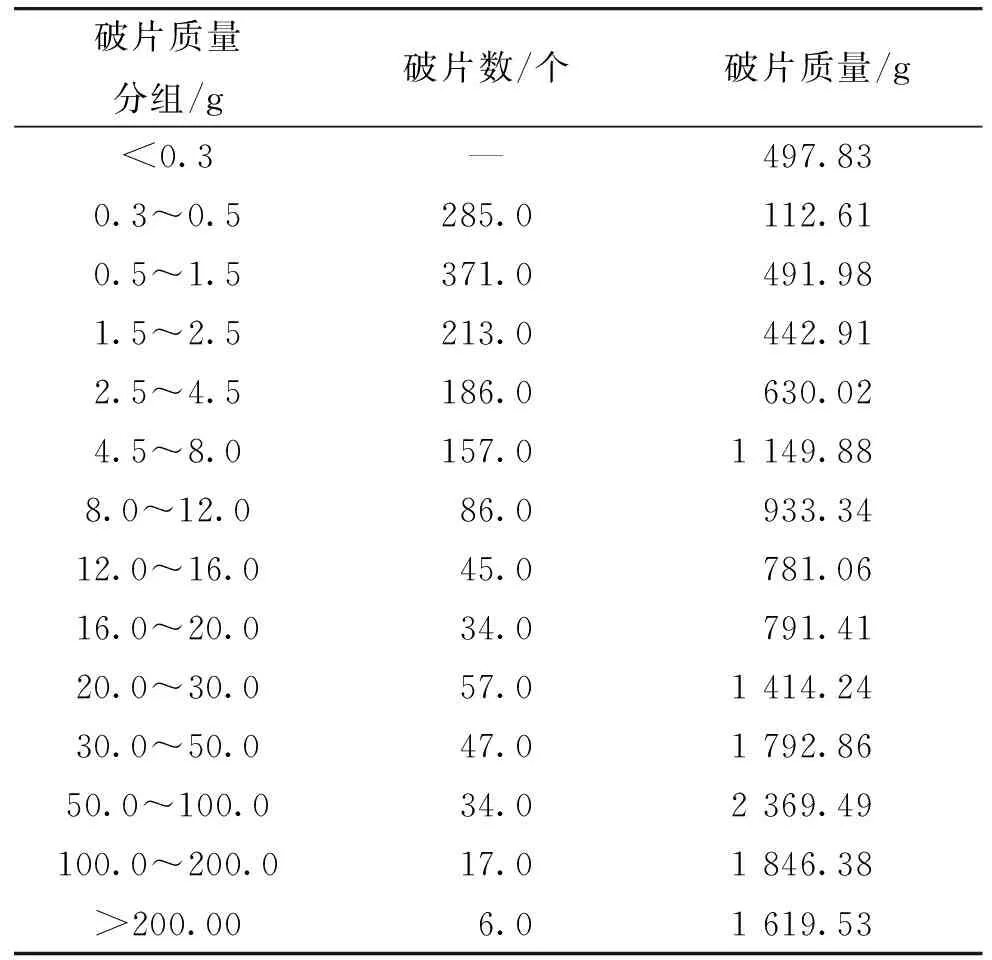
表4 某坦克炮破片分布表

1.3 理论分析

1.3.1 单元格划分

沿着弹丸轴线垂直方向,将弹丸切割成不同单元格,划分原则是将壁厚相近或相似部分划为一个单元格(不考虑上下底部分),如图2所示。

1.3.2 理论计算模型

于第i个单元格,破片质量特征参数计算公式为[9]:

(1)

则由Mott公式[1]计算第i个单元破片总数为:

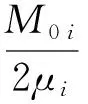
(2)

第i个单元格,单个破片质量大于mj时的破片累积数及累积质量为:

(3)

(4)

1.3.3 破碎性系数分析

累加所有单元格,可求得模拟弹单个破片质量大于mj的破片累计数N(>mj)和破片累计质量M(>mj)。

则在质量区间mj～mj+1,破片数与破片质量为:

N(mj～mj+1)=N(>mj)-N(>mj+1)

(5)

M(mj～mj+1)=M(>mj)-M(>mj+1)

(6)

假设破片在质量区间mj～mj+1的实际统计数为N实(mj～mj+1),实际统计质量为M实(mj～mj+1),则破片数残差百分比与破片质量残差百分比分别为:

式中:N实及M实表示回收的真实破片总数及破片总质量。

则得到残差平方和S为:

(9)

采用最小二乘法对系数B进行分析,残差平方和S最小时得到最佳系数B。根据我国杀伤破片对有生力量的杀伤标准[10]:动能大于98 J,破片质量不小于1 g,而实际有效杀伤破片质量为1.0～50.0 g,因而取质量为1.0～50.0 g的破片进行分析。

分析某炸药、壳体壁厚7 mm、9 mm、11 mm及13 mm的模拟弹,破碎性系数B与残差平方和S变化关系如图3所示,得到破碎性系数B如表5。

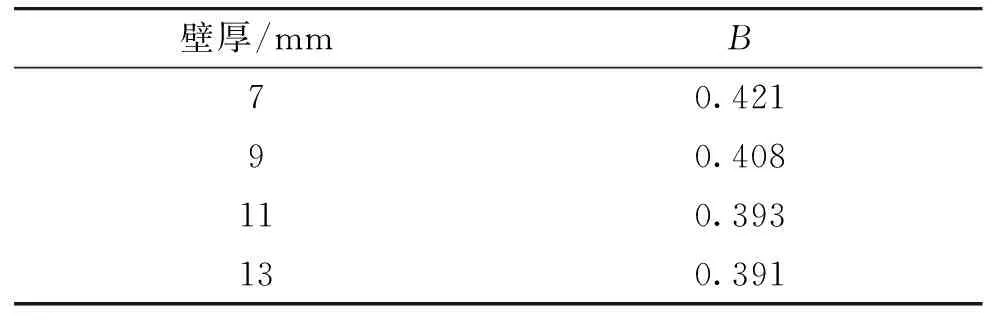
壁厚/mmB70.42190.408110.393130.391

同理,分析TNT装药、壁厚9 mm模拟弹,破碎性系数B与残差平方和S的变化关系,得到破碎性系数B为0.507;某坦克炮破碎性系数B为0.346。

1.4 破碎性系数分析

再次，要有底线。中国共产党从民主革命时期走到现在，经历了各种艰难困苦，特别是在和平年代，社会主义市场经济的飞速发展使一些不良思想有一定抬头，这就要求思想的坚定和政治信仰的坚定就非常重要了。所以，这就意味着每一名党员必须要牢固树立底线意识，作为青年学生，在日常工作、生活中，我始终坚守底线，要有自己的原则，坚持自己的政治信仰，要立志为社会主义事业贡献自己的力量。

1.4.1 基本假设

假设破碎性系数B的影响因素主要为厚径比(壳体壁厚与炸药直径)、质量比(壳体质量与炸药当量质量)、密度比(壳体密度与炸药密度)和壳体极限抗拉强度,经量纲分析,得到基本公式:

(10)

式中:k1、k2、k3、k4、k5为相关系数;tk/De为厚径比;ρk/ρz为密度比;mk/mz为质量比,其中mz=f·m,f为炸药的TNT当量系数,m为炸药质量(g);σb为壳体极限抗拉强度(MPa)。

1.4.2 相关系数求解

表6给出了材料及材料强度P(MPa)以及得到的最佳破碎性系数B值。

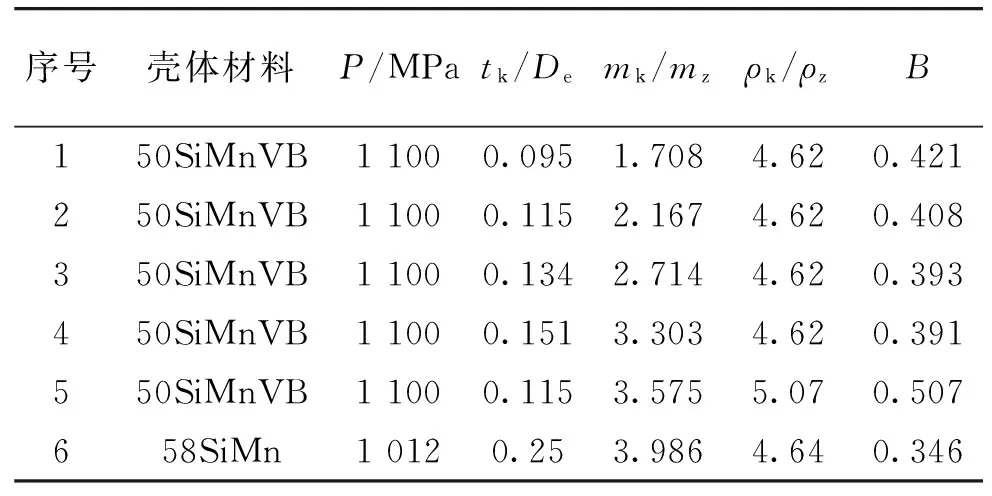
表6 相关参数

将表6序号为1、2、3、5、6(序号4用于结果检验)的数据代入式(10),通过Matlab求解,得到相关参数值如表7所示。

表7 相关系数值

则破碎性系数B的计算公式为:

(11)

1.5 破碎性计算

1.5.1 误差分析

理论分析得到最佳破碎性系数B为0.391(见表6),将表6序号4各项参数代入式(11)求得破碎性系数为0.378,相对误差为3.32%。

1.5.2 结果对比分析

将计算所得B=0.378及理论所得B=0.391代入式(1)～(6),得到破片数、破片质量分布结果,并与真实数据进行对比(见图4～图6)。

由图4和图5分析可得,在0.1～4.0 g之间,计算所得破片数及破片质量与理论破片数及破片质量相差不大,但较试验破片数及破片质量偏大,其中1.0～4.0 g之间最为明显,破片数相差100左右,破片质量相差200 g左右。分析原因主要是破片回收率引起,小质量破片回收较为困难;而在4.0～12.0 g之间,三者相差不大,计算所得数据可反映试验分布情况;12.0 g以后,试验数据较计算值及理论值偏大,且破片质量相差更为明显。分析原因为试验数据中包含有端盖的影响,端盖产生较多大质量破片,而计算数据中不考虑端盖影响,所以计算值和理论值偏低。

但是从图6分析来看,在0.1～50 g区间之间,破片平均质量相差不大。因而,计算所得破片的大小能够反映真实破片的大小。

总之,提高试验的回收率及减小端盖的影响,计算数据与真实数据将更接近。所以,计算所得破片数及破片质量分布规律,可用于计算弹丸破碎性分布。

2 结论

1)结合理论与试验数据,通过Mott模型及最小二乘法,得到模拟弹破片分布规律及理论破碎性系数。

2)研究了破碎性系数与壳体材料、壳体厚度、装药及半径等影响因素的关系,并得到了破碎性系数的相关计算方程。

3)使用该方程进行了破碎性计算,并对计算所得数据、理论分布数据及试验数据进行了对比分析,回收率造成小质量破片的偏差而端盖造成大质量破片的偏差,但是破片平均质量分布即破片大小分布较吻合。所以提高试验的回收率及减小端盖的影响,该破碎性系数方程可用于计算弹丸破碎性分布。

[1] MOTT N F, LINFOOT E H. A theory of fragmentation：Ministry of supply: AC 3348[R]. [S.l.:s.n.],1943.

[2] WALSH B. The influence of geometry on the natural fragmentation of steel cylender： N73-25930[R]. [S.l.:s.n.],1974.

[3] 吴成, 艾东明, 李京. 小口径榴弹破片质量分布规律计算模型 [J]. 弹箭与制导学报, 2002, 22(2): 35-37.

[4] 黄经纬, 李文斌, 郑宇, 等. 大口径榴弹自然破片形成过程 [J]. 兵工自动化, 2013, 32(11): 20-23.

[5] 黄经纬. 破片式战斗部破片规律及破片对步兵战车的侵彻作用研究 [D]. 南京: 南京理工大学, 2014.

[6] 宋文渊. 杀爆弹战斗部自然破片有限元建模分析 [J]. 弹箭与制导学报, 2008, 28(3): 121-122.

[7] 甄建伟, 安振涛, 陈玉成, 等. 弹丸破碎时壳体半径与破片大小和数目的关系仿真 [J]. 弹箭与制导学报, 2010, 30(6): 95-97.

[8] 陈醇, 李伟兵, 王晓鸣, 等. 弹性材料性能对破片形成的影响 [J]. 高压物理学报. 2014, 28(5): 611-616.

[9] 陈醇. 三代炸药爆炸加载下战斗部壳体形变规律及破片性能研究 [D]. 南京: 南京理工大学, 2015.

[10] 李向东, 杜忠华. 目标易损性 [M]. 北京: 北京理工大学出版社, 2013: 38-61.

CalculationofFragmentationDistributionandFragmentationCoefficientofProjectile

GUO Chao1, GONG Xiaoze2, LI Xiangdong1

(1 School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China; 2 Baicheng Ordnance Test Center of China, Jilin Baicheng 137001, China)

In order to study the influence relationship between fragment distribution and materials, explosive, shell and so on, based on Mott model, theoretical research was carried out by slice method. The main influencing factors of the fragmentation coefficientBwere analyzed, and the formula of fragmentation coefficientBwas got by dimensional analysis. The fragmentation coefficient with 13 mm thickness and fragment quantity and fragment mass were obtained by the formula. Compared with experimental data, the analytical error of the fragment coefficientBcalculated by the formula was less than 5%, because of the influence of recovery rate and end cap. This formula could be used for the distributed computing of projectile brokenness by improving fragment recovery rate and excluding the influence of the end cap.

fragmentation coefficient; fragment distribution; fragment quantity; fragment mass

TJ410.1

A

2016-05-17

郭超(1990-),男,四川绵阳人,硕士研究生,研究方向:兵器工程。