红色文化在高中数学教学中的运用
2017-10-30何远红
何远红
摘 要
按照当今社会主义荣辱观要求,现代教育越发注重教学与红色文化的有机结合,越发注重在各科教材以及对应题目中渗透红色内容。数学是高中阶段教学重要内容,有效开展教学不仅能提高学生成绩,更能在很大程度上提升学生各项优秀思维能力,对学生发展有很大帮助。有效将红色文化渗透入高中数学教学中能加强学生对红色文化的认知、使学生产生共鸣感,有助于培养学生良好思想道德修养,对学生全面发展有很大帮助。本文结合现阶段高中数学教学实际情况,论述红色文化在高中数学教学中的运用。
【关键词】红色文化;高中数学教学;运用
红色文化是工农红军在中国共产党领导下,在战争和革命时期留下的宝贵物质及精神文化,若能将红色文化有效融入教学中则能使学生吸取其精华内容,有助于高中生良好人格的构建与各项优秀素养的形成,对学生发展有积极影响。现阶段部分教师仍存在对如何运用红色文化策略不足的问题,针对这种情况,教师应更好的挖掘红色文化并有效对之运用,响应党对现代教育的号召,不断提高自身教学水平。
1 创设红色文化教学情境
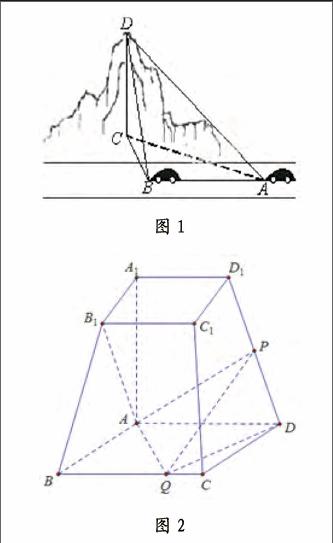
創设教学情境时教学的重要组成部分,是高效开展教学的前提条件,创设红色文化教学情境能使学生产生代入感,也能吸引学生学习兴趣,在活跃课堂氛围的同时使学生了解更多红色知识与红色文化。例如在教学《解三角形》一章时,对于其中正弦、余弦函数及其实用举例一部分,教师可以创设红色文化情境以引发学生思考,如“如图1所示,一辆汽车在遵义市娄山关一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=?”
运用遵义市娄山关一地区名称出题,将红色文化与教学情境有机结合,有助于吸引学生注意力,使其兴趣高涨。在出题的同时教师可以讲述在遵义市娄山关发生的革命时间,以在丰富学生知识储备的同时增强学生文化认同感,使红色文化深入学生内心。在提出问题时,教师不仅可以结合具体地名,也可以结合具体人名出题,并在同时为学生讲解与各人名、地名相关的历史故事,使学生在读题过程中获得丰富的情感体验。
2 开展红色文化专项练习
在讲解理论知识,巩固学生对基础知识掌握程度的同时,教师也应注重开展专项练习,提高学生对知识学以致用的能力,使学生解题能力得到提升。在开展专项练习时,教师可以将红色文化渗透入题干中,例如“已知遵义市中的习水市青杠坡历史英雄纪念碑处在台体上,如图2所示:已知四棱台ABCD—A1B1C1D1上下底面分别是边长为3和6的正方形,AA1=6,且AA1⊥底面ABCD,点P、Q分别在棱DD1、BC上。(1)若P是DD1的中点,证明AB1⊥PQ(2)若PQ∥平面ABB1A1,二面角P—QD—A的余弦值为3/7,求四面体ADPQ的体积”一题,将遵义市一具有红色气息的地名加入题干中,能将红色文化有效渗透到题目中,同时教师可以告诉学生:遵义会议是长征转折点,在遵义会议上做出的正确决策不仅挽救了工农红军,更挽救了中国共产党,而遵义市正是遵义会议的举办地。又如在教学二元一次不等式相关习题时,教师可以出题:“两名党内人士密谋在第二日早六点到七点间于码头碰面,已知两人坐不同的船前往码头,且两人到达时间不定,出于安全考虑两人船只只能在码头等对方十五分钟,求两人能碰面的概率为多少?”,以秘密会议为背景出题能在增强出题趣味性,激发学生解题兴趣的同时渗透红色文化。随后教师应具体讲解此题:假设两人到达码头的时间分别为x、y,则可列出不等式0≤x≤60、0≤y≤60,且由于两人均只能等对方十五分钟,故可以列出不等式x-15≤y≤x+15,再根据几何概型相关知识,算出不等式组所表达部分面积占总面积比例,最终得出两人碰面概率为7/16。
3 运用红色文化启发学生思维
数学是一门逻辑性极强的学科,在学生学习数学过程中其逻辑及思维能力都能得到很大提升,教师可以将红色文化与启发学生思维过程结合起来,使学生拥有更加迅捷的反应速度及缜密的思维,使学生不断受益。例如在教学排列组合相关知识时,教师可以结合具体问题以启发学生思维,如“瓮安县猴场会址的戏楼安装了5个彩灯,它们闪亮的顺序不固定.每个彩灯只能闪亮红、橙、黄、绿、蓝中的一种颜色,且这5个彩灯所闪亮的颜色各不相同,记这5个彩灯有序地各闪亮一次为一个闪烁.在每个闪烁中,每秒钟有且仅有一个彩灯闪亮,而相邻两个闪烁的时间间隔均为5秒.如果要实现所有不同的闪烁,那么需要的时间至少是( )A、1205秒 B、1200秒 C、1195秒 D、1190秒”并告诉学生解题思路:安装了五个彩灯即共有5*4*3*2*1=120次闪烁,共有119次间隔,教师应让学生联想彩灯闪烁的实际情况,使学生理解每个闪烁及每个间隔都需要用5秒,即共需要(119+120)*5=1195秒,此题应选C选项。也可以出题:“在中共某次会议结束后,参加会议所有成员决定合影留念,会议共有六名男性与一名女性,若要求两名女性不能站在队伍最左或最右边,那么共有多少种站法?”,给学生一定思考时间并随后为学生讲解:若不考虑特殊情况则共有7!=5040种站法,而当女性站在队伍靠边位置时,共有2*6!=1440种站法,故当女性不站在队伍靠边位置时,共有5040-1440=3600种站法。排列组合部分习题是高中数学难点,有效开展教学不仅能加强学生对此部分习题作答能力,更能使学生思维能力得到提升,有利于挖掘学生潜能。
4 结语
当代党的理念要求教育通过对红色文化的发掘,将红色文化中优秀理念运用至教学中以起到教书育人的作用,将红色文化与教学相结合以使学生更好地理解红色精神,培养学生不畏艰险、百折不挠的精神,同时使学生学习更加刻苦努力,使其成绩得到提升。本文结合现阶段高中数学教学实际情况,从创设红色文化教学情境、开展红色文化专项练习以及运用红色文化启发学生思维三个方面对在高中数学教学中如何运用红色文化进行论述。高中生学业任务繁重,往往缺少时间了解并学习红色文化及精神,而教师应紧密关注红色文化的发展并将其与教学有效联系起来,为建设红色文化做贡献。
参考文献
[1]管志雄.浅谈红色文化在高中教学中的挖掘和运用[J].农村经济与科技,2017,28(04):265-265.
[2]石世学.瓮安本土红色文化的教育价值再挖掘思路分析[J].考试周刊:教师版,2016(52):35-35.
作者单位
贵州省瓮安中学 贵州省瓮安县 550400endprint
