创设有效情境培养学生的数学建模能力

吴青

《义务教育数学课程标准（2011年版）》在课程设计思路中明确指出：“义務教育阶段数学课程的设计，充分考虑本阶段学生数学学习的特点……使学生体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程。”同时，将“模型思想”作为八个核心概念之一。由此可以看出，培养学生的数学建模能力，必须依托具体的生活情境，让学生充分感受生活情境，学会从复杂的生活情境中挑选有效信息，从而将生活问题抽象成数学问题，并综合运用所学数学知识进行解决。因此，在进行数学建模教学的过程中，生活情境的选择非常重要。我们要优选生活情境，使其具有一定的现实意义，并且要和儿童的实际生活密切联系，这样学生才容易理解其中隐含的问题，才能引起他们的探究欲望，从而将生活问题抽象成数学问题，并得到解决，实现数学建模。

一、创设有效的生活情境，将生活问题数学化

一切知识皆来源于生活，数学模型的构建更是依赖于一定的生活情境，只有在对生活情境有充分的了解，舍弃那些与问题无关的非本质因素，保留问题的本质因素之后，学生才能顺利地建立起有效的数学模型，从而将生活问题数学化。

说到数学建模，数学史上一个最著名的例子，就是格尼斯堡的七桥问题。当格尼斯堡的人们每天沿着市中心的7座桥散步时，不知不觉中便提出了一个问题：一个散步者能否一次走遍7座桥，而且每座桥只许通过一次，最后仍回到起始地点。这就是一个生活问题，然而在很长的一段时间内，人们都被河、桥、陆地这些因素所干扰，始终无法解决这个问题。而欧拉将陆地抽象成点，将桥抽象成线，舍弃了那些无关因素，从而将七桥问题转化成数学上的一笔画问题，进而顺利解决了这个困扰大家多年的问题。

从欧拉解决七桥问题的过程中，可以看出数学建模的魅力就在于能够将生活问题数学化，并运用数学知识来解决生活问题。因此在实际教学中，我们要善于从儿童的日常生活中选取可用的素材，创设丰富而有效的生活情境，让学生在情境中感悟、体验、思考、探究，进而将生活问题抽象成数学问题，从而得到解决。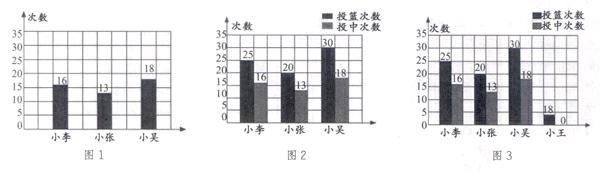

比如在教学和的奇偶性时，老师创设了一个抛骰子玩转盘的生活情境。抛骰子和玩转盘在学生的生活中很常见，由此拉近了学生与课堂探究内容之间的心理距离，也密切了数学与生活之间的联系。在这个游戏中规定，抛出骰子后，将抛到的数再加一遍，得到一个结果，然后在转盘上找到相应的数据，领取对应的奖品。学生玩了几次都是空手而返，这是为什么呢？在生动有趣的生活情境的渲染下，学生陷入了沉思中。很快有同学发现，转盘上奇数对应的都是奖品，而与偶数对应的则都是“谢谢参与”。还有学生意识到，将抛到的数再加一遍，不管原来抛到的是几，再加一遍之后都是偶数，因此都拿不到奖品。看来，拿不到奖品不是运气不好，而是规则定得不好。

于是，老师让学生修改规则，使得这个游戏更加公平。有学生提出，抛两次骰子，然后将两次抛到的数相加。那么，如何确定和的奇偶性呢？两个数相加，有哪几种不同的情形呢？接下来，学生分别研究偶数加偶数、奇数加奇数、偶数加奇数这三种不同情形下和的奇偶性，并最终得出规律。

在这个课例中，学生通过玩转盘这个具体的生活情境，将骰子和转盘这些无关因素舍弃，保留下来的则是两个数相加确定和的奇偶性，从而将生活问题抽象成数学问题，并建立起相应的数学模型。他们经历了生活问题数学化的过程，这是整个数学建模过程中最为关键的环节。

在六年级的一节数学活动课上，老师向学生介绍了古印度梵塔的传说。在古老传说的情境渲染下，再让学生玩汉诺塔，比一比谁的速度最快。当学生从2层汉诺塔开始，逐渐过渡到3层、4层、5层汉诺塔，难度逐渐加大，移动的次数也变得越来越多。于是有学生开始思考，在每一种情形下，最少需要移动的次数之间有怎样的规律。通过分析发现，n层汉诺塔最少需要移动2n-1次。在这个教学片段中，教师创设了梵塔传说与汉诺塔移动比赛的生活情境，学生在操作过程中，自主地将生活问题抽象成数学问题并建立起数学模型，思考最少移动次数存在的规律，进而解决了这个问题。

但是在这节课上，数学建模的过程并没有止于此，而是向着数学思维的纵深处发展。教师随后又创设了一个生活情境，向学生介绍了古印度的另一个传说，关于国际象棋发明者接受国王赏赐的故事：在棋盘的第1个小格里赏一粒麦子，在第2个小格里赏2粒，第3个小格赏4粒，以后每一小格都比前一小格加一倍，把棋盘上的64格都摆上麦粒。64格一共能摆放多少麦粒呢？学生纷纷拿起笔计算起来，真是不算不知道，一共竟然有264-1粒，这是一个20位数，真是一个超出我们感知能力的天文数字。

将刚才的两个例子进行对比，学生发现，两种不同的生活情境，两种不同的生活问题，最终都归结为2n-1这个统一的数学模型。同一个数学模型会应用到不同的生活问题中，会有不同的具体解释，所以数学模型具有高度的抽象性和概括性。

对小学数学而言，数学建模的过程，实际上就是生活问题数学化的过程，是学生在数学学习中获得某种带有模型意义的数学结构的过程。在这节课上，教师创设了两个不同的生活情境，让学生经历生活问题数学化的过程，当学生排除无关信息的干扰，把生活问题与一定的数学知识建立联系，把生活问题抽象为数学问题后，他们的数学思维能力也就得到了一次提升。而当学生认识到不同的生活问题竟然归结到同一个数学模型之中，他们对数学模型会有一个更深刻的认识，也为以后应用数学知识解决实际问题提供了丰富的数学经验。

二、创设优化的现实情境，将形象问题抽象化

我们在进行数学建模时，须要将生活问题进行一定的抽象，经过适当概括，提炼出抽象的数学模型。因此在课堂上，我们须要创设优化的现实情境，将生活问题形象地呈现出来，促使学生在直观的情境中分析、反思，并进一步进行抽象概括。endprint

数学模型的抽象化，主要是在数学概念方面运用得比较多，比如数的概念、几何概念等。由于这些概念本身就是对大量生活原型进行抽象概括之后得到的，所以在课堂教学中，我们要注重让学生在充分感知的基础上进行抽象概括。

比如在教学百分数的意义一课时，结合学校正在开展的篮球比赛，创设了评选最佳投篮运动员的现实情境，学生都来做小考官，对三位运动员的投篮情况进行评比。首先让学生分析图1给出的三位同学投中的次数，当有同学根据小吴投中次数最多，而选择小吴为最佳投篮运动员时，有同学提出反对意见，认为还应该考虑一共投篮的次数。这时出示图2，又有同学根据小张没有投中的个数最少，而选择小张。此时再出示图3，小王未投中的个数最少，是否小王投篮本领最好？在此基础上，学生进一步思考发现，可以计算出每位同学投中次数各占投篮总次数的几分之几，然后再进行比较。于是，百分数概念的得出就水到渠成了。

在这个教学片断中，教师选取了学生喜欢的、和他们生活密切相关的篮球比赛这一现实情境，学生在优化的情境中，感受生活问题并将其逐步抽象，从而得出百分数这一数学模型。

接下来和学生一起分析64%的含义，此时学生所能理解的还只是这个百分数的具体含义，还只是在投篮命中率这种生活情境之下的百分数。为了让学生更加充分地感受各种不同的百分数的情境，充分认识百分数的具体含义，并能抽象概括出百分数的一般意义，教师再一次创设了优化的现实情境，在班级开展“新闻发布会”，让学生都成为小小新闻发布员，向大家介绍自己收集的生活中的百分数，分析它们所表示的具体含义。通过对这些百分数具体含义的分析，学生对百分数这个数学概念有了更为深刻的认识，在此基础上进一步抽象，从而抽象概括出百分数的模型。

通过课堂上教师精心创设的两个优选的现实情境，学生在充分感受百分数具体实例的基础上，对生活中的百分数进行了深入思考，经过两次抽象概括，得出了百分数的数学模型。这不仅培养了他们的数学建模能力，也进一步发展了数学分析、概括和抽象能力。

三、创设模拟的操作情境，将具体问题一般化

数学知识源于生活，是对生活现象的抽象、概括与提升。许多生活现象之间都存在着数学上的某种联系，表现出相类似的规律性，可以将它们概括在一个更为普遍的数学模型之中。因此在数学课堂上，我们可以将现实生活中发生的与数学学习有关的素材引入课堂，让学生在教师精心创设的模拟情境中进行操作探究，将生活问题抽象成数学问题，并将具体问题一般化，从而得到一个更为普遍适用的数学模型，使学生体会到数学模型的高度概括性，认识到数学规律的普遍存在，从而对数学模型有更深的认识。

比如在教学格点与面积时，教师创设了一个师生比赛的生活情境，给出几个格点多边形，看谁能最先得到它的面积。几轮比赛都是老师获胜，学生在惊叹之余，非常想要找到计算格点多边形面积的秘密，于是开始研究内部格点数为1的这些格点多边形（这是老师给定的图形），从而发现它们的面积恰好等于边上格点数的一半，这是数学建模的开始。

可是，当学生画出内部格点数不是1的格点多边形时，却发现刚才的规律并不成立，看来刚才建立的数学模型只有在内部格点数为1时才成立，并不具有一般性，还是属于比较具体的情形，因此须要将它进行一般化，从而得到更为普遍适用的规律。于是，接下来再研究内部格点数为其他情形时的格点多边形，分别得出相应的规律，并最终将它们整合在一个统一的数学模型之中，将数学模型的构建推向最高点。

从上面的例子可以看出，通过教师精心创设的优化的生活情境，让学生从一个具体的生活问题出发，将其抽象成数学问题，研究它的解法，并上升到一种数学模型，最后再将其一般化，进行广泛的运用和推广，从而得到更为普遍的规律，建立起更具一般意义的数学模型。

在數学课堂上，我们要尽可能地创设有效的生活情境，帮助学生从生活问题中抽象出数学问题，建立数学模型，经历数学探究的过程，培养他们运用数学知识解决生活实际问题的能力，促使小学生的思维水平从直观形象思维向逻辑抽象思维过渡。

[责任编辑：陈国庆]endprint