负弯矩作用下半刚性钢管混凝土组合节点初始刚度计算

王冬花, 王静峰,2

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.安徽先进钢结构技术与产业化协同创新中心,安徽 合肥 230009)

负弯矩作用下半刚性钢管混凝土组合节点初始刚度计算

王冬花1, 王静峰1,2

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.安徽先进钢结构技术与产业化协同创新中心,安徽 合肥 230009)

“T形件”是组合结构梁柱连接节点的重要组件,文章利用组件法,以“T形件”为基本单元,分别给出了各组件的刚度计算方法,如钢筋抗拉刚度、柱壁抗压刚度、柱壁抗剪刚度、端板抗弯刚度、柱壁抗弯刚度、螺栓抗拉刚度,提出了负弯矩作用下端板连接半刚性钢管混凝土组合节点初始刚度计算公式;通过试验验证了所提负弯矩作用下组合节点初始刚度简化计算方法的正确性和准确性。该研究成果可为建立半刚性钢管混凝土组合框架设计方法提供科学依据。

组合节点;T形件;初始刚度;负弯矩;组件法

0 引 言

现有的设计和分析常假定梁柱连接为完全刚性连接(简称“刚接”)或理想铰接,然而实际工程中大多数连接是介于刚接和铰接之间的半刚性连接，因此,研究节点的半刚性对于实际工程应用具有非常重要的理论意义[1]。

节点连接的初始刚度是指弯矩作用下梁柱节点连接区处于弹性阶段时所具有的刚度。初始刚度是评价节点刚性的重要参数。端板连接半刚性钢管混凝土组合节点是指钢管混凝土柱和钢-混凝土组合梁通过端板和单边高强螺栓连接的组合节点,具有典型半刚性特性。该组合节点的初始刚度高于相同连接方式的钢节点。

国内外研究者对半刚性H型钢柱框架结构进行了相关试验,提出了组合节点的初始刚度简化计算方法。文献[2] 对半刚性连接钢框架进行了拟动力试验,得到了该结构的动力性能;文献[3] 通过试验研究了加劲对端板连接刚度的影响,得到了不同端板类型影响下的节点初始刚度;文献[4]获得了H型钢梁柱端板连接节点的初始刚度;文献[5-8]通过端板连接钢管混凝土组合节点试验得到了组合节点的初始刚度。欧洲规范EC3将梁柱节点分解为若干个“T形件”[9],文献[10-12]通过“T形件”研究确定柱壁、端板的撬力作用。对于钢管混凝土柱框架结构,可根据组件法将钢管混凝土柱简化为“T形件”。

本文利用组件法,选择“T形件”作为基本分析单元,考虑受拉钢筋、受压柱壁、受剪柱壁、受弯柱壁、受弯端板、受拉螺栓等对节点连接区初始刚度的影响,得到了负弯矩作用下端板连接半刚性钢管混凝土组合节点初始刚度的计算公式。

1 负弯矩作用下组合节点初始刚度

负弯矩作用下,处于弹性阶段的组合节点产生的整体变形δt可以由钢管柱壁的弯曲变形δcf、钢管柱壁受拉变形δcw,t、端板的弯曲变形δep、螺栓变形δbo等叠加而成,类似多个弹簧串并联,则组合节点整体变形δt为:

δt=δcw,t+δcf+δep+δbo

(1)

受拉组件的整体初始刚度与每个组件刚度之间的关系为:

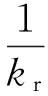
(2)

其中,kr为钢筋的抗拉刚度;kcw,t为钢管柱壁的抗压刚度;kcf为钢管柱壁的抗弯刚度;kep为端板的抗弯刚度;kbo为螺栓的抗拉刚度。负弯矩作用下的初始刚度计算模型如图1所示。

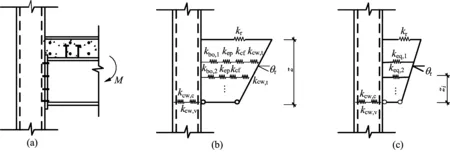
图1 负弯矩作用下组合节点初始刚度计算模型

当组件处于同一高度时,用一个等效的总刚度kep,i(i表示第i排)来表示这一高度各组件刚度;对于不同高度的组件,用一个等效力臂zeq,i来表示原来力臂z,通过替代,将各个组件位于同一高度,这时等效刚度kep,i为:

(3)

节点在负弯矩M作用下,由合力等效和弯矩等效可以建立如下方程:

(4)

其中,θr为节点连接的相对转角。

由(4)式可得:

(5)

在zeq处由于钢管柱壁受弯与受拉,螺栓受拉、端板受弯产生的总变形δt为:

δt=M/(zeqkeq)

(6)

钢管柱壁受压变形δc为:

δc=M/(zeqkcw,c)

(7)

其中,kcw,v为钢管柱壁的抗剪刚度。

两侧柱壁由于剪切变形而在zeq高度范围内产生的变形量δv为:

δv=M/(zeqkcw,v)

(8)

则θr为:

(9)

节点的初始刚度为:

(10)

2 负弯矩作用下各组件刚度确定

2.1 钢筋的抗拉刚度

负弯矩作用下,组合节点初始刚度应考虑混凝土楼板内纵向受力钢筋的抗拉刚度贡献。钢筋抗拉刚度kr为:

(11)

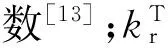
(12)

其中,Ar为钢筋的截面面积;E为钢管钢材的弹性模量;hc为钢管柱截面高度,圆柱取钢管外径。

kstud的计算公式为:

(13)

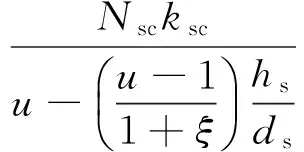
(14)

其中

Er为钢筋的弹性模量;Nsc为抗剪栓钉个数;ksc为栓钉的抗剪刚度;hs为钢筋中心至节点转动中心的距离;ds为钢筋中心至钢梁高度中心的距离;leff,b为负弯矩作用下,节点梁端计算长度,可取梁有效总长度的0.15[13];Eb为钢梁的弹性模量;Ib为钢梁截面惯性矩。

2.2 钢管柱壁的抗压刚度

负弯矩作用下,组合节点应考虑钢管柱壁的受压变形,计算中可用承受均布荷载两对边固定支撑的矩形板来简化钢管柱壁,如图2所示。由弹性力学理论可知,钢梁受压翼缘压力Fc,bf通过端板传递给钢管柱壁,其变形δcw,c为:

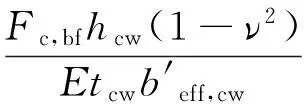
(15)

钢管柱壁的抗压刚度为:

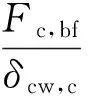
(16)

(17)

其中,tbf为梁翼缘厚度;tcf为钢管柱壁厚度;tep为连接端板厚度;hf,ep为端板与钢梁连接焊缝有效高度。

图2 钢管柱壁受压计算模型

2.3 钢管柱壁的抗剪刚度

剪力作用下钢管柱壁的变形δcw,v如图3所示,计算δcw,v时,假定侧向钢管柱壁为一个剪力作用下的短柱[15]。对于该短柱,此时受弯变形要远小于受剪变形,可忽略钢管柱壁弯曲变形。

图3 柱壁的剪切变形

δcw,v计算公式为:

(18)

Av,cw=(hcw-2tcw)tcw

(19)

(18)式可进一步表达为:

(20)

取受剪钢管柱壁为研究对象,左、右两侧承受的弯矩分别为M1和M2,如图4所示,则钢管柱壁上所受剪力V为:

V=(M1+M2)/zcw,v

(21)

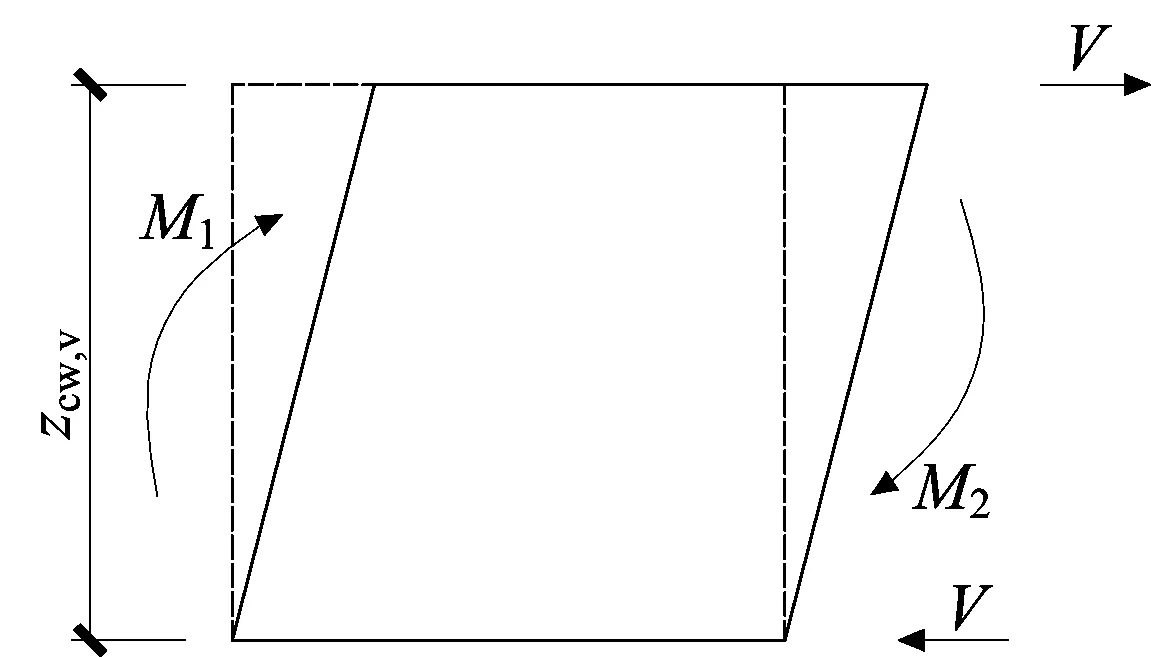
图4 受剪钢管柱壁剪切区域计算模型

钢梁翼缘拉力Ft,bf与受剪钢管柱壁所受的剪力V关系[18]为:

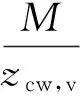
(22)

其中,M为组合节点承受的弯矩;β为与节点受剪边数相关参数,且β≤2,计算公式为:

(23)

对于边柱节点,取β=1;对于中柱节点,按以下规则计算:

(1) 组合节点承受对称弯矩时,取β=0,即kcw,v=∞。

(2) 组合节点承受大小相等、方向相同弯矩时,取β=2。

(3) 其他情形按(23)式计算。

受剪钢管柱壁的抗剪刚度为:

(24)

2.4 钢管柱壁和端板的抗弯刚度

2.4.1T形连接件简化模型

T形连接件的简化模型如图5所示,“T形件”在拉力作用下的受力和变形如图5a所示。为了计算“T形件”底部受撬力作用产生的变形δT,将两端钢梁受力翼缘等效为简支梁支座,简支梁受拉力2FT作用,如图5b所示。δT的简化计算公式为:

(25)

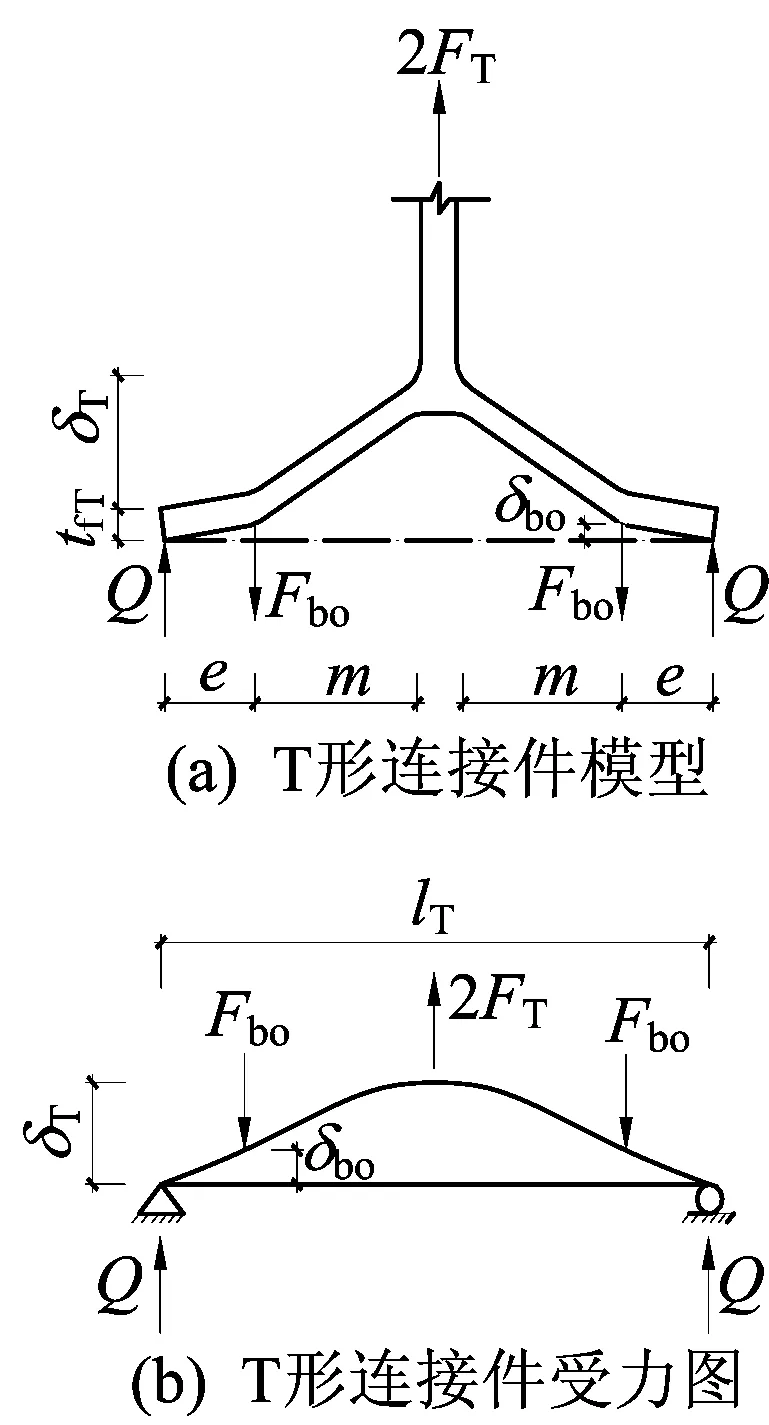
图5 T形连接件的简化模型

2.4.2 钢管柱壁和端板的抗弯刚度

通过“T形件”简化模型可知,在2FT拉力作用下,钢管柱壁会弯曲变形,此时钢管柱壁和端板的变形分别为:

(26)

(27)

其中

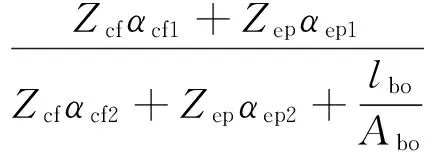
αcf=ec/lcf;αep=ee/lep;

Ecf为钢管柱壁弹性模量;Eep为端板弹性模量;lcf为将柱壁对应的T形连接件简化为简支梁计算模型的梁计算跨度;ec为螺栓中心至柱翼缘边缘的距离;mc为螺栓中心至柱腹板边缘的距离;Icf为柱壁简化模型的抗弯模量;lep为端板对应的T形连接件简化为简支梁计算模型的梁计算跨度;ee为螺栓中心至梁翼缘边缘的距离;me为螺栓中心至梁腹板边缘的距离;Iep为端板简化模型的抗弯模量。

柱壁与端板的抗弯刚度kcf、kep为:

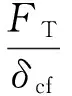
(28)

(29)

在计算柱壁与端板的变形和抗弯刚度时还应充分考虑螺栓对钢管柱壁撬力影响。但在实际工程中,考虑撬力极为复杂繁琐,为了简化计算,忽略部分螺栓撬力的影响,则钢管柱壁和端板的变形分别为:

(30)

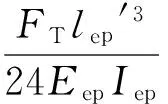
(31)

其中,lcf′、lep′分别为不考虑受拉螺栓撬力影响时对应简化模型的钢管柱壁和端板计算宽度,lcf′=2mc，lep′=2me。此时钢管柱壁与端板的抗弯刚度为:

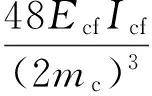
(32)

(33)

其中,leff,cf为钢管柱计算宽度;leff,ep为端板计算宽度。

研究表明,采用高强螺栓连接时,高强螺栓预紧力改变了“T形件”翼缘板简化模型计算跨度和其边界约束条件,这将改变整个“T形件”受力性能和变形机理,因此在计算组合节点的初始刚度时,应考虑高强螺栓预紧力的影响。考虑高强螺栓的预紧力,“T形件”受拉变形会在预紧力的作用下减小。在分析变形时假定翼缘板的两端为固定支座,假定拉力作用在“T形件”跨中,如图6所示,梁模型计算跨度lT′取2m。

图6 考虑高强螺栓预紧力影响时的T形连接件计算模型

计算中忽略螺栓栓帽、撬力、垫圈等因素的影响,将螺栓的伸长量δbo作为支座的刚体位移,“T形件”翼缘板的变形δT为:

(34)

其中,tp为高强度螺栓连接的板厚度;Abo为螺栓的有效抗拉面积;Ebo为螺栓弹性模量。

则考虑高强度螺栓预紧力影响的“T形件”的转动刚度为:

(35)

此时钢管柱壁和端板的抗弯刚度分别为:

(36)

(37)

其中,Fcf为作用在钢管柱壁上的外荷载;Fep为作用在端板上的外荷载。

2.5 螺栓的抗拉刚度

计算中还应考虑螺栓自身的影响,按照EC3规范[9],螺栓抗拉刚度kbo为:

(38)

其中,lbo为螺栓的计算长度。若考虑高强螺栓的预紧力影响,此时螺栓抗拉刚度为:

(39)

其中,λ为考虑高强螺栓的预紧力影响系数。

3 试验验证

将本文计算结果与文献[1]中4榀足尺端板连接钢管混凝土组合节点试验结果进行对比。负弯矩作用下，组合节点的初始刚度计算值Ki,c与试验值Ki,t的对比结果见表1所列。

表1 计算值与试验值的比较

从表1可知,Ki,c/Ki,t的均值为0.912,方差为0.000 599,试验值比计算值大6%～13%,计算较为保守。

4 结 论

本文选择“T形件”作为分析基本单元,分别得到了钢筋抗拉刚度、柱壁抗压刚度、端板抗弯刚度、柱壁抗剪刚度、螺栓抗拉刚度、柱壁抗弯刚度。利用组件法,对组合节点初始刚度产生贡献组件进行组合,得到了负弯矩作用下半刚性钢管混凝土组合节点的初始刚度计算公式，与试验结果相比,计算结果较为保守。该研究成果可为建立半刚性钢管混凝土组合框架设计方法提供科学依据。

[1] 姜涛.半刚性钢管混凝土组合框架节点的抗震性能及设计方法[D].合肥:合肥工业大学,2012.

[2] 完海鹰,郑晓清.半刚性连接整体钢框架拟动力试验分析[J].合肥工业大学学报(自然科学版),2008,31(12):2013-2015.

[3] 王素芳,陈以一.加强式端板连接节点的初始刚度与抗弯承载力[J].东南大学学报(自然科学版),2008,38(5):774-778.

[4] 王海涛.端板型半刚性钢管混凝土框架的抗震性能及连续倒塌研究[D].合肥:合肥工业大学,2015.

[5] LOH H Y,UY B,BRADFORD M A.The effects of partial shear connection in the hogging moment regions of composite beams:part I:experimental study[J].Journal of Constructional Steel Research,2004,60(6):897-919.

[6] LOH H Y,UY B,BRADFORD M A.The effects of partial shear connection in the hogging moment regions of composite beams:part II:analytical study[J].Journal of Constructional Steel Research,2004,60(6):921-962.

[7] MIRZA O,UY B.Behaviour of composite beam-column flush end-plate connections subjected to low-probability,high-consequence loading[J].Engineering Structures,2011,33(2):647-662.

[8] 王静峰,潘学蓓,彭啸,等.两层钢管混凝土柱与组合梁单边螺栓端板连接框架拟动力试验研究[J].土木工程学报,2016,49(10):32-40.

[9] Eurocode3:design of steel structures:part 1.8:design of joints[S].Brussels:European Committee for Standardization,2005:162-164.

[10] NEMATI N,HOUEDEC D L,ZANDONINI R.Numerical modelling of the cyclic behaviour of the basic components of steel end plate connections[J].Advances in Engineering Software,2000,31(11):837-849.

[11] SWANDON J A,LEON R T.Stiffness modeling of bolted T-stub connection components[J].Journal of Structural Engineering,2001,127 (5):498-505.

[12] BURSI O S,FERRARIO F,FONTANARI V.Non-linear analysis of the low-cycle fracture behaviour of isolated Tee stub connections[J].Computers and Structures,2002,80(S27/S28/S29/S30):2333-2360.

[13] GRUNDY P,THOMAS I R,BENNETTS I D.Beam-to-column moment connections[J].Journal of the Structural Division,1980,106(1):313-330.

[14] ACKROYD M.Design of flexibility-connected unbraced steel building frames[J].Journal of Constructional Steel Research,1987,8(7):261-286.

[15] YEE L,MELCHERS R E.Moment-rotation curves for bolted connections[J].Journal of Structural Engineering,1986,112(3):615-635.

[16] FRYE M J,MORRIS G A.Analysis of flexibly connected steel frames [J].Canadian Journal of Civil Engineering,1976,2(2):280-291.

[17] JOHNSON R P,ANDERSON D.EN1994 Eurocode 4:design of composite steel and concrete structures[J].Civil Engineering,2001,144(6):33-38.

[18] KISH N,CHEN W F.Moment-rotation relations of semi-rigid connections with angles[J].Journal of Structural Engineering,1990,116(7):1813-1834.

Calculationofinitialstiffnessofsemi-rigidCFSTcompositejointssubjectedtonegativemoment

WANG Donghua1, WANG Jingfeng1,2

(1.School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China; 2.Anhui Advanced Steel Structural Technology and Industrialization Collaborative Innovation Center, Hefei 230009, China)

T-shaped component is an important component of beam-to-column connection of the composite structure. Selecting T-shaped component as basic element and using the component method, the calculation method of initial stiffness of semi-rigid concrete-filled steel tubular(CFST) composite joints under negative moment is obtained. Some components are given, including reinforced bar tensile stiffness, column wall compressive stiffness, column wall anti-shear stiffness, end plate bending stiffness, column wall bending stiffness and bolt tensile stiffness. The correctness and accuracy of the simplified calculation method of initial stiffness of semi-rigid CFST composite joints under negative moment are verified by experiments. The research results can provide a scientific basis for the design of semi-rigid CFST composite frame.

composite joint； T-shaped component; initial stiffness; negative moment; component method

2016-03-01；

2016-05-03

国家自然科学基金资助项目(51178156);教育部新世纪优秀人才支持计划资助项目(NCET-12-0838)

王冬花(1984-),女,安徽巢湖人,合肥工业大学博士生;

王静峰(1976-),男,安徽合肥人,博士,合肥工业大学教授,博士生导师,通讯作者,E-mail:jfwang008@163.com.

10.3969/j.issn.1003-5060.2017.09.016

TU311.4

A

1003-5060(2017)09-1231-06

(责任编辑 张淑艳)