考虑作业释放时间和机器数量变化的同型机调度问题
2017-10-24赵福强刘桂庆
赵福强, 刘桂庆
(合肥工业大学 数学学院,安徽 合肥 230009)
考虑作业释放时间和机器数量变化的同型机调度问题
赵福强, 刘桂庆
(合肥工业大学 数学学院,安徽 合肥 230009)
同型机调度;机器影响;释放时间;可中断;最大完工时间
0 引 言
生产调度问题是一类典型的组合优化问题,它旨在利用现有资源,在满足一些必要条件基础上完成一定任务并达到特定的调度目标。在现代生产制造中,企业投入生产的机器数量是制造加工系统的一个重要特征,因此研究机器数量投入对企业生产效率的影响具有重要意义。当企业接收一批订单后,虽然有足够的机器资源去加工这些订单,但如果投入很多机器处理这些订单,很可能造成资源浪费。另外,机器数量变化调度问题不同于传统调度问题。因此,该项研究内容具有重要的理论价值和现实意义。
关于作业带有释放时间且允许中断的2台同型机的最小化完工时间和问题,文献[6]提出了一个启发式算法,并证明了某些特殊的实例,该算法能够得到最优调度,指出了当有n个作业时该算法的最坏情况误差界为2(1-1/n)。关于作业带有释放时间且允许中断m个同型机的最小化最大完工时间问题,文献[7]构造了改进的McNaughton规则,并证明该规则可以求出该问题的最优解。另外,有些学者研究了考虑释放时间其他目标函数的平行机调度问题。例如,文献[8]基于SPT和ERD规则的综合改进,为作业带有释放时间单机最小化完工时间和问题提出一种INSERT算法,并运用大量实验数据证明了其性能更优。关于作业带有释放时间的m个同型机的最小化完工时间和问题,文献[9]将此问题松弛成可中断的问题加以解决,再将松弛问题的解可行化,提出了一个竞争比为7/3的近似算法;文献[10]运用作业分割技术为此问题建立下界,进而构造分枝定界算法,能够解决2台机器100个作业规模的问题。
1 问题描述
本文研究的问题基于以下几点假设:
(1) 机器的生产能力有限,机器在工作时间一直处于启动状态,且不考虑设备故障。
(2) 每个作业在任一台机器上的加工顺序都有且只有一个,每台机器任一时刻只能加工一个作业,任一作业同一时刻只能被一台机器加工,机器在没有安排作业或作业没有到达时是空闲的。
(3) 不考虑原材料短缺和操作人员空缺的情况。
本文研究问题描述如下:有n个作业J={Jj|j=1,2,…,n;n≥m}在m台机器M={Mi|i=1,2,…,m;m≥2}上加工(不妨设每台机器的速度为单位速度),每个作业有释放时间rj(rj≥0),加工时间pj(pj>0),各作业之间相互独立。每个作业要在释放时间后才能被加工,加工过程可以中断,作业在任何时间都可以被中断,也可以在任何时间继续加工且中断后再加工时不接受惩罚,目标是最优化机器影响,具体可表示为:
(1)
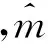

2 问题分析及算法设计
2.1 问题分析
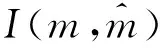
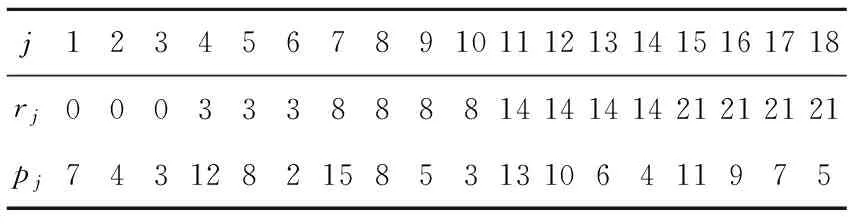
基于以上解决思路,本文将作业按释放时间单调不减的顺序排列,即r1≤r2≤…≤rn。设rj(j=1,2,…,n)中有k个不同的数,记为r1=t1 2.2 算法P (1) 若将Ti中的作业按加工时间单调不增排序得到新的作业集Si,设ni为Si中作业的个数,即|Si|=ni,则Si中的作业加工时间满足pi1≥pi2≥…≥pini。当i=1,2,…,k-1,若存在xi(1≤xi (2) 若xi≥m,则将Si中前m个作业按顺序排在m台机器上加工,此时对应的作业调度即为区间[ti,ti+1](i=1,2,…,k-1)上作业在m台机器上的调度。令pil=pil-li(l=1,2,…,m),Ti+1=Ti+1∪{pi1,pi2,…,pim,…,pini},i=i+1,转步骤(1)。若xi (5) 令Ti+1=Ti+1∪{pini},Ti=Ti-{pini},转步骤(1)。 步骤(2)保证当前可以在加工作业集Ti中大于或等于区间长度的作业,超出区间长度的那部分作业中断,放到下一个区间加工。如果机器还有空闲,步骤(3)~步骤(5)讨论如何加工Ti中其余作业。 证明由题设条件可知: 则在区间[ti,ti+1](i=1,2,…,k-1)上, 引理1 对问题Pm|rj,pmtn|Cmax,若一个可行调度Sp满足如下条件: (1) 在调度Sp中的每一个区间[t1,t2],[t2,t3],…,[tk-1,tk]上机器无空闲,或当前区间可以加工的作业已经加工完成。 (2) 在调度Sp中的最后一个区间[tk,tk+1)上,最大加工时间pk1具有如下性质之一:①pk1的准备时间为tk,即此作业在前k-1个区间都不能被加工;②pk1是被中断后的剩余加工时间,而且从它的释放时间开始就一直被加工。 (3) 在调度Sp中的最后一个区间[tk,tk+1)上,设还没加工作业的时间为pk1,pk2,…,pknk,此调度下得到的时间表长为Cmax(Sp),且有: 则同时具备以上3个条件的调度Sp为最优调度。 由条件(2)知,加工时间pk1被中断的可能性最小。 故同时具备以上3个条件的调度为问题Pm|rj,pmtn|Cmax的最优调度。证毕。 证明设算法P得到的调度结果是S*。根据算法P的步骤可以看出,调度S*具备引理的是3个条件,因此调度S*为最优调度。证毕。 表1 作业信息 在区间[3,8]上,T2={12,8,2}∪{4,1}∪{3},S2={12,8,4,3,2,1},l2=5。依次将前2个作业安排在2台机器上加工,超过区间范围的就此中断,则中断剩余的作业时间为{7,3},余下的作业时间为{4,3,2,1},此区间机器被排满。 在区间[8,14]上,T3={15,8,5,3}∪{4,3,2,1}∪{7,3},S3={15,8,7,5,4,3,3,3,2,1},l3=6。依次将前2个作业安排在2台机器上加工,超过区间范围的就此中断,则中断剩余的作业时间为{9,2},余下的作业时间为{7,5,4,3,3,3,2,1},此区间机器被排满。 在区间[14,21]上,T4={13,10,6,4}∪{9,2}∪{7,5,4,3,3,3,2,1},S4={13,10,9,7,6,5,4,4,3,3,3,2,2,1},l4=7。依次将前2个作业安排在2台机器上加工,超过区间范围的就此中断,则中断剩余的作业时间为{6,3},余下的作业时间为{9,7,6,5,4,4,3,3,3,2,2,1},此区间机器被排满。 I(2,2)=66/66=1。 作业最优调度方案如下: 具体如图1所示。 图时,作业最优调度的Gantt chart 具体如图2所示。 图时,作业最优调度的Gantt chart 具体如图3所示。 图时,作业最优调度的Gantt chart 具体如图4所示。 图时,作业最优调度的Gantt chart 图5 机器影响随机器数量变化曲线 本文作业加工过程是可中断的,当作业中断后恢复再加工,是否接受一定的惩罚是企业制造需要考虑的问题;对于作业不可中断情形,也有待进一步的讨论。考虑到机器环境情况,对应的同类机调度问题也是值得研究的课题。 [1] BREHOB M,TORNG E,UTHAISOMBUT P.Applying extra-resource analysis to load balancing[J].Journal of Scheduling,2000,3(5):273-288. [2] GRAHAM R L.Bounds for certain multiprocessing anomalies[J].Bell System Technical Journal,1966,45(9):1563-1581. [3] CHEN B,VAN VLIET A,WOEGINGER G.An optimal algorithm for preemptive on-line scheduling[J].Operations Research Letters,1995,18(3):127-131. [4] RUSTOGI K,STRUSEVICH V A.Parallel machine scheduling:impact of adding extra machines[J].Operations Research,2013,61(5):1243-1257. [5] 鲁习文.同型平行机上在线排序问题的近似算法[J].运筹与管理,2004,13(6):11-15,95. [6] 程贞敏,张喜娟,李洪兴.工件带准备时间的平行机调度问题的一个近似算法[J].北京师范大学学报(自然科学版),2009,45(4):350-354. [7] HONG K S,LEUNG J Y T.On-line scheduling of real-time tasks[J].IEEE Transactions on Computers,1992,41(10):1326-1331. [8] 李凯,马华伟,杨善林.含作业到达时间的单机调度问题的改进算法[J].中国机械工程,2008,19(8):929-932. [9] PHILLIPS C A,SCHULZ A S,SHMOYS D B,et al.Improved bounds on relaxations of a parallel machinescheduling problem[J].Journal of Combinatorial Optimization,1998,1(4):413-426. [10] YALAOUI F,CHU C.New exact method to solve thePm|rj|∑Cjschedule problem[J].International Journal of Production Economics,2006,100(1):168-179. Identicalparallelmachineschedulingproblemwithreleasedatesandthechangeofthenumberofmachines ZHAO Fuqiang, LIU Guiqing (School of Mathematics, Hefei University of Technology, Hefei 230009, China) identical parallel machine scheduling; machine impact; release date; preemptive; makespan 2016-04-21; 2016-08-17 教育部高等学校博士学科点专项科研基金资助项目(20120111120013) 赵福强(1989-),男,安徽阜阳人,合肥工业大学硕士生; 刘桂庆(1978-),女,安徽和县人,博士,合肥工业大学副教授,硕士生导师,通讯作者:E-mail:769450363@qq.com. 10.3969/j.issn.1003-5060.2017.09.025 O223 A 1003-5060(2017)09-1283-06 (责任编辑 万伦来)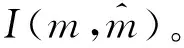

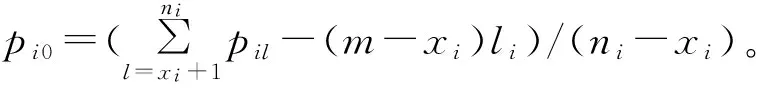
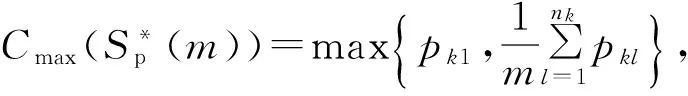
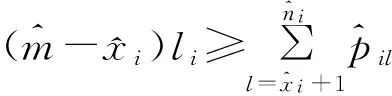
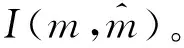


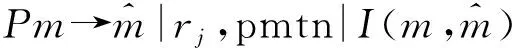
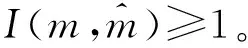
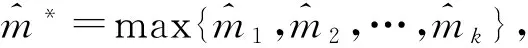

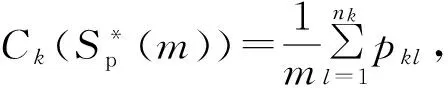
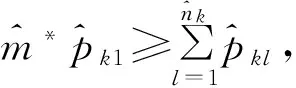
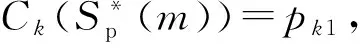

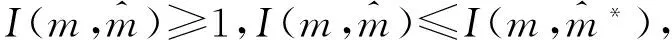
3 算 例
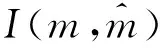


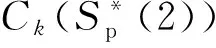
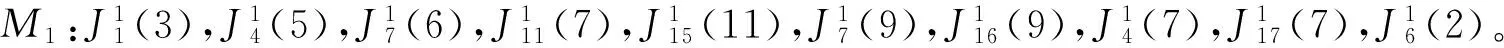


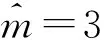
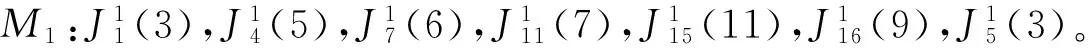
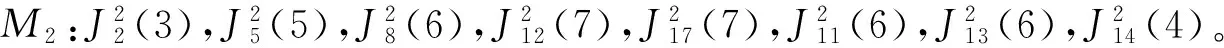

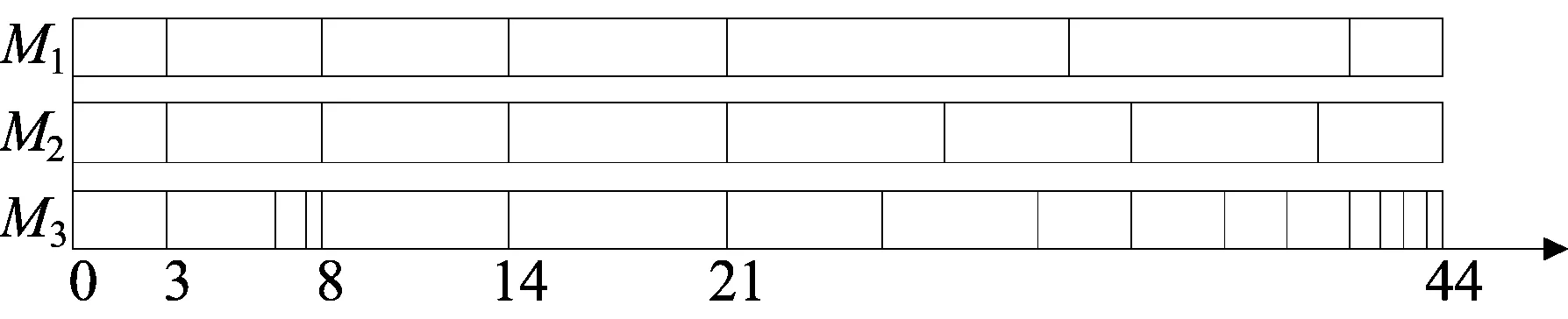
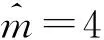
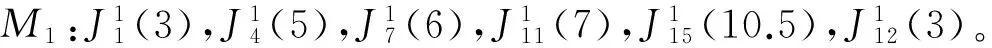
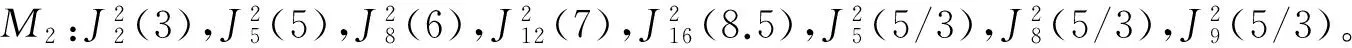

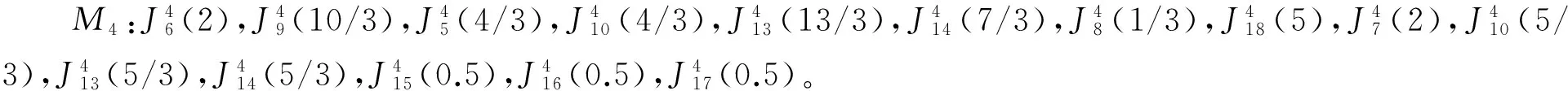

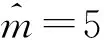
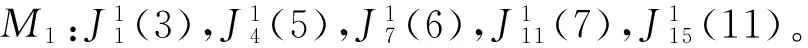
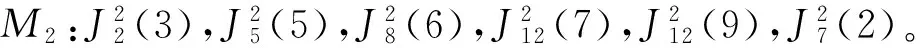

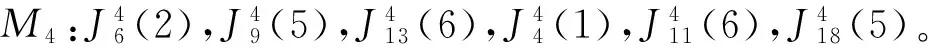


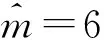
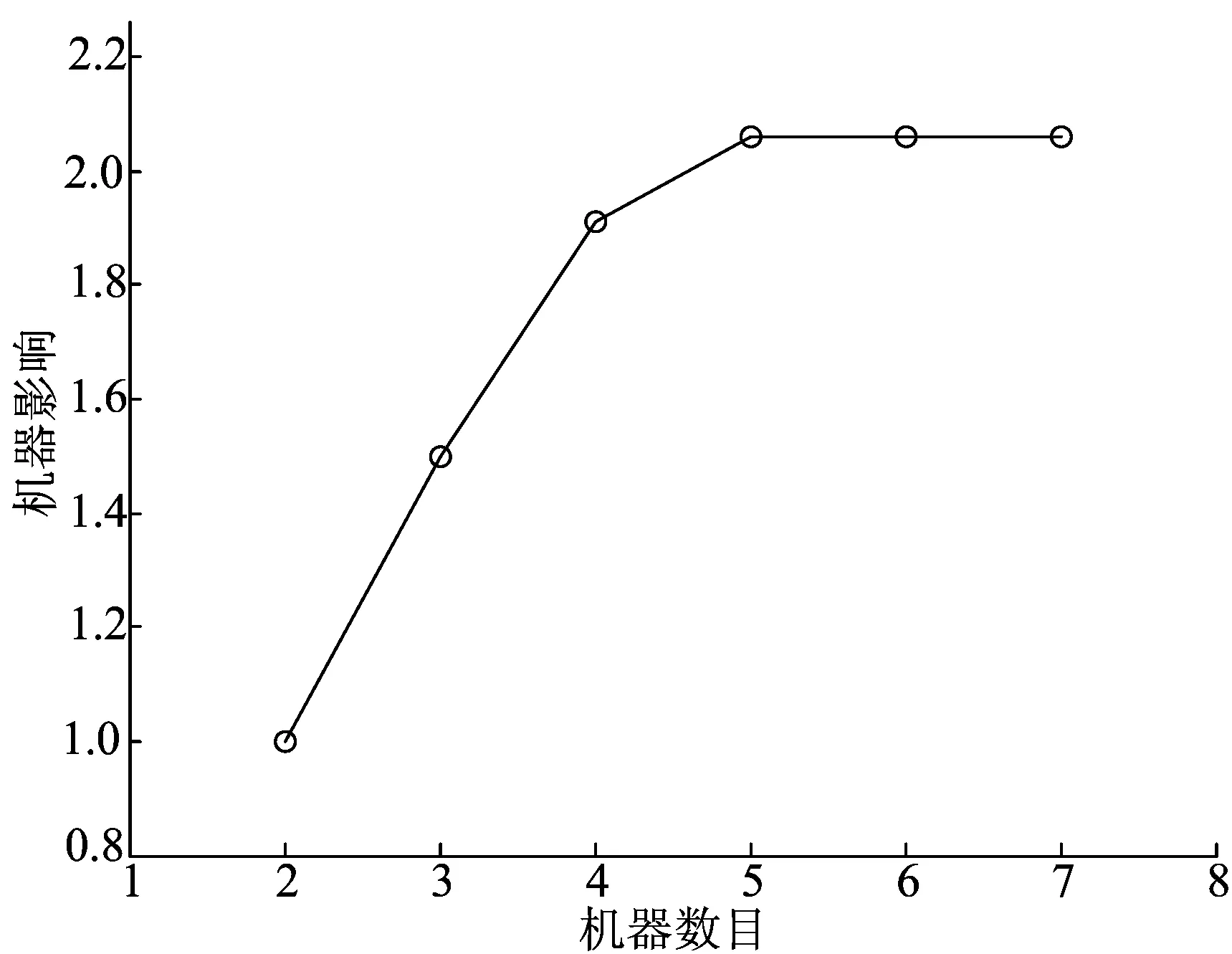

4 结 论