基于三次样条插值法的滑坡变形阶段分析
2017-10-24黄小研贾培刚
黄小研,贾培刚
(西安工业大学机电工程学院,陕西 西安 710021)
基于三次样条插值法的滑坡变形阶段分析
黄小研,贾培刚
(西安工业大学机电工程学院,陕西 西安 710021)
滑坡位移监测数据能够有效、直接地反映出滑坡整体变形趋势,在监测过程中,由于受到干扰或遇到设备故障,常会导致数据异常或缺失。基于三次样条插值法,对某新建工程监测位移的缺失数据进行了插值,使用t检验法对插值后的数据进行了显著性检验,并利用切线角法对插值后的累计位移数据进行了变形阶段分析。结果表明,利用三次样条插值法得到的插值数据与原始数据没有显著差异,滑坡处于加速变形阶段,可进行短期预报。
三次样条插值;t检验法;切线角法;滑坡变形阶段
采集滑坡位移数据时,自动化监测设备会受到外界影响而产生异常值,或因设备故障而缺失部分数据。如果直接采用原始位移数据分析滑坡变形阶段,或预测后续滑坡变形趋势,则会出现与实际值偏差过大的情况。因此,在分析滑坡变形前,需对得到的原始位移数据进行预处理。对于原始位移数据的缺失一般采用插值方法,插值法是一种重要的数学计算工具,在诸多领域都有应用,包括线性插值法、拉格朗日(Lagrange)插值法、牛顿(Newton)插值法、分段插值法和样条插值法等,其中,样条插值法是在每两个相邻节点构成的一个小区间内用一个低次多项式来逼近,并保证在各个节点处的连接是光滑的。经过三次样条插值法处理的插值数据曲线变得光滑,如果与原始数据差异不显著,便可使用切线角法进行滑坡变形阶段分析。分析时,应使用累计位移数据,并构造累计位移—时间曲线。从曲线的大致趋势可先简单判断滑坡位移趋势,之后再根据切线角法计算各个小区间的曲线斜率,通过变形速率便可判断滑坡变形阶段。
1 三次样条插值法基本原理及显著性检验
1.1 三次样条插值法
考虑到高次插值不收敛又不稳定,而二次插值拟合的函数光滑性不够,所以,选择三次样条插值法对滑坡数据进行插值。三次样条插值函数的基本定义为:如果函数f(x)在节点x0,x1,…,xn处的函数值为 f(xi)=yi,i=0,1,…,n,并且关于这个节点集的三次样条函数S(x)满足插值条件S(xi)=yi,i=0,1,…,n,则称这个三次样条函数S(x)为三次样条插值函数。
在每个小区间[xi,xi+1]上,三次样条函数可以表示为:

式(1)中:hi为步长,满足 hi=xi+1-xi,i=1,2,…,n-1.
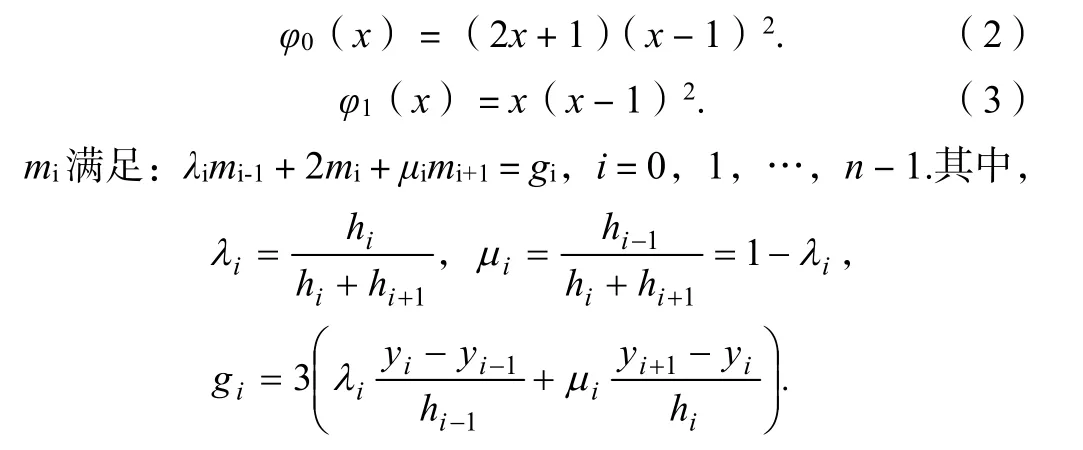
本文中,边界条件满足自然边界条件,即S"(x1)=M1,S"(xn)=Mn,由此可得,M1=Mn=0.所以有:

联合基本方程组可得到mi矩阵:

将求得的各未知数代入式(1)就可得到三次样条函数的表达式。
1.2 t检验
t检验是用t分布理论来推论差异发生的概率,从而比较2个平均数的差异是否显著。本文选取单总体t检验对插值前后的数据进行比较。如果总体标准差σ未知且样本容量n<30,那么,样本平均数与总体平均数的离差统计量呈t分布。此时,检验统计量为:

如果样本总数为大样本(n>30),检验统计量也可写为:

式(5)(6)中:X为样本平均数;μ为总体平均数;σX为样本标准差;n为样本容量。
计算自由度df=n-1,选定显著性水平,查询t检验表,如果t<t0.05(df),则接受原假设,即认为插值前后的数据差别不显著;反之,则拒绝原假设,认为插值前后数据差别过大,不适用于后期的滑坡变形阶段分析。
2 滑坡变形阶段分析
原始数据经过三次样条插值处理、t检验可靠之后,即可进行滑坡变形阶段分析,一般常采用切线角法。切线角的线性拟合方程为:
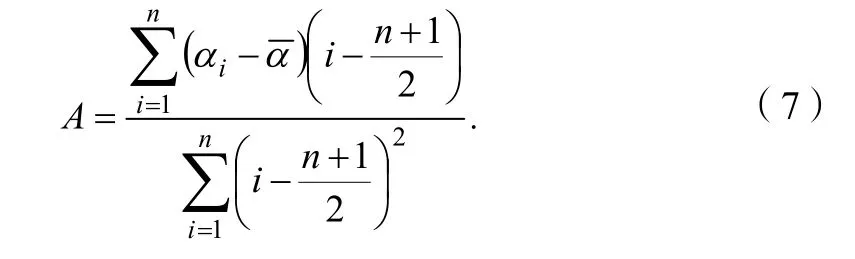
式(7)中:A为方程的斜率值。
式(7)适用于监测值为等时间间隔数据,如果时间间隔不等,可使用式(8),即:

式(8)中:i=1,2,…,n,为时间序号;ti为累计监测时间;t为时间ti的平均值;αi为xi处的切线角;α为切线角αi的平均值。
αi的计算公式为:
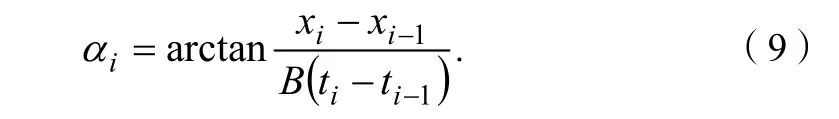
式(9)中:B为比例尺度。
比例尺度的计算公式是:
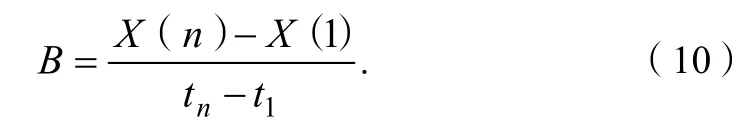
根据求得的A,B值,查询表1即可判别滑坡变形阶段。
如果滑坡位移监测数据量较大,可分段分析数据。如果划分为n(n=1,2,…,n)段,则分别对是对整体数据的分析。
3 滑坡变形阶段分析实例
3.1 三次样条插值法
为了便于分析,本文选取了某新建工程一个月的滑坡监测数据作为原始数据列,其具体数据如表2所示。
计算时,横坐标参数为日期,无法计算,所以,将所有横坐标均换成可计算的数字,如果遇到确实点,便多空过去一个数字。由于计算过程复杂,数据量多,本文所有参数均使用MATLAB编程算出。根据式(1)(2)(3),λimi-1+2mi+μimi=gi,i=0,1,…,n-1,S"(x1)=M1,S"(xn)=式(4)经过计算后可以得到全部三次样条插值方程。此处截取了缺失数据点前后两点构成的小区间所计算出的函数方程组,对其余方程组进行了省略,部分函数如下:

通过上述方程组各缺失点对应的函数可计算出相应的缺失值,如表3所示。在图1中,折线表示原始位移数据,曲线表示插值位移数据,圆圈表示各缺失点对用的缺失值。

图1 原始位移数据曲线与插值曲线对比
从图1中可以看出,三次样条插值法保证了每个小区间在连接点处的连续性,除去数据缺失点,原始数据曲线与插值曲线之间有许多基本重合的地方。由此可见,三次样条插值法具有较好的收敛性。
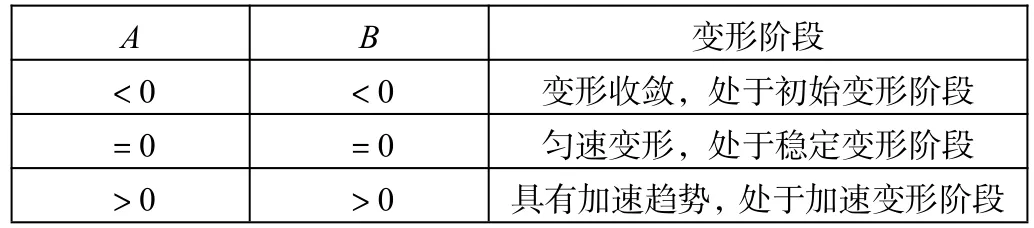
表1 滑坡切线角法变形阶段分析表

表2 滑坡监测位移原始数据表

表3 各缺失点对应的缺失值
3.2 检验
根据数据表2中的原始位移数据可计算出其平均数为2.688 8,标准差为0.672 1;插值后插值点样本数n=5,样本平均数X=2.482 1.建立原假设检验H0∶μ=2.666 8,认为插值后数据与原始数据之间的差别不显著。由于样本数小于30,根据公式(5)可计算出:

选取显著性水平为0.05,自由度df=4,查询t值临界表,临界值t0.05(4)=2.776.由此可见,样本的t值远远小于临界值2.776.因此,接受原假设检验H0,认为插值前后数据差别不显著,可进行滑坡变形阶段的分析。
3.3 变形阶段分析
根据上述分析,插值后的缺失值具有显著性,可进行滑坡变形阶段的分析。将原始位移数据与插值位移数据相结合,构成新数据列进行数据累加,使其成为累计位移数据列,并绘制出累计位移—时间曲线图,如图2所示。

图2 插值后累计位移数据
从图2中可以简单看出滑坡的整体变形趋势,但仅仅通过图像去判断变形趋势过于片面,因此,我们依据切线角法对此数据列进行相关参数计算。根据式(10)先计算出参数B,再根据式(1)和式(7)计算出参数A,并根据表1判断该滑坡的变形阶段,分析结果如表4所示。
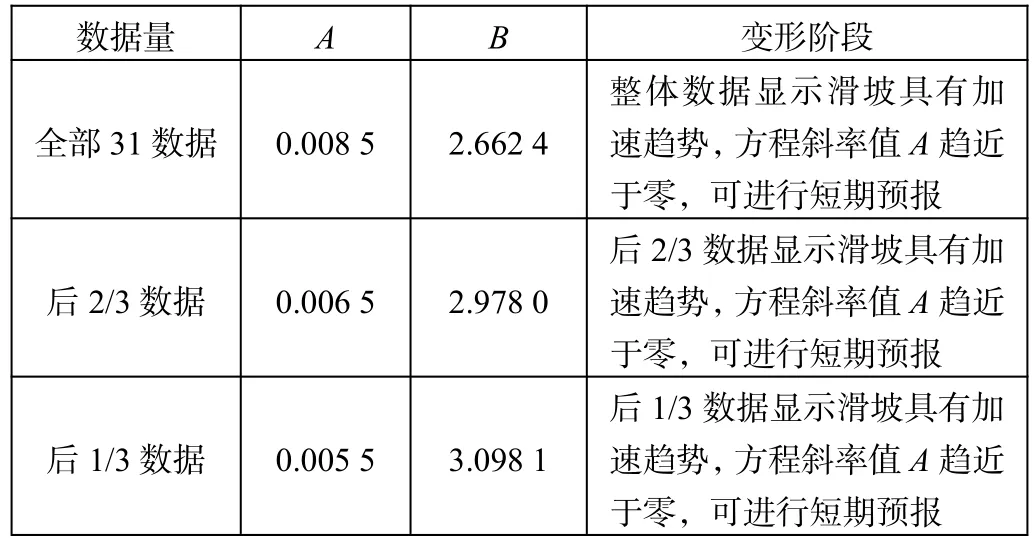
表4 切线角法滑坡变形阶段分析
利用切线角法对滑坡的变形阶段进行分析是使用较为广泛的方法,但是,受坐标单位的影响,用不同单位求得的切线角差别往往过大,有时甚至会造成误判。例如,本文所监测的数据是以日为单位,如果监测时间很长,以周或以月为单位重新拟合插值曲线,便会存在差异。有研究人员改进了切线角法,并提出了相应的预警依据。但是,由于滑坡位移监测曲线呈现出一定的波动,所以,还需要结合专业人员的经验综合判断得到的位移数据。
4 结论
本文选取了某新建工程为期一个月的滑坡位移监测数据,利用三次样条插值法对该数据进行了曲线拟合,并对缺失点进行了数据插值。对比原始数据曲线可知,该插值法拟合效果比较好,利用t检验法检测插值数据,验证了插值数据与原始数据不存在明显差异,可将原始数据与插值数据相结合,构成累计位移新数据列,并利用切线角法对新数据列进行滑坡变形阶段分析。结果表明,该滑坡具有加速趋势,方程斜率值A趋近于零,可进行短期预报。
[1]许小勇,钟太勇.三次样条插值函数的构造与Matlab实现[J].兵工自动化,2006,25(11):76-78.
[2]王文周.改良t检验法[J].西华大学学报:自然科学版,2008,27(6):91-94.
[3]杨庆义,孙政.滑坡变形阶段的划分及短期预报研究[J].科学之友,2011(3):8-10.
[4]许强,曾裕平,钱江澎,等.一种改进的切线角及对应的滑坡预警判据[J].地质通报,2009,28(4):501-505.
TP301.6
A
10.15913/j.cnki.kjycx.2017.20.016
2095-6835(2017)20-0016-03
黄小研(1993—),女,陕西人,硕士研究生,研究方向为机械制造及其自动化。
〔编辑:白洁〕
