上好章节起始课开启课改一扇窗

薛秋萍

摘要：本文以初中数学《生活中的不等式》为例，探讨了初中数学章节起始课教学的“基本套路”，让学生初步建立起对本章知识的整体把握，重视学习方法的引导，渗透基本的研究方法，激发学生的学习兴趣，同时指出了如何注重先行组织者的使用，加强逻辑连贯的学习过程以及与单元整体教学的区别。

关键词：章节起始课；认知结构；生活中的不等式

中图分类号：G633.6文献标识码：A 文章编号：1992-7711（2017）17-039-2

新课改后，各版本的教材都会在每章的开头刊登一些数学名言、背景图片、数学史料等材料，这作为一章内容的“先行组织者”和“导游图”，让学生对即将学习的内容有一个大概的了解，从而更好地促进有意义学习。为了凸显起始课在教学中作用，笔者下面呈现“常规课”和“起始课”两种不同的教学设计课例——“生活中的不等式”，并由此探讨两种教学设计之间的区别。

一、常规设计课例——生活中的不等式

（一）情境创设

小磊和他的妈妈、爸爸的体重分别为30kg、55kg和75kg。春节期间，去瘦西湖游乐场玩跷跷板。小磊和妈妈玩时，谁会向上跷？若小磊和妈妈坐一头，爸爸坐在另一头时，谁会向上跷？

生：这说明：因为30kg55kg（填写不等号），所以会向上跷；

又因为30kg+55kg75kg（填写不等号），所以会向上跷。

师：在日常生活中，同类量（如长度与长度，质量与质量，速度与速度）之间常常存在不等关系。

（二）合作交流解读探究

1.用数学式子表示下面数量之间的关系：

某种袋装牛奶中，每100克牛奶含x克蛋白质，y克脂肪、该牛奶的营养成分含量如下表。

营养成分含量

蛋白质≥29克

脂肪≥31克

非脂乳固体≥81克

生：x≥29，y≥31；

2.概念：

师：像30kg<55kg、x≥29，y≥31，x+2<48、a≤100、3y≥10等，用不等号表示不等关系的式子叫做不等式。

（三）例题讲解巩固提高

例1用不等式表示：

（1）a是正数；（2）b是非负数；

（3）x与3的差不大于2；（4）y的一半与7的和不小于-5。

例2用适当的符号表示下列关系：

（1）x的5倍与3的差比x的4倍大；（2）x的3倍不小于y的8倍。

例3用“>”或“<”号填空：

（1）-6+4-1+3；（2）5-20-2；

（3）6×23×2；（4）-6×（-4）-2×（-4）。

（四）练习巩固

出示一些与例题类似的习题，以此巩固所学知识与方法。

（五）经验归纳

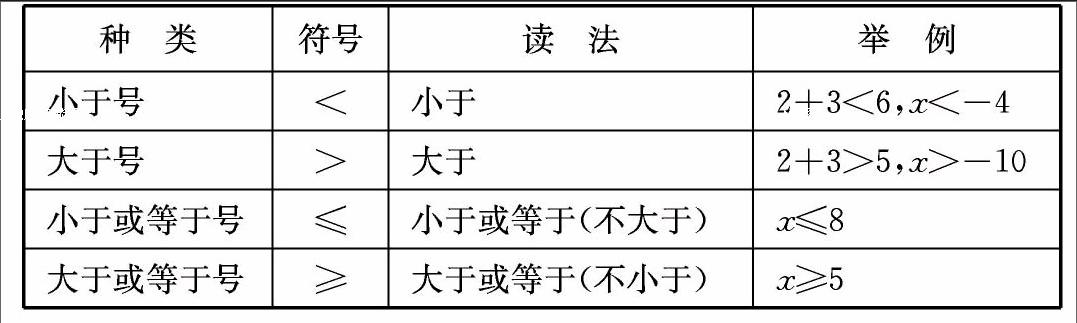
根据不等式的意义，常用的不等号有下面的4种形式。

种类符号读法举例

小于号<小于2+3<6，x<-4

大于号>大于2+3>5，x>-10

小于或等于号≤小于或等于（不大于）x≤8

大于或等于号≥大于或等于（不小于）x≥5

评价反思：

这样的教学设计，学生通过学习，会用不等式表示不等关系，并在现实情境中认识数量间的不等关系，理解不等式的意义。但由于设计时仅仅局限于本章的第一课时内容——生活中的不等式，几乎不关注知识的框架、知识生成过程等，这就使学生压根不知本章不等式要学习哪些相关知识？为什么要学这些相关知识？它与学过的哪些知识有联系，需要用怎样的方法学这些数学知识？学生们只是被动接受，被动学习，从而导致知识面较窄，不能熟练地实现新旧知识的联系。

著名的美国教育心理学家奥苏伯尔在他的著作中写道，如果把所有的教育心理学知识总结为一句话的话，那就是搞清学生已经知道了什么，并且根据这一情况组织教学。正是基于这个理念，他提出了认知同化论的观点，以及先行组织者原则。他认为，在学习一些新的内容之前，先介绍一些恰当、蕴含性广的引导性材料，在已学知识与未学知识之间架起一座桥梁，帮助学生确定有意义学习的方向，增强已学与即将学的知识间的联系与可辨别性，防止干扰。由于这些材料是在学习新知之前呈现的，因此它们又被称为先行组织者。笔者认为，学习与旅行相类似，章节起始课是一章教学内容的开篇，是这部分教学内容的先行者。在章節起始课教学中，教师应该成为一名合格的导游，带领自己的学生经历这样的行程：这一章开篇要建立哪些相关的知识？为什么要建立这些相关知识？它与学过的哪些知识有联系，需要用怎样的方法建立这些数学知识？

于是，我们从情境创设这一环节入手修改，充分利用书本的导言，精心设计，力争帮助学生构建良好的认知结构。在起始课上，老师通过融进数学思想，不断培养和提高学生的数学素养。

二、起始课教学课例——生活中的不等式

（一）情境创设

教师带领学生阅读课本上本章的导言，并布置学生活动任务。

一只纸箱质量为1kg。当放入一些苹果（每个苹果的质量为025kg）后，箱子和苹果的总质量不超过10kg。

（1）填表：

苹果数1020253035

总质量/kg

（2）估计这只纸箱内最多能装多少个苹果？

任务1.独立完成（1）、（2）两小题；

任务2.组内交流，组长收集组员的不同方法；

任务3.各组长展示分享成果。

生：我通过列举法，找到了答案。

师：此种方法的局限在哪里？

生：若数据很大时，不易找到答案。

生：我假设苹果和箱子共重10kg，再利用前面所学得一元一次方程来做。具体方法：设装了x个苹果，得到方程：1+025x=10，解得x=36，所以纸箱内最多能装36个苹果。

师：非常棒！前面一章我们了解到可以用方程模型解决生活中相等关系的问题，这位同学将题目中的不等关系假设成相等关系再利用方程求解。

生：我模仿方程解应用题的方法：设装了x个苹果，根据条件箱子和苹果的总质量不超过10kg，得到：1+025x≤10，再模仿解方程求解的方法，获取答案x≤36。

师：棒极了！老师告诉你，你已经成功掌握学习本章知识的方法了！祝贺你！

师：本章我们将一起解决生活中含有不等量关系的问题。刚才那位同学的大胆尝试，同学们大致了解本章的学习内容了吧！哪位同学来说说？

生：类比一元一次方程，我觉得我们将学习不等式的定义、不等式的解、解不等式以及解决问题。

师：很好，下面请同学翻到本章的目录，看一看，你刚才猜对了吗？你打算怎么学习本章内容？

生：跟方程作类比就可以了。

师：那么，下面我们一起先去认识不等式，了解不等式的概念。

（学习不等式的过程略）

评价反思：

在本章起始课的教学设计中，老师们巧设一个问题情境引导学生回顾旧知，通过类比，启发学生勾画出关于不等式所要学的内容、研究的问题、过程与方法。这样，学生不仅明确了类比的对象，也逐渐掌握数学研究与发现的“基本套路”，让主动思考成为一种习惯。运用类比的方法进行探索学习，大部分学生不仅能够在头脑中对一章内容形成一个大概框架，同时，还能让学生经历概念的发生和发展直至应用的全过程，与常规的教学设计相比，其优越性是显而易见的。

奥苏贝尔的“先行组织者”理论认为：在学习新的知识之前，教师应该从学生已有的认知出发，在新旧知识之间架起一个桥梁，帮助学生把新知识组织和纳入到自己的认知结构中，更好的同化新知识，促成有意义的学习。只有这么做，教学才能致力于本源。广大教师应不拘囿于固有的观念，改变教学方法，上好章节起始课，开启课改一扇窗。endprint