基于杂散光抑制要求的光学表面粗糙度控制方法研究∗

2017-10-23宋延松杨建峰李福马小龙王红2

物理学报 2017年19期

关键词：主镜空间频率散光

宋延松杨建峰李福马小龙王红2)

1)(中国科学院西安光学精密机械研究所,西安 710119)

2)(中国科学院大学,北京 100049)

基于杂散光抑制要求的光学表面粗糙度控制方法研究∗

宋延松1)2)†杨建峰1)李福1)马小龙1)王红1)2)

1)(中国科学院西安光学精密机械研究所,西安 710119)

2)(中国科学院大学,北京 100049)

光学表面加工误差引起的散射是影响光学系统成像性能的重要因素.描述表面总散射能量的均方根粗糙度是评定光学表面粗糙度的通用指标,但因其未能体现散射能量的空间分布,在表征光学表面散射对具体光学系统杂散光性能影响时存在准确度不足的局限.本文基于全积分散射及双向散射分布函数理论,针对杂散光抑制要求提出一种光学表面粗糙度控制的新方法.首先通过分析确定光学表面纹理中影响系统杂散光的空间频率范围,然后度量该频率带限范围内的表面均方根粗糙度,作为控制光学表面粗糙度的指标.以太阳磁场望远镜(MFT)为例进行方法验证,确定主镜表面纹理有效频率范围为0—18 mm−1,分析了主镜表面带限均方根粗糙度对MFT杂散光性能的影响.结果表明,带限均方根粗糙度与MFT杂散光性能之间的关系稳定性能大幅提高,由此验证了采用带限均方根粗糙度描述光学表面粗糙度,能更为准确地控制其对具体光学系统杂散光性能的影响.

表面粗糙度,杂散光,全积分散射,双向散射分布函数

1 引言

随着光学软件优化算法不断成熟,光学系统成像性能越来越依赖于光学表面的加工精度［1−4］.光学元件投产前,需要提供特定表面甚至全部表面的粗糙度指标数据,以保证光学表面抛光精度满足系统成像性能要求.常用的确定粗糙度指标的方法是:首先基于全积分散射(total integrated scattering,TIS)理论建立表面均方根粗糙度σλ与双向散射分布函数(bidirectional scattering distribution function,BSDF)之间的关系［5,6］,或者基于Harvey-Shack表面散射理论建立σλ与角度扩散函数(angle spread function,ASF)之间的关系［7,8］,然后将不同σλ下的BSDF(或ASF)数据输入光学分析软件,分析系统的杂散光性能,根据系统杂散光抑制要求确定表面粗糙度指标σλ,其中,λ代表入射光波长.但本文通过分析发现,σλ作为表面粗糙度指标在控制光学表面散射对系统杂散光性能的影响时具有一定的局限性.一方面,σλ对应过宽的空间频率范围0—1/λ,使得加工厂商在对其测量时面临较大困难［9］;另一方面,表面纹理分解的一系列傅里叶分量中,只有0—1/λ频段内某一子区间分量的散射光能够到达探测器,致使在0—1/λ频段度量的σλ无法准确表征散射光对系统杂散光性能的影响.

针对以上问题,本文提出一种针对杂散光抑制要求控制光学表面粗糙度的新方法.该方法确定了表面纹理中对系统杂散光有影响的空间频率范围,并将该频率带限范围内度量的均方根粗糙度σλ–s作为控制表面粗糙度的指标,以有效解决用σλ作为表面粗糙度指标时存在的两个问题.

2 表面粗糙度影响的理论基础

2.1 TIS与σλ之间的关系

如图1所示,实际光学表面具有随机高度起伏,经其反射后的总能量Pt包括镜面反射能量Ps和散射反射能量Pd两部分.TIS定义为散射反射能量与总反射能量之比.表面粗糙程度通常用表面高度的均方根粗糙度［10］(root-mean-square roughness,σrms)来衡量.1961年,Bennett和Porteus假设表面高度服从高斯分布,推导出了两者之间的关系［11］:

其中,θi是入射角,λ是入射光波长.

图1 表面散射示意图Fig.1.Schematic of surface scattering.

由于正弦光栅衍射同样满足(1)式,且表面散射可看作无数个不同空间频率正弦光栅衍射的叠加,所以(1)式不受限于表面高度分布形式,适用于任何表面散射量计算［12］.根据光栅方程可知,衍射角θs、入射角θi满足sinθs−sinθi=mλf,当光栅空间频率f＞1/λ时,其衍射的能量不会对TIS有影响,因此σrms对应表面纹理的空间频率范围为0—1/λ.为突出σrms是入射光波长的函数,一般将其记为σλ.本文研究的对象是经过抛光后的光学表面,这类表面一般满足σλ≪λ,此时(1)式近似为［13,14］

对于正弦反射光栅,TIS等于所有非零级衍射总能量与总反射能量之比.当光栅满足σλ≪λ时,±1级衍射光能量占总反射能量Pi的比例［10］为

其中,Pi为入射光功率,R为表面反射率,P1和P−1分别为+1,−1级衍射光能量.

对比(2)和(3)式可知,当表面满足σλ≪λ时,计算TIS只需考虑±1级衍射光,因此本文推导分析过程中所使用的光栅方程均针对±1级衍射光.

2.2 TIS与BSDF之间的关系

描述散射光能量空间分布的BSDF定义为散射亮度与入射照度之比.Harvey等研究得出,对于干净、各向同性的光滑表面(σλ≪λ),BSDF在方向余弦空间具有位移不变性,可以用Harvey-Shack模型描述［15−17］:

其中,βs和βo分别为散射方向、镜面反射方向的单位向量在光学表面上的投影,如图2所示.b0,l,s为模型的三个参数,用于拟合实际测量的BSDF数据,所代表的含义如图3所示.

图2 Harvey-Shack模型中的向量Fig.2.Direction vectors used in the Harvey-Shack model.

图3 Harvey-Shack模型,b=0.1,l=0.001,s=−1.5Fig.3.Harvey-Shack model whereb=0.1,l=0.001,s=−1.5.

根据TIS以及BSDF的定义可知,TIS等于BSDF在半球空间内对立体角的积分.杂散光分析需要考虑整个光学表面的散射,而BSDF与入射角有关,入射角是表面位置、表面形状以及光线入射离轴角的函数,因此利用BSDF精确计算表面所有位置的TIS是不现实的.通过(2)式可知,正入射时TIS取得最大值,若各位置的散射量取该值时系统杂散光分析结果满足抑制要求,则实际杂散光性能一定满足杂散光抑制要求,故分析时可用此值代替各位置实际TIS.光线正入射时,TIS的解析解为［5］

(5)式可作为杂散光分析时TIS与BSDF之间的一般表达式.

2.3 σλ控制表面粗糙度的局限性

工程上利用(2)和(5)式确定表面均方根粗糙度σλ的一般方法如下.

1)计算σλ与BSDF的关系表达式.联立(2)和(5)式可得σλ与BSDF关系如下:

2)参数l,s取值.抛光光学表面的功率谱密度多具有分形特征［10,18］,满足l≪|βs−βo|,因此l需取足够小值,以忽略其对TIS的影响［19,20］;s一般根据经验在−0.5—−2.5内取典型值.

3)确定σλ.将不同σλ对应的BSDF数据输入光学分析软件进行杂散光性能分析,满足系统杂散光抑制要求的σλ即所求表面粗糙度指标.

利用以上方法可确定σλ,但用σλ控制表面粗糙度存在以下两个问题.

问题一:σλ不能准确控制表面散射对系统杂散光的影响.

表面功率谱密度函数(power spectral density,PSD)是描述实际加工表面纹理的有效手段.如前所述,σλ对应的空间频率范围为0—1/λ,在二维频率空间中对应半径1/λ的圆域,如图4中SA所示,利用PSD(fx,fy)计算σλ的公式［12］为

如图5所示,对表面任意一点(如Q)而言,只有位于Ω立体角内的散射光线能够到达探测器,从而影响系统杂散光性能.根据光栅方程,Ω对应的空间频率域是SA的一个子集,类似图4中SB,因此SB是杂散光分析时需要关心的有效空间频率范围,此带限范围内度量的均方根粗糙度为σλ−s,其计算公式为:

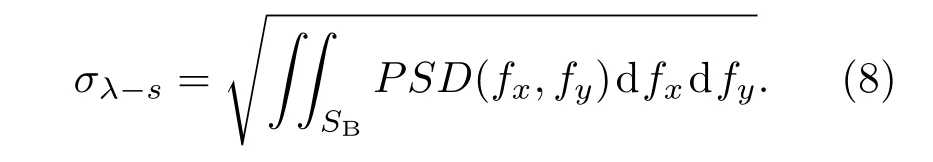
图4 σλ,σλ−s所对应的表面PSD区域Fig.4.Integral areas of PSD for calculating σλ,σλ−s.

图5 对系统杂光有影响的散射光线分布Fig.5.Distribution of scattering light which received by detector.

图6 (网刊彩色)具有相同σλ的三条不同PSD曲线Fig.6.(color online)Three di ff erent PSD curves which have the same σλ.

对比(7)和(8)式可知,由于积分域的差异,σλ相同的光学表面σλ−s不一定相同.图6为三个不同表面所对应的功率谱密度曲线,它们在0—1/λ内的包围面积相等,但在诸多有效空间频率范围(假设0.01/λ—0.1/λ)内的包围面积明显存在差异,表明使用σλ相同的三个表面,系统将会产生不同的杂散光性能.因此σλ不能准确控制表面散射对系统杂散光性能的影响.

问题二:实际测量验证σλ非常困难.

如图7所示,对于各向同性光学表面,要获得0—1/λ范围内的表面功率谱密度函数,需要四台不同的仪器［21］,这对于加工厂商而言,常常是做不到的,因此很难验证加工完成的光学表面是否满足指标σλ.

通过以上分析可知,为使粗糙度指标更有效、更方便测量,应首先确定对系统杂散光有影响的空间频率范围,进而给出此范围内的表面粗糙度指标σλ−s.

图7 (网刊彩色)通过四台仪器获得的PSD函数［21］Fig.7.(color online)The PSD function determined from four di ff erent metrology instruments.

3 基于带限均方根粗糙度的表面控制方法

由图2可知,散射方向、镜面反射方向单位向量在光学表面上的投影分别为

其中,θs和φs分别为散射光线的仰角和方位角,θo和φo分别为镜面反射光线的仰角与方位角.

令αd=sinθscosφs,βd=sinθssinφs,αo=sinθocosφo,βo=sinθosinφo,则有

根据广义光栅方程

得到空间频率

联立(11)和(13)式可得

利用几何光线追迹方法求得|βs−βo|取值范围后,通过(14)式即可确定表面纹理中对系统杂散光有贡献的空间频率范围.此频率带宽内分量引起的散射光线只分布在立体角Ω内,故称之为部分积分散射(partial integrated scattering,PIS).在方向余弦空间,微元dΩ=sinθsdθsdφs=dαddβd/cosθs,图5中立体角Ω内的散射能量为

图8 计算PIS的积分区域Fig.8.The integral area for calculating PIS.

将(4)式式代入(16)式,得到PIS的解析表达式:

当|βs−βo|min=0,|βs−βo|max=1时,(17)式转化为(5)式,因此TIS只是PIS的特殊情况.

鉴于(2)式适用于任意光滑表面,因此也适用于PIS的计算,此时表面粗糙度由σλ−s代替:

联立(17)和(18)式,可得到σλ−s与BSDF的关系式. 利用杂散光分析软件分析不同σλ−s下的杂散光性能,可确定表面粗糙度指标σλ−s,此时σλ−s对应的频带宽度为

下面以MFT为例,验证新方法在控制表面粗糙度方面的有效性.

4 实例分析

MFT是中国2011年提出的深空太阳天文台计划的主载荷,其望远镜部分由1 m口径抛物面主镜和透射式准直镜组成.图9是MFT的主成像光路示意图,表1是MFT的光学指标参数.太阳对MFT张角Φ32′,远大于MFT视场2.8′×2.8′,因此主镜接收到的能量中绝大部分为视场外能量,其表面散射会严重降低系统信噪比［22］,必须对主镜粗糙度提出指标要求,以实现MFT的高性能成像.光学表面二阶杂散光能量远小于一阶杂散光,故理论分析时只需考虑主镜表面一阶散射.

图9 MFT主成像光路示意图Fig.9.Schematic of optical path of MFT.

表1 MFT光学参数Table 1.Optical parameters of MFT.

MFT主镜表面粗糙度计算过程如下.

1)计算|βs−βo|min,|βs−βo|max.

如图10所示,平行光束经主镜聚焦于点(xi,yi,zi).对点(x0,y0,z0)而言,其镜面反射光线方向向量记为r0,散射光线方向向量记为r01,它们与一次像面的交点分别为(xi,yi,zi),(x1,y1,z1).因主镜是MFT的入瞳,所以对于主镜任意一点而言,它的空间域Ω就是视场光阑开口对该点的立体角.

图10 MFT主镜散射路径示意图Fig.10.Schematic of scattering path of primary mirror.

在(x0,y0,z0)点建立新坐标系xnewynewznew,选取该点法线方向为znew轴,入射面为ynewznew平面,根据右手法则确定xnew轴,如图10所示.r0,r01可表示为

新坐标系三个坐标轴的单位向量可取为

新坐标系与原始坐标系的转换矩阵M为

散射光线r01与镜面反射光线r0在新坐标系下的单位向量r01new,r0new分别为:

式中(α01,β01,γ01),(α0,β0,γ0) 分别为r01new,r0new的向量坐标.

结合(11)式得到:

2) 建立σλ–s与b0,s的函数关系

将|βs−βo|min=0,|βs−βo|max=10−2代入(17)式,得

正如前文所述,l取值应足够小,此处可取为0.0001.联立(18)和(27)式,可得σλ−s与b0,s的函数关系:

3)σλ−s对MFT杂散光性能影响分析

利用(28)式计算出主镜不同σλ−s下的BSDF数据后,使用Tracepro软件分析σλ−s对MFT杂散光性能的影响.点源透过率函数(PST)是描述系统杂散光性能的常用手段,图12绘制了s=−1.5,l=0.0001时,PST随σλ−s的变化关系.由图可知,σλ−s越大,PST曲线值越高,代表MFT杂散光性能越差.为达到PST＜10−4的设计目标,主镜带限均方根粗糙度σλ−s应小于0.03 nm.

图12 (网刊彩色)不同σλ−s取值下的PST曲线Fig.12.(color online)The PST curves with di ff erent σλ−s.

基于PST＜10−4的杂散光抑制要求,确定了两种主镜表面粗糙度指标σλ−s与σλ,见表2.指标确定过程中s取典型值−1.5,但光学表面抛光时s值很难控制,一般会在−2.5—−0.5之间波动,因此PST曲线对s值波动的抵抗能力能够反映两种指标在控制表面粗糙度方面的有效性.图13分别绘制了两种指标下,系统PST曲线随s的变化关系.由图可知,当s在−2.5—−0.5之间波动时,σλ−s控制下PST最大值的波动范围小于一个数量级,且都满足PST＜10−4;σλ控制下PST最大值的波动范围接近三个数量级,且出现了PST＞10−4的情况.综上可知,带限均方根粗糙度σλ–s与PST之间关系更加稳定,能更准确地控制表面粗糙度对系统杂散光性能影响.

表2 表面粗糙度指标Table 2.Surface roughness indexes.

图13 (网刊彩色)采用不同方法确定的指标,PST对s波动的抵抗能力 (a)σλ−s;(b)σλFig.13.(color online)The resistance against slope s of PST with the RMS roughness determined by(a)σλ–s;(b)σλ.

5 结论

光学人员能熟练使用光学分析软件对已知光学表面属性的光学系统进行杂散光性能分析,但在根据系统杂散光抑制要求为光学表面提供粗糙度控制指标时依然面临一些困难.本文提出的控制表面粗糙度方法,采用带限均方根粗糙度σλ−s作为粗糙度指标,经理论推导和实例分析表明:由于明确了表面纹理中对系统杂散光有影响的空间频率范围,σλ−s能更准确地控制表面散射对系统杂散光性能的影响,且易于测量,适合作为光学人员与加工厂商之间使用的粗糙度指标.该研究对于工程上如何控制光学表面散射对系统杂散光的影响具有指导意义.

本文为得到PIS的解析表达式(17),将光学表面各位置的积分域统一为同一圆环域,意味着人为放宽了表面空间频率范围,从而出现PST曲线随s变化而轻微波动的现象,如图13(a)所示.下一步可以针对每个离轴角分别求解PIS,得到更为精确的表面纹理空间频率范围,从而进一步减小PST随s变化的波动性.

［1］Harvey J E,Lewotsky K L,Kotha A 1995Appl.Opt.34 3024

［2］Yang W,Huang W,Xu W C,Shang H B 2013Acta Opt.Sin.33 0922001(in Chinese)［杨旺,黄玮,许伟才,尚红波2013光学学报33 0922001］

［3］Tan N Y,Xu Z J,Wei K,Zhang Y,Wang R 2017Acta Phys.Sin.66 044201(in Chinese)［谭乃悦,许中杰,韦可,张月,王睿2017物理学报66 044201］

［4］Harvey J E 2013Proc.SPIE8862 88620Q

［5］Fest E C 2013Stray Light Analysis and Control(Washington:SPIE)pp64–70

［6］Gallagher D,Wu Z,Larson B,Nelson P G,Oakley P,Sewell S,Tomczyk S 2016Proc.SPIE9906 990654

［7］Harvey J E,Thompson A K 1995Proc.SPIE2576 155

［8］Krywonos A,Harvey J E,Choi N 2011J.Opt.Soc.Am.A28 1121

［9］Dittman M G,Grochocki F,Youngworth K 2006Proc.SPIE6291 62910P

［10］Stover J C 1995Optical Scattering:Measurement and Analysis(Bellingham:SPIE)pp32–38

［11］Bennett H E,Porteus J O 1961J.Opt.Soc.Am.A51 123

［12］Stover J C 2012Proc.SPIE8495 849503

［13］Choi N,Harvey J E 2012Proc.SPIE8495 849504

［14］Harvey J E,Schroeder S,Duparré A 2012Opt.Engineer.51 013402

［15］Stray Light Analysis in ASAP,Breault Research Organization http://wwwbreaultcom/［2017-4-10］

［16］Harvey J E 1977Proc.SPIE107 41

［17］Harvey J E,Vernold C L 1997Proc.SPIE3141 113

［18］Church E L 1988Appl.Opt.27 1518

［19］M1 Microroughness and Dust Contamination,Hubbard R http://atst.nso.edu /sites/atst.nso.edu/ fi les/docs/TN-0013-D.pdf［2017-4-7］

［20］Stray Light Analysis,Gallagher D http://mlsohaou caredu/COSMO/Sections/16%20-%20COSMOLC-DE-7003%20(Straylight%20Analysis).pdf［2017-3-30］

［21］Harvey J E,Choi N,Krywonos A 2009Proc.SPIE7426 74260I

［22］Danilovic S,Gandorfer A,Lagg A Schüssler,Solanki S K,Vögler A,Kastsukawa Y,Tsuneta S 2008Astron.Astrophys.484 L17

Method of controlling optical surface roughness based on stray light requirements∗

Song Yan-Song1)2)†Yang Jian-Feng1)Li Fu1)Ma Xiao-Long1)Wang Hong1)2)
1)(Xi’an Institute of Optics and Precision Mechanics,Chinese Academy of Sciences,Xi’an 710119,China)
2)(University of Chinese Academy of Sciences,Beijing 100049,China)

Scattering introduced by optical surface fabrication errors could degrade optical performance severely.Therefore,the optical designers are required to provide a roughness index for describing the speci fi c surface or even all surfaces to ensure the fi nal imaging performance.The surface root-mean-square(RMS)roughness is a common index to quantify surface topography.And there are also some available methods to acquire the surface RMS roughness based on bidirectional scattering distribution function theory or the angle spread function theory.However,the in fl uence of the optical surface scattering on the optical system cannot be accurately revealed by the surface RMS roughness determined by these methods.On the one hand,the RMS roughness corresponds to an excessively wide spatial frequency range from 0 to 1/λ,whereλis the wavelength of the light.Consequently,it is difficult to measure the RMS roughness during manufacture.On the other hand,what really worsens the stray light performance of the system is only the surface pro fi le located within a certain subinterval of the aforementioned frequency range,to put it in another way,the surface RMS roughness identi fi ed by the methods above is incompetent to quantify the amount of the energy that is surfacescattered to the detector.To address the issues above,in this paper we propose a novel approach to identifying the surface roughness.This method seeks to deduce the relation between optical surface RMS roughness and the stray light requirement of the system by dint of partial integrated scattering(PIS).In contrast to total integrated scattering,PIS counts the scattering light energy that could reach the detector.Hence,the RMS roughness identi fi ed in this way corresponds to the e ff ective spatial frequency range that contributes to the stray light in the system.Firstly,the e ff ective frequency range concerned with the system stray light level is identi fi ed through the analysis of the propagation path of the scattered light.Then,the surface RMS roughness would be measured within the established range according to the stray light requirement of the system and used to control the surface roughness as the roughness index during the optical manufacture process.The method not only considers the scattering as the surface characteristic,but also takes into account the in fl uence of scattering on the system.Taking the solar magnetic fi eld telescope(MFT)for example,the validity of the method is veri fi ed by comparing with the traditional methods.As manifested in the outcome,the e ff ective frequency range of primary mirror is from 0 to 18 mm−1,and the surface RMS roughness identi fi ed in such a new way can stage the stray light performance of MFT in a more precise manner,which is more reliable to serve as a surface roughness index.

surface roughness,stray light,total integrated scattering,bidirectional scattering distribution function

26 March 2017;revised manuscript

17 July 2017)

(2017年3月26日收到;2017年7月17日收到修改稿)

10.7498/aps.66.194201

∗国家自然科学基金(批准号:U1231204)资助的课题.

†通信作者.E-mail:syansong@163.com

PACS:42.25.Fx,42.15.–i

10.7498/aps.66.194201

*Project supported by the National Natural Science Foundation of China(Grant No.U1231204).

†Corresponding author.E-mail:syansong@163.com