支撑剂在滑溜水中的运移规律研究
2017-10-20赵俊
赵俊
(中联煤层气有限责任公司,北京 100011)
赵银明
(长江大学信息与数学学院,湖北 荆州 434023)
陈仙江
(中石油新疆油田分公司开发公司,新疆 克拉玛依 834000)
支撑剂在滑溜水中的运移规律研究
赵俊
(中联煤层气有限责任公司,北京 100011)
赵银明
(长江大学信息与数学学院,湖北 荆州 434023)
陈仙江
(中石油新疆油田分公司开发公司,新疆 克拉玛依 834000)
页岩气藏压裂中大量使用低黏滑溜水压裂液,支撑剂在其中的沉降运移规律不同于以往的高黏压裂液,因此需要进行针对性研究。Stokes沉降公式只是考虑单颗粒支撑剂在静止液体中的沉降,没有考虑压裂液输送支撑剂的动态过程,为此进行了公式修正。在此基础上给出大量颗粒干扰沉降时沉降速度与加砂浓度的关系式,同时对影响沉降速度的主要因素,如滑溜水黏度、支撑剂粒径和密度、排量及加砂浓度等进行敏感性计算分析。与室内试验结果对比表明,所用理论方法准确可靠。理论计算进一步表明,采取变黏度压裂液体系和优化施工排量等工艺措施,能够获得较长的支撑裂缝和较大的有效改造体积,为今后的压裂设计和施工优化提供了理论参考。
滑溜水;支撑剂;沉降速度;运移;敏感性
随着美国页岩气革命的发生,在石油天然气能源领域引起了极大的震动,也在全世界掀起一场能源革命,为新能源的发展指明了方向[1~4]。继北美地区之后,我国已成为商业性开发页岩气的第3个国家。随着我国页岩气藏的大规模开发,水力压裂作为主要的开发技术越来越受到重视[5,6]。不同于常规储层,在页岩气藏中的水力压裂,多采用滑溜水压裂液,并且用量往往达上万方,输送支撑剂近千方。由于滑溜水黏度较低,近似于清水,因此支撑剂在滑溜水中的运移规律将不同于以往的高黏压裂液[7,8]。另外,考虑到降低压裂成本和缓解用水紧张以及环保等多方面的问题,在保证加砂量相同的前提下,应尽可能减少滑溜水的用量。为此,笔者针对支撑剂在滑溜水中的运移规律进行了深入研究[9~11]。
1 理论模型
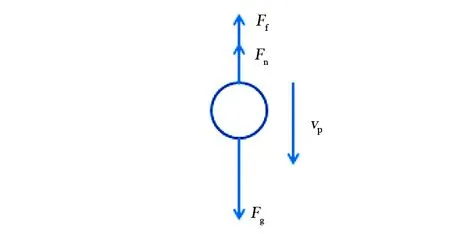
图1 单个支撑剂的沉降

图2 支撑剂颗粒在裂缝内的运移
对于支撑剂在压裂液中的沉降,目前多采用Stokes沉降公式。该公式是以单颗粒支撑剂在静止液体中的沉降为假设前提,综合考虑重力(Fg)、浮力(Ff)和黏滞力(Fn)而推导出来的,如图1所示。在实际的水力压裂过程中,压裂液是连续流动的,并不是静止不动。同时,并不是单一颗粒支撑剂在沉降,而是大量的颗粒相互干扰,成簇或成团沉降[12,13]。因此,Stokes沉降公式并不能真实反映出支撑剂在压裂液中的沉降,需要进行修正完善。
支撑剂依靠压裂液的携带并沿着裂缝延伸方向,被输送运移到一定的位置。在该过程中,支撑剂逐渐沉降到裂缝底部,并不断堆积形成砂堤,如图2所示。支撑剂单颗粒在压裂液中沉降初期,由于受到重力作用加速向下,所受黏滞阻力不断增大。两者很快达到平衡,沉降处于匀速状态,这一速度称为自由沉降速度[14,15]。根据雷诺数:
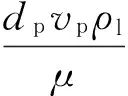
(1)
的大小不同,也即颗粒所处压裂液中的流态不同,自由沉降速度的计算分别如下:
当NRe≤2,即压裂液流动保持层流时,单颗粒支撑剂的自由沉降速度为:

(2)
式中,vp为单颗粒支撑剂的自由沉降速度,m/s;dp为支撑剂颗粒的直径,m;g为重力加速度,m/s2;ρp为支撑剂的视密度,kg/m3;ρl为压裂液的密度,kg/m3;μ为压裂液黏度,Ps·s。
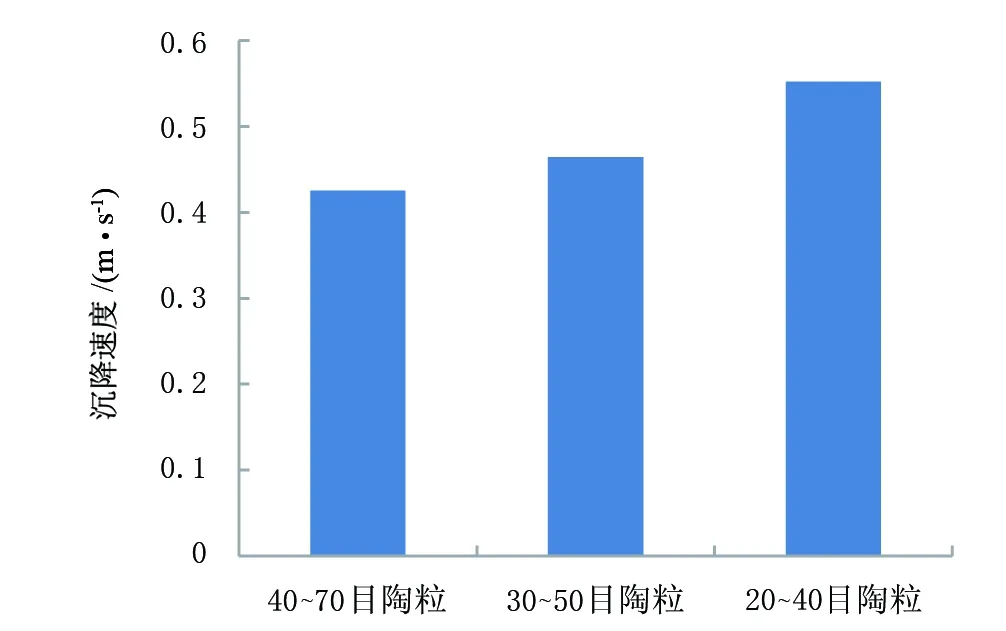
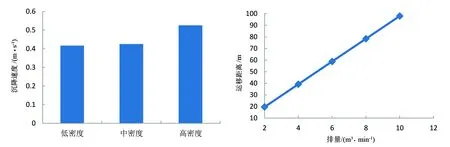
当2 (3) 当NRe>500,即压裂液流动保持紊流时,单颗粒支撑剂的自由沉降速度为: (4) 支撑剂在裂缝延伸方向上的位移为: (5) 式中,Lh为单颗粒支撑剂沿裂缝长度方向上的运移距离,m;tp为支撑剂从裂缝顶部沉降到底部的时间,s;hp为裂缝垂直高度,m。 在实际的水力压裂加砂过程中,大量的支撑剂颗粒聚集在一起,沉降时相互干扰,因此,加砂浓度对支撑剂沉降具有较大的影响。根据加砂浓度的大小,可以对单颗粒支撑剂沉降速度进行修正,具体公式[16]如下: vpe=vp(1-Cp)β (6) 式中,vpe为考虑干扰后的支撑剂最终沉降速度,m/s;Cp为加砂浓度,%;β为干扰指数,与颗粒的沉降雷诺数有关,当NRe≤2时,β=5.5;当2 水力压裂要求尽可能大的有效支撑裂缝体积,因此,沉降速度要尽可能的低,以便将支撑剂输送到更远的裂缝端部。下面讨论压裂液黏度、支撑剂粒径、密度、流速以及加砂浓度等主要因素对支撑剂运移和沉降的影响。 2.1压裂液黏度的影响 在页岩气滑溜水压裂中常用40~70目陶粒,为此笔者以40~70目陶粒为例讨论压裂液黏度对支撑剂沉降和运移距离的影响。假设滑溜水黏度分别为1、2、4、6、10mPa·s,滑溜水密度为1.03×103kg/m3,40~70目陶粒的平均粒径为3.54×10-4m,视密度为2.78×103kg/m3,裂缝高度为20m。 利用式(1)~(6)计算支撑剂在不同黏度滑溜水中的沉降速度,得到黏度对沉降速度和沉降时间的影响,结果如图3所示。由图3可以看出,当黏度从1mPa·s提高到10mPa·s时,沉降速度由0.425m/s降低到0.08m/s,沉降时间由40s增大到240s。可见,随着滑溜水黏度的增大,支撑剂的沉降速度有着比较明显的降低,同时,沉降时间大大延长。 假设裂缝的平均宽度为2mm,施工排量为10m3/min,以裂缝入口处的流速为最大流速,根据单颗粒支撑剂在裂缝中的沉降时间就可以计算出颗粒沿裂缝延伸方向上的最大运移距离,结果如图4所示。由图4可知,黏度对颗粒的运移距离影响较大,黏度越高,输送运移的距离越大。因此,如要获得较长的支撑裂缝,可采用变黏度滑溜水压裂液体系设计,在施工初期采用黏度较高的滑溜水,随着时间的增加,不断降低滑溜水的黏度,最终达到已压开裂缝尽可能被支撑的效果和目的。 图3 黏度对沉降速度和沉降时间的影响 图4 黏度对最大运移距离的影响 支撑剂类别平均粒径/10-4m40~70目陶粒3.5430~50目陶粒4.8820~40目陶粒6.58 图5 支撑剂粒径对沉降速度的影响 2.2支撑剂粒径的影响 支撑剂粒径的大小对沉降速度有着一定的影响,选取3种常用的陶粒支撑剂粒径作为对比,见表1。根据式(1)~(6)可以计算不同粒径所对应的沉降速度(黏度为1mPa·s),结果如图5所示。由图5可知,随着粒径的增大,沉降速度变大,但增加幅度并不大,因此,粒径对沉降速度的影响并不十分明显。 2.3支撑剂视密度的影响 由于支撑剂在压裂液中沉降时,主要受重力和黏滞力作用,因此,支撑剂颗粒的视密度大小对其沉降速度有一定的影响。选取40~70目陶粒,分别以低密度、中密度、高密度3种类型(见表2),以考察视密度大小对沉降速度的影响。根据式(1)~(6)计算不同陶粒视密度的沉降速度(黏度为1mPa·s),结果如图6所示。由图6可知,颗粒视密度差异并不大,视密度对沉降速度的影响也不大。 表2 不同陶粒的视密度 2.4排量的影响 水力压裂施工过程中,排量对支撑剂的水平运移距离有较大影响。选取排量分别为2、4、6、8、10m3/min,假设缝口处的最大流速为压裂液的运动速度,可以得到支撑剂的最大运移距离,结果如图7所示。由图7可知,在压裂液黏度和裂缝高度相同的前提下,随着排量的增加,支撑剂颗粒的运移距离增大比较明显,因此,排量大小对支撑剂的输送距离十分关键。 图6 支撑剂颗粒密度对沉降速度的影响 图7 排量对运移距离的影响 图8 加砂浓度对沉降速度的影响 2.5加砂浓度的影响 假设加砂浓度为25%,计算得到不同滑溜水黏度下的干扰和自由沉降速度,结果如图8所示。由图8可知,颗粒之间的相互干扰降低了沉降速度,这是由于颗粒在沉降时,会引起周围液体的向上运动,起到阻碍周围颗粒下沉的作用。同时,相对于没有加砂的压裂液,砂液混合物的密度和黏度都有明显增大,导致浮力和沉降阻力增大,从而降低沉降速度。 2.6其他因素的影响 对于支撑剂沉降和运移的影响,还有其它因素,如支撑剂类型和圆球度以及加砂方式等。支撑剂类型主要有石英砂、覆膜砂和陶粒等,其主要区别是抗压强度的不同,相对于密度和粒径等对沉降和运移的影响,基本没有差别。 利用平板模型,采用滑溜水和陶粒支撑剂分别模拟不同的流速支撑剂的沉降情况,结果如图9所示。结果表明,随着排量的增大,支撑剂在裂缝内的运移距离在不断增大。在不同的支撑剂粒径和压裂液黏度时,也可以得到类似图9的结果。随着加砂浓度的增大,支撑剂的运移距离也在不断增加;支撑剂粒径越大,沉降速度越大,运移距离越小。这些结果充分证实了上述支撑剂运移理论,与前面理论计算结果比较一致[17]。也进一步表明,施工参数、压裂液性能和支撑剂性能参数等对于支撑剂沉降和运移距离都有较大影响,同时,支撑剂性能参数是影响支撑剂运移的主要因素。 1)考虑压裂液对支撑剂的携带作用,修正了Stokes单颗粒静态沉降公式,可以计算出不同沉降时间下的运移输送距离。当支撑剂大量沉降时,颗粒之间相互干扰,降低沉降速度,考虑加砂浓度的影响,给出相应的沉降速度计算公式。 图9 砂堤形态 2)滑溜水黏度越高,支撑剂沉降速度越小;支撑剂粒径和密度越大,沉降速度越大,但影响幅度不大;施工排量越大,支撑剂运移距离越远;随着加砂浓度的提高,支撑剂沉降受到干扰,沉降速度降低。 3)理论计算结果比较符合实际,表明所用理论方法比较可靠。 4)为了获得较长的裂缝和较大的支撑体积,可以采取变黏度滑溜水体系,施工初期的黏度较高,随后不断降低黏度,最终达到裂缝尽可能被支撑的效果。 [1]Cipolla C L, Lolon E P, Dzubin B. Evaluating stimulation effectiveness in unconventional gas reservoirs[J].SPE 124843, 2009. [2] Cipolla C L, Warpinski N R, Mayerhofer M J, et al. The relationship between fracture complexity, reservoir properties, and fracture treatment design[J].SPE 115769, 2010. [3] 吴奇,胥云,刘玉章. 美国页岩气体积改造技术现状及对我国的启示[J].石油钻采工艺,2011,33(2):1~7. [4] 吴奇,胥云,王腾飞. 增产改造理念的重大变革——体积改造技术概论[J].天然气工业,2011,31(4):7~12. [5] 叶登胜,李建忠,朱炬辉. 四川盆地页岩气水平井压裂实践与展望[J]. 钻采工艺,2014,37(3):42~45. [6] 周德华,焦方正,贾长贵. JY1HF页岩气水平井大型分段压裂技术[J].石油钻探技术,2014,42(1):75~80. [7] 张士诚,牟松茹,秦勇. 页岩气压裂数值模型分析[J].天然气工业,2011,31(12):81~84. [8] 王志刚. 涪陵焦石坝地区页岩气水平井压裂改造实践与认识[J].石油与天然气地质,2014,35(3):425~430. [9] 肖博,张士诚,郭天魁,等. 页岩气藏清水压裂悬砂效果提升实验[J]. 东北石油大学学报,2013,37(3):94~100. [10] 张涛,郭建春,刘伟. 清水压裂中支撑剂输送沉降行为的CFD 模拟[J]. 西南石油大学学报(自然科学版),2014,36(1):74~82. [11] 温庆志,高金剑,刘华,等. 滑溜水携砂性能动态实验[J].石油钻采工艺,2015,37(2):97~100. [12] 孙晓峰,纪国栋,冯松林,等. 幂律流体中岩屑颗粒沉降速度实验[J].断块油气田,2016,23(1):120~124. [13] 张潦源,翟恒立,卢娜娜,等. 非牛顿压裂液中支撑剂聚集沉降规律实验研究[J].科学技术与工程,2013,34(13):10142~10146. [14] 孙海成.脆性页岩网络裂缝中支撑剂的沉降特性[J].油气地质与采收率,2013,20(5):107~111. [15] 王松,杨兆中,卢华,等. 水力压裂中支撑剂输送的数值模拟研究[J].石油天然气学报(江汉石油学院学报),2009,31(5):380~384. [16] 温庆志,胡蓝霄,翟恒立.滑溜水压裂裂缝内砂堤形成规律[J]. 特种油气藏,2013,20(3):137~139. [17]温庆志,罗明良,李加娜,等. 压裂支撑剂在裂缝中的沉降规律[J]. 油气地质与采收率,2009,16(3):100~104. [编辑] 洪云飞 TE357 A 1673-1409(2017)17-0020-06 2017-06-20 国家科技重大专项(2016ZX05066)。 赵俊(1986-),男,工程师,现主要从事油气田增产方面的研究工作;通信作者:赵银明,452667017@qq.com。 [引著格式]赵俊,赵银明,陈仙江.支撑剂在滑溜水中的运移规律研究[J].长江大学学报(自科版), 2017,14(17):20~25.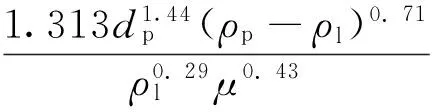

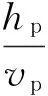
2 敏感性分析




3 模拟试验
4 结论

