基于HHT的电能质量暂态扰动信号检测技术
2017-10-20纪萍吴静妹陈玲
纪萍,吴静妹,陈玲
(河海大学文天学院电气信息工程系,安徽 马鞍山 243000)
基于HHT的电能质量暂态扰动信号检测技术
纪萍,吴静妹,陈玲
(河海大学文天学院电气信息工程系,安徽 马鞍山 243000)
针对电网中暂态扰动信号难以检测这一难题,提出了一种利用HHT(希尔伯特-黄变换)进行处理的新方法。HHT通过经验模态分解法(EMD)和Hilbert变换,在检测非平稳信号的起止时间,频率和幅值有较好的效果。利用HHT分别对暂态谐波、电压中断、电压暂降和电压暂升4类典型的暂态扰动及其复合组合信号进行仿真验证,结果表明该方法可以较准确的实现对电能质量非平稳信号的分析和处理。该研究为电能质量信号的检测提供了新方法,为电网的治理开辟了新思路。
电能质量;暂态扰动信号;希尔伯特-黄变换;经验模态分解法
电力系统大功率设备以及非线性、冲击性负荷的广泛应用,严重污染了电网,影响了电能质量,其中电压中断、电压暂升、电压暂降等暂态电能质量扰动影响最为突出。而随着计算机、微电子、通信等高科技领域的敏感设备增多,人们对电能质量提出了更高的要求。通过有效方法对电网中的暂态扰动数据进行准确的检测和定位,为电力部门分析电能质量问题所在,明确供、用电双方的义务和责任,为电网的综合治理提供了依据,同时为分析动态电压补偿,综合评价电网质量的优劣都有很大的帮助。近几年比较常用的扰动信号检测技术主要是傅里叶变换(FFT)和小波变换。傅里叶变换在分析线性时不变系统具有优势,但是对于非平稳暂态数据的分析,在提取信号的时频域特征时,劣势明显,因此用傅里叶变换分析电网暂态数据很不实用[1]。目前,分析非平稳数据使用较多的是小波变换,在时频域都具有局部化分析的特征,但是由于其数据的检测精度取决于小波基的选择。因此,也有其局限性[2,3]。小波基的选择是在检测系统设计的时候就确定了,不能随着扰动信号的类型做随时变换。因此小波变换的分解效果可能对部分信号效果较高,而检测信号发生变换,不能保证较优的提取效果。为了精确检测电能质量暂态扰动这类非平稳信号,这就要求检测方法在时域和频域都具有较好的局部特性。
希尔伯特-黄变换(Hilbert-Huang Transform,HHT)是美藉华人N.E.Huang等[4]于1998年提出的一种处理非平稳信号的处理方法。该方法克服了FFT及小波变换的不足,在多个领域(如生物医学、地球物理学等[5,6])都取得了较好的效果。下面,笔者将HHT引入电力系统,用来对电能质量的扰动信号进行检测和定位,并通过MATLAB仿真验证该方法对电力系统非平稳扰动信号检测的效果。
1 HHT变换
HHT由经验模态分解法(Empirical Mode Decomposition,EMD)和Hilbert变换2个关键部分组成,其核心部分为EMD。HHT技术利用EMD对非线性、非平稳信号进行线性和平稳化处理,以此获得固有模态函数分量(Intrinsic Mode Function,IMF),通过利用IMF进行Hilbert变换,获得各个特征分量的瞬时频率和幅值。
1.1EMD
EMD在处理信号过程不受到任何基函数的限制,可以根据信号自身的局部特性,进行特征提取。因此,用EMD处理电能质量的暂态数据,优势较为突出。利用EMD进行暂态扰动信号进行分析,需要满足以下要求[4]:①待检测数据的极值点不低于2个,至少1个极大值,1个极小值;②待检测数据相邻的极大值和极小值的时间间隔,可以唯一确定信号的局部特征;③部分检测数据不满足①的要求,但是存在拐点,也可以进行分解,先利用微分求出数据的极值点,再积分即可。
EMD分解的主要依据是特征时间尺度,根据其大小依次筛选。首先把特征时间尺度最小的取出来,随后原本特征时间尺度较大的分量变为剩余数据中特征时间尺度最小的分量,再对其提取出来,依次类推,最后把特征时间尺度最大的分量取出来。假设待检测的扰动信号为x(t),采用EMD方法通过下面的步骤对任何信号进行分解[7]:
1)找出分析信号x(t)的最大值和最小值;
2)构造最大值分量和最小值分量的包络线,即为上包络线Xmax(t)和下包络线Xmin(t);
3)求解上下包络线的平均值m(t)=[Xmax-Xmin(t)]/2;
4)用原始数据减去包络线的平均值m(t),得到另一新的数据,即h(t)=x(t)-m(t);
5)判断h(t)是否为IMF函数,即h(t)是否满足上述3个条件:如果h(t)是IMF函数,则筛选结束,记为c(t);如果不满足,则把h(t)当做原始检测数据x(t),重复上述工作,依次得到各阶IMF分量,直到所有满足条件的分量全部提取出来,则终止筛选。
6)待检测数据x(t)由n个IMF和一个不能再次分解的剩余量r(t)组成:
(1)
实际筛选过程中,通常采用由“筛选”前后结果的标准差SD来决定迭代次数:
(2)
迭代阈值SD设为0.2~0.3比较合适。
1.2Hilbert变换
Hilbert-Huang变换根据分解信号的特性时间尺度的进行层层解析,将待检测信号分解为n个IMF,进而求得各个IMF分量的瞬时频率和瞬时幅值。对式(1)中的每个ci(t)进行Hilbert变换可以得到:
(3)
构造解析信号:
zi(t)=ci(t)+jHi(t)=ai(t)ejφi(t)
(4)
于是得到幅值函数和相位函数:
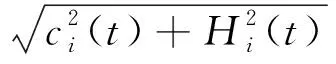
(5)
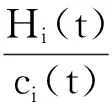
(6)
进一步可以求出瞬时频率:
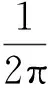
(7)
这样,每个IMF进行Hilbert变换,可得到幅度谱为:

(8)
其中,Re表示取实部;Hilbert边际谱的定义为:
(9)
2 仿真结果与分析
电能质量暂态扰动信号具有随机性强,持续时间短,危害性大的特征,并且产生原因多样化:电网结构、负载类型以及用电环境等都会成为干扰因素,这不仅造成暂态信号检测难度大,还严重影响电力系统的正常运转。针对典型的电能质量扰动信号,笔者参照文献[8~10],采用MATLAB软件生成的扰动信号模型,主要是单一扰动信号模型,包括谐波、电压中断、电压暂升和电压暂降以及以上几种扰动信号结合生成的复合扰动信号模型,利用HHT技术对信号进行检测和定位。谐波是指电网基波的整数倍,谐波容易导致设备老化,寿命缩短,电能计量的不准确性。电力系统的奇数次谐波较为突出,仿真谐波信号是三次谐波和五次谐波。电压中断为一种较短时间内电压缺失的现象,持续时间较短,通常发生在1min以内。电压中断的危害突出,会导致系统故障、用点设备故障或者控制失灵等。
2.1典型单一扰动信号仿真
图1~图3分别为对暂态谐波、电压中断和电压暂降信号进行仿真的图形。由于电压暂升和电压暂降的数据处理过程基本相似,就不给出电压暂升的仿真图形,仿真数据会在表格中给出。
从仿真的图形可看出,对于典型的电压扰动信号,HHT可以自适应的根据扰动信号类型,进行EMD分解,有效提出不同类型的信号特征数据。

图1 谐波信号及其分析结果
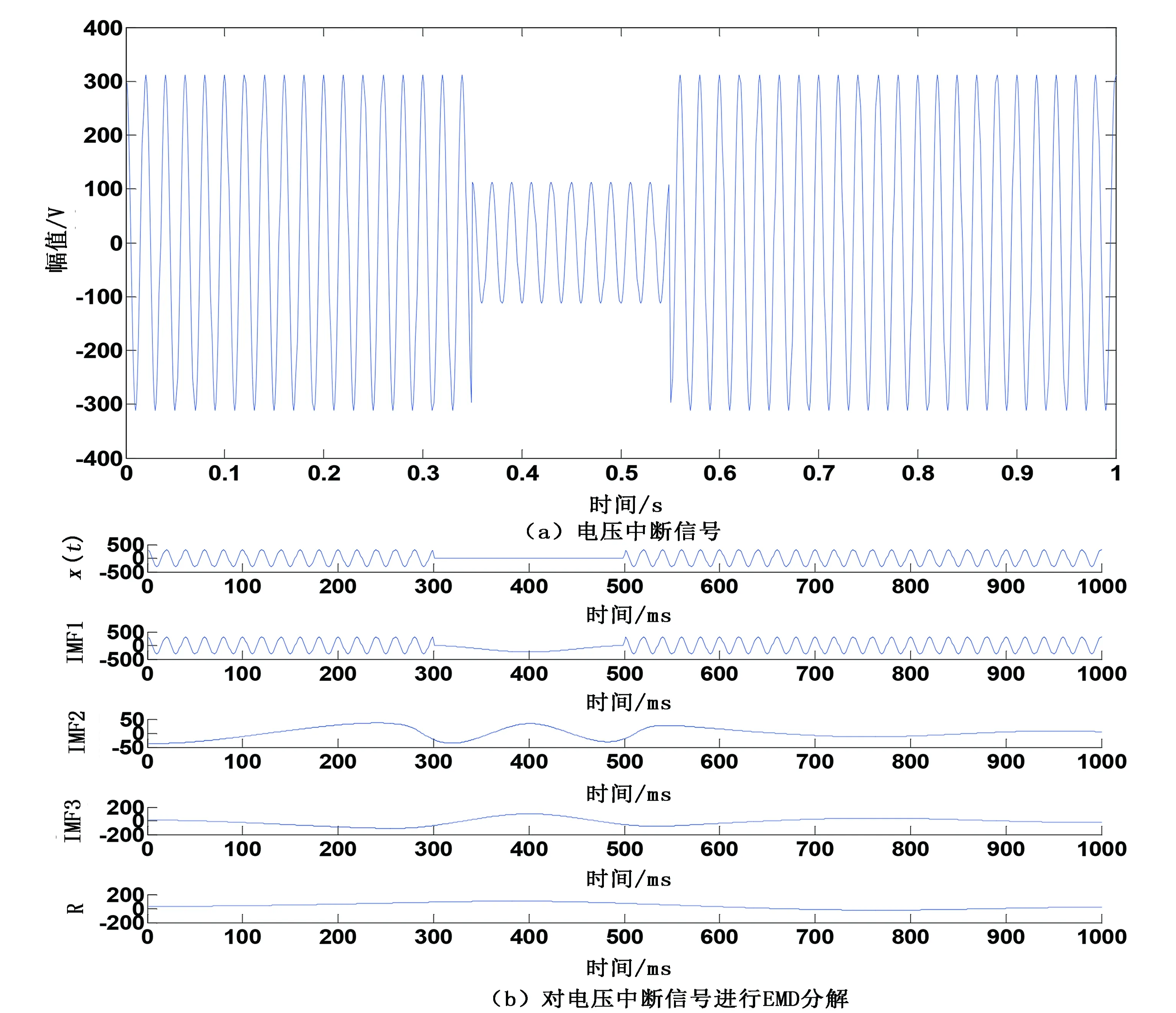
图2 电压中断及其分析结果

图3 电压暂降及其分析结果
2.2单一扰动仿真数据分析
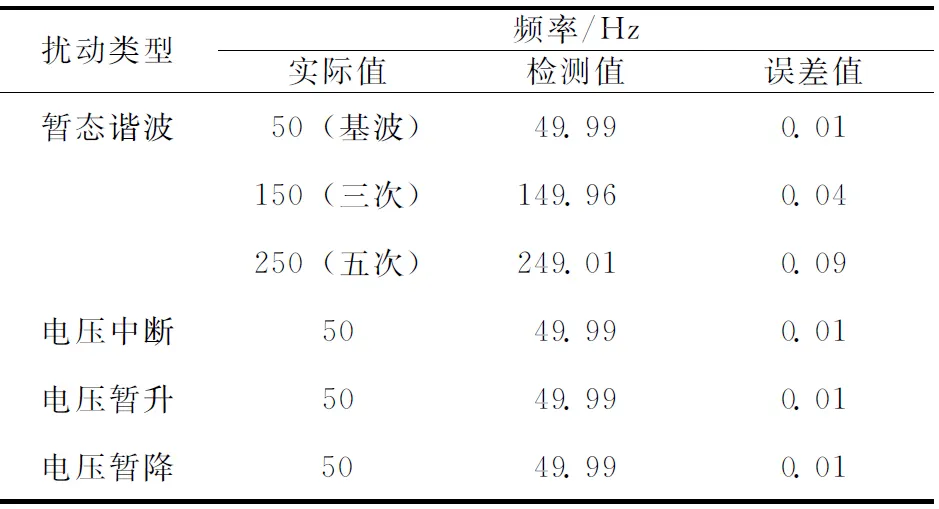
表1给出各种扰动信号的起止时刻,表中的暂态谐波是三次和五次谐波数据。从表1的数据可以得出,HHT可以有效准确检测电能质量暂态信号的起止时刻,检测精度很高,误差都在0.003范围内。表2和表3分别给出了各类数据的幅值和频率数据,误差基本保持在0.04%范围,仅在检测数据中断时,误差相对大一些,一般认为电压降低到0.1倍额定电压以下,就认为是电压中断。利用HHT对电能质量典型的单一扰动信号的检测检测结果较为准确,说明该方法在电力系统可以得到很好应用。
表1HHT起止时刻数据分析

表2HHT幅值数据分析
表3HHT频率数据分析
2.3复杂扰动信号仿真
电力系统的扰动信号除了单一信号形式,还会以复合扰动信号的形式出现。在这里给出了各扰动信号复合的形式,并通过HHT技术进行检测。分别仿真了短暂谐波和间谐波的复合谐波信号(短暂谐波采用的是基波和三次谐波,其中间谐波采用的是52Hz的五次间谐波)、复合中断信号(由基波、三次谐波和中断信号组成)、复合暂降信号(由基波、三次谐波和暂降信号组成),结果如图4~图6所示。由于暂升和暂降信号在数据组成很相似,在这里只给出了仿真数据。
2.4复合扰动仿真数据分析
表3给出复合扰动信号的起止时刻,表4给出复合扰动信号经过HHT处理后信号幅值,表5给出HHT提出的复合信号的频率数据。从表4中可以看出,在复合扰动的起止时刻的计算中,误差跟前面的单一扰动扰动检测的误差相似,保持在0.003的误差范围,检测精度较高。在检测复合信号的幅值过程中,从表5的检测数据可以发现,复合扰动信号的检测精度较单一信号有所下降,其中对复合中断的检测中,误差最大,其他复合扰动的检查基本保持的在10-1数量,在检测误差范围内。
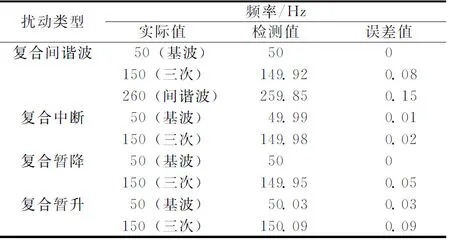
信号的频率检测数据参见表6,在电压中断、暂升和暂降的情况下,无论在复合还是单一的数据处理中,检测数据的精度基本一致。在复合谐波的情况下,融合了基波、三次谐波和五次间谐波,数据显示,间谐波的检测效果相对差一些,误差值为0.15,误差率为0.05%,相对的其他复合信号的误差率也基本保持在一个数量级别上。
通过对单一和复合扰动信号的仿真及其数据分析可以看出,HHT可以有效的对电能质量扰动信号的关键数据进行检测,并且检测数据精度较高,相对复合扰动信号,单一扰动的精度稍微高一些。
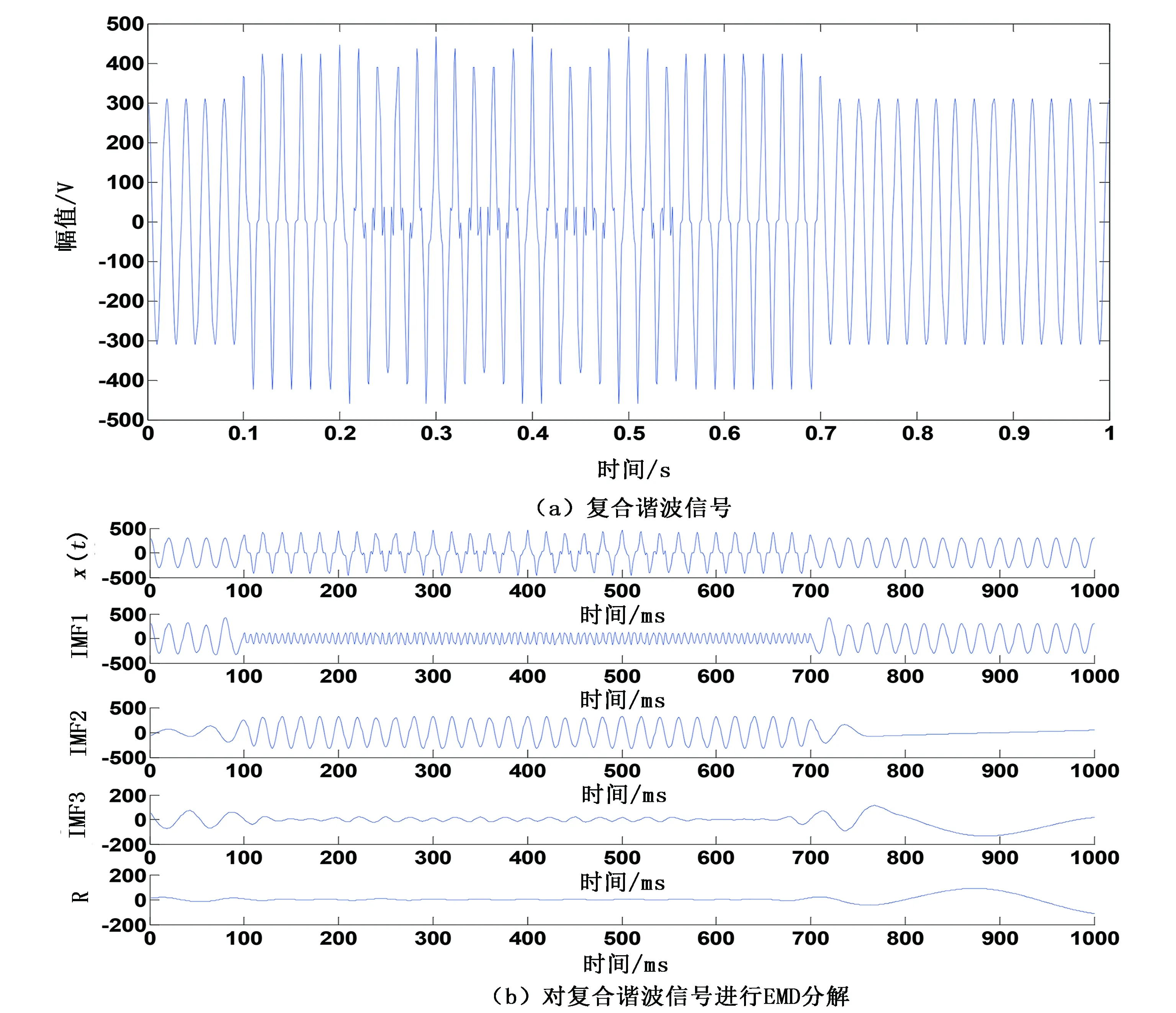
图4 复合谐波仿真结果
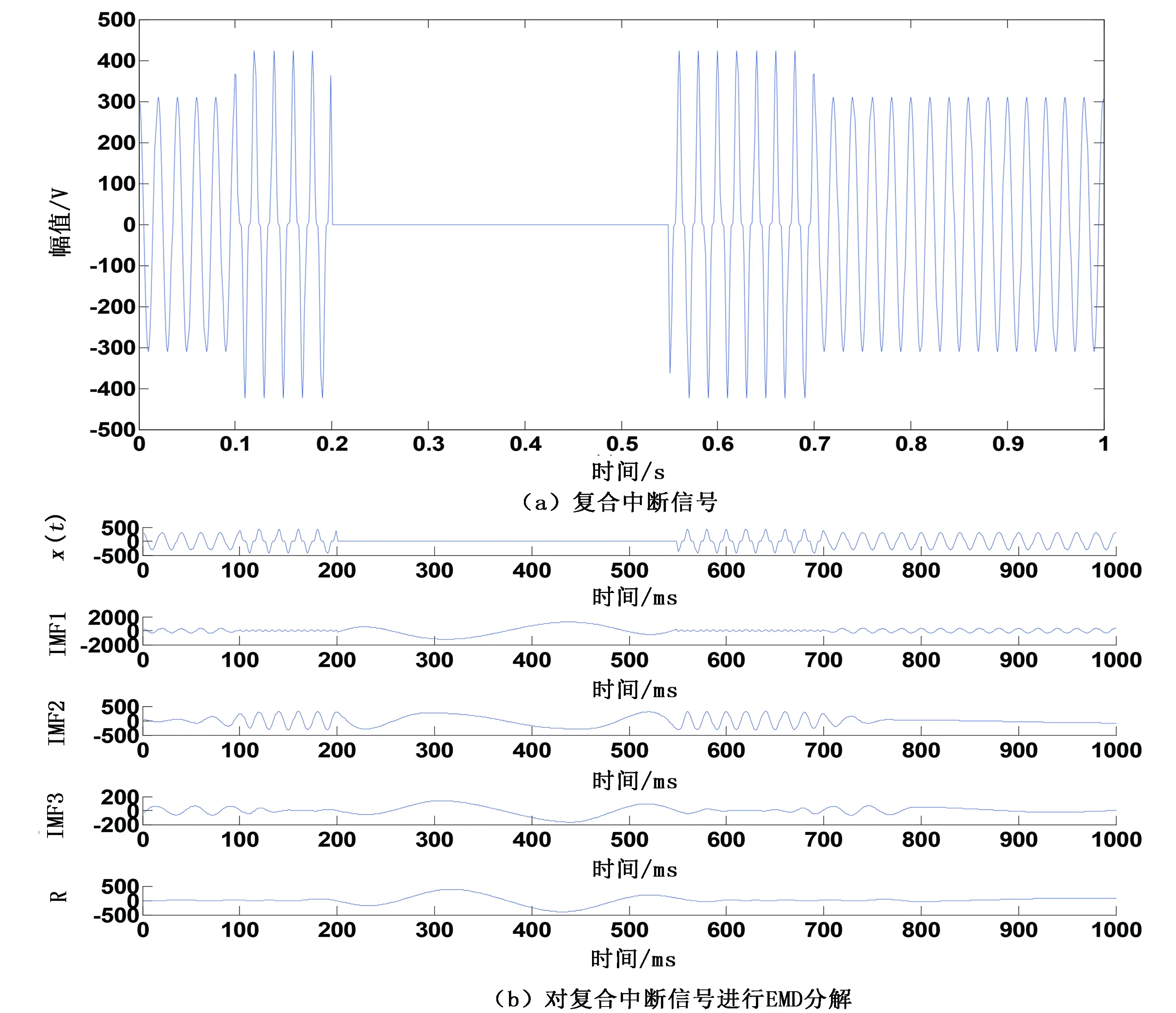
图5 复合中断仿真结果
表4HHT提取复合扰动信号的起止时刻数据分析

表5HHT提取复合扰动信号的幅值数据分析

表6HHT提取复合扰动信号的频率数据分析
3 结论
1)对电能质量典型的扰动信号建立模型,利用HHT对电能质量扰动数据进行分析,分别对暂态谐波、电压中断、电压暂升和电压暂降4类比较典型的暂态扰动及其复合扰动组合信号进行仿真检测。
2)HHT能够比较准确地检测出影响电能质量的典型扰动信号起止时间、频率和幅值信息,并且能达到较为满意的精确度。
3)该验证结果为电能质量的暂态数据的检测提供了新思路,为生产实践和工程应用开辟了新途径。
[1]卡米赛提·拉姆莫汉·饶.快速傅里叶变换:算法与应用[M].北京:机械工业出版社,2016.
[2]Santoso S,Powers J,Grady W M,et al.Power quality assessment via wavelet transform analysis[J].IEEE Transactions on Power Delivery,1996,11(2):924~930.
[3]Angrisni L,Daponte P,Dapuzzo M,et al.A measurement method based on the wavelet transform for power quality analysis[J].IEEE Transactions on Power Delivery,1998,13(4):990~998.
[4]陈娟.Hilbert-Huang变换及其在信号处理中的应用[D].大连:大连理工大学,2006.
[5] Huang W, Shen Z, Huang N E,et al.Use of intrinsic modes in biology: examples of indicial response of pulmonary blood pressure to step hypoxia[J].PNAS,1998(95):12766~12771.
[6]Huang N E,Chern C C,Huang K,et al.A new spectral representation of earthquake data: hilbert spectral analysis of station tcu129 [J].Bulletin of the Seismological Society of America,2001,91(5):1310~1338.
[7]Olhede S,Wald A T.The hilbert spectrum via wavelet projections[J].Proc R Soc A,2004(460):955~975.
[8]Gargoom A M, Ertugrul N, Soong W L. Automatic classification and characterization of power quality events [J]. IEEE Transactions on Power Delivery, 2008, 23(4): 2417~2425.
[9] 张全明, 刘会金. 最小二乘支持向量机在电能质量扰动分类中的应用[J]. 中国电机工程学报, 2008, 28(1): 106~110.
[10] Uyar M, Yildirim S, Gencoglu M T. An expert system based on S-transform and neural network for automatic classification of power quality disturbances [J]. Expert Systems with Applications, 2009, 36: 5962~5975.
[编辑] 洪云飞
TM711
A
1673-1409(2017)17-0053-07
2017-06-18
安徽省高等学校省级质量工程项目(2016jxtd104)。
纪萍(1980-),女,硕士,讲师,现主要从事电力系统信号控制检测处理等方面的教学与研究工作,471374754@qq.com。
[引著格式]纪萍,吴静妹,陈玲.基于HHT的电能质量暂态扰动信号检测技术[J].长江大学学报(自科版),2017,14(17):53~59,80.
