基于数据统计分析的因果关系建模研究

韦咪娜, 袁德成, 庄亚文, 魏志斌

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

基于数据统计分析的因果关系建模研究

韦咪娜, 袁德成, 庄亚文, 魏志斌

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

针对复杂工业过程中变量多、变量间关系复杂、变量关系难以准确量化的特点，提出一种分析变量关联关系及因果关系的数值方法，提高了因果关系分析的计算效率和精度.以TE化工过程模型为研究对象，针对TE流程中生产成本突增的问题，采集回路中控制偏差与生产成本的时间序列数据，建立其局部线性自回归模型,分析多组控制偏差与成本间关联性，运用数值算法计算了时域和频域因果关系.结果表明:反应器压力偏差是TE过程生产成本增加的主要原因，同时得到其他变量间的关联性.通过仿真实例验证了方法的有效性.

因果关系模型； 复杂工业过程； 时间序列数据

基于数据驱动的因果关系建模在大型复杂工业过程的分析和设计中发挥着越来越重要的作用，尤其是在解决系统异常根本原因分析、异常报警管理、全流程控制系统设计方面具有重要应用价值[1].在全流程复杂系统，如现代工业过程、生物系统、社交网络，各变量间互相联系，系统行为取决于每对变量间的相互关系及每一变量的局部动态特性，因此，识别这些关联关系，即关联性与因果关系对于分析系统的影响机制、结构特征和整体动态特性非常重要.连通性和因果关系获取方法有知识驱动和数据驱动两种形式：知识驱动作为一种依据过程知识定性建模的方法，由于对过程知识的完整性要求十分高，因此，并非总是可用；而现代化工业企业每天运行在DCS数据库中，积累了大量数据，为建模及分析提供了宝贵资源，因此，建立基于数据驱动的拓扑结构，构建因果关系网络更加实用可行，这已成为学术界和工业界关注的重点.

针对过程变量，探测因果关系的数据驱动方法分为三类：滞后模型法(包括格兰杰因果关系、传递熵)、条件独立法(贝叶斯学习)、高阶统计量法.Duan P等运用传递熵测定有向因果关系[2]，虽然传递熵法无模型、无线性限制，但存在过渡依赖PDFs(工艺物料平衡图)，增大了计算负担，时间滞后无法估计，且易受非平稳噪声影响.Baucer M等运用互相关分析识别厂级干扰传播路径，通过建立CCF(互相关函数)弥补了传递熵法无法估计时间滞后的不足[3]，其计算方便，但忽视了时间序列趋势，所得时间滞后仅为估计值，计算精度仍有待改进.Cowell R G等通过贝叶斯学习建立随机网络及专家系统[4]，尽管循环因果关系算法的开发弥补了传统贝叶斯网络无环图在获取系统动态特征中的不足，但模型的建立需要所有模式下的数据，甚至包括所有故障模式下的数据，成为建立贝叶斯网络的最大限制.

本文通过建立时间序列数据的多变量的向量自回归模型(VAR)进行格兰杰因果分析(Granger Causality Analysis)，在时域分析的基础上，对因果影响进行谱分解，对多元自回归过程的分解使得因果关系的谱表示更加明确有效，采用数值算法建立VAR模型，精确估计了模型的阶与滞后系数，在时间序列数据长度足够的情况下可检测到变量间微弱相关关系，并在可接受计算负担内提高了计算效率和精度.实验仿真证明了本文运用数值途径实现格兰杰因果分析方法的有效性.

1 数据获取与处理

美国Tennesses Eastman化工公司在实践基础上研究出了一个可进行控制方案设计、控制策略研究的仿实际过程的工业模拟模型，即TE化工过程模型.TE过程模型变量多，变量关系复杂，且连续系统中各单元间有较强的相互作用，是一个典型的复杂多约束非线性过程[5].本文选取TE过程9个控制回路的控制偏差与生产成本共10个变量为研究对象，在TE过程的simulink模型中加入随机干扰，进行3次试验，运行TE仿真模型采样，得到维数为3×1 000×10的数据，即10个过程变量的时间序列.

基于数据分析的因果关系建模对序列的稳定性非常敏感，非平稳时间序列的因果关系检验会得到伪回归，导致产生虚假因果关系[6].因此，在进行因果关系建模前，需对采集到的数据进行平稳性检验.对于时间序列Xt可通过下式进行平稳性检验：

(1)

ΔXt为t时刻序列数据变化量，δ为时间序列系数，εt表示噪声序列.原假设和备择假设为H0:δ≥0;H1:δ<0;通过t统计检验量进行检验，当t统计量小于τ，拒绝原假设H0，Xt序列平稳；若t统计量大于τ，则接受原假设，认为Xt存在单位根，为非平稳序列.如果序列为非平稳序列，接下来继续检测ΔXt的平稳性，直至检验结论表明差分后的序列为平稳序列为止.

2 因果模型建立

2.1 VAR模型的建立

建立向量自回归模型(VAR)是目前研究变量间格兰杰因果关系的主要方法.针对两个随机过程Xt和Yt，可分别建立它们的VAR模型：

(2)

(3)

单变量向量自回归模型反映了随机过程当前值与过去值之间的关系，方差Σ1或Γ1表明这种预报关系的正确程度.也可建立两个随机过程间的联合回归模型，反映两随机过程间的关联性.

(4)

(5)

其中噪声误差项在时间上不相关，在同一时刻的自相关矩阵定义为:

(6)

式中:Σ2=var(ε2t),Γ2=var(η2t),如果Xt与Yt不相关，则{b2j}和{c2j}等于零，γ2=cov(ε2t,η2t)等于零，Γ2=Γ1.

在复杂系统中，并非总是仅存在两变量关系，无约束回归将导致虚假因果关系的产生.当随机过程Yt与Xt间不存在直接因果关系，但Xt、Yt都与随机过程Zt存在滞后相关关系时，无约束回归将会错误地预报Xt、Yt间的因果关系[7].在此情况下，建立3变量间的有约束回归模型将会有效消除因果推断中一些变量可能造成的混杂影响.对于3个随机过程Xt、Yt和Zt，先建立Xt和Zt之间的VAR模型：

(7)

(8)

式中协方差矩阵为：

(9)

进一步加入第3个随机过程Yt，建立3个过程间的VAR模型：

ε4t, var(ε4t)=Σxx

(10)

η4t, var(η4t)=Σyy

(11)

χ4t, var(χ4t)=Σzz

(12)

其中，协方差矩阵

(13)

当Yt与Xt间的因果关系可以完全由Zt间接表达时，{b4j}为零矩阵，Σ3=Σxx，则在Zt约束下，Yt对Xt的因果关系为零，加入随机过程Yt的过去值对Xt的预测效果没有改善.另一方面，如果Yt对Xt存在直接影响，加入Yt的过去值将会更好地预测Xt值，Σ3>Σxx，存在在Zt约束下Yt对Xt的因果关系[8].

对于所建立的VAR模型，运用杜宾-瓦特森(Durbin-Watson)统计量检测回归分析中的残差项是否存在自相关.根据模型估计数据预测时间序列趋势，与实际数据对比，检验模型一致性.

2.2 时域格兰杰因果关系分析

两个随机过程Xt和Yt之间的总体相关性为：

(14)

Σ表示封闭(有限项)矩阵的行列式，Σ1或Γ1分别为两随机过程方差.当两个时间序列Xt和Yt不相关时，它们的总体互相关性FX,Y=0成立；反之，则有FX,Y>0.参照式(2)、(4),如果Σ2小于Σ1，则可以判断加入Yt的过去项后Xt预报更加精确，也可以认为Yt对Xt因果影响.它们之间的这类因果影响关系为：

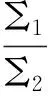
(15)

如果FX→Y等于零，从Yt到Xt没有因果关联；如果FX→Y大于零，则存在相互影响.类似地，Xt到Yt的因果关联如下：

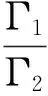
(16)

Xt到Yt的间接相关性：

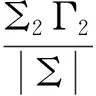
(17)

如果γ2=cov(ε2t,η2t)等于零，则FX,Y等于零；反之，FX,Y大于零.根据以上定义，两变量之间的因果关系可以统一在一个公式中：

FX,Y=FX→Y+FY→X+FX·Y

(18)

引入第3个变量后，可能存在直接和间接的关联，如图1所示.

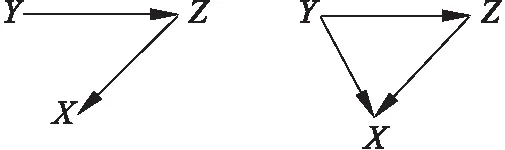
图1 三变量因果关系

经过Zt传递的、从Yt到Xt的因果关联为：

(19)

2.3 频域格兰杰因果关系分析

格兰杰因果关系具有将因果关系进行相应频域分解的突出优势，能够清晰反映两个随机过程产生关联的频率[10].频域分解得到的谱因果分析整合了时域的因果关系，可认为是所有频率谱因果关系的平均值.随机过程Xt、Yt频域分解的谱因果关系为:

fY→X(λ)≡

(20)

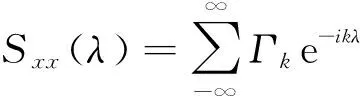
Sxx(λ)=Hxx(λ)Σxx(λ)Hxx(λ)*+

Hxy(λ)Σyy(λ)Hxy(λ)*

(21)

偏协方差矩阵：

Σy|x≡Σyy-ΣyxΣxx-1Σxy

进一步针对3个随机过程Xt、Yt、Zt建立频域内受约束回归模型.先建立Xt、Zt间VAR模型：

(22)

(23)

X*、Z*为白噪声残差，其与随机过程Xt的转换如下:

(24)

则频域内3个随机过程的有约束的谱因果关系为

fY→XZ(λ)≡fY⊕Z*→X*(λ)

(25)

3 实验仿真

3.1 VAR模型参数

VAR模型参数：模型阶数为7阶，滞后系数5 975，谱半径 0.996 922，相对误差3.279 9×10-11，时域与频域因果关系最大相对误差9.68×10-12<1×10-5.模型一致性100 %.杜宾-瓦特森统计检测(D-W检验)结果见表1.

表1 VAR模型D-W统计检验

可以看出变量残差在0.05的显著性水平上不存在自相关.修正后的R2基本大于90 %，模型拟合良好.

3.2 因果关系仿真结果

格兰杰因果关系及显著性分析如图2、图3所示.

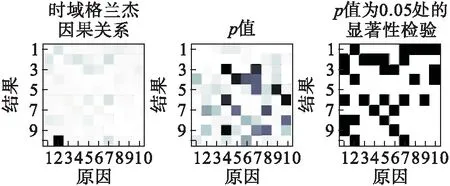
图2 时域格兰杰因果关系

图3 格兰杰因果关系显著性检验

从图2可以看出：在时域内建立10维时间序列数据的多约束自回归模型，变量2→10存在明显格兰杰因果关系，其次变量7→10、7→6、7→2 等也存在单向关联性.相应地，这些因果关系或关联关系在网格图中显示P值检验极小，显著性检验结果显著，验证了格兰杰因果关系分析结果的可靠性.在图3中，进一步对回归模型中每对关联关系显著性进行了理论检验与置换检验.置换检验作为基于计算机的模拟方法，不依赖原始数据分布，以两样本均数之差作为统计量，充分利用样本数据信息，提高了检验效能并再次验证了所得因果关系.

在时域因果关系分析的基础上，编写格兰杰因果分析算法程序,将随机过程进行谱分解，变换时域中VAR模型参数为频域中新变量，并根据式(25)计算谱因果关系.分析10组随机过程变量在GC(Granger Causality)因果关系最大的频率点上的格兰杰因果关系连接，发现10组时间序列数据两两配对因果关系呈现出明显峰值，在10 Hz频率点附近变量2→10、7→10、7→6之间的单向因果关系显著，仿真结果如图4所示.从图4与图5可以看出：变量2(反应器压力偏差)与7(汽提塔出流量控制偏差)对10有直接作用，变量3与2、7与2等存在微弱的相关关系.

图4 谱因果关系

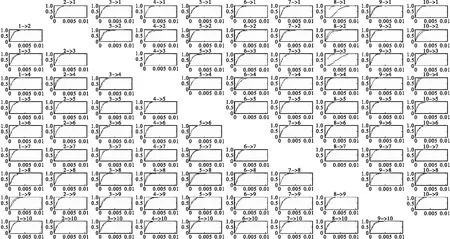
图5 零分布的K-S检验图

变量间关联关系见图6.置换检验结果表明所得谱因果关系是显著的，进一步证实了反应器压力偏差、汽提塔出流量控制偏差这两个变量与生产成本间的单向因果关系.TE过程的经济消耗主要由原料消耗、放空气体中残留产品和原料及处理F产品的消耗组成，反应器压力控制偏差可直接影响物料反应速率与转化率，未完全转化原料的流失会增加经济消耗，因此，反应器压力控制偏差与生产耗费间的因果关系不违背实际生产情况，这也与以上时域因果分析的结果一致.

图6 变量间关联关系

3.3 仿真验证

运行仿真系统，验证反应器压力的测量值与生产成本之间因果关系，如图7、图8所示.

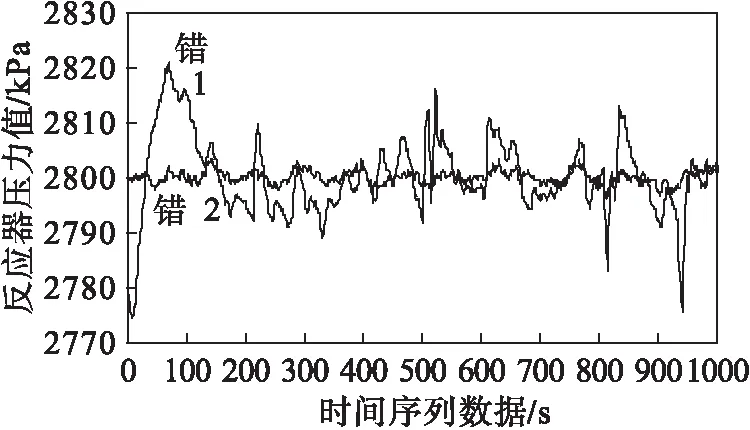
图7 反应器压力图

图8 TE过程生产成本图

其中图7中横坐标为样本时间序列数据，采样单位为s，纵坐标表示反应器压力值，单位为kPa；图8中横坐标为样本时间序列数据，采样单位为s，纵坐标表示生产成本值，单位为万元/最大生产率.

图7与图8中曲线1和曲线2分别为第一次、第二次实验测量值，两次实验中反应器压力设定值均为2 800 kPa.当反应器压力偏离设定值，生产成本随之增加，并且偏差越大，成本增加越多.反应器压力偏差在接近第100个采样单位处达到最大，生产成本在第100个采样单位后亦达到最大值.观察图7、图8可得反应器压力偏差与生产成本的强因果关系，并存在约0.5个单位时间的滞后，验证了该方法的有效性.

4 结 论

建立了时间序列数据的VAR模型，运用数值算法实现对多变量关联性及因果关系的分析.得出时域和频域中因果关系，两者最大绝对误差9.68×10-12，分析结果基本一致.运用数值解法计算变量因果关系，提高了计算效率和计算精度，可以解决统计不准确和计算效率低的常见问题.仿真验证表明：存在反应器压力偏差与生产成本间的因果关系，证明了该方法的正确性.

[1] YANG F,SHAH S,XIAO D Y.Signed Directed Graph based Modeling and its Validation from Process Knowledge and Process Data[J].Int J App Math Comput Sci,2012,22(1):41-53.

[2] DUAN P,YANG F,CHEN T，et al.Direct Causality Detection via the Transfer Entropy Approach[J].IEEE Trans Control Syst Technology,2013,21(6):2052-2066.

[3] BAUER M,THORNHILL N F.A Practical Method for Identifying the Propagation Path of Plant-wide Disturbances[J].J Process Control,2008,18(7):707-719.

[4] COWELL R G,DAWID A P,LAURITZEN S L.Probabilistic Networks and Expert Systems[J].Springer-verlag,1999,39(20):2548-2558.

[5] 袁德成.过程控制工程[M].北京：机械工业出版社，2013：13-21.

[6] OYELEYE O O,KRAMER M A.Qualitative Simulation of Chemical Process Systems:Steady-State Analysis[J].AICHE J,1988,34(9):1441-1454.

[7] YANG F,XIAO D Y.Review of SDG Modeling and its Application[J].Control Theory & Applications,2005,22(5):767-774.

[8] SETH A K.A Matlab Toolbox for Granger Causal Connectivity Analysis[J].J Neurosci Methods,2010,186(2):262-273.

[9] YIM S Y,ANANTHAKUMAR H G,BENABBAS L,et al.Using Process Topology in Plant-wide Control Loop Performance Assessment[J].Comput Chem Eng,2006,31(2):86-99.

[10] GRANGER C W J.Investigating Causal Relations by Econometric Models and Cross-spectral Methods[J].Econometric,1969,37(3):424-438.

Abstract: A great number of process variables existed in the complex industrial process.The relationship between these variables were complicated and very difficult to quantify accurately.A numerical method of analyzing the variable relationship and causality was put forward aimed at improving the calculation efficiency and precision.Focus on TE process model,a great deal of time series data of control deviation and production cost was collected to establish their local linear auto regression model,in order to interpret the soaring production cost.Connectivity among these variables was discussed and some numerical algorithm was adopted to compute causality relationship in both time domain and frequency domain.The result showed that the reactor pressure deviation is the main cause of the raise of the cost of TE production process.Simultaneously,the connectivity and correlation of other variables were captured.The simulation validated this method was correct and effective.

Keywords: causal model; complex industrial process; time series data

StudyontheCausalModelingBasedonStatisticalAnalysisofData

WEI Mi-na， YUAN De-cheng， ZHUANG Ya-wen， WEI Zhi-bin

(Shenyang University of Chemical Technology, Shenyang 110142， China)

10.3969/j.issn.2095-2198.2017.03.015

TP1

A

2015-03-24

韦咪娜(1989-)，女，河南洛阳人，硕士研究生在读，主要从事数据驱动、统计分析等方面的研究.

袁德成(1960-)，男，内蒙古阿拉善人，教授，博士，主要从事化工过程建模、控制与优化的研究.

2095-2198(2017)03-0266-07