一类非线性广义生物经济系统的保性能分析

张 翼， 赵慧颖

(沈阳工业大学 理学院， 辽宁 沈阳 110870)

一类非线性广义生物经济系统的保性能分析

张 翼， 赵慧颖

(沈阳工业大学 理学院， 辽宁 沈阳 110870)

研究一类非线性广义生物经济系统的保性能控制问题.考虑到外来物种对原产地鱼类种群的影响，首先,从人工捕获收益、对外来物种的净化能力和捕捞鱼类年龄段因素入手，建立非线性广义生物模型，讨论系统平衡点，将T-S模糊方法转化为线性模型去研究；其次，在此基础上设定加入满足Lipschitz条件的扰动项，用LMI方法给出一个简化的非线性不确定广义模型保性能控制器存在的条件，满足相应的保性能指标；最后，使用数例仿真验证了研究结果的有效性.

广义系统； 生物经济系统； 不确定； 保性能； T-S模糊系统

国际旅游业和全球经济贸易的发展，加速了物种的自然入侵和迁徙.一些动植物正在通过人类有意或无意的行为，被引入到其他的环境中，大家有目共睹的是这些入侵者损害了当地的生态系统和地理结构， 给原产地生物和居民造成了不良影响.我国是遭受生物入侵最严重的国家之一，生物入侵形势十分严峻.目前，入侵中国的外来物种已达540多种，其中有超过100种物种造成当地生态系统的大面积严重损害.根据农业部的最新统计， 近年来，外来物种一直在中国呈不健康的发展趋势，随着被引入数量的增加，传播速度的加快，传染程度的扩大，其危害不断加剧，对我国的生态环境造成严重的影响.本文旨在用广义系统理论探讨一些相关问题.

广义系统广泛用于描述一些实用系统，目前已应用到各个领域，例如在电子网络、动力系统、航天船舶、生物化学研究等方面，并取得了很多研究成果[1-5].关于外来物种入侵，文献[6]提出了一个广义生物经济模型，研究了基于广义系统和分岔理论的外来物种入侵下的单种群鱼类Logistic模型，考虑加入净化能力，设计了状态反馈控制器，旨在消除预期外的奇异诱导分岔.文献[7]研究的是生物经济广义马尔科夫跳变系统的模糊随机优化保性能控制，设计了模糊状态反馈控制器，给出严格线性矩阵不等式证明.

在广义系统控制器设计中，实现相关的鲁棒性和系统稳定性是非常重要的.不确定线性或非线性系统的保性能控制理论，在过去的几十年中已经得到广泛应用[8-10]，其中鲁棒控制是一种对非线性广义系统普遍适用的控制方法，而著名的Takagi-Sugeno(T-S)模糊模型也是处理复杂非线性系统的一个方便的工具.研究表明：用T-S 模糊模型描述的非线性系统的综合问题可简化为涉及到线性矩阵不等式(LMI)的凸问题，用T-S模糊模型线性化的方法广泛用于许多非线性系统的研究中[11-13].

本文以Logistic增长模型为基础，结合Lotka-Volterra 模型[14-15]，考虑要捕捞的鱼类种群分阶段结构，且只捕获成年鱼群，加上外来物种的影响，以及对入侵物种的人为净化能力，建立广义生物模型.通过给出模型的稳定性分析和T-S模糊线性化方法，得到简化的线性系统模型.考虑到鱼类种群的生存还受到自然因素的影响，加入了适当的扰动项，本文只考虑了模型中的扰动项满足Lipschitz条件的情况.应用LMI方法给出保性能控制器存在的条件，使闭环系统满足广义二次稳定，保性能函数有上界.仿真实例验证了研究结果的有效性.

1 预备知识和建立模型

1.1 相关生物模型

(1) Logistic模型

Logistic模型是研究种群生长的重要理论，可描述种群S型增长：

(1)

这里N(t)表示t时刻的种群数量；r是内禀增长率；K是环境承载量.

(2) Lotka-Volterra模型

在很多案例中，来自同一生态系统的所有物种和它们之间的相互作用需要作为一个整体纳入考虑，多种群的生物增长模型中提出了Lotka-Volterra模型：

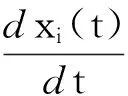
i=1,2,…,n

(2)

它代表了一个n种群生态系统，xi(t)是第i个种群在t时刻的数量；ai(t)∈R是第i种群的内禀增长率；bi≥0是第i个种群的种内制约率；当j≠i时，cij是第i种群和第j种群的种间制约率.

(3) 阶段结构模型

当只考虑一个单一的鱼类种群，它们的生命过程可以被划分为两个阶段，即幼年阶段和成年阶段.在相同的阶段，每个个体有完全相同的生物学特征，因此，在某种程度上，鱼类种群的最重要的比率与阶段结构有很大关系，例如增长率、生育率、死亡率.

一个分阶段结构的单种群生物模型可写作下列形式：

(3)

这里xi(t)(i=1,2)分别表示幼年和成年鱼群的密度；r是幼年鱼群的出生率；ai(i=1,2)分别表示幼年和成年鱼群的死亡率；b是幼年鱼群到成年的转化率；ci(i=1,2)分别表示幼年和成年鱼群的密度制约系数.

1.2 建立模型

模型的研究背景是在外来物种与原产地鱼类种群存在竞争关系的前提下，在入侵物种与本地鱼群构成的生态系统中，参考渔业捕获行为及人类对入侵物种有净化行为，同时把本地鱼群分阶段结构.考虑到渔业的发展，假定渔业捕捞主要捕获本地成年鱼群，幼年鱼群被捕获后大多被放生，因此，作为经济产品的幼年鱼群数量远小于成年鱼群，可忽略不计.然后在生存条件一定的情况下，不受外界因素制约，外来物种前期对于新的适宜环境有急速增长的趋势，假定鱼群对外来物种的竞争作用远小于外来物种对鱼群的竞争作用，把外来物种竞争死亡的影响归入自身死亡率中，在此基础上研究外来物种入侵下的本地鱼群系统的动态学行为.本文模型在本地种群分阶段结构的基础上，着重加入外来物种的人工净化，讨论保性能问题.

根据Gordon经济理论[16]： 可持续经济收益=可持续总收益-可持续总成本， 当给定捕获量H， 即：

H(t)(x(t)p-c)=m(t)

(4)

其中：p是市场价格；c是单位成本；m(t)是经济净收益.

基于以上考虑，结合(3)式、(4)式， 给出前述背景下的广义生物经济模型：

(5)

其中：xi(t)(i=1,2)分别为幼年和成年鱼群的密度；r是幼年鱼群的出生率；ai(i=1,2)分别表示幼年和成年鱼群的死亡率；b是幼年鱼群变为成年的转化率；ci(i=1,2)分别表示幼年和成年鱼群的密度制约系数；H(t)是t时刻对成年鱼群的捕获量；η表示入侵物种对成年鱼类的制约率；y(t)是外来物种密度；α是入侵物种的自然生长率；a3是入侵物种的死亡率；P(t)是t时刻对入侵物种的净化量；hP(t)是人为对外来物种的实际净化量；βy(t)是目标净化量；μx2(t)代表根据成年种群量做出的调整净化量；ωP(t)是受单位净化成本约束的净化量.

2 平衡点分析和T-S模糊线性化

2.1 平衡点分析

对系统模型进行T-S模糊线性化过程中，需要对模型进行有关平衡点的参数转化，于是在此先对系统的平衡点进行分析.根据文献[16]中的经济理论，当经济净收益为零(m=0)时，出现一个收支平衡，此现象称为经济过度捕捞，是我们不想看到的结果.因此，政府部门应该采取措施控制鱼群捕捞，使系统能持续发展，并获得持续收益.

对于系统(5)，当m=0时，系统(5)有4个平衡点，但只有2个可能的正平衡点：

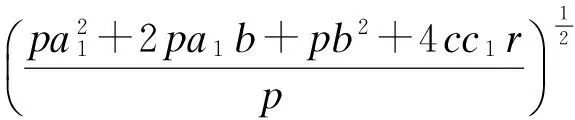
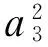
2c2a3cβhwp-2a2a3αw2p2+2a2a3βhwp2+

ηc2h2μ2+c2cα2w2p-2c2cαβhwp+c2cβ2h2p+

a2α2w2p2-2a2αβhwp2+a2β2h2p2)·

(a3wp+βhp-αkp)-2

接下来将讨论系统(5)的稳定性.

(6)

系统(5)是稳定的.

a1+b+ξ1<0,ξ2>0,ξ3>0,

a1+b-ξ1<0,ξ2>0,ξ3>0,

由模型(5)可得:

则在P*点的特征方程为

det(λI-JP)|P*=

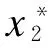
(7)

从上面结果中可以看出λ=0是一个实根，且有2个根取决于下列方程：

λ2+(w-α+a3)λ-wα+wa3=0，

另外2个取决于方程：

所以当满足下列条件：

w-α+a3>0，-wα+wa3>0，

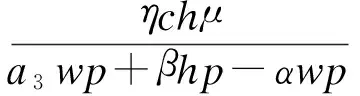
方程(7)的其余4个根都有负实部，模型(5)稳定.

2.2 T-S模糊线性化

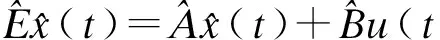
(8)

考虑到种群密度的饱和情况， 可以假定ζ1(t)∈[-l1,l1],ζ2(t)∈[-l2,l2],l1>0,l2>0,并有如下模糊规则：

其中：

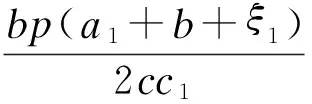
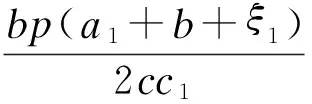
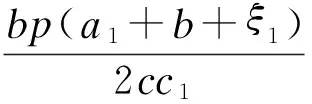
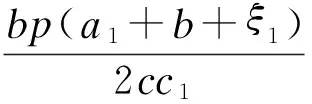
ηξ2+c2l2

于是得到了系统(8)的线性化模型：

(9)

Mij(ζj(t))是ζj(t)在模糊集Mij的隶属度，ψi(ζ(t))≥0(i=1,2,3,4).

3 保性能控制

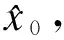
(10)

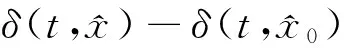
(11)

且有δ(t,0)=0, ∀t≥0,

(12)

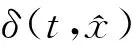
(13)

则(10)是零解渐近稳定的，δ是Lipschitz连续的，式(13)可改写为：

则ΓTΓ≤I.

(14)

且对满足式(11)、式(12)条件的δ有：

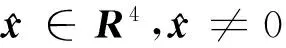
(15)

选取二次型保性能函数为：

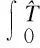
(16)

其中Q、R为正定矩阵，选取状态反馈控制器为：

(17)

(18)

定义2[19]： 系统(10)如果存在状态反馈控制器(17)和正数J*， 使得对所有容许的δ， 闭环系统(18)都是广义二次稳定的， 且性能指标(16)满足J≤J*， 则相应的控制器(17)为系统(10)的保性能控制器.

引理1[19]：对所有容许的扰动， 下列条件等价：

(2) 存在矩阵P满足式(14)、式(15)；

证明： 若闭环系统(18)广义二次稳定，当且仅当

(19)

证明： 由计算可知(19)等价于

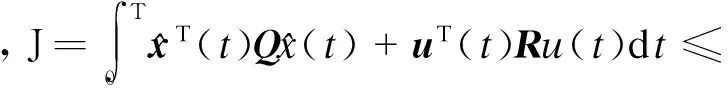
4 数例仿真

以外来物种水花生为例进行研究，其学名是空心莲子草(Mart)，属于苋科.它起源于美国南部和世界的温带、亚热带地区.1892年，他们开始出现在上海附近的岛屿上.上世纪50年代，它们作为猪饲料被饲养和培养，但后来又逃逸到陆地上.近年来，它们在中国遍布黄河流域的大部分南部地区，天津目前也发现这种归化植物.

主要危害：(1)阻塞航道、影响水上交通；(2)挤出其他植物，使物种单一化；(3)覆盖水面， 影响鱼类和渔业的增长；(4)破坏农田作物，减少了他们的产量；(5)在田间沟影响农田灌溉和排水；(6)入侵湿地、草坪，破坏景观；(7)养殖苍蝇，危害人体健康.

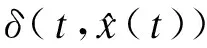
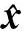
其中：

r=0.2,a1=0.05,b=0.2,c1=0.05,a2=0.03,c2=0.05,η=0.01,α=0.55,a3=0.5,h=0.03,β=1.5,u=0.02,w=0.1,p=4,c=1,m=0，把参数代入模型，有

仿真结果如图1所示.

图1为幼年鱼群量x1(t)、成年鱼群量x2(t)、水花生数目y(t)及对其净化量P(t)和鱼群捕获量H(t)关于时间变化的函数响应图.

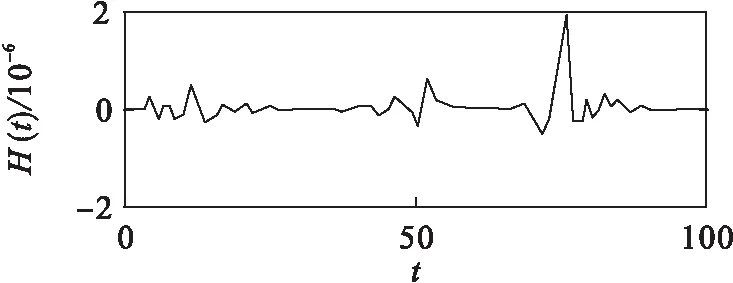
图1 初始数据下的生态系统的生物量及捕获

从图1可看出：各个种群的数量和捕获量之间存在一定量关系，幼年鱼群量增长，成年鱼群量随之增长，净化能力也出现不稳定变化，水花生数量上涨时，鱼群数量呈现减少趋势，人为净化量增加；然后水花生数量下降，鱼群量又开始递增，人为净化量降低.时间在70～80区间内时，捕获量H(t)有较大波动，有个顶峰值，进而产生的附带结果是此区间的鱼群量减少，在时间处于70-80之前捕获程度变化不大，整体系统处于不稳定状态.

实施适当的保性能控制后，对系统进行仿真，结果如图2所示.

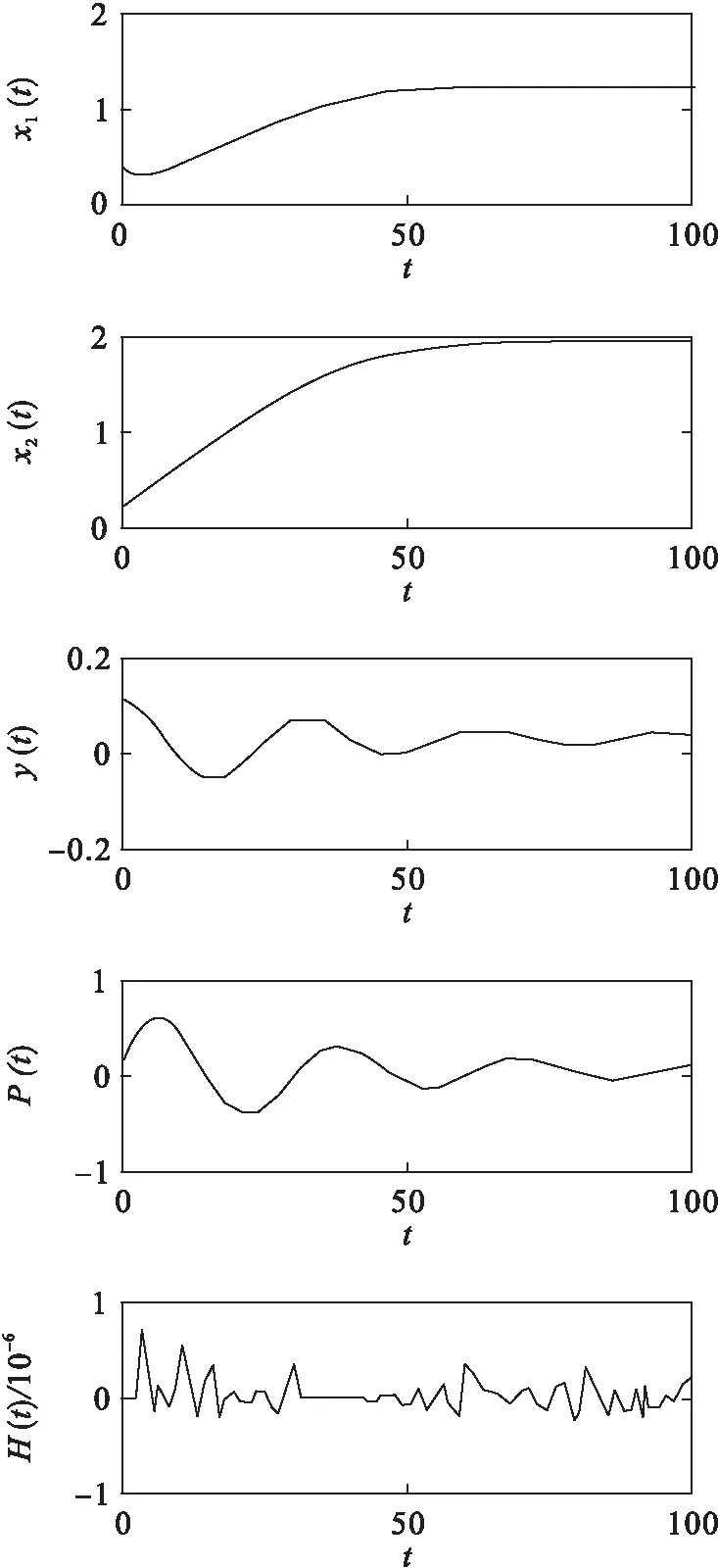
图2 加入反馈控制后的生态系统的生物量及捕获

图2中幼年鱼群和成年鱼群随时间的推移，种群数量良好发展并趋于稳定，水花生数量得到控制，变化幅度减小趋于稳定，人工净化能力也随之减小并趋于稳定，捕获量在一定范围内有序变化，呈健康状态，整体系统随时间推移趋于良好稳定状态.

通过仿真图可清晰地了解原系统在外来物种入侵下的动态反应，随时间推移，系统越来越不稳定，并不利于渔业的发展；而从控制后的仿真图可见：通过调整，捕获量系统随时间推移趋于稳定，鱼群的数量在一定范围内良性增长，利于渔业的发展.

5 结 论

讨论一类有关外来物种入侵鱼类种群的非线性广义经济系统.考虑幼年鱼群在转化到成年鱼群过程中受外界因素影响会出现死亡，有一定的转化率，且不同年龄段的鱼群作为经济产品的捕获情况不同，因此，为了研究外来物种对原产地种群年龄段数量的影响，首先，基于之前的生物模型，给出本文的非线性生物广义模型，并对模型中关于对外来物种的净化能力给出不同的解释；其次，使用了T-S模糊线性化方法，并对自然因素产生的外界扰动，只考虑了满足Lipschitz条件且给定初值条件的情况，得到性能指标公式，并给出保性能控制器存在的条件.本文虽对复杂的生态系统做了动态分析，进一步了解了外来物种入侵系统的一些性能，但研究工作尚待完善，其应用方面还有待进一步研究.

[1] 甘德强，刘佳宇，徐开，等.广义相位补偿法在接入双馈风机电力系统的稳定器设计中的应用[J].高电压技术，2015，41(3)：709-715.

[2] 章雅纯，陈树勇，刘道伟，等.基于映射广义弹性系数的电网静态稳定快速评估判据[J].中国电机工程学报，2015，35(16)：4094-4101.

[3] 刘胜，程垠钟.基于多维gPC的船舶电力推进系统仿真不确定性分析[J].电工技术学报，2016， 31(2)：128-135.

[4] 付江月，陈刚.城市物流网络演化模型与算法[J].计算机工程与应用，2015，51(15)：17-21.

[5] 彭波，李翰林，卢本卓.生物分子模拟中的静电计算[J].计算物理，2015，32(2)：127-159.

[6] ZHANG Y,ZHANG Q L,LI J H,et al.The Bifurcation and Control of a Single-species Fish Population Logistic Model with the Invasion of Alien Species [J].Discrete Dynamics in Nature and Society,2014(32):1-11.

[7] LI L,ZHANG Q L,ZHU B Y.Fuzzy Stochastic Optimal Guaranteed Cost Control of Bio-economic Singular Markovian Jump Systems[J].IEEE Transactions on Cybernetics,2015,45(11):2512-2521.

[8] 邱占芝，张庆灵，刘明.不确定时延输出反馈网络化系统保性能控制[J].控制理论与应用，2007， 24(2)：274-278.

[9] 唐斌，刘国平，桂卫华.不确定系统的网络化保性能控制[J].控制理论与应用，2008，25(1)：105-110.

[10] 杨坤，沈艳霞，纪志成.不确定时变时滞切换广义系统的鲁棒H_∞保性能控制[J].控制与决策， 2013，28(5)：787-790.

[11] 刘文龙.基于T-S模糊模型的多变量非线性预测控制[J].电子测量与仪器学报，2013，27(10)： 998-1003.

[12] 肖会芹，何勇，吴敏，等.基于T-S模糊模型非线性网络控制系统改进H_∞跟踪控制[J].控制理论与应用，2012，29(1)：71-78.

[13] 任伟健，黄丽杰，孙辉，等.不确定T-S模糊时滞系统的H_∞鲁棒控制[J].自动化与仪表，2015(11)：41-47.

[14] 余爱华.Logistic模型的研究[D].南京：南京林业大学，2003.

[15] 毕志伟，胡适耕.几类Lotka-Volterra模型的定性分析[J].应用数学，1990，5(4)：21-26.

[16] 于威威，王克.开放鱼场Gordon理论的进一步改进[J].经济数学，2003，20(1)：68-72.

[17] 徐道义.关于ROUTH-HURWITZ问题[J].数学杂志，1984，4(3)：273-277.

[18] LIU G P,HO D W C,YEUNG L F.Generalized Quadratic Stability for Perturbated Singular Systems[J].IEEE Conference on Dicision & Control,2003,3(3):2413-2418.

[19] 沃松林，吴建成.不确定非线性广义系统的鲁棒控制与保性能控制[J].系统工程与电子技术， 2007，29(6)：955-957，961.

Abstract: Guaranteed cost control problem of a class of nonlinear singular biological economic system was studied in this paper.Firstly,considering the influence of exotic species on the aboriginal fish population,starting with the artificial capture gains,purification capacity to the alien species and fish age factors,a nonlinear generalized model was developed,and then the equilibrium point was discussed.Besides,through the T-S fuzzy method,complex generalized model was transformed to linear one.Secondly,considering the disturbance affected by some natural factors was setting into satisfying Lipschitz conditions,using LMI method,the paper gave a set of conditions on the existence of guaranteed controller of a simplified nonlinear uncertain generalized model which satisfies guaranteed performance index.In the end,a set of numerical simulation was shown to verify the effectiveness of the study result.

Keywords: singular system; bio-economy system; uncertainty; guaranteed cost; T-S fuzzy system

GuaranteedCostAnalysisforaClassofNonlinearSingularBiologicalEconomicSystem

ZHANG Yi， ZHAO Hui-ying

(Shenyang University of Technology, Shenyang 110870, China)

10.3969/j.issn.2095-2198.2017.03.017

O23

A

2017-03-19

国家自然科学基金项目(61673099)；辽宁省自然科学基金项目(2015020007)

张翼(1971-)，女，辽宁辽阳人，副教授，博士，主要从事广义系统、生物数学等方面的研究.

2095-2198(2017)03-0278-10