结合差分曲率的空间模糊C均值图像分割算法

李国熊， 宋小鹏， 张 权， 桂志国,2

(1. 中北大学 电子测试技术国家重点实验室， 山西 太原 030051；2. 中北大学 仪器科学与动态测试教育部重点实验室， 山西 太原 030051)

结合差分曲率的空间模糊C均值图像分割算法

李国熊1， 宋小鹏1， 张 权1， 桂志国1,2

(1. 中北大学 电子测试技术国家重点实验室， 山西 太原 030051；2. 中北大学 仪器科学与动态测试教育部重点实验室， 山西 太原 030051)

针对基于空间信息的模糊C均值图像分割算法(sFCM)在对含噪图像分割时， 图像的噪声和边缘细节不能同时得到较为正确分割的问题， 本文提出了一种结合差分曲率的改进sFCM算法. 差分曲率(difference curvature)可以有效地区分图像边缘和平坦区. 将差分曲率引入到sFCM算法的空间函数中， 算法的函数相关性参数在每个像素点处自适应取值， 使改进算法在抗噪性能提高的同时， 对图像细节有着更好的分割效果. 实验结果表明： 在对含噪图像进行分割时， 本文提出的改进算法相比于sFCM及其衍生算法具有更好的模糊划分效果， 并有效地提升了sFCM算法的抗噪性和对边缘细节的保护能力.

模糊聚类； 图像分割； 图像去噪； 空间信息； 差分曲率

Abstract: For the problem of noise and details can not be segmented correctly at the same time when applying spatial information fuzzy c-means clustering algorithm (sFCM) to noise image segmentation, an improved algorithm of sFCM incorporating with difference curvature was proposed in this paper. Difference curvature can distinguish edges from ramp regions effectively. By applying difference curvature to the spatial function of sFCM, the function correlation parameters are determined adaptively in a single pixel so that the adapted method is more robust to noise, and results in better segmentation performance for details in the meantime. The experimental results indicate that the improved method achieve competitive results in fuzzy clustering, compared to sFCM and its variants. The noise tolerance and detail-preserving property are promoted effectively.

Keywords: Fuzzy c-means clustering; image segmentation; image noise; spatial information; difference curvature

图像分割就是把图像分成若干个特定的、 具有独特性质的区域的过程， 是图像处理领域的重要环节， 在航空航天、 生物医学工程、 工业检测、 机器人视觉、 地理测绘等领域有着广泛的应用， 是模式识别和计算机视觉中重要的研究课题. 图像分割的方法主要可分为： 阈值分割法， 基于边缘分割法， 基于形态学分割法， 神经网络分割法[1]， 免疫算法， 基于支持向量机分割法[2]和聚类方法等， 其中， 模糊C均值聚类算法(FCM)作为一种无监督算法已经在图像分割领域得到了广泛的应用.

标准FCM算法[3]通过模糊集合理论将数字图像进行有效的分割， 然而， 由于标准FCM算法在对图像分割时， 在目标函数最小化的原则下， 没有考虑像素点的空间邻域信息， 仅将图像的灰度信息作为分类依据， 导致图像中的噪声得不到正确的分类以及其边缘信息的丢失. 针对标准FCM算法对噪声敏感的问题， 有大量的学者进行了相关研究并从不同的角度提出了很多有效的改进算法[4-9]. 其中， Ahmed等人最早在目标函数中添加了空间邻域的约束项， 提出了FCM_S算法[4]， 其改进算法FCM_S1&S2提高了聚类计算速度； KFCM[5]算法用核函数替代了FCM中的欧式距离作为测度， 将像素灰度变换到新的特征空间进行处理； Cai引入了同时包含邻域空间距离以及邻域灰度差的相似测度， 提出FGFCM算法[6]； Zheng提出一种结合广义平均和多层聚类的GHFCM算法[7]， 该算法具有较好的拓展性; Zhao在s-FCM的基础上提出了一种结合非局部信息的自适应算法[9]. 上述算法均利用了图像的空间信息， 降低了图像分割结果中噪声点的比例. 然而， 这些算法需要一些参数(λ或α)在分割过程中使降噪和细节保持上达到平衡， 参数的取值大小决定了分割结果是偏向去噪还是保护边缘.λ或α由经验或者实验得到， 应用于图像所有像素点没有自适应的在具体像素处做出调整.

Chuang等人于2006年提出一种基于空间信息的改进FCM算法(sFCM)[10]， sFCM算法通过定义一种空间函数来重新计算像素隶属度， 从而达到对噪声点进行正确分割的目的. 在sFCM算法中， sFCM1,1和sFCM0,2分别为空间函数中两个函数相关性参数取不同的值对应的算法， 在这两种情况下， 图像的分割结果有很大差异. sFCM1,1算法降噪能力不足， 对噪声点分类不准确； sFCM0,2由于对隶属度过度平滑， 图像边缘细节得不到保护. 其改进算法有： 基于高斯空间信息的gsFCM[11]算法， 基于直觉模糊集的sIFCM[12]算法， 但上述算法同sFCM算法均存在明显的不足， 空间函数相关性参数为固定值， 不能随像素灰度以及其领域信息的变化而自适应调整， 去噪和保护边缘不能同时达到较好的效果. 因此， 为了让sFCM算法的函数相关性参数能在每个像素点自适应的取值， 本文引进差分曲率[13]， 来量化像素点为边缘的可能性， 使相关性参数的取值随该像素点的差分曲率变化而变化， 在对噪声正确分类的同时， 更好地保护图像边缘和细节.

1 标准FCM算法

FCM算法由Dunn提出， 而后由Bezdek对其进行了改进与推广[3]. 假设X=(x1,x2,…,xN)为待分类集合，X是由数字图像中N个像素组成的样本， 其中xj表示图像中第j个像素的灰度值. 将集合X分为c类， FCM算法通过对最小化目标函数迭代优化， 实现模糊聚类. 目标函数为

其约束项为

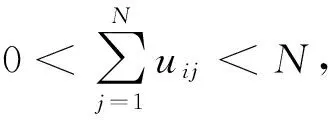
式中：Jm为各样本与其聚类原型的加权误差平方和；c为聚类数；N为像素个数；uij表示第j个像素属于第i类的隶属度函数；m为加权指数(一般取m=2)；vi为第i个聚类中心. 由拉格朗日数乘法， 得到使目标函数最小化的uij和vi

通过优化迭代， 直到满足条件

式中：ε为收敛阈值.

在目标函数最小化的原则下， 标准FCM算法在对图像分割时， 将图像的灰度信息作为分类的唯一依据， 所有特征向量之间互相独立， 邻域信息没有被利用， 忽略了图像中像素与像素之间的关系， 导致了算法对噪声的敏感度高， 图像中的噪声点容易被错误分类.

2 基于空间信息的FCM图像分割

针对FCM算法对噪声敏感的问题， Chuang 等人提出了sFCM[10]算法， 该算法定义了一种空间函数

式中：NB(xj)表示空间区域中以xj为中心的邻域. 空间函数是邻域像素隶属度函数的总和， 表示邻域区域属于第i类的可能性大小. 结合空间函数的隶属度函数定义为

式中：p和q是两个隶属度相关性参数， 带有参数p和q的空间FCM表示成sFCMp,q.p，q一般取值1和1(sFCM1,1), 或0和2(sFCM0,2). sFCM算法利用了像素的邻域特性， 改变了隶属度函数， 划分了更多的同类区域， 其p值越低，q值越高， 对图像噪声有着越好的分类能力， 但同时会对非噪声区域进行过度平滑， 导致图像的边缘和细节区域得不到保护； 当p值较高，q值较低， 图像的边缘和细节有较好的保留， 但此时噪声点的分类效果较差. 因此， 本文提出一种改进算法， 使p和q在图像分割过程中自适应取值： 在图像的噪声点或平坦区域，p值较大； 在含有边缘细节区域，q值较大， 从而让分割结果更为准确.

3 改进的sFCM算法

差分曲率[13]可以较好地区分图像的噪声和细节区域， 并广泛应用于图像处理[14,15]. 设图像梯度和切线方向的方向向量分别为

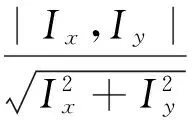
Iηη和Iξξ为图像I在梯度方向和水平方向的二阶导数

Iηη=

其中，

Iη=I·η=(IxIy)·=.

同理可得

差分曲率

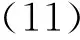
由式(11)可知， 在图像噪声点处， |Iηη|和|Iξξ|较大， 且几乎相等， 则该点处D较小； 在平坦区域， |Iqq| 和|Iξξ|都较小，D值较小； 而在边缘处， |Iqq|较大， |Iξξ|较小， 差分曲率D值则较大. 因此， 本文提出一种结合差分曲率的sFCM改进算法， 差分曲率用来量化像素点为边缘的可能性. 首先对差分曲率进行归一化

式中：Dmax为图像N个像素差分曲率的最大值. 然后对D′进行拉伸变换得到sFCM算法新隶属度函数中uij的指数

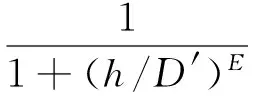
拉伸的目的在于让处于弱边缘细节处的像素点有较大的p值， 其模糊隶属度在分割迭代过程中不被过度平滑.h和E为拉伸参数，h越大， 拉伸曲线重心越大，E越大， 则拉伸斜率越大. 经实验验证，h=0.2，E=7的时候算法效果最佳， 令q′=2-p′. 最后得到新算法的隶属度

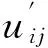
具体算法步骤如下： ① 初始化聚类数目c， 模糊指数m， 邻域半径r， 收敛参数ε； ② 给定初始聚类中心V0； ③ 根据式(11)～式(13)计算图像所有像素的差分曲率； ④ 根据式(2)， 式(5)和式(14)更新隶属度矩阵U； ⑤ 根据式(3)更新聚类中心V； ⑥ 重复4)和5)， 若满足条件： ‖V(l+1)-Vl‖<ε， 则停止迭代.

4 实验结果分析

为了比较改进算法与FCM， sFCM及其另外两种衍生算法sIFCM和gsFCM对图像的分割效果， 本文对叠加了噪声的Cameraman和House图像进行分割， 并采用划分系数(Vpc)[16]和划分熵(Vpe)来评价分割效果. 划分系数和划分熵被广泛运用于评价聚类效果，Vpc和Vpe定义为

式中： 划分系数Vpc越大， 划分熵Vpe越小， 则模糊聚类分割效果越好.

对自然图像Cameraman和House添加均值为0， 方差0.005的高斯噪声， 然后对图像进行分割， 分割类数为c=2， 邻域半径r=1， 收敛参数ε=0.02. sFCM， sIFCM和gsFCM算法中的p，q分别取1， 1与0， 2.

图 1 和图 2 分别为不同算法对Cameraman和House的分割结果. 从图中可以看出： FCM分割结果中， 大部分噪声点被错误分类； 当p，q取值1， 1时， 虽然sFCM， sIFCM和gsFCM的抗噪能力相对于FCM有一定的提高， 但仍存在较多噪声点， 而本文算法的分割结果中几乎没有孤立的噪声点， 图 1 中草地区域和图 2 中的墙面区域很好地显示了本文算法的抗噪性； 当p，q取值0， 2时， 从图 1 中相机支架部分和图 2 中的屋顶边缘可以看出， 相比于sFCM， sIFCM和gsFCM， 本文算法保留了最为完整的边缘细节.

表 1 为各种算法对噪声图像分割得到的划分系数和划分熵. 显然， 标准FCM算法的Vpc在所有算法中最小，Vpe最大； sFCM、 sIFCM和gsFCM算法中， 当p，q为1， 1时Vpc(Vpe)的值比p，q为2时大(小)； 而在所有算法中， 本文算法其Vpc最大且Vpe最小， 因此， 本文提出算法有着更好的模糊划分效果.

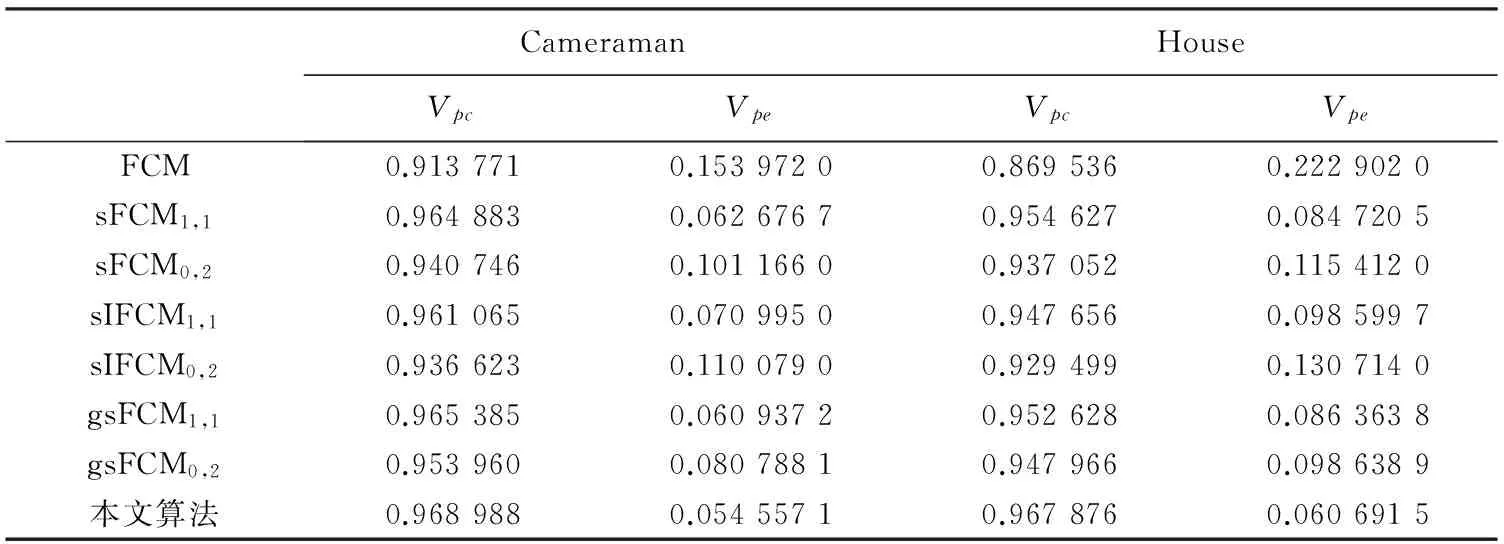
表 1 不同算法对噪声图像分割的Vpc和Vpe

图 1 Cameraman分割结果Fig.1 Segmentation result of Cameraman

图 2 House分割结果Fig.2 Segmentation result of House

5 结 论

本文在基于空间信息的FCM算法基础上， 引入了能较好地区分边缘区与非边缘区的差分曲率， 提出了一种改进的sFCM算法， 解决了在sFCM算法中， 由于p和q的取值不变性， 噪声和细节不能同时得到正确分类的问题. 新算法让p和q的值在分割之前自适应获取， 显示了较好的抗噪性能和对边缘细节的保护能力， 从而得到更好的聚类分割效果.

[1] Masoumi H, Behrad A, Pourmina M A, et al. Automatic liver segmentation in MRI images using an iterative watershed algorithm and artificial neural network[J]. Biomedical Signal Processing & Control, 2012, 7(5)： 429-437.

[2] Mizushima A, Lu R. An image segmentation method for apple sorting and grading using support vector machine and Otsu’s method[J]. Computers & Electronics in Agriculture, 2013, 94(94)： 29-37.

[3] Bezdek J C. Pattern recognition with fuzzy objective function algorithms[M]. New York, Plenum Press, 1981.

[4] Ahmed M N, Yamany S M, Mohamed N, et al. A modified fuzzy c-means algorithm for bias field estimation and segmentation of MRI data[J]. IEEE Transactions on Medical Imaging, 2002, 21(3)： 193-199.

[5] Zhang D Q, Chen S C. A novel kernelized fuzzy C-means algorithm with application in medical image segmentation[J]. Artificial Intelligence in Medicine, 2004, 32(1)： 37-50.

[6] Cai W, Chen S, Zhang D. Fast and robust fuzzy c -means clustering algorithms incorporating local information for image segmentation[J]. Pattern Recognition, 2007, 40(3)： 825-838.

[7] Zheng Y, Byeungwoo J, Xu D, et al. Image segmentation by generalized hierarchical fuzzy C-means algorithm[J]. Journal of Intelligent & Fuzzy Systems, 2015, 28(2)： 4024-4028.

[8] Krinidis S, Chatzis V. A Robust Fuzzy Local Information C-Means Clustering Algorithm[J]. IEEE Transactions on Image Processing, 2010, 19(5)： 1328-1337.

[9] Zhao F, Fan J, Liu H. Optimal-selection-based suppressed fuzzy c-means clustering algorithm with self-tuning non local spatial information for image segmentation[J]. Expert Systems with Applications, 2014, 41(9)： 4083-4093.

[10] Chuang K S, Tzeng H L, Chen S, et al. Fuzzy c-means clustering with spatial information for image segmentation[J]. Computerized Medical Imaging & Graphics, 2006, 30(1)： 9-15.

[11] Biniaz A, Abbassi A, Shamsi M, et al. Fuzzy c-means clustering based on Gaussian spatial information for brain MR image segmentation[C]. In Proceedings of the 19th Iranian Conference on Biomedical Engineering (ICBME ’12). Iranian Conference of Biomedical Engineering, Tehran, Iran, December 2012. Dehran： 2013： 154-158.

[12] Tripathy B K, Basu A, Govel S. Image segmentation using spatial intuitionistic fuzzy C means clustering[C]. Park College of Engineering and Technology. 2014 IEEE ICCIC, 2014 IEEE International Conference on Computational Intelligence and Computing Research, TamilNadu, India, Dec 2014. TamilNadu： 2014： 878-882.

[13] Chen Q, Montesinos P, Sun Q S, et al. Adaptive total variation denoising based on difference curvature[J]. Elsevier Image & Vision Computing, 2010, 28(3)： 298-306.

[14] 董婵婵, 张权, 郝慧艳,等. 基于差分曲率的偏微分方程图像降噪算法[J]. 计算机工程与设计, 2015(7)： 1850-1854. Dong chanchan, Zhang Quan, Hao huiyan, et al. Image denoising of PDE based on difference curvature[J]. Computer Engineering and Design, 2015(7)： 1850-1854. (in Chinese)

[15] Wang M, Zheng X, Pan J, et al. Unidirectional total variation destriping using difference curvature in MODIS emissive bands[J]. Infrared Physics & Technology, 2016, 75： 1-11.

[16] James C. Bezdek J C. Cluster Validity with Fuzzy Sets[J]. Journal of Cybernetics, 1973, 3(3)： 58-73.

SpatialFuzzyC-MeansClusteringIncorporatingwithDifferenceCurvatureforImageSegmentation

LI Guoxiong1, SONG Xiaopeng1, ZHANG Quan1, GUI Zhiguo1,2

(1. State Key Laboratory of Electronic Measurement Technology (North University of China), Taiyuan 030051, China； 2. Instrument Science & Dynamic Measurement, Ministry of Education Key laboratory of (North University of China), Taiyuan 030051, China)

1671-7449(2017)05-0392-06

TP391.41

A

10.3969/j.issn.1671-7449.2017.05.004

2017-03-02

国家自然科学基金资助项目(61671413)； 山西省自然科学基金资助项目(2015011046)

李国熊(1993-)， 男， 硕士生， 主要从事图像分割的研究.