基于组合模型的商业银行信用风险研究

2017-10-16邹柏松

三峡大学学报（人文社会科学版） 2017年5期

关键词：稳健性信用风险准确率

邹柏松

(中南民族大学经济学院，湖北武汉 443000)

基于组合模型的商业银行信用风险研究

邹柏松

(中南民族大学经济学院，湖北武汉 443000)

伴随着全球性的金融风暴和西方著名投行等金融机构的倒闭或被国有化，信用风险重新进入了众多风险分析家的视野。为了建立适用于我国国情的新的信用风险度量模型，使得我国的信用风险管理水平得以提高，开展信用风险量化管理技术的研究，在我国商业银行风险管理的实践中应用信用风险量化管理技术具有重要的现实以及理论意义。针对上述现状，本文分别建立装袋模型、基于预测值和基于预测结果(0/1)的组合模型，并将实证结果与单一模型结果进行了比较分析。通过比较发现，组合模型的预测准确率不一定高于每个单一模型，但准确率值却趋于准确率最高模型的值，同时组合模型的稳健性明显优于单一模型，总体而言，组合模型在一定程度上提高了模型预测精度，同时优化了模型稳健性，这使得模型更具有实际应用价值。

信用风险；统计方法；数据挖掘；组合模型

信用风险的复杂性随着金融市场的持续发展也越发明显，因此关于有效度量的风险也逐步增加。由于在我国严重违约数据及相关信贷统计资料不实，得出的信用风险度量的结论都不甚精确[1]。一般情况下，现代商业银行对客户初始违约概率的测算都是在量化分析其财务指标之后进行的，在这一基础上以其结果为根据对初始信用等级进行划分，然后通过不同信用等级的划分结果将客户分为某一类债务人，比如不违约类或者违约类，但国内应用量化模型进行风险评估的技术并不成熟，现有的量化方法大多只是利用一种统计方法或者数据挖掘方法进行建模及评估，不同的方法在稳健性及准确性方面有较大差异，导致了预测结果对方法有很大的依赖性，模型预测的准确性很有可能只是由某一方法自身的特点决定，使得模型预测结果有效性降低，因此，结合多种定性定量方法进行研究，使得各方法相互取长补短，建立组合分类预测模型以达到更高的预测精度是信用风险评估技术发展的必然趋势[2-3]。

基于此，对商业银行信用风险管理方面的实践来说，本文的研究具有重要的现实以及理论意义。首先，现实方面，可以为商业银行风险管理人员的研究提供思路，并通过实证合理评估信用风险，从而指导银行信用风险管理的实践；其次，理论方面，由于我国商业银行信用风险管理理念和文化缺失较为严重，机制不够健全，研究信用风险评估方法，有助于完善商业银行风险管理模式和制度，同时为风险管理研究提供理论支持。

一、数据预处理及模型评价概述

1.样本获取及数据预处理

第一，财务指标及数据获取。国际上通常以衡量企业财务状况的问题来替代衡量商业银行测度企业信用风险的问题，因为最主要的商业银行信用风险形成的原因即为企业不能如期还本付息[4-5]。通常情况下，需要通过各类财务分析指标对企业的财务状况好坏、盈利水平高低以及偿债能力大小等一系列数据来对企业的财务状况进行衡量。本文基于在财务评价中通常会使用到的财务指标体系，从投资收益、盈利能力、经营能力、偿债能力、资本构成、现金流量等方面入手选取了衡量上市公司财务状况的15个财务指标。

考虑到我国信用体系尚未建立完善，很难获知公司相关的违约信息，因此本文界定我国上市公司所包括的ST类公司为存在一定违约风险的企业。我国对存在异常状况的上市公司的股票交易是从1998年开始实行特别处理制度(ST，Special Treatment)的，而且因为财务异常问题被实行特别处理的上市公司具有很高的可度量性，因而比较容易确定样本。

论文采取截面数据分析法，从上市公司最新披露的2011年度财务数据中抽取样本，共获得360组原始数据，主要集中于批发与零售、房地产业、制造业等三个拥有比较密集上市公司的行业，包含88家有违约风险的公司(简称为ST类公司，标记为“1”)和272家无违约风险公司(简称为非ST类公司，标记为“0”)，原始数据来源于巨潮资讯网(www.cninfo.com.cn)以及和讯网(www.hexun.com)[6]。

第二，数据清洗及预处理。数据清洗的含义为发现并纠正相关数据文件中能够被识别的错误程序中的最后一道，主要包含了检查数据一致性，处理缺失值以及无效值等。在本文中，除了去除缺失值外，还需要剔除一些异常的值，常用的异常值剔除方法有以下三种：

(1)两倍、三倍标准差检验法。

基于小概率事件原理的方法即为两倍、三倍标准差检验法，在标准差σ已知的情况下，可考虑用该方法对某一组测定值中所存在的异常值进行检验[7-8]。根据正态分布的特点，偏差大于三倍标准差(3σ)以及两倍标准差(2σ)的测定值所出现的概率小于0.3%和5%，因此，结果为一个小概率事件，在离群点的偏差大于三倍或者两倍标准差的情况下，则能够剔除该值。

在样本容量大于30但是不知道σ值的情况下，判定可直接通过对相关样本值标准差s的计算代替σ来进行[9]。在数据平滑性较好且样本容量较大的情况下，这种方法的效果较好；但该方法在数据离散度大且样本个数少的情况下作用不明显。

关于两倍、三倍标准差检验法的步骤如下所示：

第二步，计算σ=s；

(2)ASTM检测法。

ASTM检测法是美国材料试验协会提出的一个对异常值检验的方法，检验统计量表示为：

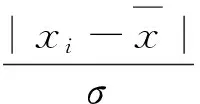
(3)t检验法。

常用于统计检验中的方法为t检验法，将除了待测定值xi外的测定值看作一个整体，并假设这个整体服从于正态分布是t检验法的基本思想。通过这些测定值对平均值x和s进行计算，并且将待测定值xi假设为样本容量是1的特征总体[10]。若xi和其余测定值属于同一个总体，则它和其余的测定值不应存在显著性差异，检验统计量为：

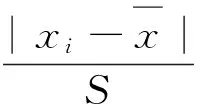
若根据xi计算得出的统计量T值大于在显著性水平α下计算出的t检验临界值，表明出现xi是一个小概率事件，考虑为异常值，将其舍弃，反之，则保留。

考虑到本文的数据样本容量比较大，且各类指标的相应取值范围也比较广，数据在一定范围内具有平滑性，所以选用两倍、三倍标准差检验法检测异常值，对标准选择5%的置信水平进行剔除。

通过剔除缺失值和异常值的样本，一共剔除了60个奇异样本，之后获得的样本数据集合为320个，其中ST类公司80个(标记为“1”)，非ST类公司240个(标记为“0”)。

因为每一个行业的业务范围和企业经营环境均有所差异，各项企业财务指标的衡量方法也有可能不同，因此本文将三个行业的财务指标数据分别除以各自对应行业的均值，此做法一方面消除了行业的影响，另一方面去除了量纲的影响，从而使数据的可比性更强。

第三，样本分组。为客观地检验模型的预测精度，获得的样本需要被分为测试样本和训练样本两部分，测试样本用来对模型的稳健性和精确度进行评估，训练样本用于模型的建立[11]。本文通过随机数抽样方法，训练的样本分别从非ST类公司以及ST类公司中随机抽取50%，剩余的部分作为测试样本来进行模型精确度的检验，根据2-折交叉验证法，以此抽取10次，构成10对样本。

2.模型评估方法概述

虽然有很多评价模型的方法，但是最主要的评价内容依然是模型的稳健性和精确性。因为无法用统计技术中较为常用的显著性、置信度、拟合优度等指标对基于数据挖掘方法的模型进行检验[12]，所以本文在采用以下方法对模型结果进行评估：

(1)模型的精确性检验

将测试样本带入训练后的模型中得出预测值，当预测值大于0.5时，判为违约公司(值记为“1”)，当预测值小于0.5时，则判为非违约公司(值记为“0”)，对结果进行统计得出相应的预测结果，实际和预测结果之中相符合的样本数与所有样本数的百分比称为准确率或者精确度，反之则被称为误判率，其中所体现的性能为精确性。本文所涉及到的准确率或者精确度分为三种，第I类准确率是第一种，第II类准确率是第二种，总体准确率是第三种，这几个指标在每个检验样本中的具体表达式如下：

第Ⅰ类准确率=所有违约公司中预测结果

正确的个数/违约公司个数

=P(预测值为1|实测值为1)

第Ⅱ类准确率=所有非违约公司中预测结果

正确的个数/非违约公司个数

=P(预测值为0|实测值为0)

总体准确率=总体预测结果

正确的个数/所有公司个数

(2)模型的稳健性检验

稳健性也可被理解为推广性，即在测试样本中应用经过训练模型时，其准确率的波动情况，若准确率波动较小且没有大幅度的下降，则说明对训练样本以外的样本来说，该模型适用性比较强，在实际运用时的可操作性也较强；反之，只能在特定样本中应用该模型，即使准确率较高，也不能进行推广应用，由此看来，模型的稳健性的重要性要强过模型的精确性[13]。模型稳健性检验方法主要有以下几种：

①平均绝对误差(MAE)

②平方差(SSE)

SSE=∑(ei)2

③均方差(MSE)

④根方差或标准差(RMSE)

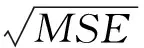
(3)模型收益(Gain)曲线检验

不断学习样本的过程即为模型的建立过程，学习所带来的收益(Gains)或者说学习的效果主要在模型“捕捉”到数据中所隐藏的规律和特征与否这一方面体现[14]。具体来说，即对于训练样本，模型能否通过学习有效总结概括出特定类别样本中存在的规律和特征，只有这样，模型在检验样本集上才可能有理想的分类预测能力。模型在这一方面的能力越强，其价值也就相应地越大，模型建立的意义也就越大，在实际应用中带来的“利润(Profit)”就越高。本文利用模型收益曲线图直观地评价分类预测的精度，其绘制方法如下：

首先，将真实值和预测概率值按预测概率大小从大到小排序；

其次，分别计算前10%，前20%，…，前100%的数据中预测结果为“1”的个数占真值“1”的总数的比例，记为n%；

最后，分别以点10%，…，100%为横坐标，n%为纵坐标绘制曲线图。曲线上升越快，则说明只需很少数据就可预测出来存在违约风险的大部分公司，则模型预测的效果就更好。

二、信用风险分类预测组合模型

1.基于装袋(Bagging)方法的分类预测模型

装袋(Bagging)是数据挖掘中一种提高分类准确率的方法。其思想可以通过举例来进行更为直观的说明：如果说你是一个病人，想要通过你的症状对病症进行诊断，你也许会看多个医生，而不是只选择某一个医生，在某一种诊断结果比其他的结果出现的次数多的情况下，你一般会将它作为最好的或者最终的判断，换句话说，最终判断是根据多数表决做出的，其中每个医生都具有相同的投票权重。现在，将医生换成分类器，就可以得到装袋的基本思想，直观地，更多医生的多数表决比少数医生的多数表决更可靠。

对训练样本进行建模，分别得到了Mi(i=1，2，3，4)这四个分类模型，为了分类一个未知样本X，在每个分类模型回到对其分类预测结果(0或者1)的情况下，记为一票。采用装袋分类器M*对结果进行统计，并将得到最高的类赋予X，当四种分类模型的分类结果出现两个1和两个0时，则采用0/1随机数方法决定。采用装袋方法得到的结果如下：

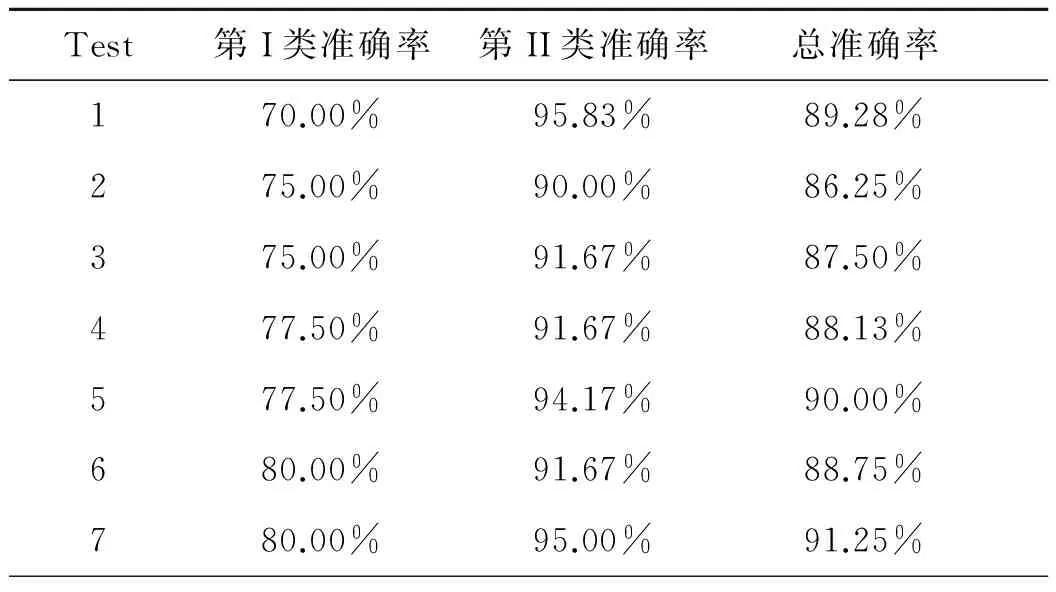
表1 装袋方法分类预测结果

(续上表)

该方法的总体准确率优于单一模型，第I类准确率及其稳健性也是最优的，因此装袋方法预测效果较好。

2.基于最小二乘法的加权组合分类预测模型

(1)权重系数求解

加权组合预测模型的关键在于确定权重系数。目前常用的求解组合预测模型权重系数的方法有很多，但基于最小二乘法的相关方法最为常用，即误差平方和最小的组合预测方法。

记f1t，f2t，f3t，f4t分别表示Logisitc回归模型、贝叶斯判别模型、BP神经网络模型和支持向量机模型在训练样本上的预测值，其中，t=1，…，160；训练样本实际的因变量值(0或1)用yt进行表示；四个模型的权重用w1，w2，w3，w4来表示，组合模型的预测值用ft进行表示。组合预测模型如下：

ft=w1f1t+w2f2t+w3f3t+w4f4t

S.T.w1+w2+w3+w4=1

记eit=yt-fitti，其含义为在第i种预测方法上样本t所存在的预测误差W=(w1w2w3w4)T，R=(1 1 1 1)T。模型的相关误差信息矩阵为：

相关的矩阵形式为：J=WTEW，因此，根据误差平方和最小化的原则，组合预测模型可转化为：

minJ=WTEW

S.T.RTW=1

将拉格朗日乘数引入来对上述最小值问题进行求解，构造的方程如下：

J=WTEW+λ(RTW-1)

极值存在的必要条件是J对W的一阶导数等于0，即

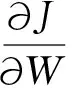
进而推得权重向量的表达式为：

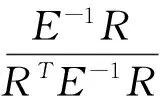
以上求解方法只是针对无非负限制的一般的权重，由此方法得出的权重系数可能会有负值出现的情况，关于权重系数是否可以为负的问题，理论界尚存在很多争议，因此，为确保权重系数具有可解释性，本文在求解和应用时将加以限制，即令wi∈[0，1]。

(2)加权组合分类预测模型实证结果

本文中，权重系数的求解通过Matlab软件计算可得。10次2-折交叉验证的权重系数结果如下：

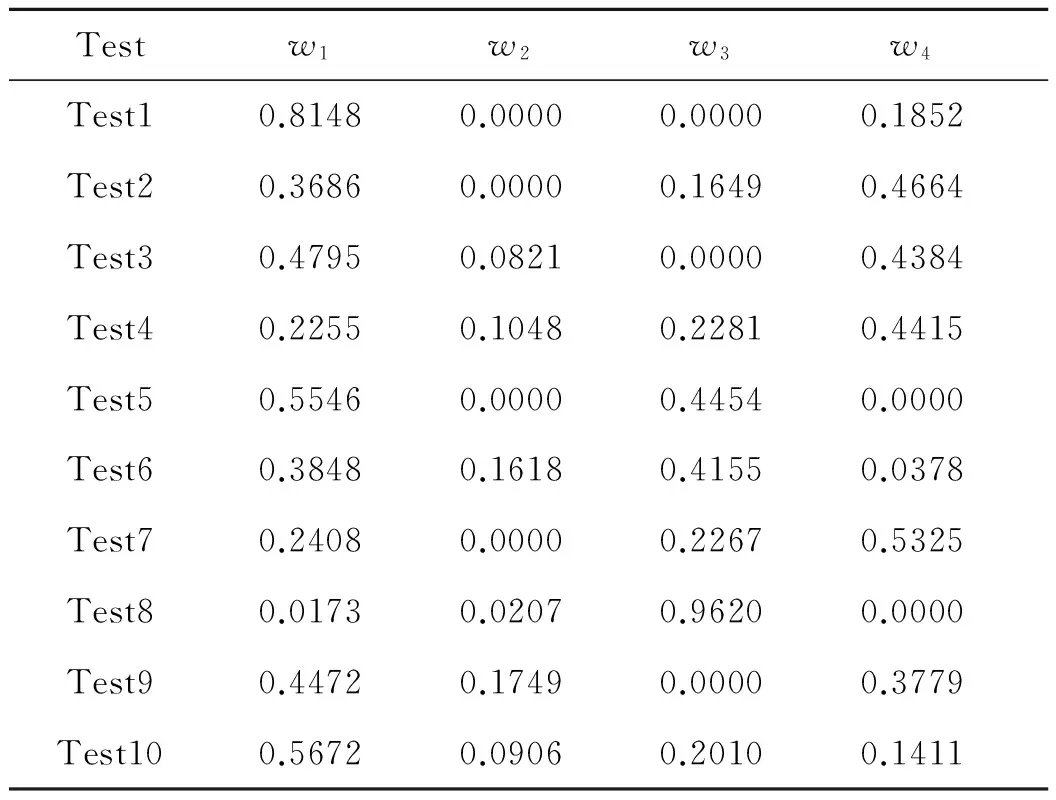
表2 权重系数求解结果

将上述结果与单一模型结果进行比较可得：

①分类准确率比较：加权组合分类预测模型10次结果的平均总准确率高于任一单一模型10次结果的平均总准确率，第I类准确率和第II类准确率的值居于四个单一模型准确率中间(这是由加权的特点决定的)，是接近准确率最高的一个，因此组合模型在一定程度上有效提升了模型的准确率。将组合模型和单一模型的模型收益图绘制在同一张图上也可以直观看出(如图1)，组合模型曲线上升最快，这更加验证了组合模型分类预测精度的提升。

图1 模型收益(Gain)汇总图

②模型稳健性比较：加权组合分类预测模型10次结果的稳健性指标值(包括：MAE、SSE、MSE、RMSE等)均小于权重不为零的相应单一模型的稳健性指标值(若某次测试中某一单一模型权重系数为零，则说明此次该模型对总体模型没有起到作用，无需考虑该模型的指标值)，且10次测试结果总准确率的标准差和MAE等稳健性指标的标准差均小于单一模型相应的值，该结果说明将组合模型应用于不同样本时，分类精度波动不大，优于单一模型，模型的稳健性得到有效提升，具有实际应用价值。

(3)基于预测结果(1/0值)的加权组合分类预测模型

基于预测结果(0或1)的加权组合模型准确率结果如表3。

表3 基于预测结果的加权组合模型准确率

基于预测结果加权的模型和基于预测值加权的模型分类准确率不相上下，但总体而言，基于预测结果加权的模型的稳健性略好。组合模型在一定程度上有效提升了单一模型的总体准确率，且其模型稳健性明显优于单一模型[15]。

三、结论

我国信用风险管理体系还不够完善，关于信用风险的度量方法多是借鉴国外现有模型，且以单一模型为主，使得评估方法不够稳定，单一模型自身的特点也会对结果造成很大影响。针对存在的问题，本文构建了加权组合分类预测模型，利用训练样本根据最小二乘方法确定权重，利用测试样本对单一模型和组合模型进行比较，最终完成整个信用风险评估体系的建设。模型预测的精确率得到一定程度上的提升，稳健性较之单一模型有了明显改善，由于良好的模型稳健性是模型具有实际应用价值的前提，因此本文构建的组合模型具有一定的实际意义。

[1] 白雪梅，臧微．信用风险对中国商业银行成本效率的影响[J]．财经问题研究，2013(2)：54-59．

[2] 顾海峰．信用平稳下商业银行信用风险测度模型及应用——基于模糊综合评判法[J]．财经理论与实践，2014(5)：8-12．

[3] 李天慈，李映照．商业银行中小企业贷款信用风险管理研究[J]．南方金融，2014(9)：93-95．

[4] 张洁，谭军．我国商业银行公司治理与信用风险管理绩效[J]．财会通讯，2013(6)：113-115．

[5] 周旭东，吕鹏展．商业银行信用风险管理的挑战[J]．中国金融，2013(12)：50-52．

[6] 陈云，石松，潘彦，等．基于SVM混合集成的信用风险评估模型[J]．计算机工程与应用，2016，52(4)：115-120．

[7] 郭莲丽，郭立宏，李建勋，等．基于证据理论的商业银行信用风险测度[J]．统计与决策，2013(19)：51-54．

[8] 杨北京，刘新海．基本征信数据挖掘分析[J]．现代管理科学，2015(8)：54-56．

[9] 万振海，刘铁英，张扬，等．信用风险评估中DKIPSO-SVC组合模型的仿真研究[J]．系统仿真学报，2015，27(8)．

[10] 吕劲松，王志成，隋学深，等．基于数据挖掘的商业银行对公信贷资产质量审计研究[J]．金融研究，2016(7)：150-159．

[11] 甘信军，张捷．商业银行信用风险控制的统计策略[J]．求索，2014(10)：47-51．

[12] 尹丽．基于KMV模型的中国商业银行信用风险评估[J]．统计与决策，2013(6)：157-159．