美国早期数学教科书中的极限概念

任芬芳，汪晓勤，陈玲玲



美国早期数学教科书中的极限概念

任芬芳1，2，汪晓勤3，陈玲玲4

（1．华东师范大学数学系，上海 200241；2．浙江师范大学行知学院，浙江金华 321004；3．华东师范大学教师教育学院，上海 200062；4．上海市朱家角中学，上海 201713）

围绕“极限概念”这一主题，考察了1870—1939年间出版的92种美国数学教科书，发现书中的极限定义分成动态、静态、动静结合3类；大多数为描述性定义，少部分为形式化定义．对照历史上数学家给出的极限定义得出结论：70年间，数学教科书中的极限概念的演变过程是极限概念历史发展过程的一个缩影．

早期数学教科书；极限的定义；极限的历史；认识论障碍

1 引 言

17世纪，牛顿（Isaac Newton，1643—1727）、莱布尼茨（G. W. Leibniz，1646—1716）创立了微积分，但牛顿发表的微积分论文由于不严密而受到质疑．直到19世纪柯西（A. L. Cauchy，1789—1857）创立极限理论，才为微积分打下坚实的基础，完善了微积分．没有极限，微积分岌岌可危．若对极限没有深刻的认识，也就不可能透彻地理解微积分的本质，因此，极限理论的学习是微积分学习的重要环节，而极限概念（尤其是它的分析定义）的教学则是微积分教学的难点之一．

著名数学家和数学史家克莱因（M. Kline，1908—1992）曾指出：“每一位中学和大学数学教师都应该知道数学史；有许多理由，但最重要的一条理由或许是：数学史是教学的指南．”[1]研究概念的历史、确定其发展缓慢和产生困难的时期有助于指明认识论障碍的存在[2]．对产生于18世纪的极限概念来说，19、20世纪的数学教科书能很好地体现其发生、发展的规律．为了更好地进行极限理论教学，围绕极限概念这个主题，以极限的描述性定义为主要研究对象，对美国20世纪中叶以前出版的数学教科书进行考察，试图回答以下问题：92种教科书有哪些极限定义？这些定义是如何演变的？有何特征？与历史上的极限概念有何联系？

2 研究对象

选取20世纪中叶之前出版的92种美国数学教科书进行研究．其中，代数教科书有25种（其中13种用于大学，其余用于中学．因查阅美国大学相关数学教科书，发现绝大多数没有出现极限定义，而是直接使用极限概念，故将这13种大学代数教材一起讨论），几何教科书有67种（均用于中学）．主要作者有：G. A. Wentworth（1835—1906）、D. E. Smith （1860—1944）、W. Wells（1851—1916）等．若以10年为一段，图1给出了各教科书的时间分布情况．

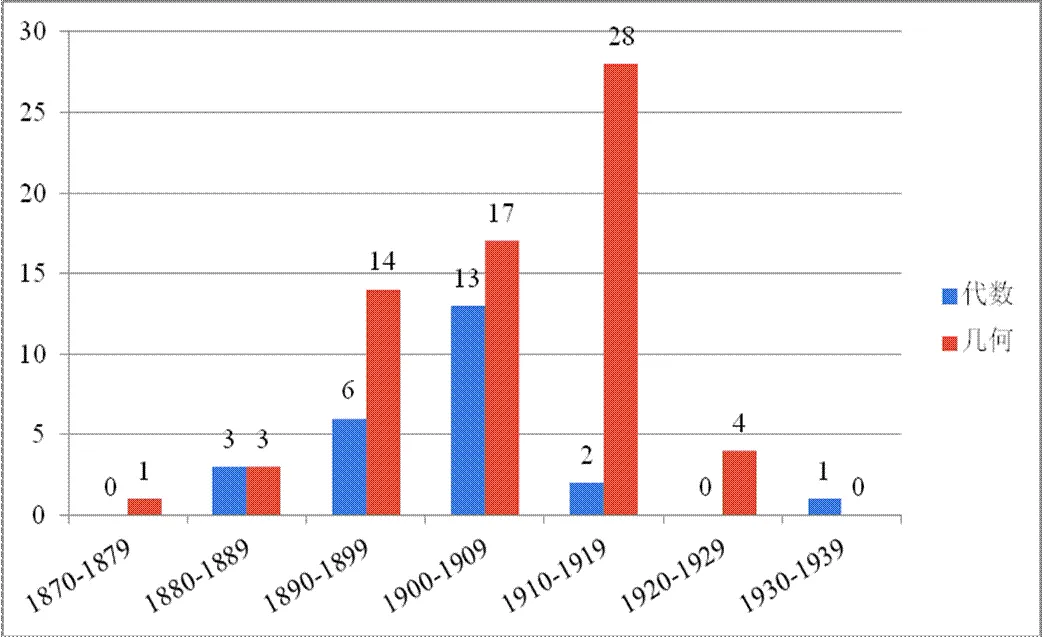
图1 92种教科书的时间分布

在92种教科书中，极限概念散见于各种不同知识点的章节中，并没有很明确的归属．

就25种代数教科书而言，所在章节大致可以分为“零与无穷”、“级数与极限”、“变量与极限”、“函数与极限”、“极限”及“线性方程”6类，详见表1．

表1 极限概念在25种代数教科书中的章节分布

可以发现，“变量与极限”这一章节所占比例最高，为44%；在有关章节的标题中出现“极限”的教科书共计20种，占80%，但极限内容单独成章的教科书仅有5种．

就67种几何教科书而言，所在章节大致可以分为“圆与圆的度量”、“比与比例”、“极限理论”、“量”、“多面体、圆柱、锥体”及“附录”6类，详见表2．

表2 极限概念在67种几何教科书中的章节分布

很明显，“圆与圆的度量”所占比例最高，为70%，远高于第二位的“比与比例”；而极限内容单独成章的教科书仅有4种，占6%．

92种教科书中章节标题涉及“极限”的并不多，共24种，仅占26.1%．

统观92种教科书中的极限概念，其呈现方式分为5种：直接给出定义，先给引例再给定义，先给定义再给例子，引例、定义、例子3者皆有，只有描述没有定义．

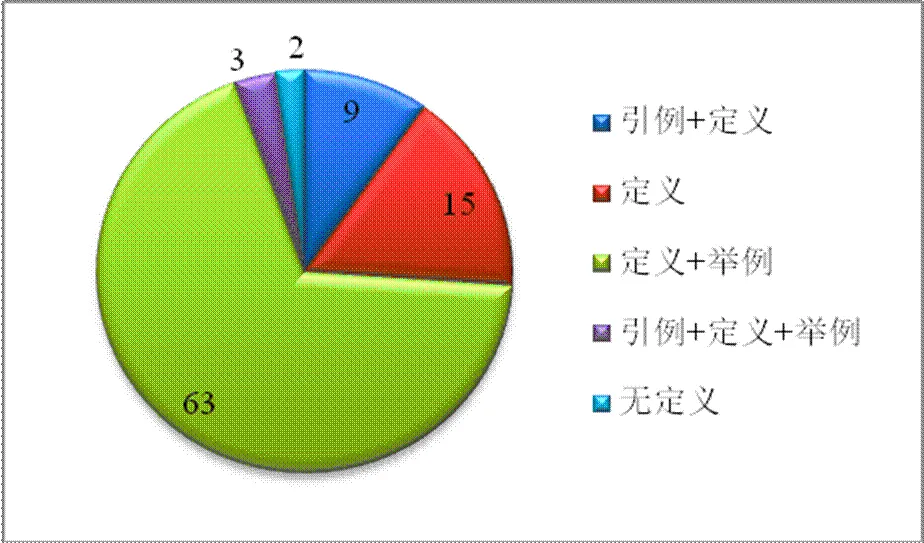
图2 极限概念在92种教科书中呈现方式分布

如图2所示，先给定义再给例子的方式所占比例最高，为68.5%；仅给出定义的教科书所占比例也不少，为16.3%．

3 极限定义的类型

3.1 分 类

统计发现，92种教科书给出的极限定义主要可分成3类：第一类是动态的描述，“变量越来越接近或趋近常量”，称为“动态定义”；第二类则是静态的描述，“变量与常量的差小于任意给定的数”，称为“静态定义”；第三类则把两者结合起来使用，在一个定义中既有“趋近”也有“差”，称为“动静结合定义”．此外，其中两种教科书并未给出明确的定义，只是用引导性的描述语言阐述“极限概念”．

表3列举了92种教科书中所出现的3类定义的典型形式，其中动态定义5个、静态定义4个、动静结合定义7个．

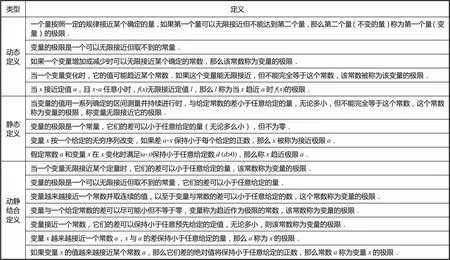
表3 92种教科书中出现的极限定义的典型形式

下面给出“没有明确定义”的“极限概念”：

（1）提问什么是变量、常量．

（2）给出例①：点在线段上移动，第一秒到达中点，第二秒到达剩下一半的中点，第三秒到达剩下四分之一的中点……随后提出3个问题：产生了哪两个不同的距离；距离接近哪个距离，何时达到；距离接近哪个距离，何时达到．例②：将分数改写成一位小数、两位小数、三位小数、……随后提问：每次改写对小数的值有什么影响，接近多少；每次改写对与小数的差有什么影响，接近多少．

（3）提问什么是变量的极限、上极限、下极限．

（4）变量可以与它的极限接近到什么程度．

（5）继续举例：①一个长方形的短边连续变化，问哪些边是变量，极限是多少；角是变量吗，极限是多少；面积受到什么影响，极限是多少？为什么逐渐减小的边不能变成零？②圆内接正多边形（如正方形或等边三角形），二等分每段弧，并连接成弦，得到两倍边数的内接正多边形，类似地得到四倍、八倍、……边数的圆内接正多边形，问变量的最终形式与极限．

（6）提及有时变量不能无限接近极限，如上述圆内接多边形的例子倒过来．

上述提问并没有给出答案，也没有给出具体定义，只是引导学生慢慢了解什么是“变量的极限”．但毫无疑问，这个过程蕴含了极限概念．

3.2 分 布

3类定义的总数基本持平，个别教科书出现两类定义，其中动态定义27个，静态定义33个，动静结合定义37个．图3是3类定义的具体时间分布，以10年为分布单位．

如图3所示，92种教科书的极限概念开始于动态定义，结束于静态定义．前后各20年的教科书数量较少，重点考察中间30年，即1890—1919．有一个很明显的现象：1890—1899这10年动态定义多于其它两种定义，1900—1909这10年3种定义差不多，而1910—1919这10年动态定义少于其它两种定义．

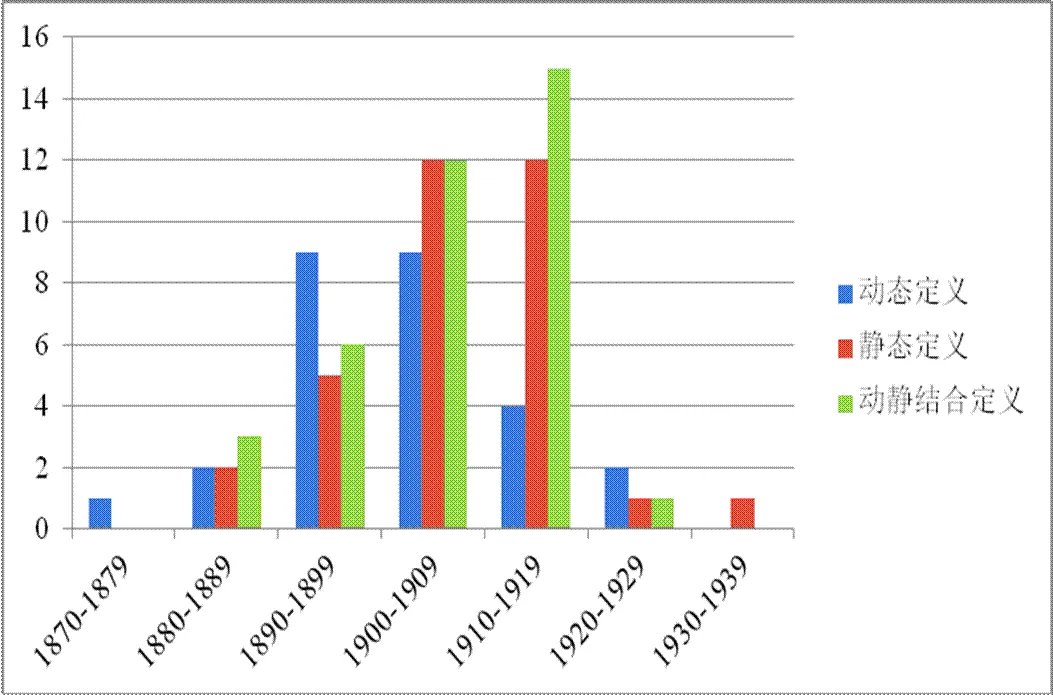
图3 3类定义的时间分布

3类定义中既有纯文字的“描述性定义”，也有字母、符号表示的“形式化定义”．图4呈现的是这些教科书中极限定义的演变过程，图5是这些定义的数量分布．

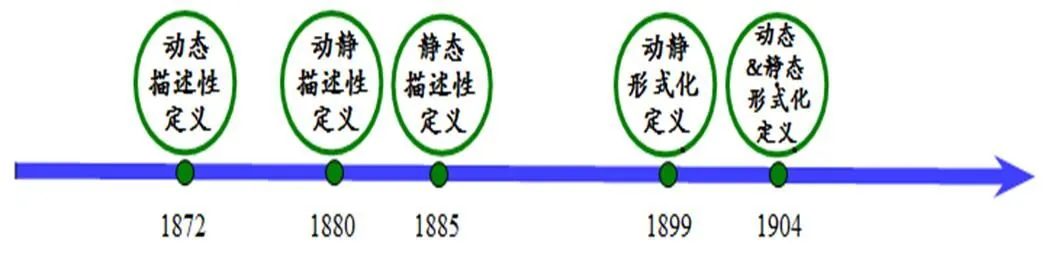
图4 极限定义的演变

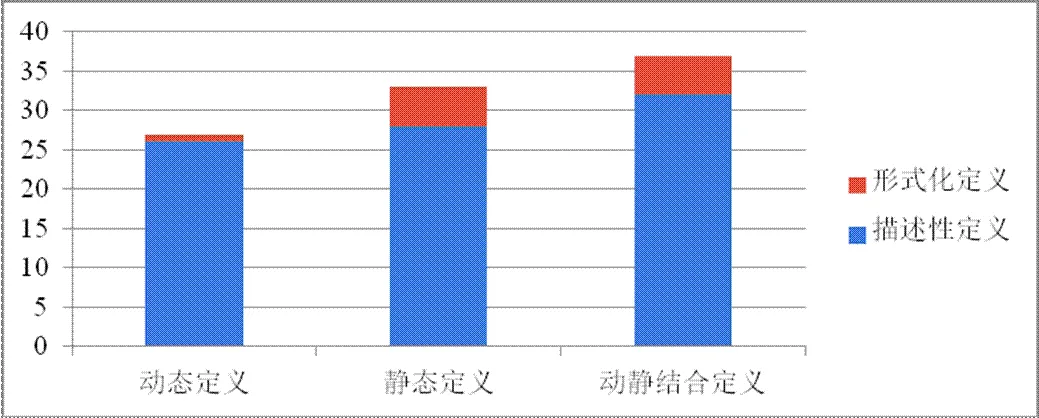
图5 极限定义的数量分布

第一个动态定义出现在1872年，出自塔班（E. T. Tappan, 1824—1888）的《平面与立体几何》[6]，是描述性定义．1904年出现形式化定义，即：当接近定值，且-任意小时，无限接近定值l，那么l称为当趋近时的极限．该定义出自查理·斯密（C. Smith，1844—1916）的《初等代数》[20]，是全部动态定义中唯一一个形式化定义．

第一个静态定义出现在1885年，即：当变量的值能用一系列确定的区间测量并持续进行时，与给定常数的差小于任意给定的量，无论多小，但不能完全等于这个常数，这个常数称为变量的极限，出自温特沃斯（G. A. Wentworth, 1835—1906）的《平面与立体几何基础》[9]，是描述性定义．1904年出现形式化定义，即：变量按一个给定的无穷序列改变，如果差保持小于每个给定的正数，那么被称为接近极限，出自范（H. B. Fine，1858—1928）的《范氏大代数》[19]．1909年出现了含有“差的绝对值”的形式化定义，即：假定常数和变量在变化时满足保持小于任意给定数(>0)，那么称趋近极限，出自里茨（H. L. Rietz，1875—1943）与克雷索恩（A. R. Crathorne，1873—1946）的《大代数》[22]．静态定义中共有5个形式化定义，其中两个使用“”，3个使用“”或等价形式．这些形式化定义均出现在代数教科书中，但没有必然规律．

而第一个动静结合定义出现在1880年，即：一个量按照一定的规律接近某个确定的量，如果第一个量可以无限接近但不能达到第二个量，那么第二个量（不变的量）称为第一个量（变量）的极限，出自布拉德伯里（W. F. Bradbury，1829—1914）的《初等几何》[7]，也是描述性定义，比第一个静态定义早5年．1899年出现形式化定义，即：变量越来越接近一个常数，与的差保持小于任意给定的量，那么称为的极限，出自比曼（W. W. Beman，1850—1922）的《新平面与立体几何》[15]．动静结合定义中共有5个形式化定义，其中两个出现在代数教科书中，3个出现在几何教科书中；且与前面两类不同，首次出现形式化定义是在几何教科书中．

综上，描述性定义贯穿整个考察年代，而形式化定义虽有出现，却寥寥无几．

3.3 释 例

由于极限概念难以理解，绝大多数教科书都给出了具体的例子对极限定义加以阐释，根据这些例子的特征将其分成4类．

3.3.1 “芝诺悖论”型

即：动点沿着线段从点往点运动，首先到达的中点，再到达的中点，然后到达的中点……在这个运动过程中，动点所经过的距离趋近于线段的长度，即线段长度就是距离的极限．

这类例子出现在绝大多数教科书中，与中国古代《庄子·天下篇》中的“一尺之棰，日取其半，万世不竭”有异曲同工之妙，不论哪一类定义都可以使用．上述形式常用于阐释动态定义或动静结合定义．

而教科书中出现的这类例子还有两种形式：

（2）将一个长方形二等分，其中之一再二等分，再取其一二等分，……依次类推，小长方形的面积依次是原长方形面积的,,,, …，可以小于任意所给定的常数．这种形式出现较少，用于阐释几何教科书中动态定义．

3.3.2 “无限小数”型

3.3.3 “圆的度量”型

首先指出圆内接（外切）正多边形（如正方形或等边三角形）将圆分成若干等弧，二等分每段弧，并连接弦，得到两倍边数的内接正多边形；重复这个过程，依次得到四倍、八倍……边数的内接（外切）正多边形．紧接着问产生了哪些变量，这些变量的极限是多少．如圆周长、圆面积、圆半径分别是圆内接（外切）多边形周长、面积、边心距的极限，等等．

这类例子主要用于阐释在与圆相关的章节中出现的极限定义，以动静结合定义为主；既有正多边形“接近”圆的过程，也有相应两个量的“差”可以小于任意给定的量．

3.3.4 “几何元素”型

主要有以下几种情况：

（1）长方形的短边连续变化，问边、角、面积的极限分别是多少？并提出一个很关键的问题：“为什么逐渐减小的边不能变成零？”

（2）增大等腰三角形的两腰长，则两底角不断增大，趋近直角，但是不能取到直角，这个过程中两底角的极限是直角．

（3）增大直角三角形的其中一条直角边，则其对应的角不断增大，趋近直角，但是不能取到直角，这个过程中该锐角的极限当然也是直角．

这类例子主要用于阐释动态定义，涉及几何图形（圆除外）的元素，出现在几何教科书中，强调“动”的过程．

综上，4类例子与定义类型有一定的相关性．如“一尺之棰”型可静可动，不同的形式对应不同的定义类型．

此外，这4类例子均符合定义中的“变量与常量不能相等”这一点，或许是人们认为“变量不能等于极限”的原因之一．

4 讨 论

4.1 数学家给出的极限定义

古希腊诡辩学派的安提丰（Antiphon，公元前426—公元前373）在解决“化圆为方”的问题时提出如下方法：作圆内接正方形，将边数加倍，得内接正八边形；再将边数加倍，得内接正十六边形……；依此类推，最后正多边形穷竭了圆．后来阿基米德将其发展为“穷竭法”，是极限思想的萌芽．当时的“极限”观念是纯几何的，而目前常用的极限概念是数量的[26]．

公元18世纪，随着微积分的创立，数学家们对极限概念开始进一步讨论．微积分的基础薄弱，究其原因是算术观念与几何观念的混杂，这也是牛顿与莱布尼兹工作中许多含糊不清的根源[26]．直到19世纪，柯西将极限概念明确为算术的[26]，并建立极限理论，才为微积分奠定了坚实的基础．

极限概念从最初的“几何”观念转变为后来的“数量”观念，这一事实与92种教科书中几何教科书居多相符．

在微积分创立前后的数个世纪，数学家们曾经给出的、较有代表性的极限定义有：

1655年，英国数学家沃里斯（J. Wallis，1616—1703）在《无穷小算术》中提出了函数极限的算术概念：它是被函数逼近的数，使得这个数和函数之间的差能够小于任一指定的数，并且当过程无限地继续下去，差最终将消失[27]．

1735年，英国数学家罗宾斯（B. Robins，1707—1751）在《论艾萨克·牛顿爵士的流数法以及最初比与最终比方法的本质与可靠性》一书中这样定义极限：当一个变量能以任意接近程度逼近一最终的量（虽然永不能绝对等于它），我们定义这个最终的量为极限[28]．

1821年，法国数学家柯西在《分析教程》中写道：当一个变量逐次所取的值无限趋近一个定值，最终使变量的值和该定值之差要多小就有多小，这个定值就叫做所有其它值的极限[29]．

约1860年，德国数学家魏尔斯特拉斯（K. W. T. Weierstrass，1815—1897）认为上述定义不够明确而给出了现在所使用的定义：如果给定任何一个正数，都存在一个正数，使得对于区间内的所有都有，则说在处有极限[29]．

可以发现，这4个的极限定义包括了动态、静态及动静结合定义；先有描述性定义，再有形式化定义；从有记载的极限定义演变为静态形式化定义跨越了两百多年，如图6所示．

图6 数学家的极限定义

罗宾斯给出的定义强调了变量与其极限不能相等，有38.7%的教科书的定义也体现了这一点；创立了极限理论的柯西所给出的极限定义是动态描述性定义；97个定义中只有11个形式化定义，但与维尔斯特拉斯的定义相比还是有所欠缺的．

教科书中极限定义的演变体现了极限概念的历史演变过程．

4.2 极限概念的认识论障碍

极限概念在历史上有4大认识论障碍[2]：（1）数形未能结合；（2）无穷大和无穷小的概念；（3）极限概念的定义形式；（4）极限能否取到？下面结合教科书中的极限概念对这4大认识论障碍进行分析．

（1）早期教科书所用的阐释定义的例子基本上是“路归路，桥归桥”，几何教科书用几何例子，代数教科书用代数例子．即使代数教科书的定义用几何例子来阐释，也没有将其转换成代数形式，基本没有实现“数形结合”．

究其缘由，或是因为把相应的几何例子代数化并不容易，且用描述性语言来说明定义更容易让学习者接受．

（2）动态定义一般用“越来越接近”或“趋近”这类词来表示变化过程，只有两个定义例外，一个用“足够的步数”、而另一个定义用“无穷多个连续的值”．而静态定义一般用“无论多小”或“小于任意给定的量”来表示变量与其极限的差．说明早期教科书避免出现“无穷大”和“无穷小”的概念．

（3）从极限定义形式的演变来看，总共3类97个定义中，描述性定义占有绝对优势，且贯穿始终．形式化定义首次出现在1899年，在考察的这些定义中出现较早，但其后处于弱势，随机出现，总共只有11个．67种几何教科书总共只有3个形式化定义，而代数教科书1903年才出现形式化定义，但稍晚的代数教科书基本上都采用了形式化定义．

（4）92种教科书中最早出现的极限定义强调“变量不能达到常量”，即变量不能等于极限，共有36种教科书提及，占38.7%．这点随着时间的推移慢慢弱化、定义中不再要求，但阐释定义仍然是“不能相等”的例子，容易产生误解．

因此，92种教科书中呈现的极限定义特征及其释例体现了历史上人们对极限概念的4大认识论障碍．

5 结论与启示

综上所述，早期教科书中的极限定义可以分成动态定义、静态定义、动静结合定义3类．这3类定义在数量上相差不大．这些定义大多数为描述性定义，且贯穿始终；少部分为形式化定义，零星点缀．整体来看，92种教科书中呈现的极限定义及其特征体现了人们对极限概念的不同理解．

基于以上分析得到如下启示．

（1）对教科书编写的启示．

（2）对教学要求的启示．

从极限思想的萌芽到极限理论的建立经历了数千年，那么多伟大的数学家对极限尚不能很快融会贯通，对学生当然也不能操之过急．92种教科书中出现的极限定义不完善的地方，如“变量与极限的差小于任意给定的常数”、“变量不能等于它的极限”、没有涉及“某一变化过程”等，其实也是学生学习极限概念时容易出现的错误．了解了这些教科书中的极限定义以后，也就知道学生出现的这些错误是很正常的．在了解学生认知发展规律的前提下，在教学中对这些地方需要特别关注．

（3）对教学设计的启示．

教科书的定义呈现方式中有示例（包括引例和举例）的占84%，而极限定义的理解又是一个难点，所以不论教科书中采用何种形式，在教学设计时可以采用“引例+定义+举例”的形式．引例可以帮助学生对极限有一个初步的了解，形成概念雏形；随后给出极限定义，帮助学生对极限有一个统筹的观点，并与自己形成的概念雏形加以比较；而后举例说明，帮助学生理解极限定义、并修正自己的概念雏形，最终将极限定义内化．

英国数学家德摩根（A. De Morgan，1806—1871）强调数学教学中的历史次序，认为教师在教代数时，不应该一下子把新符号都解释给学生，而应该让学生按历史顺序去学习符号[3]．虽然早期教科书中的极限概念还不是很完善，但正是这种不完善，才更符合人们的认知过程，据此可以确定学生对极限概念理解的认识论障碍．从极限思想的初步萌芽，到柯西初步创立极限理论，再到数学教科书的出版，历经数千年的时间，仍然没有、的影子，那么要让学生们短短数十分钟掌握“”语言并不是一件容易的事情．美国早期数学教科书是一面镜子，从中折射出人们理解极限概念的困难，据此完全可以预测、并深刻理解今日课堂上学生的学习困难．

[1] 汪晓勤，欧阳跃．HPM的历史渊源[J]．数学教育学报，2003，12（8）：24-27．

[2] David Tall.[M]. Dordrecht, Boston, London: Kluwer Academic Publishers, 1991.

[3] 蒲淑萍，汪晓勤．学生对字母的理解：历史相似性研究[J]．数学教育学报，2012，21（6）：38-42．

[4] 汪晓勤．19世纪末20世纪初美国几何教科书中的勾股定理[J]．中学数学月刊，2014，（6）：48-52．

[5] 李玲，汪晓勤．美国早期代数教科书中的数列知识[J]．中学数学月刊，2014，（7）：53-56．

[6] Tappan E. T.[M]. Cincinnati: Wilson, Hinkle & Co., 1872.

[7] Bradbury W F.[M]. Boston: Thompson, Brown, &.Co., 1880.

[8] Wells W.[M]. Boston: Published by Robert S. Davis & Co., 1882.

[9] Wentworth G A.[M]. Boston: Ginn, Heath, & Co., 1885.

[10]  Newcomb S.[M]. New York: Henry Holt & Company, 1887.

[11]  Wells W.[M]. Boston: Leach, Shewell, & Sanborn, 1889.

[12]  Macnie J.[M]. New York: American Book Company, 1895.

[13]  Gillet J A.[M]. New York: H. Holt & Company, 1896.

[14]  Dodd A A, Chace B T.[M]. Kansas: Press of Hudson-Kimberiyy Publishing Co., 1898.

[15]  Reman W W.[M]. Boston, U.S.A.: Ginn & Company, Publishers, 1899.

[16]  Boyd J H.[M]. Chicago: Scott, Foresman & Company, 1901.

[17]  Milne W J.[M]. New York: American Book Company, 1902.

[18]  Colaw J M, Ellwood J K.[M]. Richmond: B. F. Johnson Publishing Co., 1903.

[19]  Fine H B.[M]. Boston: Ginn & Company, 1904.

[20]  Smith C.[M]. New York: The Macmillan Company; London: Macmillan & Co., 1904.

[21]  Schmall C I, Shack S M.[M]. New York: D. Van Nostrand Company, 1904.

[22]  Rietz H L, Crathorne A R.[M]. New York: Henry Holt & Company, 1909.

[23]  Hart C A, Feldman D D.[M]. New York: American Book Company, 1912.

[24]  Wilczynski E J, Slaught H E.[M]. Boston: Allyn & Bacon, 1916.

[25]  Wilson N R.[M]. New York: Oxford University Press, 1920.

[26] 波耶 C·B．微积分概念史[M]．上海师范大学数学系翻译组译．上海：上海人民出版社，1977．

[27]  M·克莱因．古今数学思想（第一册）[M]．张理京等译．上海：上海科学技术出版社，2014．

[28]  M·克莱因．古今数学思想（第二册）[M]．万伟勋，石生明，孙树本等译．上海：上海科学技术出版社，2014．

[29]  M·克莱因．古今数学思想（第三册）[M]．邓东皋，张恭庆等译．上海：上海科学技术出版社，2014．

[30]  Alexanderson G L, Kline M. An Interview with Morris Kline: Part 1 [J]., 1979, 10(3): 172-178.

Limit Concept in the Early American Mathematical Textbooks

REN Fen-fang1, 2, WANG Xiao-qin3, CHEN Ling-ling4

(1. Department of Mathematics, East China Normal University, Shanghai 200241, China;2. Xingzhi College Zhejiang Normal University, Zhejiang Jinhua 321004, China;3. Teacher Education College, East China Normal University, Shanghai 200241, China;4. Shanghai Zhujiajiao Secondary School, Shanghai 201713, China)

In this paper, the definitions of limit in 92 American mathematical textbooks published before the middle of the 20th century are examined. It was found that there are three types of definitions of limit: dynamic, static and mixed and the majority of them are descriptive definitions. Compared with the definitions given by mathematicians, the evolution of the concept of limit was just a miniature of its long history.

early mathematics textbooks; definition of limit; history of the concept of limit; epistemological obstacles

[责任编校：周学智]

G40-059.3

A

1004–9894（2017）04–0038–06

2017–03–20

上海市教育科学研究项目——中小学数学课程的有效设计，子课题——中小学数学教科书中数学文化素材的案例设计（D1508）；浙江省2014年高等学校访问学者专业发展项目——HPM视角下的微积分教学研究（FX2014008）

任芬芳（1982—），女，浙江东阳人，华东师范大学博士研究生，主要从事数学史与数学教育研究．