高职数学课程范式：从模块化到类别化

游安军，曹广福，杨 裕



高职数学课程范式：从模块化到类别化

游安军1，曹广福2，杨 裕1

（1．珠海城市职业技术学院，广东珠海 519090；2．广州大学数学与信息科学学院，广东广州 510006）

近20年来，人们对高职数学课程性质的认识发生了明显变化：从侧重“基础性”转向了强调“工具性”，即高职数学要“突出应用性，与专业结合，为专业服务”．这既是职业院校各个专业向数学课程提出的诉求，也是高职数学课程的特点．为了反映这种诉求，中国高职数学课程经历了由“压缩型”向“模块化”过渡，但囿于“必需、够用”原则和“压缩型”思维方式的影响，“模块化”并未实现这个目标．只有跳出传统的高等数学框架，进行跨学科思考，实施“类别化”数学课程建设，才能实现高职数学工具性的课程愿景．

高职数学；课程范式；压缩型；模块化；类别化

1 引 言

近20年来，中国高职数学课程经历了由本科“压缩型”向“模块化”转变．在此过程之初，许多院校都没有清晰地认识高职教育在培养目标、教学内容方面的特点，把高职教育办成了普通专科教育，此时《高等数学》基本上是本科“压缩型”，主要特点是：知识体系封闭，忽视专业应用[1~2]，保持着一种以不变应万变的姿态．

2006年以后，中国高职教育规模迅速扩大，高职生的基础素质和学习能力普遍下降．同时，随着人们对职业教育认识不断深入，各个专业科目的课程与教学改革也渐次展开，比如，工学结合的推进和技能实训的加强，使得数学课程的学时不断减少，由最初144学时降为108学时，直至现在60学时左右．应该说，这种变化是普遍的、必然的．于是，人们开始重新思考高职数学课程的性质和定位，逐步从侧重“基础性”转向强调“工具性”，并提出了高职数学要“突出应用性，与专业结合，为专业服务”思想[3]．

这种思想不是某个地区、某个人的主观臆断，而是高职院校相关专业对数学课程的普遍要求．从根本上说，它是由高职教育的目标和特点，以及高职生的基础素质、学习能力、数学水平等决定的．著名职教专家戴士弘教授认为：“职业院校的学生不是来泛泛地接受知识、积累知识的，而是来学习实用就业能力的，他要能在未来职业岗位上解决实际问题．”[4]也就是说，高职数学不能单纯停留在培养思维能力和打基础的层面（这是基础教育的主要任务），而必须根据各自的专业目标和要求，加强数学的应用性教学．数学菲尔兹奖得主、美国数学家D. B. Mumford认为，数学教育应当进行十分严肃的努力，从思想上重视应用．他在“改革微积分——为了数百万人”一文中说：“我们讲授微积分，是为了希望我们的学生中的一小部分能追随我们对严谨的热爱，还是为了使我们大多数学生将来在他们的专业中有应用微积分的能力？”[5]显然，成千上万学生需要的是应用性数学，这样的数学能够给他们的职业素养和专业能力的可持续发展提供支持．进一步地，如果不能在课程层面就处理好数学知识与专业应用之间的关系，就不能构建出具有鲜明专业特色的、工具性课程，课堂教学的诸多问题（如数学学习兴趣、应用能力培养等）也不可能从根本上得到有效解决．

在高职数学课程的生存空间不断受到挤压的情况下，许多数学教师顺应高职教育的发展，开始了高职数学“模块化”之旅．近十年，它受到了高职数学教师的普遍关注，俨然成了高职数学课程建设的显学[3]．

2 高职数学“模块化”之缺陷

2.1 “模块化”及其现状

“模块”是一个源于建筑、家具、计算机等行业的术语，它有3个基本内涵[6]：①它是一个部件、组件，其大小介于整体与零件之间，是整体的基本组成部分，离开了整体，模块也就丧失了存在的意义；②每个模块本身是独立的，可以将其进行不同的组合；③每个模块都是标准化的，有严格的指标要求，否则就无法对模块进行不同组合．将这个概念引入到课程领域之后，“模块”就被理解为一种相对独立的、标准化的教学单元或“教学包”，它有自己明确的起点和终点．而“模块化”则是对原有课程内容进行分解，直至获得所需模块的过程．石伟平教授认为：“如果把课程内容分解成一个个小的单元，每个单元独立设为一门课程，并对其进行标准化，即开发模块课程，那么当新技术出现时，只要适当增加、减少或更换其中的一些模块，便可满足技术革新的要求．同时，学员也可根据自己的需要选取一些模块，组成适合自己的个性化课程计划．”[6]如此就能实现“模块化”主要目的：增强课程的灵活性，激发学生的学习动机．

中国高职数学模块化的兴起有两个主要原因，一是受20世纪90年代以来职业教育课程发展思潮的影响，二是对1999年教育部颁布的《高职高专教育高等数学课程教学基本要求》中所提出“必需、够用”原则的一种响应．高职数学模块化正好顺应了这个时代的要求．其结果是产生了两大模块：公共基础和专业选修[1~2，7~8]．公共模块是各个专业普遍适用的，以一元函数微积分为主；选修模块是根据不同专业要求分解出来的限选模块．比如，电气电子类选修“常微分方程”、“拉氏变换”和“傅里叶级数”等模块，经济管理类选修“线性代数”、“线性规划”和“概率统计”等模块．事实上，许多学校只是把原来的高等数学进行了归类和重整，冠以一个模块的名称，而细看其课程内容，与原来的“压缩型”课程并没有什么差别．这是高职数学课程模块化的基本现状．

确实，高职数学“模块化”在某种程度上满足了不同专业对教学内容的选择性要求．但是，“模块化”论者并不以此为归依，而是期望对“压缩型”课程的痼疾动手术，实现高职数学的应用性．众多标名为“工程应用数学”或“经济应用数学”教材正是希望通过名称变化向人们传达“工具性”课程意图．遗憾的是，纵览这些教材或模块，其中的数学知识仍然是去情境化的、纯粹的，与“压缩型”没有本质差别．它们不仅很少涉及工程或经济，应用也讲得微乎其微，可以说是“有名无实”．这与“模块化”的追求相距甚远．于是怀疑，“模块化”能实现不同专业对高职数学工具性的诉求吗？

2.2 高职数学“模块化”困境

从理论上看，任何的课程内容都可以模块化，但并不是所有的课程都需要模块化．比如，《大学语文》、《道德与修养》等课程比较适合于模块化，因为这些学科或课程的知识本身没有内在的逻辑关系，知识的选择、组织比较自由，是一种“弱度框架”课程．而数学是一个逻辑严密的知识系统，是一种“强度框架”课程．对数学课程进行“模块化”或者让学生选择所需模块进行学习，必须考虑各个模块之间的逻辑顺序．例如，“常微分方程”与“拉氏变换”表面上看似乎是两个独立的模块，然而，拉氏变换在电路分析中最重要的应用是将时域的常微分方程转变为频域的代数方程，所以将它们纳入一个课程系统之中时常采取“常微分方程”+“拉氏变换”的顺序，也就是说，逻辑仍然是隐藏在“模块化”之下一条不可背离的暗线．事实也正如此，高职数学“模块化”只是把相对独立的内容作为选择性模块，并对这些模块进行形式结构上的重组，这种“模块化”的比较优势在哪里呢？最近，有人对全国十省市高中数学模块化课程的实施情况进行调研，发现模块化的课程理想与教学实践之间存在着非常明显的背离[9]．多数（50%以上）受访教师和教研员并不认同模块化，因为它肢解了数学知识的逻辑结构和有机联系，导致了教学内容的重复或脱节，增加了师生的教学负担．这个结论对高职数学“模块化”是有启发的．

从实践看，“模块化”在贯彻工具性思想过程中存在着显见的困难．比如，“定积分”是“基础模块”中重要内容之一，是经济管理类和电气电子类必须要学习的．“模块化”论者对其采取的是普适性与理论化的处理，并没有体现出针对不同专业背景进行知识应用的教材设计．对电气电子专业来说，不结合电压、电流、电感、电容等概念之间的关系，以及电感（或电容）存储和释放能量的过程，学生如何能有效地理解定积分在专业应用中的意义和价值呢？对经济类专业来说，不结合消费者（或生产者）剩余、净投资与资本存量、连续年金的现值等概念，学生也难以领会定积分的真正作用．也就是说，即使是比较简单的定积分，融通专业知识之后的教学文本必然会有相当大的差异，因为“电子”与“经济”毕竟是两个不同专业的话语系统．由此类推，不同类别专业的同一主题（如函数、导数及其应用、常微分方程等）的教学文本的组织与编写也肯定存在着相当多的差异．高职数学不应该也不能忽视这种差异，并且必须在课程文本中积极地反映出这种差异，因为它表征了抽象数学知识在不同专业之中的应用状态，这种状态正是高职数学所需要的．在“模块化”框架下处理好这种差异，以便让不同类别专业的师生都感到满意，势必会使“模块化”教材累赘不堪．这显然是“模块化”论者所不愿看到的．

可见，“模块化”数学教材很难表现数学与专业应用的有机融合，难以体现数学的工具性价值．从它的编排思想和课程内容上看，目前的高职数学“模块化”并没有突破原来的高等数学知识体系和框架，也就不可能有实质性的创新．

3 高职数学的构建逻辑

在高职数学课堂里，经常会有学生问“数学有什么用？”这是一个很好很合乎情理的提问．说它合乎情理，是因为高职生在过去已经学习了12年数学，一直处于“为考而学”的状态．现在，他们进入了大学，开始关注“为用而学”、以及数学与专业的关系？数学对自己专业发展有什么贡献？说它很好，是因为它一次次地催促研究者思考：高职数学的教育目的是什么？我们教什么？其实，学生的问题应该是“学数学有什么用？”因为作为科学的数学与作为学校教育任务的数学是两个很不相同的概念．几乎没有人怀疑数学科学的价值，李文林先生和任辛喜先生曾在著作《数学的力量——漫话数学的价值》中讲得非常充分[10]．但是，在中国，经过学科专家、学者编撰的学校数学（或数学课程）的价值却饱受质疑，其中最为大家诟病的是学校数学工具性缺失．2013年某网站关于“数学退出高考”调查的一边倒结果（73%的支持率）在某种程度上表达了参与调查的公众对学校数学教育的强烈不满．这也从一个侧面说明，把拥有几千年历史积淀的数学科学编撰为不同类型学校的数学课程时，总是会遇到比著名课程论专家泰勒（R. W. Tyler）在《课程与教学的基本原理》一书中所描述的课程编制方法和步骤还要繁复的过程，因为其中隐藏着许多看不见的思想观念的碰撞与冲突．显然，在这件事情上，并没有比其它国家和地区做得更好．

回到高职学生的问题，学校数学教育的用处无非是两个：一是“虚用”，二是“实用”．虚用指发展学生的数学思维或培养数学素养．这种作用不一定能在短期内培养和显现出来，但它是个体成长与发展的基础；实用是指非数学专业的其他人员（包括在校的各级各类学生）所体验到的实际与实在的用处，也就是学校数学的工具性．那么，“虚用”与“实用”之间有什么关系呢？

第一，从中国高职数学的教材体系、内容结构看：“虚用”有余，“实用”不足．有人认为，职业院校学生的数学素养比较差，需要多花些时间学习数学，以提高他们的逻辑思维能力和数学素养，因为这种数学素质对他们一生的发展都有极大好处．这种强化“虚用”的出发点和愿望是良好的，但效果往往很不好．首先，不得不面对的事实是，高职生中的相当一部分就是因为高考数学成绩不理想才进入职业院校的，他们在12年数学教育中都没有形成良好的数学素养，研究者却想在3年职业教育之中将其提升起来，这究竟是相当困难还是确实容易呢？如此这般，是不是会陷入恶性循环？许多高职院校之所以大量削减数学课时，原因是多方面的，但其重要原因之一就是高职数学在不断地强化学生的失败感，导致数学教学到了难以实施的程度．其次，理论性强，知识点多，容量大，要求高一直是中国大学高等数学教学的基本特征[3]，这也是导致大量学生数学学习失败的主要原因．如果高职数学仍然坚持理论性教学，学生必然继续面临数学学习的窘境，学习积极性进一步受挫，导致他们愈加不喜欢数学．然而，通过加强与专业的联系，突出数学应用，可以在某种程度上克服数学知识的抽象性，这既实现了为专业服务，也适合高职生的学习特点．再次，学校数学对思维训练有重要作用，数学素养也是一种基础素质．这不仅得到了众多数学家、哲学家的广泛认可[11]，而且延续至今的西方科学与文明的发展史也表明了这一点．但是，在某些时候与场合，这种作用和素质在数学教育实践中被无限地放大了，认为它是可以跨越不同领域解决问题的“原始智能”，以至于学校不同阶段、不同类型数学教育在教学内容、方法和要求上都遵循着一种“高标准”信念：“数学教育是培养数学家的教育．”[12]这也曾是荷兰数学教育家弗赖登塔尔先生对数学教育的担心．在与众多的同行进行交流时，研究者发现，这些老师总是希望通过（高职）数学教育来培养（或解决）学生终身发展所需要的思维能力（的问题）．现代多元智能理论的创始人、著名美国心理学家加德纳并不认同这种观点，他说：“这种智能在其它地方，却没有那么重要……按照我的思维方式，将逻辑—数学智能看作是一组智能中的一种智能，认为它是一种能处理某类问题的威力巨大的技能，但绝不比其它智能优越，绝不危险地认为它能压倒其它智能，似乎要合理得多．”[13]

同时，这种观点所隐含的教育思维方式也值得商榷．在终身教育时代，人们的生活和学习模式发生了根本变化，即由线性模式转向循环模式．在线性模式中，人的一生是按照先学习、后工作、再结婚的顺序进行的；在循环模式中，人在一生中某个阶段有可能完全抛弃以往的一切，重新开始一种新的学习、工作和生活．因此，数学教育企图为学生准备其一生所需要的数学素养不仅是不可能的、也是荒谬的．而合理的方式是，当他们确实感到需要的时候，再及时给他们提供相应的教育．这时的数学教育会因为个体强烈的学习愿望和丰富的工作经历而达到事半功倍的效果．

第二，基础性和工具性是描述数学课程的一对范畴，它们并不是完全对立的．“基础性”有两个考察维度：“基本性”和“发展性”；前者是对后继的知识体系建构而言的，后者主要是对学生思维能力培养而言的．“工具性”的考察维度是“能用性”．过去，有相当多的数学教师囿于自己的学科身份、职业角色和知识视野等诸多原因，没有处理好基础性与工具性的关系，或将它们看成对立面，用“基础性”排斥“工具性”，或将它们等同起来，用“基础性”代替“工具性”，由此导致不同教育阶段对数学课程工具性的忽视．现在，要思考“这门学科对教育那些不想专于此业的年轻人有什么贡献？”[14]要重新估计数学的工具性价值．也许有人认为：强调数学为专业服务，突出应用性会弱化数学培养思维素质的功能．这种说法是不能成立的，因为两者之间并不存在必然关系．高职数学教育功能的发挥主要取决于两个方面：一是教学材料或内容的特征．实施高职数学与专业结合的方式，在理论数学中融入相关专业的知识、问题、情境和案例，把数学的应用性体现出来，这样做并没有抽掉高职数学所具有的抽象性和逻辑性．也就是说，培养学生思维素质的逻辑基础依然存在；二是课堂教学目标与方法．实际上，数学思维能力的培养可以在脱离专业应用的、纯粹的数学环境里进行，比如，平面几何就是培养学生逻辑思维的相对纯粹的载体．但是，运用数学解决应用问题所需经历的建模和求解过程，这其中可能没有数学思维的参与吗？相反，数学应用是一种高级的综合能力，它并不比单纯地掌握知识和法则来得更简单；人们只要回忆小学里求解算术式子题和应用题的过程和经历就明白这一点．而当把培养应用能力作为高职数学教学目标时，为什么有人怀疑这样会弱化思维训练的功能呢？再者，训练思维、发展思维能力的目标又是什么呢？究其原因，这与他们头脑中所固有的非此即彼的“二分法”有关．与专业结合、为专业服务的高职数学，只是采取了与过去不同的教学内容或方式，达到应用能力的培养目标．这是使忽视应用的高职数学教育回到它的正道上来．

第三，“必需、够用”是高职课程建设的一个通用原则．这个原则经历了较长时间和不同学科的检验，有一定合理性，但它主要针对教学内容的深度和广度而言，不可能详细指导各门具体课程的内容组织和编排方式，因为每一门课程都有其自身的特点和教学要求．比如，对高等数学中的定积分而言，教学它的概念和基本运算就符合了“必需、够用”原则．然而，在多数情况下，学生并不知道自己专业里的哪个地方需要用这个概念，以及如何用这个概念．这表明，只有“必需、够用”原则，还不能解决高职数学的应用问题．于是有必要扩展和增加新的原则，通过这个新原则把纯粹数学落实为工具性数学．简单地说，这个原则就是“能用性”．它是对“突出应用性，与专业结合，为专业服务”思想、以及把数学作为理解和解决专业技术问题的普遍性工具的简明概括．它是决定高职数学课程内容的组织与编排的一个重要原则．落实“能用性”就是要在数学教材中把数学知识之用以适当的形式展示出来，让学生真正地看到数学是如何应用的．这个原则对高职数学具有重要意义，因为高职数学如果不体现这一点，就可能重蹈“压缩型”的覆辙．这是高职数学区别于本科数学的重要特征．

同时，贯彻“能用性”还应该是普遍的．比如，在电气电子类要讲向量变换法、复数的阻抗，要用定积分分析电路中能量的存储与释放，用微分方程讨论电路的阶跃响应和固有响应．否则，学生就不可能学会用定积分和微分方程去分析和解决具体的专业问题．以前，这种“混合状态”知识属于两个不同的课程、分别由数学和电子两个专业的不同教师来完成，现在则由数学教师在数学课程里来完成．采取这种不同于“压缩型”处理方式的意义在于：一方面，它有利于激发学生的学习动机．过去，偏重“虚用”的老师常常对学生说“以后总是会有用的”，企图让学生在其生命成长过程中以邂逅的方式去体会数学的应用价值．这是一种非常错误的想法．著名数学家、哲学家、教育家怀特海（Whitehead, A. N）说：“不管学生对你的课程有什么样的兴趣，这种兴趣必须在此时此刻被激发；不管你要加强学生的何种能力，这种能力必须在此时此刻得到练习；不管你想怎样影响学生未来的精神世界，必须现在就去展示它．”[15]许多高职生正是因为看不到数学有什么用而不愿意学数学．另一方面，它还建立了数学知识与专业应用之间的联结．有时，把数学应用看得过于简单，认为它不如纯粹理论重要，以至对它采取一种漠视的态度．其实，建立数学与相关专业的联系，以及加强对数学结果的解释等这样一些过程对高职生来说不仅是必需的，而且也不是轻而易举的，甚至是复杂的．

加强高职数学的应用性必须融通其它专业（如计算机类、电气电子类、经济管理类）的相关知识，这需要尝试从非数学专业的学科专家那里获得“教什么”的支持．即是，高职数学必须由不同专业领域里的学科专家，通过研讨与协商的方式，对课程内容做出选择，这样的建构逻辑对高职数学教育是十分必要的．反观高职数学“模块化”，它仍然局限于“压缩型”思维和“必需够用”原则，而没有跳出传统的高等数学框架，进行跨学科的思维，只能滑入“压缩型”窠臼，其课程愿景最终也成了镜中花、水中月．

当然，体现“能用性”原则的课程文本必然会呈现出相当鲜明的专业特色，这种特色是不同类别专业的数学课程相互区别的重要标志．这揭示了一条崭新的高职数学课程建设之路——类别化．

4 高职数学课程类别化

4.1 类别化及其方法

数学是抽象的，但数学的应用却是相对具体的．它普遍存在于高职院校的经济管理、电气电子、计算机技术、机械制造等专业课程之中，并以解决相关专业问题的方式来呈现．根据不同类别专业对数学知识的需求，实现数学与不同专业的有机融合，构建具有专业特色的应用性数学课程的过程，这就是高职数学“类别化”．

与传统“压缩型”和“模块化”不同，类别化具有如下特点：一是专业针对性．不同的职业技术需要不同的数学，不同类别的专业学习不同的数学．鉴于类别化的繁重压力和超大工作量，可以先考虑针对一些专业大类，如计算机技术类、电气电子类、机械制造类、经济类、管理类等进行类别化，分别构建《计算机数学》、《电路数学》、《机电数学》、《经济数学》、《管理数学》等课程．二是知识应用性．在体现针对性的基础上，通过专业实例和问题，把相关专业对数学的要求和方法普遍地融合到高职数学之中，让学生看到数学有用、能用，感受数学的工具性力量．简单说，就是根据专业的需要讲数学，用专业的例子讲数学．表1揭示了“压缩型”、“模块化”、“类别化”的课程特点及其适用范围．

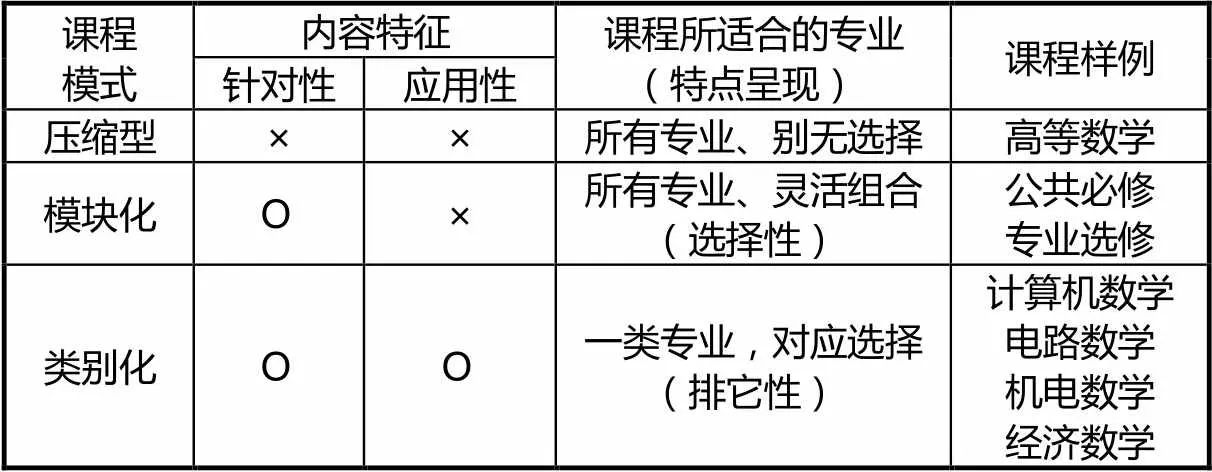
表1 课程特点及其适用范围

注：其中×表示没有，О表示有

从理论上讲，在“类别化”基础上可以再进行“模块化”，但此时“模块化”已经失去了模块化的功能，因为课程的类别化已经使其在专业适用性上具有排它性，“模块化”没有了意义．比如，经济管理类“函数”经过类别化之后，包括需求、供给、收入、成本、利润、生产、指数、对数等函数，若再进行“模块化”，意欲何为呢？同理，“模块化”之后也可进行“类别化”，但现实中谁又会费神去虚晃“模块化”一枪呢？正如前文所述，“模块化”本质上只有标签意义．从课程文本和课程实施上看，模块化与类别化的根本区别就在于课程内容的排它性，因为不同类别之间的同一个教学主题是旨趣大异的．

类别化的高职数学已经不再是传统意义上“可有可无”的公共课或平台课（比如《大学语文》或传统《高等数学》），而是学好专业技术所必需的专业基础课．它类似于美国、加拿大等西方国家的社区学院所开设的《技术数学》．只有这样，数学课程才能达到使学生“具有系统的应用知识和持续发展的能力”这个要求，才能确立它在职业技术能力发展中的必需地位．

基于上述比较和“模块化”工具性困境之分析，高职数学从“模块化”转向“类别化”是实现数学工具性、体现数学应用价值的必然选择．

高职数学“类别化”有两个步骤．第一，了解相关专业的数学需求，形成类别化的基本素材．通过与专业教师座谈、查阅相关专业的教材，了解到不同专业对高等数学有着十分不同的需求．比如，计算机技术专业对离散数学和算法的需求较多，对传统微积分的需求较少；电气电子专业需要较多的微积分；机械制造则需要较多的三角函数和解析几何．于是，响应了不同类别专业的要求，“固本拓边”地扩展了自己的学习领域，深入了解相关专业的知识，如计算机专业的C语言、数据库和电气电子的电路分析等，并在数学与相关专业要求之间寻求结合点．过去，有些教师曾开展过理工类、经济类专业的数学需求调查，完成了许多繁杂工作．但是，他们寻找的是不同类别专业的公共需求，追寻的是不同专业的教学内容之共性，最终走向了“模块化”．与其不同，研究者更多地追求不同类别的数学内容之个性，并把个性之表现作为数学课程建设的必要成分，这样就走出了一条异于“模块化”的高职数学“类别化”道路．第二，建构应用性体系的高职数学．其实，“压缩型”高职数学之中也有一些应用实例，但这种应用只是一种点缀与装饰，没有专业针对性，基本丧失了工具性作用．而“类别化”是根据相关专业的特点，广泛地挖掘和收集丰富典型的应用性素材，组织和编制出符合专业应用性要求的数学课程．泰勒认为，有效地组织学习经验有3个标准，“即连续性、顺序性和整合性”[15]．前两个标准在一定程度上体现了数学的逻辑性，而“整合性是指课程经验的横向联系”，这正是“类别化”所强调的不同类别专业知识与数学的融合．可见，坚持这3个标准对“类别化”课程建设仍然具有现实的指导意义．

4.2 类别化之实践

根据上述步骤，研究者用8年（2009—2016）时间开发了适用于计算机技术类专业的《计算机数学》[16]、电气电子类专业的《电路数学》[17]、机械加工类专业的《机电数学》[18]、经济类专业的《经济数学》[19]．比如，在《计算机数学》中，研究者摒弃了传统的微积分，而把数的进制、集合与关系、算法基础、图论与树等作为计算机数学的主体，这与其它命名为《计算机数学》教材有相当多的不同．在《电路数学》中，大胆地突破了传统的高等数学框架，选择了函数、向量与复数、导数法、积分法、常微分方程、拉普拉斯变换、傅里叶级数、行列式与矩阵等主题，其中各章节的内容更是体现了电类专业的鲜明特色．比如，把不同电路产生的正弦波作为函数的一种类型；在向量与复数中介绍电路分析中的重要方法——向量变换法，并用以讨论复数阻抗；结合不同元件的电路，运用定积分分析电路元件的储能或放能的状态．显然，诸如此类的多种融合完全不同于以往的“压缩型”和“模块化”，它让学生看到了数学在解决专业问题中的作用，感受到了数学与专业技术之间的关联．

尽管“类别化”高职数学实现了“突出应用性，与专业结合，为专业服务”的课程愿景，有效地支持着相关专业的课程学习，但它要求教师跳出既定的高等数学框架、进入到自己并不擅长的专业领域，这对许多高职数学教师来说都是一个挑战．因此，对专业应用感兴趣的数学学科专家应该积极投入高职数学类别化课程建设之中来．尽管高职数学“类别化”过程比较艰辛，已经取得的局部成果暂时还没有在全国普遍推广开来（因为它“有难度”、“不好教”），但研究者希望通过自己的努力，能够促成高职数学类别化思想的兴起．

[1] 云连英．面向专业需求的高职数学课程设置研究[J]．数学教育学报，2008，17（4）：73-76．

[2] 邹成．高职数学课程的模块化建设[J]．职业与教育，2013，（17）：138-139．

[3] 游安军．反思中国高职院校的数学课程建设[J]．数学教育学报，2015，24（2）：98-100．

[4] 戴士弘．职业教育课程教学改革[M]．北京：清华大学出版社，2007．

[5] 丘成桐．数学与教育[M]．北京：高等教育出版社，2011．

[6] 石伟平．职业教育课程开发技术[M]．上海：上海教育出版社，2006．

[7] 陈伟，李浩．高职数学课程模块化研究[J]．职业技术教育，2009，（11）：21-22．

[8] 黄映玲．高职数学模块化教学探究[J]．高教探索，2010，（1）：89-91．

[9] 于波．高中数学模块课程实施的阻抗研究[J]．课程·教材·教法，2013，（2）：40-43．

[10] 李文林，任辛喜．数学的力量[M]．北京：科学出版社，2007．

[11] 莫里兹．数学的本性[M]．朱剑英译．大连：大连理工大学出版社，2008．

[12] 弗赖登塔尔．作为教育任务的数学[M]．上海：上海教育出版社，1995．

[13] 霍华德·加德纳．智能的结构[M]．沈致隆译．杭州：浙江人民出版社，2013．

[14]  R·W·泰勒．课程与教学的基本原理[M]．罗康等译．北京：中国轻工业出版社，2008．

[15]  A·N·怀特海．教育的目的[M]．庄莲平译．北京：文汇出版社，2010．

[16] 游安军．计算机数学[M]．北京：电子工业出版社，2013．

[17] 游安军．电路数学[M]．北京：电子工业出版社，2014．

[18] 游安军．机电数学[M]．北京：电子工业出版社，2016．

[19] 游安军．经济数学[M]．北京：电子工业出版社，2016．

Curriculum Paradigm of Higher Vocational Mathematics: from Modularity to Classification

YOU An-jun1, CAO Guang-fu2, YANG Yu1

(1. Zhuhai City Polytechnic Institute, Guangdong Zhuhai 519090, China;2. Institute of Mathematics and Information Science, Guangzhou University, Guangdong Guangzhou 510006, China)

In recent 20 years, we had had some important changes about the vocational mathematics, which were the transfers from foundation to application, i.e. application of mathematics, the mixture with related specialties, and service to related specialties were emphasized in mathematics curriculum. These were the features of vocational mathematics. So as to achieve these demands, the transfers of mathematics curriculums were undergone from compressed form to modularity, but the applied function of vocational mathematics curriculum couldn’t be achieved in the blocked curriculum. As long as we had escaped from modularity and thought deeply between the different specialties, and developed the construction of classified curriculum, the applied function of mathematics could be achieved. Classified mathematics curriculum could express the ideas, which mathematics curriculum gave service to specialties and students.

vocational mathematics; curriculum paradigm; compressed curriculum; modular curriculum; classified curriculum

[责任编校：周学智]

G420

A

1004–9894（2017）04–0092–05

2017–03–06

珠海城市职业技术学院教研科研重点课题——高职数学课程类别化的理论与实践（20151210）

游安军（1965—），男，湖北嘉鱼人，教授，教育硕士导师，主要从事数学课程与教学论和职业教育数学课程研究．