中美高等数学教材内容的比较研究——以美国宾夕法尼亚九版和中国同济七版为例

田仕芹，王玉文



中美高等数学教材内容的比较研究——以美国宾夕法尼亚九版和中国同济七版为例

田仕芹1，2，王玉文1

（1．哈尔滨师范大学教育科学学院，黑龙江哈尔滨 150025；2．常熟理工学院数学与统计学院，江苏常熟 215500）

采用定性和定量研究相结合的方法，对宾夕法尼亚九版和同济七版高等数学教材进行比较分析．研究发现：两版教材内容体系编排及难度差别较大．同济七版注重数学知识体系的系统性和数学理论的严密性，习题侧重纯数学问题；宾夕法尼亚九版注重数学直观、现实应用和学习指导，习题侧重有真实数据来源的实际问题．同济七版的总体难度高于宾夕法尼亚九版．在共有内容中，同济七版的知识点数量是宾夕法尼亚九版的1.3倍；同济七版在基础性知识、微分和积分3个知识团的内容深度与习题难度均高于宾夕法尼亚九版．建议在教材的编写中，体现高等数学在学科中的应用价值、适当增加直观呈现、注重数学知识的生成过程、融入学习指导．

高等数学；教材；内容；难度；比较

1 问题提出

系统性、抽象性、应用性很强的《高等数学》作为高校的一门基础课程，教材内容编排及难度高低直接影响到学生数学素质的提高和相关专业课程的学习．中央电视台播出的一期《开讲啦》节目中，在开讲嘉宾樊纲教授与观众交流互动环节，复旦大学经济系的一位大一新生提出这样一个问题：“作为经济学的必备基础，高等数学……对于我们来说真的是很困难……您怎么看待这些非常恶心的数学工具？”究竟是什么原因使学生觉得高等数学难学，甚至用“恶心”来形容？是否因为高等数学教材内容真的太难？如果难，具体难在哪些方面？又该如何改进？

国内对数学教材难度的研究取得了不少有意义的结果[1~12]，但对高等数学教材难度的研究较少，目前能查到的高等数学教材难度研究的文献只有文[4]．已有研究集中于中小学数学教材方面，且主要是数学教材难度模型的构建和教材难度的比较，孔凡哲等在文[12]中建立课程难度定量模型，、、、分别表示课程难度、课程深度、课程广度和课程时间，其中，被称为加权系数，满足0<<1．邝孔秀等在文[7]中构建小学数学教科书难易程度的数学模型，、、分别表示内容广度、内容深度和习题难度，、、为相应的权重．基于高等数学课程教学基本要求，高等数学教材的编写和修订主要从内容深度、内容广度和习题3个方面进行，参考文献[7]中的教材难度模型，选取教材内容广度、内容深度及习题难度3个维度，建立高等数学教材难度模型，并遵循系统优化原则，组织同行专家进行分析对比，采用统计平均法确定各维度的权重．鉴于在高等教育领域，美国有着较为先进的教育理念，通过对美国宾夕法尼亚九版和中国同济七版高等数学教材的比较分析，明晰两版高等数学教材在内容选择、编排、呈现、难度等方面的差异，拓展高等数学课程建设中的教材编写思路，优化教材的结构体系，为高等数学教材编写提供新的案例参照，进而为教师和学生提供更适合的教材．

2 研究设计

2.1 高等数学教材的选取

选取的美国高等数学教材为（Ernest F. Haeussler, Jr. Richard S. Paul. The Pennsylvania State University. Prentice Hall InternationalInc, Ninth edition. Simon & Schuster A Viacom Company Upper Saddle River, NJ 07458），共I、II、III三册，以下简称宾夕法尼亚九版，适用于普通高等院校的商业、经济、生命和社会科学等专业．据研究者调查了解，国内不同院校的商业、经济、生命和社会科学等专业所用的高等数学教材不一，有些院校用的是同济大学数学系编的《高等数学》，有些院校用自编教材，如复旦大学经济学院用的是宋礼民等主编的《高等数学》．由于同济大学数学系编的《高等数学》是国内使用量大、适应面广的优秀教材，其它不同版本的高等数学教材内容体系与同济大学数学系编的《高等数学》基本一致，因此国内高等数学教材选取《高等数学》（同济大学数学系编，高等教育出版社，第七版），共上、下两册，以下简称同济七版．

2.2 研究方法和工具

研究采用定量和定性相结合的方法．

定性分析方面，主要是两国教材整体内容框架、呈现形式、习题、特色内容方面的比较．

定量研究方面，选取教材内容广度、内容深度及习题难度3个维度，参考文献[7]建立教材难度模型

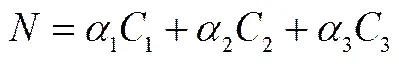
内容深度和习题难度的维度及水平划分如表1所示．

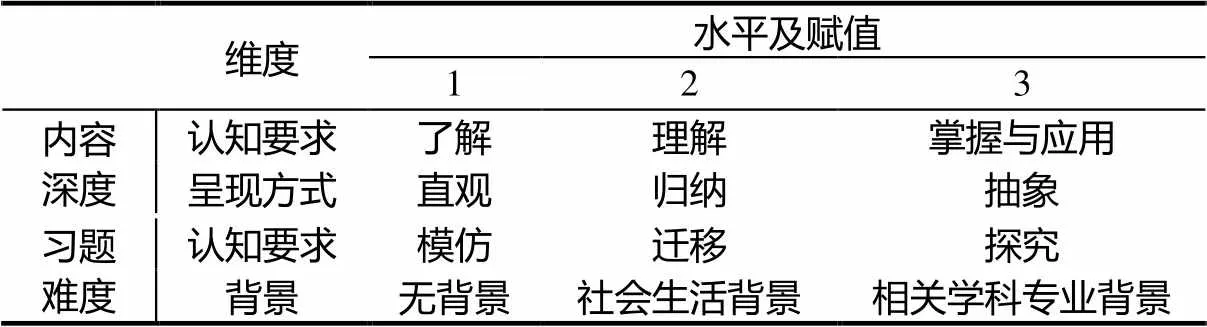
表1 内容深度和习题难度的维度及水平划分

3 结果与讨论

3.1 中美高等数学教材内容的整体比较

（1）内容框架．

中美高等数学教材各章节内容如表2所示．

表2 中美高等数学教材各章节内容

①整体上：两版教材体系编排差别较大．

②基础性知识部分：宾夕法尼亚九版函数内容比同济大学七版详细得多，极限内容两本教材占各一章，同济七版更注重严密的理论基础和理论说明、证明，宾夕法尼亚九版更注重借助图象或数据帮助读者理解并得出结论．

③微分部分：同济七版安排了4章，宾夕法尼亚九版安排了5章．导数、微分概念及其应用部分，同济七版在曲线的凹凸与拐点、曲率、方程的近似解、全微分的应用、微分法在几何上的应用等内容上，都做了比较详细的介绍和讲解．宾夕法尼亚九版将对数函数的微分、指数函数的微分、隐式微分、对数微分和高阶导数的内容作为一章；曲线作图单独作为一章；微分的应用单独作为一章，内容主要有最大值和最小值的应用、微分、需求弹性、牛顿法．中值定理的内容，在同济七版中单独作为一节，教材从罗尔定理到拉格朗日中值定理到柯西中值定理，自上而下的定理由来环环相扣、步步深入，逻辑结构鲜明紧凑，而在宾夕法尼亚九版中未做详细介绍．同济七版将微分方程单独作为一章，而宾夕法尼亚九版未有这部分内容．较之国内教材内容体系的缜密严谨，宾夕法尼亚九版内容更细致、更注重应用．

④积分部分：同济七版安排了5章，宾夕法尼亚九版安排了3章，同济七版更注重数学知识的系统性和理论的严密性，宾夕法尼亚九版更注重应用性，以运算、数据来得出和说明结论．

⑤其它内容：同济七版安排了空间解析几何与向量代数、无穷级数．宾夕法尼亚九版安排了矩阵代数、线性规划、金融数学、概率和统计、概率的附加专题、连续随机变量．事实上，线性代数和概率统计在中国是单独作为一门课程来安排的．

（2）内容呈现形式．

教材内容的呈现形式多种多样，除了文字这一主要呈现形式以外，还有公式、图表、图形等辅助呈现形式，同济七版和宾夕法尼亚九版在微分和积分模块的配图数如表3．

表3 中美高等数学教材共有模块配图数

由表3可以看出，宾夕法尼亚九版用了大量的图表和图形，数形结合，直观清晰，这种多图呈现方式使教材理论更易为学习者接受，激发学生的学习兴趣，提高学习自主性．

（3）习题．

从教材习题来看，宾夕法尼亚九版题量大，题型丰富，注重应用．每一小节结束后有概念题、常规计算、应用题、探索题等，每章结束后有复习题、情境题（Mathematical snapshot形式）等，特别是教材中里的应用题涉及社会生活的方方面面，且列出了应用题的数据来源．相比较而言，同济七版习题更侧重于应用数学定理和公式去解决纯数学问题，讲究解题技巧，应用性问题主要涉及微积分在近似计算中的应用和积分学在物理、力学方面的传统应用，难以使学生体会到高等数学的应用价值．

（4）学习指导．

从教材对学生的学习指导方面来看，宾夕法尼亚九版中有具体问题解决方法和策略的指导，如导数部分给出求导策略，同时在每章之后都有内容回顾（Review），列出重要的数学术语和符号、内容概要．同济七版在这方面有待加强．

根据上述两部教材的内容框架分析，以下对教材总体难度、内容广度、内容深度及习题难度的比较分析主要从基础性知识、微分和积分3个知识团来进行．

3.2 中美高等数学教材的总体难度分析

依据教材难度模型，对同济七版和宾夕法尼亚九版各个维度的指标进行赋值计算，结果见表4．

表4 中美高等数学教材难度比较

结果表明，同济七版的总体难度高于宾夕法尼亚九版，且同济七版在内容广度、内容深度和习题难度上均高于宾夕法尼亚九版．

具体地，同济七版和宾夕法尼亚九版基础性知识团的难度分别为0.692、0.595，微分知识团的难度分别为0.778、0.635，积分知识团的难度分别为0.741、0.612．同济七版在各知识团的难度都高于宾夕法尼亚九版．

3.3 中美高等数学教材的内容广度分析

同济七版和宾夕法尼亚九版各知识团的知识点分布情况如表5．

表5 中美高等数学教材内容广度比较

从表5可以看出，同济七版基础性知识、微分和积分三知识团的知识点数量均大于宾夕法尼亚九版．总体上，同济七版的知识点数量是宾夕法尼亚九版的1.3倍，两版教材的知识点交集较大，有55个共有知识点．

3.4 中美高等数学教材内容深度分析

中美高等数学教材的内容深度比较如图1和图2所示．

图1 中美高等数学教材的内容深度（不同知识团）

图1表明，同济七版基础性知识、微分、积分各知识团的内容深度均高于宾夕法尼亚九版，两版教材分别在各知识团的内容深度相对均衡．

从“认知要求”及“呈现方式”两个维度对两版教材的内容深度进行分析，在认知要求上，同济七版和宾夕法尼亚九版的深度分别为0.762和0.597，其中同济七版认知要求为“了解”、“理解”、“掌握与应用”的比例分别为7.1%、21.3%、71.6%，宾夕法尼亚九版对应比例分别为8.8%、22.5%、68.7%，两版教材都以掌握和应用为主．在呈现方式上，同济七版和宾夕法尼亚九版的深度分别为 0.682和0.575，其中同济七版呈现方式为“直观”、“归纳”、“抽象”的比例分别为9.2%、6.3%、84.5%，宾夕法尼亚九版对应比例分别为77.3%、9.1%、13.6%，同济七版以抽象呈现为主，宾夕法尼亚九版以直观呈现为主．

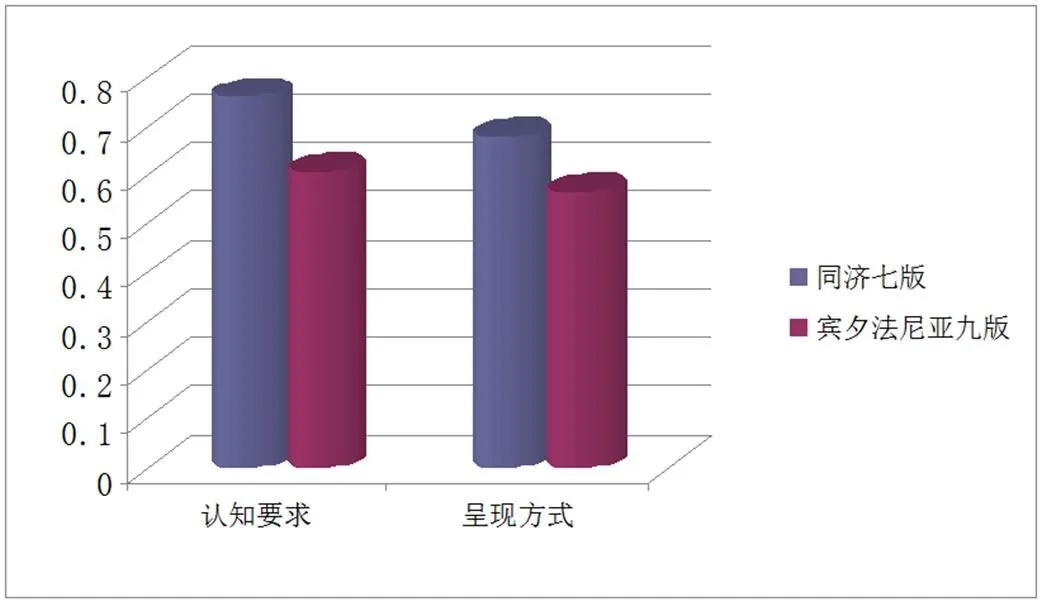
图2 中美高等数学教材的内容深度（不同维度）

3.5 中美高等数学教材习题难度分析

中美高等数学教材的习题难度比较如图3和图4所示．

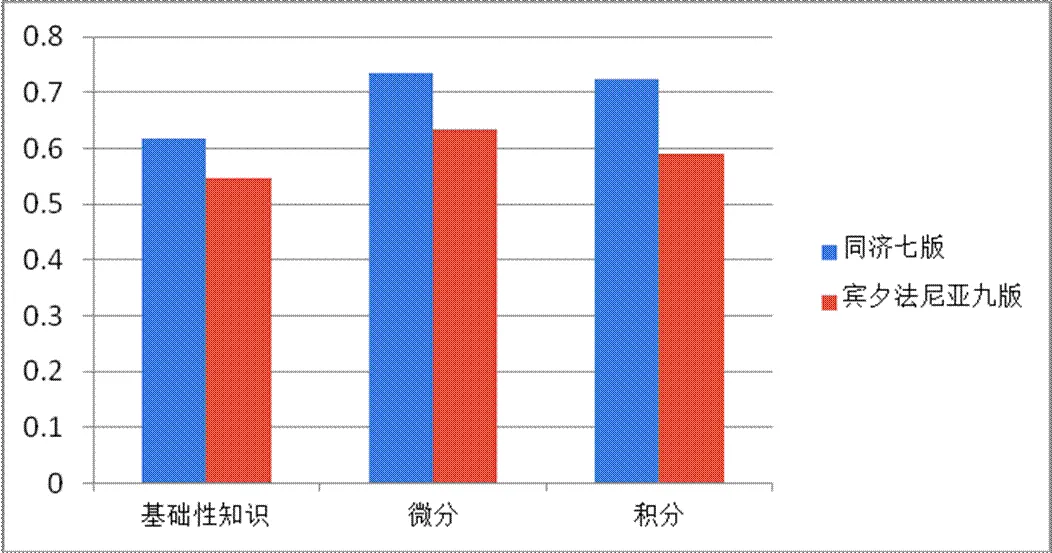
图3 中美高等数学教材的习题难度（不同知识团）

图3表明，同济七版基础性知识、微分、积分各知识团的习题难度均高于宾夕法尼亚九版，两版教材分别在各知识团的习题难度相对均衡．

从“认知要求”及“背景”两个维度对两版教材的习题难度进行分析，在认知要求上，同济七版和宾夕法尼亚九版的深度分别为 0.752 和0.592，其中同济七版认知要求为“模仿”、“迁移”、“探究”的比例分别为21.8%、55.7%、22.5%，宾夕法尼亚九版对应比例分别为24.7%、56.2%、19.1%，两版教材都以迁移为主．在习题背景上，同济七版和宾夕法尼亚九版的深度分别为0.580 和0.655，其中同济七版呈现方式为“无背景”、“社会生活背景”、“相关学科专业背景”的比例分别为85.4%、5.7%、8.9%，宾夕法尼亚九版对应比例分别为13.1%、54.3%、32.6%，同济七版以无背景为主，宾夕法尼亚九版以社会生活背景和相关学科专业背景为主．

4 结论与讨论

4.1 结 论

（1）两版高等数学教材内容编排差别较大．在共有内容中，宾夕法尼亚九版基础性内容比同济七版详细得多；微分模块，同济七版安排了4章，宾夕法尼亚九版安排了5章；积分模块，同济七版安排了5章，宾夕法尼亚九版安排了3章．另外，同济七版还安排了空间解析几何与向量代数、无穷级数，宾夕法尼亚九版还安排了矩阵代数、线性规划、金融数学、概率和统计、概率的附加专题、连续随机变量，而线性代数和概率统计在我国是单独作为一门课程来安排．同济七版更注重教材内容体系的系统性和理论的严密性，宾夕法尼亚九版更注重借助图象、数据或案例等“数学直观”帮助读者理解数学思想并得出结论，同时注重学生学习方法与策略的指导，内容呈现形式较之同济七版更丰富．宾夕法尼亚九版的习题侧重有真实数据来源的实际问题，同济七版的习题侧重纯数学问题．

（2）同济七版的总体难度以及内容广度、内容深度和习题难度均高于美国宾夕法尼亚九版．同济七版的知识点数量是宾夕法尼亚九版的1.3倍，且同济七版基础性知识、微分和积分三知识团的知识点数量均大于宾夕法尼亚九版．同济七版在基础性知识、微分和积分三知识团的内容深度与习题难度均高于宾夕法尼亚九版，两版教材分别在各知识团的内容深度和习题难度相对均衡．在内容的认知要求上，同济七版和宾夕法尼亚九版的深度分别为0.762和0.597；在内容呈现方式上，同济七版和宾夕法尼亚九版的深度分别为0.682和0.575．在习题认知要求上，同济七版和宾夕法尼亚九版的深度分别为0.752和0.592；在习题背景上，同济七版和宾夕法尼亚九版的深度分别为0.580和0.655．

4.2 讨 论

（1）体现高等数学在学科中的应用价值．

比较发现，同济七版的总体难度以及内容广度、内容深度和习题难度均高于美国宾夕法尼亚九版，宾夕法尼亚九版更注重应用，同济七版更注重数学知识的系统性和理论的严密性．一方面，考虑到高等数学知识的整体性和连贯性，不能因为难度大而盲目删减教材内容、降低内容深度和习题难度，正如课程理论专家施瓦布（Schwab J. J.）指出，学科结构对教育具有双重意义：第一，教育工作者在设计课程和准备教材时就必须考虑学科结构，否则课程计划可能被错误地实施，教材可能被误教；第二，一定要把学科结构深入到课程的各个方面，使其成为课程内容的实质，否则就会把学生引入歧图[13]．另一方面，在编写教材时考虑高校不同学科专业对高等数学的需求，加强高等数学教材内容与学科、专业课程的融合，适当增加与学科专业、社会生活相关的背景性知识、实例和习题，并设置运用数学知识、思想和方法解决有关专业问题的探究性课题等，同时给出题目中的数据来源，使学生体验数学与所学专业的密切联系，提高对高等数学在学科中应用价值的认识，促使学生积极投入高等数学课程的学习．

（2）适当增加直观呈现．

研究发现，宾夕法尼亚九版的内容呈现形式更多样化，且以直观呈现方式为主，而同济七版以抽象呈现方式为主，抽象的呈现方式也是导致国内大学生学习数学产生困难的一个原因．数学直观，既是数学抽象思维的问题信息源，又是途径信息源．即使是较为高深、抽象的数学知识，同样需要直观模型，只不过这种直观的层次较高，距离生活直观较远一些，需要相应的基础知识和更多的想象[14]．应借鉴荷兰著名数学教育家弗赖登塔尔的“现实、数学化、再创造”的数学教育思想[15]，适当增加数学直观呈现，如图象、数据或案例等感性材料，降低学生学习抽象数学概念和命题的困难，使思维与直观建立联系，学生在丰富的直观信息的支持下，数学思维被激活，高等数学的学习不再是一种沉重的负担．

（3）注重数学知识的生成过程．

在比较中发现，中国高等数学教材更关注知识的逻辑结构，强调定义的准确性、逻辑的严密性等，对知识的发生发展过程以及学生的主体活动重视不够．数学知识不仅表现为数学概念、定理、法则、公式等陈述性知识，还表现为数学思想方法等程序性知识．在知识的形成和应用过程中渗透数学思想方法，是引导学生体验、感悟数学思想方法的有效策略[16]．教材应充分考虑继承、借鉴、发展、创新的辩证关系，注重数学知识的生成性，为学生“预留”探索与交流的空间，使学生在观察、思考、探究、归纳的过程中，达成对数学知识的“知其源、会其神、通其用”[17~28]．

（4）融入学习指导．

宾夕法尼亚九版中有具体问题解决方法和策略的指导，同时在每章之后都列出重要的数学术语和符号、内容概要，有利于学生自主学习．国内一些学生抱怨高等数学“难学”，教材缺乏一定的学习方法与策略的指导也是其中一个重要原因．为更好地促进学生自主学习，教材编写应关注学生“怎样学”，在教材中融入高等数学学习方法与策略的指导，既可以在具体章节中某个问题解决之前展示问题解决的方法和策略，也可以在教材中专门辟出几个问题解决栏目，配有一定的策略指导，以减少学生在高等数学学习过程中的挫败感和畏难心理，调动学生学习高等数学的自主性．

[1] 鲍建生．中英两国初中数学课程综合难度的比较研究[D]．华东师范大学，2002．

[2] 史宁中，孔凡哲，李淑文．课程难度模型：我国义务教育几何课程难度的对比[J]．东北师大学报（哲学社会科学版），2005，（6）：151-155．

[3] 蔡庆有，邝孔秀，宋乃庆．小学数学教材难度模型研究[J]．教育学报，2013，（5）：97-105．

[4] 赵文才，常正波．高等数学教材难度问题的数学模型研究[J]．兰州教育学院学报，2014，（11）：77-78．

[5] 郭玉峰．中澳高中数学课程难度的量化研究[J]．中国教育学刊，2014，（4）：73-78．

[6] 巩子坤．中德两国小学数学教材难度比较研究[J]．外国中小学教育，2014，（11）：49-56，48．

[7] 邝孔秀．中国小学数学教科书的难度分析[J]．比较教育研究，2015，（9）：73-78．

[8] 严家丽，孔凡哲，李清．中美高中数学教材难度特征的比较研究[J]．上海教育科研，2014，（3）：72-75．

[9] 王建磐，鲍建生．高中数学教材中例题的综合难度的国际比较[J]．全球教育展望，2014，（8）：101-110．

[10] 李欣莲，范涌峰．教材内外“双重难度”探究[J]．中国教育学刊，2015，（12）：44-48．

[11] 张维忠，黄丽虹．新教材“三角形”课程难度的对比分析[J]．数学教育学报，2009，18（4）：61-64．

[12] 孔凡哲，史宁中．现行教科书课程难度的静态定量对比分析[J]．教育科学，2006，（3）：40-43．

[13]  Schwab J J.[M]. H. A. Giroux (ed), Curriculum and Instruction, 1981.

[14] 郭思乐．数学教学中的直观[J]．课程·教材·教法，1986，（5）：40-42，39．

[15] 弗赖登塔尔．作为教育任务的数学[M]．陈昌平，唐瑞芬译．上海：上海教育出版社，1995．

[16] 吴增生．数学思想方法及其教学策略初探[J]．数学教育学报，2014，23（3）：11-15．

[17] 何光峰，李美娟．TIMSS数学录像课研究及其借鉴意义[J]．数学教育学报，2016，25（5）：88-90．

[18] 左敬亮，方勤华，程垚松．美国“数学教师TPACK标准和发展模型”——数学教师有效使用技术的新焦点[J]．数学教育学报，2016，25（2）：44-46．

[19] 田方琳，汪晓勤．美国《数学教师》上的HPM内容分析[J]．数学教育学报，2016，25（4）：42-46．

[20] 陈成钢．“卓越计划”下大学数学考核方式改革的探索[J]．数学教育学报，2015，24（5）：59-61．

[21] 卢建川．美国最新NCATE数学教师职前专业标准评介[J]．数学教育学报，2016，25（4）：47-53．

[22] 朱长江，李书刚，胡中波．在数学文化课程中引进优质教学资源开展混合式教学的探索与实践[J]．数学教育学报，2016，25（4）：30-32．

[23] 卢建川，廖运章，王华娇．英国数学英才选拔考试MAT综合难度分析[J]．数学教育学报，2015，24（6）：31-33．

[24] 汪晓勤，洪燕君．20世纪初美国数学教科书中的几何应用——以建筑为例[J]．数学教育学报，2016，25（2）：11-14．

[25] 范良火，吴立建．国际数学教材研究和发展趋势述评和分析——从首届国际数学教材研究和发展会议及其大会报告说起[J]．数学教育学报，2015，24（3）：1-5．

[26] 廖运章，王华娇．英国数学英才选拔考试MAT命题技术分析[J]．数学教育学报，2016，25（3）：34-37．

[27] 高凤萍．PISA数学素养测试对中国基础数学教育的启示[J]．数学教育学报，2015，24（5）：63-66．

[28] 黄鹏展．教学与科研相结合原则在偏微分方程数值解教学中的实践[J]．数学教育学报，2015，24（4）：48-50．

[责任编校：周学智]

Comparative Study on Advanced Mathematics Textbook’ Content between China and America——Taking America Pennsylvania Ninth Edition Textbook and China Tongji Seventh Edition Textbook as Examples

TIAN Shi-qin1, 2, WANG Yu-wen1

(1. Faculty of Education, Harbin Normal University, Heilongjiang Harbin 150025, China;2. School of Mathematics and Statistics, Changshu Institute of Technology, Jiangsu Changshu 215500, China)

Adopting the combination of qualitative and quantitative research methods, this article compared China advanced mathematics textbook with America. The study found that: there was a greater difference of the content system arrangement and difficulty between the two version textbooks. Tongji seventh edition paid attention to the system of mathematics knowledge and the rigor of mathematics theories, and the exercises focused on pure mathematics problem; Pennsylvania ninth edition paid attention to the mathematical intuition, realistic application and study guiding, and the exercises focused on the practical problems with real data source. Tongji seventh edition was higher than Pennsylvania ninth edition on the whole difficulty. The number of Tongji seventh edition’s knowledge point was 1.3 times of Pennsylvania ninth edition in the common content. The contents depth and problems’ difficulty of Tongji seventh edition was higher than Pennsylvania ninth edition in the knowledge groups of “basic knowledge”, “differential”, and “integral”. Based on the above analysis, it was suggested that we should pay attention to the embodiment of the advanced mathematics application value in different subjects, increase intuitive present appropriately, paid attention to the generation process of mathematics knowledge, and the learning guidance when compiling advanced mathematics teaching textbook.

advanced mathematics; textbook; content; difficulty; comparison

G642

A

1004–9894（2017）02–0075–05

2017–02–10

天津市教育科学规划（一般）项目——智慧教育背景下智慧型教师培养策略研究（HE3064）

田仕芹（1977—），女，山东日照人，哈尔滨师范大学博士生，常熟理工学院讲师，主要从事数学教学与数学教育评价研究．