初中生数学学习兴趣问卷编制与现状调查

吴洪艳，刘晓琳



初中生数学学习兴趣问卷编制与现状调查

吴洪艳1，刘晓琳2

（1．内江师范学院教育科学学院，四川内江 641100；2．隆昌一中，四川内江 642150）

以国外学习兴趣四阶段理论为指导，自编初中生数学学习兴趣初始问卷．经因素分析确定了激发的情境兴趣、维持的情境兴趣与个体兴趣3因素17题项的正式问卷．运用问卷对588名初中生进行调查，结果发现：（1）中国初中生数学情境兴趣尚可，个体兴趣亟待提高．（2）情境兴趣存在显著的校际、年级与班际差异，个体兴趣只存在班际差异，不存在校际与年级差异．（3）学校教学理念与教学条件，特别是教师，是影响初中生数学学习兴趣最为重要的因素．

初中生；数学学习兴趣；问卷编制；现状调查；原因分析；教育建议

1 引 言

学习兴趣是影响学习的重要变量．国外学者对学习兴趣进行了深入系统的研究，提出了具有很强解释效应与指导意义的学习兴趣产生根源与机制的理论[1~2]，对学习兴趣的内部结构[3~7]及其影响与作用[8~10]进行了大量的实证研究．个体兴趣与情境兴趣的划分是国外学习兴趣结构研究的标志性成果．前者被界定为一种个人长期、深入地与某一主题或领域相联系而产生的个性倾向；后者被被界定为一种由活动或学习任务的特征对个体产生的吸引力激发的即时的、积极的心理状态[7，11~12]．Hidi与Renninger[7]在总结前人以及自己对学习兴趣长期研究的基础上，进一步将情境兴趣划分为激发的情境兴趣与维持的情境兴趣（前者是由短期的情感与认知过程的改变导致的一种兴趣的心理状态，它主要受环境与文本特征的激发；后者是继前者之后的一种兴趣的心理状态，包括能够延续一段时间的集中的注意力与坚持力，它主要是由任务的意义性与个人卷入维持的）、将个体兴趣划分为初现的个体兴趣与成熟的个体兴趣（二者表现为不同程度的肯定的情感、储存的知识与储存的价值），从而提出了西方学习兴趣结构研究的总结性成果——学习兴趣四阶段发展理论．学习兴趣发展的不同阶段具有不同的特点、不同的影响因素与促进措施，因此，了解学生学习兴趣所处阶段与特点对学生学习兴趣的培养具有重要的价值与意义．

数学是学习和研究现代科学技术必不可少的工具，也是中小学最为重要的课程之一．众多研究发现学习兴趣是影响学生数学学习的重要的非智力因素[13~15]，王光明、宋金锦等在编制高中生数学学习非智力特征调查问卷时，将学习兴趣作为推动、指引和维持数学学习的认知性动机编入了问卷[16]；焦彩珍发现初中生数学学习兴趣、数学学业自我效能和数学学业成绩之间存在显著的正相关[17]．初中阶段是学习兴趣形成与发展的重要时期，初中数学较大的抽象性与较强的逻辑性使得初中生数学学习容易发生两极分化现象——如果教师引导得当，学生很容易对数学产生浓厚的学习兴趣，反之，则很容易失去对数学的学习兴趣甚至放弃数学学习，如戴凤鸣、姚林调查发现农村数学学困生存在对数学缺乏学习兴趣的情意特征[18]．因此，深入分析研究初中生数学学习兴趣的特征与影响因素具有特别重要的价值与意义．研究拟以Hidi与Renninger[7]的学习兴趣四阶段理论的建构为指导编制初中生数学学习兴趣问卷，探索中国初中生数学学习兴趣的结构，并运用自编问卷进行调查，以了解当前中国初中生数学学习兴趣的状况，并进一步分析原因，继而提出具有针对性的培养措施．

2 初中生数学学习兴趣问卷编制

2.1 项目的搜集与整理

初始问卷以学习兴趣四阶段理论[7]建构为指导，在广泛查阅相关文献与深入访谈基础上，结合初中生数学学习特点与学习环节编制了69个初始条目．经过反复修订形成一个56个条目、从非常不符合到非常符合1~5级评分的初中生数学学习兴趣预测问卷．56个条目中有13个反向条目，7对对偶检测．反向条目反向计分，各条目得分越高学习兴趣越高．

2.2 项目分析

使用56个条目的预测问卷，对A中学初一到初三每个年级一个好班（学生入学时基础好，一般教师配备也较好）、一个差班（学生入学时基础差，一般教师配备也较差），共计358名初中生进行问卷调查，经对偶检测后保留330名被试，其中初一114人、初二116人、初三100人，女生175人、男生155人．采用SPSS19.0进行项目分析．极端值比较发现高分组（前27%）与低分组（后27%）被试各条目得分差异极其显著（>0.70，<0.001），表明各条目区分度很好；题总相关发现，所有条目得分与学习兴趣总分的相关>0.40，相关非常显著（<0.01），表明各条目与整体量表同质性高．根据各条目信度分析结果，删除修正的条目总相关<0.40以及条目删除后总量表的值大于删除前总量表值的一个条目；根据共同性与因素负荷分析的结果，删除共同性<0.20、因素负荷量<0.45的4个条目．项目分析共删除5个条目，保留51个条目参与探索性因素分析．

2.3 探索性因素分析

采用潜变量建模软件Mplus4.2对项目分析后的51个条目进行探索性因素分析．首先，对330名预测被试取样进行适当性检验，得到KMO值为0.966，Bartlett’s球形检验<0.001，表明数据样本非常适合进行因素分析．偏度与峰度分析发现，所有条目的偏度与峰度系数都<2，因此，采用ML估计是合适的，为了获得更稳健的参数估计结果，采用稳健极大似然估计MLR估计．另外，从理论角度以及前人研究结果[3，6]来看，学习兴趣几个因子之间存在较大的相关，因此，选择斜交旋转法．虽然许多人在因素分析时，将特征值大于1作为抽取因子的依据，但相关研究证实，当变量数超过40时，采用特征值大于1的方法会造成高估因子数目的情况[19]．平行分析结合碎石图被认为是探索性因素分析中因子保留最精确的方法[20]．研究采用平行分析法结合碎石图来决定抽取因子的个数．平行分析发现从模拟的随机数据中抽取的前3个因子的特征值1.861、1.771、1.706小于实际数据中抽取的前3个因子的特征值22.633、2.554、2.057，从模拟的随机数据中抽取的第4个因子的特征值为1.651，大于实际数据中抽取的第4个因子的特征值1.491，从碎石图上也可以看到第3个因子处出现明显的拐点，因此，决定抽取3个因子．依据因子载荷≥0.45，交叉载荷<0.30，以及在非归属因子上载荷<0.25，每个因子条目基本相当的原则保留条目．经过3次旋转，最终形成的问卷含3个因子，共18个条目．3个因子的累计方差贡献率为62.16%．

根据问卷编制时的理论构想与3个因子具体条目内容，将5个条目的因子1命名为激发的情境兴趣（SI1），6个条目的因子2命名为维持的情境兴趣（SI2），7个条目的因子3命名为个体兴趣（II）．3个因子具有理想的中度相关（相关系数在0.50~0.70之间），所有条目在其归属的因子上的载荷都大于0.55（见表1）．

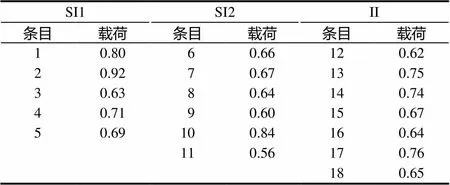
表1 初中生学习兴趣问卷18个条目载荷

2.4 验证性因素分析

运用18个条目的再测问卷对B中学每个初中年级16个班中随机抽取的3个初一班、2个初二班、2个初三班，共计272名初中生进行调查，经对偶检测后保留258人，有效率94.85%，其中初一114人、初二72人、初三72人，男生133人、女生125人．使用再测数据，运用Mplus4.2对3因子18条目的结构模型进行验证，结果发现拟合指数较为理想（见表2 CFA18），为了进一步改善拟合指数，根据Mplus报告的修正指数，删除SI2中与第6题重叠的第7题(y7 with y6 M.I.=43.863)，各项拟合指数有了进一步的改善（见表2 CFA17）．

表2 初中生数学学习兴趣量表验证性因素分析各项拟合指数

2.5 信效度检验

采用内部一致性方法对问卷的信度进行分析．总问卷的Cronbach’s Alpha系数为0.915，3个因子的系数依次为0.854、0.809、0.910，表明初中生数学学习兴趣问卷具有良好的稳定性．

初中生数学学习兴趣预测问卷在前人研究理论的基础上提出问卷维度的初步构想，问卷结构和条目测查方法参考了国内外大量研究文献，在具体条目上，听取了心理学专家以及心理学研究生、初中一线教师的意见以及5名初中生被试当场作答的反馈意见，反复增删、修改而成，因此，该问卷具有良好的内容效度．

3 初中生数学学习兴趣现状调查

初中生数学学习兴趣正式问卷共17个条目，各条目均采用5点计分（1=非常不符合，5=非常符合），反向条目反向计分，得分越高学习兴趣越高．学习兴趣水平根据各分量表平均分，分为无兴趣（≤<2）、兴趣不稳定（2≤<3）、感兴趣（3≤<4）、很感兴趣（4≤≤5）4种水平（为条目数）．采用“初中生数学学习兴趣问卷”对588名初中生进行问卷调查，运用SPSS19.0进行统计检验．588名被试330名来自A中学、258名来自B中学．A中学是市属公办完全中学，代表一般初中；B中学是一所纯初中学校，地处中国科技城——四川省绵阳市腹心地带，是绵阳市涪城名校，国家基础教育实验中心外语实验学校、国家教育部人文社科项目实验学校，代表较好的初中．拟通过具有代表性的两所学校学生数学学习兴趣的比较，较为全面地了解初中生数学学习兴趣现状．

3.1 初中生数学学习兴趣水平

从表3可见，从3个分量表与总量表平均分来看，588名初中生SI1、SI2与LI都处于感兴趣水平，II处于兴趣不稳定水平．将感兴趣与很感兴趣人数百分比相加发现，具有SI1、SI2与II的学生人数百分比依次为：84.35%、76.53%、46.43%．以正态分布曲线下各学习兴趣水平（各占1.5个标准差）人数为理论数据，进行频数分布正态性的检验，结果发现，SI1、SI2呈正偏态分布，II呈负偏态分布，且相较于正态分布，无II的学生比例很高、具有II的学生比例很低．

3.2 初中生数学学习兴趣的校际差异

从表4可见，B中学初中生SI1、SI2与LI显著高于A中学，但II差异不显著．

3.3 初中生数学学习兴趣年级差异

从表5可见，588名初中生SI1与SI2存在显著的年级组间差异，II组间差异不显著．从表6可见，两所学校分别进行的年级间差异比较发现：A中学学生在3个分量表上都存在非常显著的年级组间差异，事后两两比较发现初二年级在3个分量表上都显著低于一三年级，而一三年级只有SI1存在显著差异；B中学的3个分量表都不存在年级组间差异，事后两两比较发现只有初三年级SI2显著低于一二年级．

表3 588名初中生数学学习兴趣平均数和标准差及各水平人数/百分比与正态分布检验

注：SI1、SI2、II、LI题目数即依次为5、5、7、17；卡方检验时=3，(0.05)=7.81，(0.01)=11.34；*<0.05，**<0.01，后同

表4 初中生数学学习兴趣校际差异

注：A中学330人，B中学258人，后同

表5 588名初中生数学学习兴趣年级差异

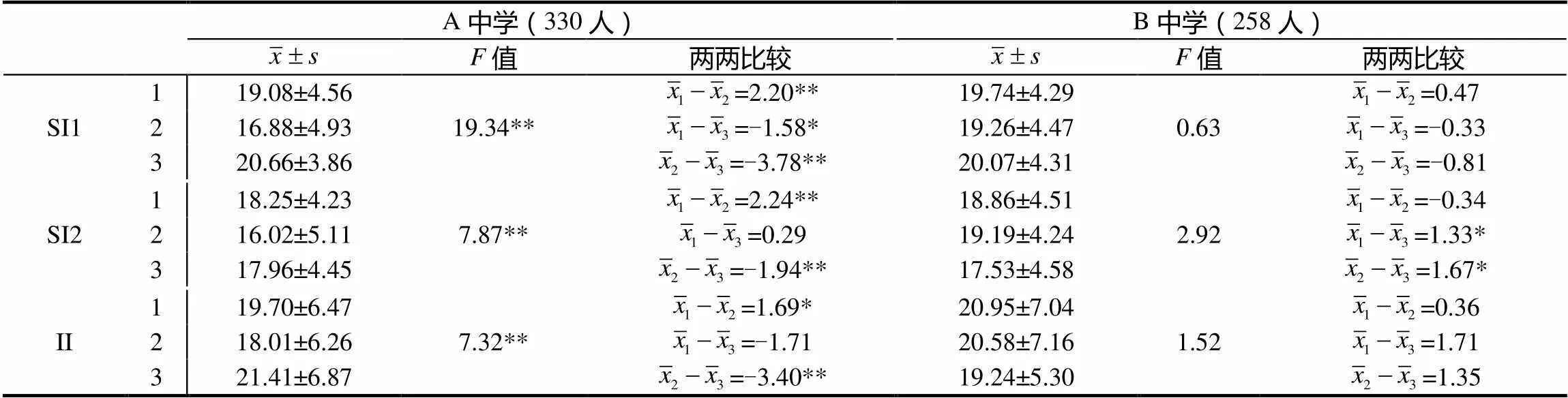
表6 A中学330名被试与B中学258名被试数学学习兴趣年级差异

注：A中学初一114人，初二116人，初三100人；B中学初一114人，初二72人，初三72人

3.4 初中生数学学习兴趣班际差异

方差分析发现，两所学校学生3个分量表都存在显著的班际组间差异，进一步进行同一学校同一年级平行班差异的两两比较发现，B中学同一教师任教的两个初一班3个分量表不存在任何差异，A中学同一教师任教的两个初三班只有SI2上存在差异．

4 讨 论

4.1 初中生数学学习兴趣问卷的编制

研究验证了Hidi和Renninger学习兴趣四阶段理论的跨文化适应性，同时体现出了中国特色．即该研究得到的学习兴趣的一阶3因子模型既反应了情境兴趣与个体兴趣的区别，也反应了情境兴趣的两个阶段——激发的情境兴趣与维持的情境兴趣，同时，相较于Mitchell[3]的二层次模型更为简洁、更好把握，也更符合中国人的思维与认识，即学习兴趣始于激发的情境兴趣，最后发展为个体兴趣，维持的情境兴趣是二者的桥梁与中介．3因子模型也证实了初现的个体兴趣与成熟的个体兴趣只是量上的差异而无质上差异的猜测，二者应该可以通过个体兴趣分量表上分值的高低予以区分，具体区分的分数界限还有待在后续研究中探索确定．

研究依据已有的学习兴趣结构理论，在广泛查阅资料与访谈基础上编制问卷条目，并对问卷条目进行反复考查和修订，形成预试问卷，因而，问卷具有良好的内容效度．验证性因子分析发现，探索性因素结构模型的拟合指数良好，各因子具有理想的中度相关，表明问卷具有较好的结构效度．信度检验结果显示，问卷具有良好的内部一致性信度．可见，该研究所编制的初中生数学学习兴趣问卷结构清晰、简单明了，具有理想的效度与信度以及较强的鉴别与诊断能力．

4.2 初中生数学学习兴趣现状

4.2.1 初中生数学情境兴趣尚可

研究发现，中国初中生数学SI1与SI2各水平人数呈正偏态分布，分别有84.35%与76.53%的学生具有SI1与SI2．这表明，当前中国初中生数学情境兴趣尚可．但是，情境兴趣是短暂的、表浅的，是外部激发与外部维持的，稳定持久、内部激发、自我发动的个体兴趣才是学习兴趣培养的最终目的所在．该研究调查的两所学校学生的SI1与SI2均分都还仅处于感兴趣水平，根据Hidi与Renninger（2006）[7]的观点，只有持久浓厚的前一阶段的学习兴趣才可能向后一阶段发展，因此，中国初中数学课堂教学还需进一步提高学生的SI1与SI2．

4.2.2 初中生数学个体兴趣亟待提高

研究发现初中生数学II均分处于兴趣不稳定水平，各水平学生人数呈负偏态分布，只有46.43%的学生具有II，而且这种低下的II只存在一定的班际差异而不存在校际差异，也不存在初三年级与初一年级的差异．这表明中国初中生数学II普遍低下，更为糟糕的是初中三年对学生II的培养没有起到任何促进作用．

乌克兰教育家苏霍姆林斯基说：“如果一个学生到十二三岁时还没有兴趣爱好，做老师的要为他担忧，担心他长大以后对任何事情漠不关心，成为一个平平庸庸的人．”初中阶段是学生学习兴趣基本形成的阶段，如果一个学生在初中阶段还没有形成学习兴趣，则其以后的发展就会受到很大的影响．因此，中国初中生数学个体兴趣亟待提高．

4.3 初中生数学学习兴趣影响因素的分析

4.3.1 学校教学条件与教育理念影响初中生数学学习兴趣

研究发现，B中学初中生数学情境兴趣（包括SI1与SI2）显著高于A中学．B中学是一所办学条件较好、办学理念较为先进的纯初中，青年教师较多，教师在课堂教学中更多地采用了多媒体教学与小组合作的教学方式，师生互动、生生互动较多；另外，相比于A中学，B中学班级规模更小（一个班学生45人左右，而A中学则在60人以上），更有利于教师一对一的辅导．因此，B中学学生数学情境兴趣更高．

研究还发现，A中学初二年级学生在各个分量表上得分都最低，这符合人们所说的“初二现象”．即初二学生处于身心巨变、心理断乳最危险的时期，逆反心理最重、最难管理，最容易出现早恋、上网、成绩下滑等问题，容易对学习失去兴趣．但这种现象在B中学并不存在，这说明，“初二现象”可能存在，但是远不如人们所说的那么严重，或者说这种“初二现象”通过合理的教育是可以避免的．

4.3.2 教师素质是影响初中生数学学习兴趣最为重要的因素

研究发现，初中生数学学习兴趣存在显著的班际差异，但是B中学同一教师任教的两个初一班不存在任何差异，A中学同一老师任教的两个初三班差异甚微，出现入学时数学基础更差的班SI2显著高于基础更好的班、II达到感兴趣水平（3*7≤22.00<4*7）的反常现象（其他年级均是好班学习兴趣高于差班，II处于兴趣不稳定水平）．A中学同时任教初三两个班的老师是公认的好老师，这两个班的SI1都达到了很感兴趣水平（4*5≤20.66<5*5），II总均分达到了感兴趣水平（3*7≤21.41<4*7）．可见，教师才是学生学习兴趣最重要的影响因素．史炳星从多年数学教师的经验出发，认为相当一部分孩子从喜欢数学到不喜欢数学，很大成分归结为数学教育观念、教学方法和评估方法不重视、爱护和培养学生的学习兴趣，不能经常让学生自己动手学习和尽可能地使数学联系实际[21]．

5 结 论

（1）初中生数学学习兴趣问卷的结构由激发的情境兴趣、维持的情境兴趣与个体兴趣3个因子构成；初中生数学学习兴趣问卷具有良好的信效度，且3因素结构模型具有良好的拟合度，说明初中生数学学习兴趣问卷适合作为初中生数学学习兴趣的测量工具．

（2）中国初中生数学情境兴趣有待进一步提高，个体兴趣亟需提高．

（3）学校教学理念与教学条件，特别是教师，是影响初中生数学学习兴趣最为重要的因素．

[1] Andreas Krapp. Basic Needs and the Development of Interest and Intrinsic Motivational Orientations [J]., 2005, 15(5): 381-395.

[2] Edward L Deci, Richard M Ryan. The “What” and “Why” of Goal pursuits: Human Needs and the Self-Determination of Behavior [J]., 2000, 11(4): 227-268.

[3] Mitchell Matthew. Situational Interest: Its Multifaceted Structure in the Secondary School Mathematics Classroom [J]., 1993, 85(3): 424-436.

[4] Deci E L. The Relation of Interest to the Motivation of Behavior: A Self-Determination Theory Perspective [A]. In: Renninger K A, Hidi S, Krapp A.[C]. Hillsdale, NJ: Lawrence Erlbaum Associates, Inc., 1992.

[5] Chen A, Darst P W, Pangrazi R P. What Constitutes Situational Interest? Validating a Construct in Physical Education [J]., 1999, 3(3): 157-180.

[6] Lisa L G, Amanda M D, Anne M C, et al. Measuring Situational Interest in Academic domains [J]., 2010, 70(4): 1-25.

[7] Hidi S, Renninger K A. The Four-Phase Model of Interest Development [J]., 2006, 41(2): 111-127.

[8] Renninger K A, Wozniak R H. Effect of Interest on Attention Shift, Recognition, and Recall in Young Children [J]., 1985, 21(4): 624-632.

[9] Renninger K A, Ewen L, Lasher A K. Individual Interest as Context in Expository Text and Mathematical Word Problems [J]., 2002, 12(4): 467-491.

[10]  Harackiewicz J M, Barron K E, Tauer J M, et al. Predicting Success in College: A Longitudinal Study of Achievement Goals and Ability Measures as Predictors of Interest and Performance from Freshman Year Through Graduation [J]., 2002, 94(3): 562-575.

[11]  Hidi S, Baird W. Strategies for Increasing Text-Based Interest and Students’ Recall of Expository Texts [J]., 1998, 23(4): 465-483.

[12]  Hidi S. Interest and Its Contribution as a Mental Resource for Learning [J]., 1990，60(4): 549-571.

[13] 房之华．以非智力因素促进学生智力和能力的发展[J]．数学教育学报，1999，8（3）：34-37．

[14] 颜中玉．非智力因素对高师数学学习影响的调查[J]．数学教育学报，2001，10（2）：44-47．

[15] 李如．非智力因素对高职类文科生高等数学学习效果的影响[J]．数学教育学报，2006，15（4）：76-78．

[16] 王光明，宋金锦，王兆云．高中生数学学习非智力特征调查问卷的编制[J]．数学教育学报，2015，24（3）：17-27．

[17] 焦彩珍．初中生数学学习兴趣及自我效能与数学学业成绩的关系[J]．数学教育学报，2008，17（2）：44-46．

[18] 戴风明，姚林．农村初中数学学困生情意特征的调查研究[J]．数学教育学报，2001，10（4）：96-99．

[19] 吴明隆．问卷统计分析实务——SPSS操作与应用[M]．重庆：重庆大学出版社，2010．

[20] 王孟成．潜变量建模与Mplus应用（基础篇）[M]．重庆：重庆大学出版社，2014．

[21] 史炳星．谈对学生数学学习兴趣的爱护和培养[J]．数学教育学报，1999，8（2）：94-97．

附录：初中生数学学习兴趣正式问卷

初中生数学学习兴趣问卷

(Junior High School Students’ Mathematics Learning Interest Questionnaire, JHSSMLIQ)

因子项目 激发的情境兴趣1. 数学老师有趣． 2. 数学课堂气氛轻松愉快． 3. 数学课有趣． 4. 数学课堂气氛单调沉闷． 5. 数学课堂气氛和谐融洽． 维持的情境兴趣6. 数学课上，我容易走神． 7. 我学习数学需要别人的督促． 8. 碰到数学难题我会放弃． 9. 我对数学公式与定理不熟悉． 10. 我学习数学就是为了考试． 个体兴趣11. 我喜欢探究数学公式与原理的来龙去脉． 12. 我喜欢不断尝试新的、更有效的学习与研究数学的方法与策略． 13. 如果有数学竞赛活动，我会主动报名参加． 14. 谈起数学的相关知识，我才思如泉涌，口若悬河、滔滔不绝． 15. 伟大的数学家是我奋斗的榜样． 16. 我喜欢做数学难题． 17. 我以后想从事与数学相关的职业．

[责任编校：周学智]

Development of Mathematics Learning Interest Questionnaire and the Investigation on Junior High School Students

WU Hong-Yan1, LIU Xiao-lin2

(1. School of Education, Neijiang Normal University, Sichuan Neijiang 641100, China;2. Longchang No.1 Middle School, Sichuan Neijiang 642150, China)

Based on the four-phase model of learning interest, we developed a mathematics learning interest questionnaire on junior high school students. Including 17 items and three factors called triggered situational interest (SI1), maintained situational interest (SI2) and individual interest (II) We put it into use and found that: (1) The SI1 and SI2 are acceptable；The II is inferior. (2) There’s significant difference in schools, grades and classes of SI1 and SI2. And there is no significant difference in schools and grades of II. (3) School teaching philosophy and teaching conditions, especially teachers, are the most important reasons for the junior middle school students’ interest in mathematics learning.

junior high school students; mathematics learning interest; the development of questionnaire; survey; cause analysis；education suggestions

G632.0

A

1004–9894（2017）02–0050–05

2016–12–18

吴洪艳（1973—），女，贵州雷山人，副教授，硕士，主要从事教育与心理应用研究．