采用结构保护策略的强制进化随机游走算法优化换热网络
2017-10-13鲍中凯崔国民陈家星
鲍中凯,崔国民,陈家星
采用结构保护策略的强制进化随机游走算法优化换热网络
鲍中凯,崔国民,陈家星
(上海理工大学新能源科学与工程研究所,上海200093)
鉴于强制进化随机游走算法(random walk algorithm with compulsive evolution, RWCE)在优化换热网络时可能出现有潜力结构被差解代替,提出了一种结构保护策略,增加一个与原种群平行进化的新种群,新种群执行结构保护,个体与原种群一一对应并接收其当前最优解,同时采用一种降维邻域搜索的进化方式,设置个体各维变量更新概率确定搜索维数,充分挖掘个体结构进化潜力,提升了算法的局部搜索能力;原种群则沿用RWCE的主要操作,保留了较强的全局搜索能力。将采用结构保护策略的RWCE算法用于有分流换热网络优化,取得了优于现有文献的结果。
强制进化随机游走算法;结构保护策略;换热网络;优化
引 言
换热网络综合是过程系统中的一个重要领域,深受国内外学者的重视[1]。作为工程领域优化换热网络的重要方法,夹点法[2]分别以最小公用工程耗量和最小换热单元数为目标分步求解换热网络问题,这类基于分步思想的优化方法[3-5]割裂了公用工程耗费、固定投资费用和面积费用之间的关系,无法得到全局最优解[6]。因此,换热网络的同步优化模型被提出[7],该模型的优化方法包括确定性方法和启发式方法[8]。
基于混合整数非线性(mixed-integer nonlinear programming, MINLP)数学模型的换热网络同步优化问题具有极强的非凸、非线性,被证明是NP-难问题[9]。确定性方法在处理这类问题时存在效率较低、易陷入局部极值的不足,而启发式方法具有灵活、高效且不依赖问题本身的优点,能够取得较好的结果[10-12]。启发式方法如遗传算法(genetic algorithm, GA)[13]、微分进化算法(differential evolution, DE)[14]、禁忌算法(tabu search, TS)[15]及粒子群算法(particle swarm optimization, PSO)[16]等已经得到广泛的应用。陈帅等[17]提出了一种自适应调节速度权重的PSO算法,提升了算法效率和局部收敛精度;Yu等[18]提出了一种GA和模拟退火(simulated annealing, SA)的混合算法,可有效解决大规模换热网络问题;Huo等[19]提出了一种双层算法,将GA用于上层网络结构的优化,改进的PSO用于下层换热量、分支流量等连续变量的优化;Pavão等[20]基于简化的SA和PSO同样采用了双层优化策略。这些方法具有一定跳出局部最优的能力,但依然会出现种群多样性丧失而导致早熟收敛。强制进化随机游走算法(random walk algorithm with compulsive evolution, RWCE)是一种新的启发式方法,该算法被用于换热网络优化,取得了较好的结果[21-22]。RWCE采用个体独立“游走”的方式,通过各方向简单的随机游走和设置最小换热量实现了换热网络连续变量和整型变量的同步优化,保证了算法的种群多样性,提升了全局搜索能力。
以一定概率接受差解有助于跳出局部极小值,是RWCE进行全局搜索的一个重要支撑,但容易出现差解代替具有进化潜力的解,造成局部搜索不充分。本文提出了采用结构保护策略的RWCE(random walk algorithm with compulsive evolution with structure-protection strategy, SP-RWCE),保持全局搜索能力的同时充分挖掘所保护结构的进化潜力,增强算法局部搜索能力。
1 换热网络数学模型
1.1 问题描述
采用Björk等[23]使用的基于非等温混合假设的换热网络分级超结构模型,如图1所示。热流体股数为H,冷流体股数为C,记匹配编号=1,2,…,,是最大匹配数H×C×S。每级内每股热流最多可分C个分支,每股冷流最多可分H个分支。
1.2 目标函数
优化的目标为最小年综合费用(total annual cost, TAC),表达式为
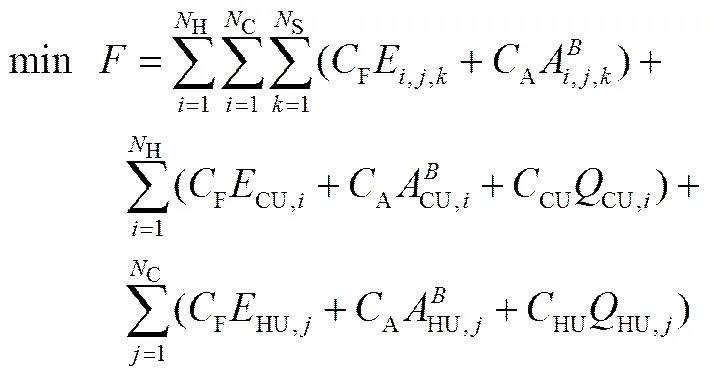
其中,是待优化的整型变量,表示换热器是否存在(存在时取1否则取0)。面积计算公式为
(2)
1.3 主要约束
(1)流股总热平衡

(4)
(2)流股级内热平衡

(6)
(3)单个换热器热平衡

(8)
其中,h,j,k和c,j,k分别为热、冷流股的分流比。分流比表示分流热容流率占该流股总热容流率的比例。
(4)非等温混合能量平衡

(10)
(5)分流质量平衡
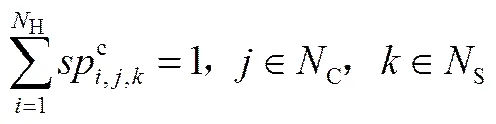
(12)
(6)公用工程热平衡

(14)
此外,换热器冷、热端的最小换热温差为Dmin。
2 RWCE算法主要操作
RWCE 主要操作包括初始化、个体游走、个体选择和个体变异。首先在可行域按照式(15)均匀初始化个个体,每个个体代表问题的一个解。
G,p,0=max×(0,1) (15)
其中,G,p,0代表个体第维变量初始值,=1,2,…,,=1,2,…,,为变量总维数,max为变量初始最大值。
随后对个体按照式(16)进行各维变量的随机游走实现个体更新。

其中,G,p,it、′,p,it+1分别为个体第次迭代的第维变量初始值和该维游走后的变量值,max是最大进化步长。设置变量下界min同步优化整型变量[式(17)],即当′,p,it+1小于min时对应整型变量为0,否则为1,最终得到变量有效值″,p,it+1。
(17)
比较个体进化后有效解″,it+1[式(18)]对应适应度函数(″,it+1)和进化前初始解,it对应(,it),函数值低的解被选为下一次迭代的初始解,it+1,实现“个体选择”;若(″,it+1)未能低于(,it),则执行“个体变异”,以一定概率接受差解,具体操作如式(19)所示。若满足终止条件,迭代结束,否则继续执行式(16)~式(19)。此外,(0,1)、、和均为(0,1)内均匀分布的随机数。

(19)
RWCE在优化无分流换热网络时取得了较好的效果[21-22],本文将其嵌入到有分流数学模型中,G,p,it可具体表示为换热量和热、冷流股分流比等3组待优化的连续变量。通过设置换热量下界min,按式(17)决定换热单元的生成和消去即能实现整型变量的优化,因此整型变量优化包含在换热量的优化中。分别记换热量和热、冷流股分流比的初始最大值为max和max、max,引入换热量最大进化步长q,max、热流股分流比最大步长h,max和冷流股分流比最大步长c,max。其中本文h,max、c,max由对应分流上的换热量决定:换热量为0时,h,max=c,max=0.2,否则h,max=c,max=0.1。
3 SP-RWCE算法优化换热网络
在全局优化进程中,每个个体的当前最优解都是具有进化潜力的好结构。如果沿用RWCE的进化方法,个体最优解难以得到进一步优化,且容易被差解代替。因此,SP-RWCE在RWCE原种群的基础上增加一个新种群,新种群个体接收原种群对应个体的当前最优解形成保护,并采用一种新的进化方式,通过限制执行随机游走的变量维数,充分挖掘个体进化潜力;同时原种群继承了RWCE较强的全局搜索能力。以下将结合实例分析结构保护策略的合理性和有效性,并给出SP-RWCE的算法流程,最后对其求解效率进行分析。
3.1 结构保护策略
RWCE以一定概率接受差解容易造成有进化潜力的解被差解代替,导致局部搜索不充分。为了更好地说明这种情况,以9股流算例为例,算例参数如表1所示。采用RWCE得到了TAC为2932215 USD·a-1的网络结构(图2,括号内为分流比),参数如下:=36,max=200 kW,q,max=100 kW,max=max=10,min=90 kW,=0.01,S=4。

表1 9股流算例参数
Note: Annual cost of heat exchangers=2000+70USD·a-1(in m2); annual cost of hot utility=60 USD·kW-1·a-1; annual cost of cold utility=6 USD·kW-1·a-1.
以图2中的结构作为初始解,参数不变,跟踪一个个体观察RWCE优化过程中该个体最优TAC和每次迭代被选择TAC的变化情况,迭代曲线如图3所示,个体累计接受差解次数如表2所示。

表2 个体累计接受差解次数
可以发现不断接受差解后,个体结构难以回到当前最优,甚至会往更差方向随机游走,导致算法陷入停滞。针对这一缺陷,如果采用“不接受差解”的处理方式,那么容易使个体过早陷入局部陷阱而无法跳出,导致进化的停滞;如果由个体自识别优化进程从而决定是否接受差解,这又很难实现,因为换热网络属于复杂的MINLP问题,无法得知个体所处的空间环境[24]。
因此,为了保护结构进化潜力,本文提出针对个体当前最优解的结构保护策略,设置一个与原种群(基本层)平行进化的新种群(保护层),保护层个体与基本层一一对应并接收其当前最优解,既可保持基本种群的正常进化和全局搜索能力,又利于有潜力结构的进一步优化。
3.1.1 基本层进化 基本层进化沿用RWCE的主要操作,只在“个体选择”阶段添加如式(20)所示的结构传递操作。如果基本层个体的有效解″1,n,it+1对应年综合费用(″1,n,it+1)低于当前最低费用1,n, min,则传递给保护层相应的第个个体作为其本次迭代的初始解2,n,it。
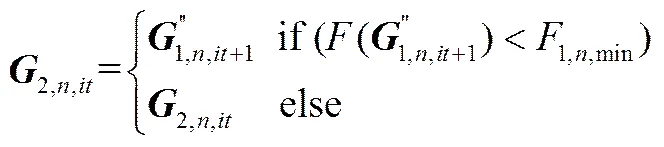
3.1.2 保护层进化 保护层采用一种降维邻域搜索的进化方式。在“个体游走”阶段,保护层个体各维变量是否随机游走取决于变量更新概率和(0, 1)内均匀分布的随机数,具体操作如式(21)所示,当=1时,式(21)同式(16)。
(21)
采用式(21)的进化方式,以图2结构为初始解,分别取=1和=0.04,图4为取不同值时年综合费用迭代变化曲线(均取0)。从图中看出,当=0.04时,TAC下降很快且最终为2925119 USD·a-1;而=1时,最终得到的TAC为2930924 USD·a-1,虽然比图2降低1291 USD·a-1,但是比=0.04时多出5805 USD·a-1,且下降过程缓慢。
取=1即执行个体各维变量的随机游走,这种进化方式具有较强的全局搜索能力,特别是进化前期以一定的概率接受差解使得年综合费用下降很快。但在进化后期,个体接近全局最优解时,部分变量已经处于最优,此时只有实现几个变量的联合增减才能保证年综合费用下降。因此,取=0.04即采用降维邻域搜索的进化方式,只搜索个体的部分维度,有利于连续变量优化即更加合理分配换热量和分流比,充分挖掘结构的进化潜力。
3.2 SP-RWCE算法流程
SP-RWCE算法流程如图5所示,其关键步骤如下。
(1)初始化:设置两个规模相同的种群,按式(15)对换热量和分流比进行初始赋值。
(2)个体游走:基本层和保护层个体分别按式(16)和式(21)执行随机游走;设置两种群的最小换热量为1,min和2,min,按式(17)处理整型变量。
(3)个体选择:若个体游走后年综合费用更低则被选为下次迭代初始解,基本层个体最优解每更新一次,对应执行一次式(20)的最优解传递操作。
(4)个体变异:若个体游走后年综合费用更高,则以一定概率接受该结构,其中保护层2取0,保护当前结构;具体操作如式(19)所示。
(5)终止条件:最优年综合费用连续cr次不变时,终止优化,本文cr取500万次。
3.3 算法效率分析
SP-RWCE的种群规模是RWCE的两倍,表面上计算时间有所增加,但保护层个体接收基本层个体当前最优解并且采用了有效的结构潜力挖掘进化方式,因此SP-RWCE的搜索能力比RWCE提升不止1倍,所以在可接受时间范围内SP-RWCE能够得到更优解甚至获得更优解的搜索效率反升不降。
仍以3.1节的9股流算例为例说明SP-RWCE算法的搜索能力。计算机配置为:CPU Intel(R) Xeon(R) E5-2670,主频2.5 GHz,64GB RAM。图6是用SP-RWCE和RWCE优化时的TAC随时间的变化曲线,极短时间后(25 min)SP-RWCE得到的解已经优于RWCE,而纵观全局,SP-RWCE在较短时间后(50 min)就超越了RWCE得到的最优解,验证了SP-RWCE具有更高的搜索精度和效率。其中RWCE的参数同3.1节,SP-RWCE的基本层参数同RWCE,保护层取=0.04,2,min=10 kW,2=0,其他参数同基本层。
4 实例分析
将SP-RWCE算法应用于非等温混合假设的换热网络分级超结构模型,选取了两个文献中常见的算例,验证了SP-RWCE具有较强的搜索能力。
4.1 算例1
3.3节已经采用RWCE和SP-RWCE对算例1进行了优化,TAC分别为2932215 USD·a-1(图2)和2923840 USD·a-1(图7),与文献结果对比如表3所示。其中文献[28]得到了2905000 USD·a-1的最低TAC,但该文献对换热网络分级超结构模型进行了一些处理,允许单股流体分流存在多个换热器。文献[30]考虑了所有可能的网络结构,得到了2925600 USD·a-1的TAC。当采用一种简化模型时,得到了2922600 USD·a-1的TAC,低于简化模型前的优化结果和本文所得结果。原因是采用简化模型时,缩小了求解域,易于实现算法的充分搜索,但对模型的简化也存在错失更优结果的可能。
SP-RWCE的最优个体来自保护层,图8是该个体与对应基本层个体的TAC迭代曲线。从图8可以看出,两个个体的TAC变化趋势基本一致,当保护层个体接收到基本层个体最优解后,能够充分挖掘其进化潜力,而基本层个体以一定概率接受差解,当前结构易被差解代替,即使未被代替,也难以在各维变量游走的进化方式下得到进一步优化,因此无法获得更优解。可见保护最优解和采用降维邻域搜索的进化方式,提升了算法搜索能力。但从另一角度,若缺少基本层个体,保护层个体也无法得到图7结构,所以保护层是算法得到更优解的关键,基本层的进化是算法主体。

表3 算例1结果对比
4.2 算例2
算例2取自文献[20],具体参数见表4。Pavão等[20]采用了双层优化策略,获得无分流结果为7301437 USD·a-1;Khorasany等[10]同样采用双层算法,上层由和声搜索(harmony search, HS)算法产生结构,下层由混合HS算法和序列二次规划优化换热量和分流比,得到TAC为7435740 USD·a-1。
采用RWCE并设置参数:=36,max=500 kW,q,max=90 kW,max=max=10,min=81 kW,=0.01,S=5,得到图9网络结构,TAC为6983887 USD·a-1。采用SP-RWCE,设置基本层参数同RWCE,保护层取=0.02,2,min= 5 kW,2=0,其他同基本层,得到了图10的网络结构,TAC为6848726 USD·a-1,较之RWCE的优化结果下降了135161 USD·a-1,较之文献[20]下降了452711 USD·a-1。其中最优个体来自保护层,保护层个体平均每次迭代随机游走的变量维数只占总数的2%,通过低维数的邻域搜索充分挖掘出了结构进化潜力。
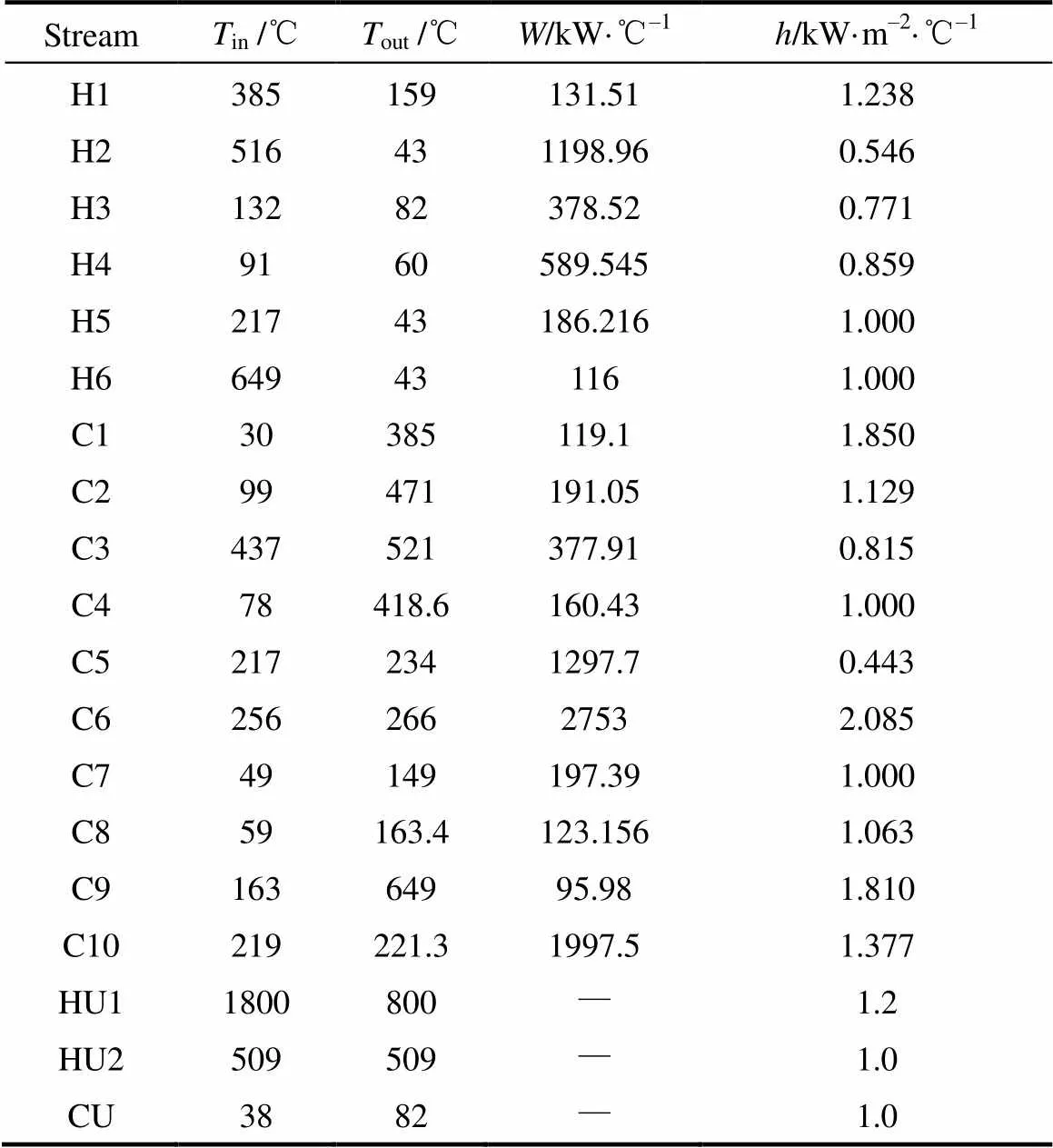
表4 算例2参数
Note: Annual cost of heat exchangers=26600+4147.50.6USD·a-1(in m2); annual cost of hot utility 1=35.0 USD·kW-1·a-1; annual cost of hot utility 2=27.0 USD·kW-1·a-1; annual cost of cold utility=2.1 USD·kW-1·a-1.
当=0.05时,得到的TAC为6889669 USD·a-1(图11)且高于=0.02时的结果,因为对于同一结构,只有保证几个变量联合实现增减,才能使换热量和分流比得到更合理的分配,使结构进化潜力得到充分释放。
因此,为了保证求解质量,本文设置以使1<NHCS<8;并且通过实验和文献得知每个算例较好的结果中存在换热器的大致个数,对于个数多的算例使NHCS相对取大,反之取小。该算例中=0.02即NHCS=6时结果最好,=0.005即NHCS=1.5时结果较好。
结果和文献对比如表5 所示,可见本文结果更优。观察本文得到的结构,发现都只有H2产生了分流,并且其匹配多次,分走了冷流股较多的换热潜能;此外,H3、H4 和H5 流股都没有与冷流股匹配,而是直接使用公用工程进行冷却,因此关于这3条流股的匹配以及连续变量的分布应能得到进一步优化。
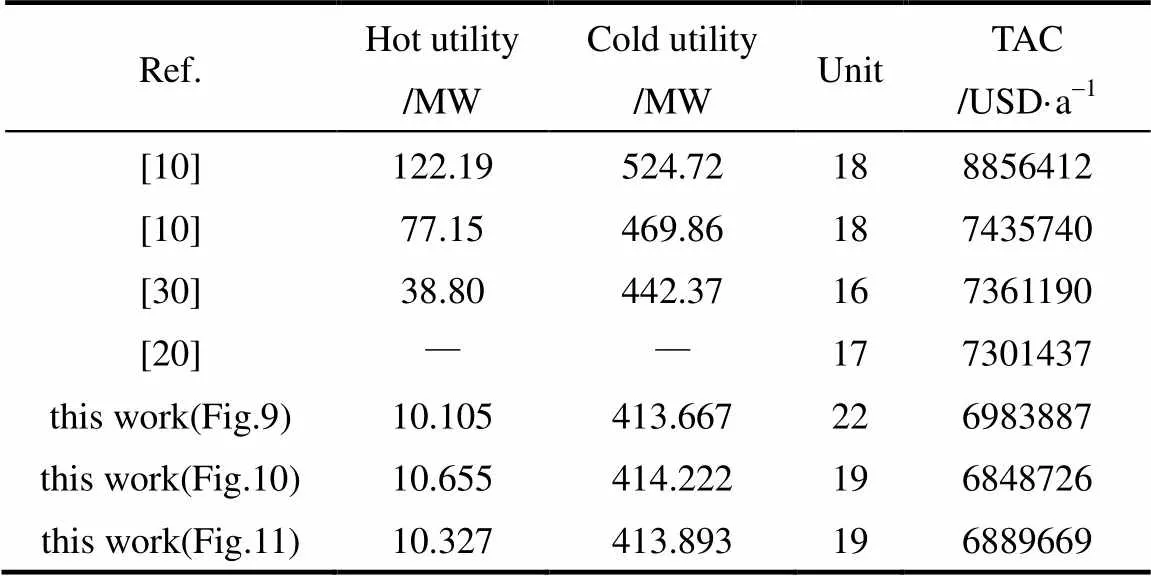
表5 算例2结果对比
5 结 论
(1)本文提出了SP-RWCE算法,设置基本层和保护层两个种群。基本层进化方式同原RWCE,保留了较强的全局搜索能力,是算法的主体部分;保护层执行结构保护,增强了算法的局部搜索能力,是获得更优解的关键。
(2)将SP-RWCE算法应用于有分流换热网络优化,采用两个算例验证了SP-RWCE算法比RWCE具有更强的搜索能力,且优化结果优于多数现有文献。
(3)SP-RWCE保护层个体保护基本层个体当前最优解,并采用降维邻域搜索的进化方式。该进化方式相比RWCE各维变量游走的进化方式,能更加充分且快速地挖掘出结构进化潜力。本文设置使NHCS在区间(1, 8)内,经证明能得到较好的结果。
符 号 说 明

A——换热器面积,m2 B——面积费用指数 CA——面积费用系数 CCU——冷公用工程单位能耗费用 CF——换热器固定投资 CHU——热公用工程单位能耗费用 E——整型变量(取0或1) Gmax——变量初始最大值 Gmin——变量下界 Gn,p,it——个体n第it次迭代的第p维变量初始值 G′n,p,it——个体第p维随机游走后的变量值 G″n,p,it——个体n第p维随机游走后的变量有效值 Gn,it——个体n第it次迭代初始解 G″n,it+1——个体n随机游走后有效解 G2,n,p,it——保护层个体n第it次迭代第p维变量初始值 G′2,n,p,it+1——保护层个体n第p维随机游走后的变量值 itcr——年综合费用连续不变的迭代次数 LMTD——对数平均温差,℃ N——种群规模 NH,NC——分别为热、冷流体股数 NS——级数 QCU,i——热流股i和冷公用工程的换热量,kW QHU,j——冷流股j和热公用工程的换热量,kW Qi,j,k——换热器换热量,kW Qmax——换热量初始最大值,kW Qmin——最小换热量,kW rand(0,1),a,b,g,l——(0, 1)内均匀分布的随机数 Sh,max, Sc,max——分别为热、冷流股分流比最大步长 Smax——最大进化步长 Sq,max——换热量最大进化步长,kW SPhi,j,k,SPci,j,k——分别为热、冷流股的分流比 SPHmax, SPCmax——分别为热、冷流股分流比的初始最大值 Tin, Tout——分别为流股进口和出口温度,℃ ——分别为换热器热分流和冷分流的进口温度,℃ Thi,k,Tcj,k——分别为热分流的混合温度和冷分流的混合温度,℃ ——分别为热流股i和冷流股j的第k级的进口温度,℃ TAC——年综合费用 DTmin——最小换热温差,℃ d——接受差解概率 g——变量更新概率 上角标 in——进口 out——出口 下角标 CU——冷公用工程 HU——热公用工程 i——热流股编号 j——冷流股编号 k——级数编号 n——种群个体编号 p——流股匹配编号(变量编号)
References
[1] AND K F, SAHINIDIS N V. A critical review and annotated bibliography for heat exchanger network synthesis in the 20th century[J]. Industrial & Engineering Chemistry Research, 2002, 41(10): 2335-2370.
[2] LINNHOFF B, HINDMARSH E. The pinch design method for heat exchanger networks[J]. Chemical Engineering Science, 1983, 38(5): 745-763.
[3] PAPOULIAS S A, GROSSMANN I E. A structural optimization approach in process synthesis(Ι): Utility systems[J]. Computers & Chemical Engineering, 1983, 7(6): 695-706.
[4] FLOUDAS C A, CIRIC A R, GROSSMANN I E. Automatic synthesis of optimum heat exchanger network configurations[J]. AIChE Journal, 1986, 32(2): 276-290.
[5] CERDA J, WESTERBERG A W, MASON D,. Minimum utility usage in heat exchanger network synthesis[J]. Chemical Engineering Science, 1983, 38(3): 373-387.
[6] SHETHNA H K, JEZOWSKI J M, CASTILLO F L. A new methodology for simultaneous optimization of capital and operating cost targets in heat exchanger network design[J]. Applied Thermal Engineering, 2000, 20(15/16): 1577-1587.
[7] YEE T F, GROSSMANN I E. Simultaneous optimization models for heat integration (Ⅱ): Heat exchanger network synthesis [J].Compute.Chem.Eng., 1990, 14(10): 1165-1184.
[8] CHOI S H, MANOUSIOUTHAKIS V. Global optimization methods for chemical process design: deterministic and stochastic approaches[J]. Korean Journal of Chemical Engineering, 2002, 19(2): 227-232.
[9] FURMAN K C, SAHINIDIS N V. Computational complexity of heat exchanger network synthesis[J]. Computers & Chemical Engineering, 2001, 25(9): 1371-1390.
[10] KHORASANY R M, FESANGHARY M. A novel approach for synthesis of cost-optimal heat exchanger networks[J]. Computers & Chemical Engineering, 2009, 33(8): 1363-1370.
[11] LIN M H, TSAI J F, YU C S. A review of deterministic optimization methods in engineering and management[J]. Mathematical Problems in Engineering, 2012, 2012(1024-123X): 183-190.
[12] BJÖRK K M, NORDMAN R. Solving large-scale retrofit heat exchanger network synthesis problems with mathematical optimization methods[J]. Chemical Engineering & Processing, 2005, 44(8): 869-876.
[13] DIPAMA J, TEYSSEDOU A, SORIN M. Synthesis of heat exchanger networks using genetic algorithms[J]. Applied Thermal Engineering, 2008, 28(14/15): 1763-1773.
[14] 方大俊, 崔国民. 微分进化算法应用于换热网络全局最优化[J]. 化工学报, 2013, 64(9): 3285-3290. FANG D J, CUI G M. Global optimization of heat exchanger networks using differential evolution algorithm[J]. CIESC Journal, 2013, 64(9): 3285-3290.
[15] LIN B, MILLER D C. Solving heat exchanger network synthesis problems with Tabu Search[J]. Computers & Chemical Engineering, 2004, 28(8): 1451-1464.
[16] SILVA A P, RAVAGNANI M S, JR E B. Particle swarm optimisation applied in retrofit of heat exchanger networks[J]. Computer Aided Chemical Engineering, 2009, 27(9): 1035-1040.
[17] 陈帅, 罗娜. 基于自适应竞争群优化算法的无分流换热网络综合[J]. 化工学报, 2016, 67(11): 4716-4723. CHEN S, LUO N. Adaptive competitive swarm optimization for heat exchanger networks without split streams[J]. CIESC Journal, 2016, 67(11): 4716-4723.
[18] YU H, FANG H, YAO P,. A combined genetic algorithm/simulated annealing algorithm for large scale system energy integration[J]. Computers & Chemical Engineering, 2000, 24(8): 2023-2035.
[19] HUO Z, ZHAO L, YIN H,. A hybrid optimization strategy for simultaneous synthesis of heat exchanger network[J]. Korean Journal of Chemical Engineering, 2012, 29(10): 1298-1309.
[20] PAVÃO L V, COSTA C B, RAVAGNANI M S. Heat exchanger network synthesis without stream splits using parallelized and simplified simulated annealing and particle swarm optimization[J]. Chemical Engineering Science, 2017, 158: 96-107.
[21] 肖媛, 崔国民, 李帅龙. 一种新的用于换热网络全局优化的强制进化随机游走算法[J]. 化工学报, 2016, 67(12): 5140-5147.XIAO Y, CUI G M, LI S L. A novel random walk algorithm with compulsive evolution for global optimization of heat exchanger networks[J]. CIESC Journal, 2016, 67(12): 5140-5147.
[22] ZHANG H, CUI G, XIAO Y,. A novel simultaneous optimization model with efficient stream arrangement for heat exchanger network synthesis[J]. Applied Thermal Engineering, 2017, 110: 1659-1673.
[23] BJÖRK K M, WESTERLUND T. Global optimization of heat exchanger network synthesis problems with and without the isothermal mixing assumption[J]. Computers & Chemical Engineering, 2002, 26(11): 1581-1593.
[24] BAGAJEWICZ M J. Global optimization of the stage-wise superstructure model for heat exchanger networks[J]. Industrial & Engineering Chemistry Research, 2015, 54(5): 1595-1604.
[25] LINNHOFF B, AHMAD S. Cost optimum heat exchanger networks(Ι): Minimum energy and capital using simple models for capital cost[J]. Computers & Chemical Engineering, 1990, 14(7): 729-750.
[26] ZHU X X, O’NEILL B K, ROACH J R,. A method for automated heat exchanger network synthesis using block decomposition and non-linear optimisation[J]. Chemical Engineering Research & Design, 1995, 73(A8): 919-930.
[27] LEWIN D R. A generalized method for HEN synthesis using stochastic optimization(Ⅱ): The synthesis of cost-optimal networks[J]. Computers & Chemical Engineering, 1998, 22(10): 1387-1405.
[28] PETTERSSON F. Synthesis of large-scale heat exchanger networks using a sequential match reduction approach[J]. Computers & Chemical Engineering, 2005, 29(5): 993-1007.
[29] YERRAMSETTY K M, MURTY C S. Synthesis of cost-optimal heat exchanger networks using differential evolution[J]. Computers & Chemical Engineering, 2008, 32(8): 1861-1876.
[30] HUO Z, ZHAO L, YIN H,. Simultaneous synthesis of structural-constrained heat exchanger networks with and without stream splits[J]. Canadian Journal of Chemical Engineering, 2013, 91(5): 830-842.
[31] 陈上, 崔国民, 彭富裕, 等. 采用动态更新策略的微分进化算法优化换热网络[J]. 热能动力工程, 2015, 30(4): 509-514.CHEN S, CUI G M, PENG F Y,. Optimization of the heat exchanger network by differential evolution algorithm based on dynamic update strategy[J]. Journal of Engineering for Thermal Energy and Power, 2015, 30(4): 509-514.
Optimization of heat exchanger network by random walk algorithm with compulsive evolution with structure-protection strategy
BAO Zhongkai, CUI Guomin, CHEN Jiaxing
(Institute of New Energy Science and Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)
A structure-protection strategy was proposed to eliminate the deficiency since structures with great evolutionary potentials could be substituted with bad solutions when random walk algorithm with compulsive evolution (RWCE) was applied to heat exchanger network optimization. A new population evolving in parallel with the original population was set to execute structure protection. Individuals in the new population are corresponded with ones in the original population and received their current optimal solutions to form a protective effect. Meanwhile, a novel evolution technique named as “dimensionality-reduction local search” was proposed for the new population. The technique determined the search dimension by controlling the update probability of each dimension, which could tap the evolutionary potentials of the protected solutions fully and thus improving the local search ability. Moreover, major evolution operations of RWCE were adopted by the original population and thus the strong global search ability was maintained. The RWCE with the structure-protection strategy was applied to optimize heat exchanger network with stream splits, some results superior to the reported ones were obtained, demonstrating that the proposed method possessed strong abilities in both the global and local search and improved the search quality.
random walk algorithm with compulsive evolution; structure-protection strategy; heat exchanger network; optimization
10.11949/j.issn.0438-1157.20170425
TP 18
A
0438—1157(2017)09—3522—10
2017-04-19收到初稿,2017-06-28收到修改稿。
崔国民。
鲍中凯(1993—),男,硕士研究生。
上海市科委部分地方院校能力建设计划项目(16060502600);国家自然科学基金项目(51176125)。
2017-04-19.
Prof. CUI Guomin, cgm@usst.edu.cn
supported by the Capacity Building Plan for Some Non-military Universities and Colleges of Shanghai Scientific Committee (16060502600) and the National Natural Science Foundation of China (51176125).
