混合多目标骨干粒子群优化算法在污水处理过程优化控制中的应用
2017-10-13周红标乔俊飞
周红标,乔俊飞
混合多目标骨干粒子群优化算法在污水处理过程优化控制中的应用
周红标1,2,3,乔俊飞1,2
(1北京工业大学信息学部,北京 100124;2计算智能和智能系统北京市重点实验室,北京 100124;3淮阴工学院自动化学院,江苏淮安 223003)
通过对污水生化处理过程的分析,选取能耗和罚款最低为优化目标,建立污水生化处理过程多目标优化控制模型。为了提高Pareto最优解集的收敛性和多样性,提出一种基于Pareto支配和分解的混合多目标骨干粒子群优化算法(HBBMOPSO)。该方法采用带自适应惩罚因子的分解方法选取个体引导者,采用Pareto支配和拥挤距离法维护外部档案和选取全局引导者。此外,采用精英学习策略增强粒子跳出局部Pareto前沿的能力。最后,将HBBMOPSO与自组织模糊神经网络预测模型和自组织控制器相结合,实现污水生化处理过程溶解氧和硝态氮设定值的动态寻优、智能决策和底层跟踪控制。利用国际基准仿真平台BSM1进行实验验证,结果表明所提HBBMOPSO方法在保证出水水质参数达标的前提下,能够有效降低污水处理过程的能耗。
污水;优化;过程控制;粒子群;分解
引 言
活性污泥法是城市污水处理厂普遍采用的污水生物处理方法[1-2]。该方法通过向废水中连续充入空气,经过一定反应时间后,因好氧微生物繁殖而形成活性污泥。利用活性污泥的生物凝聚、吸附和氧化作用,分解去除污水中的有机污染物[3]。为了满足出水排放标准,降低罚款(在国际基准模型中,一般利用出水水质来表征罚款),污水处理厂经常处于满负荷运行,即通过鼓风机和回流泵保持好氧区溶解氧(dissolved oxygen,O)浓度和厌氧区硝态氮(nitrate nitrogen,NO)浓度处于较高水平[4]。但是,鼓风机和回流泵的运转需要大量的能量供给,这不可避免地增加了运行成本。同时,从生化反应机理来看,只有合适的O和NO才能保证硝化和反硝化反应的顺利进行[5]。因此,应根据实际运行情况对O和NO的设定值进行动态寻优,构建以降低能耗(energy consumption,EC)和出水水质(effluent quality,EQ)为目标的多目标优化控制策略,从而提高污水处理效果和降低运行成本。
在过去的十几年里,单目标优化控制在污水处理过程中已取得了丰硕成果[6-8]。但是,单目标优化控制主要关注能耗指标,容易导致出水水质参数超标,增加运行成本。随后,有研究者通过权重因子构建损失函数将包含能耗和出水水质的多目标优化问题转换成单目标优化问题[9-11]。但是,这种方法不仅权重因子难以确定,而且难以取得能耗和出水水质之间的最佳平衡。多目标优化算法能够克服上述缺点。因此,污水处理过程的多目标优化控制受到了广泛关注[12-18]。文献[13]利用集成有多目标优化算法的交互式软件IND-NIMBUS构建污水处理过程全流程的运行优化模型。文献[14]采用NSGAII算法建立温室气体排放、操作成本和出水污染物浓度的多目标优化模型。文献[15]采用动态多目标优化算法建立开发成本和污水处理质量的两目标优化模型。文献[16-18]采用NSGAII算法建立能耗和出水水质的两目标优化模型。通过上述分析发现,在污水处理过程中采用多目标优化控制不仅能够保证出水水质参数达标,而且能够有效降低能耗和运行成本。但是上述研究对多目标优化算法的讨论和改进还存在不足,同时NSGAII算法运行成本较高,解的收敛性和多样性有待提高,能耗的降低还有一定的空间。
模拟鸟类觅食行为的粒子群优化(particle swarm optimization,PSO)算法[19]具有收敛速度快、概念简明和易于实现的优点,在多目标优化领域应用更加普遍[20-22]。但是传统粒子群优化算法在决策空间中探索和开发能力的平衡严重依赖于对飞行参数的调控[22],限制了其在实际工程中的应用。文献[23]提出的骨干粒子群优化(barebones particle swarm optimization,BBPSO)算法取消了速度更新公式,采用关于粒子个体引导者和全局引导者的高斯采样完成粒子位置更新,无须额外的参数设置,更加适合实际工程应用,因此有研究者将其扩展用于解决多目标优化问题[24-25]。
Pareto解集的收敛性和多样性是多目标优化算法面临的两个主要问题。目前,一般通过Pareto支配关系选取个体引导者以促进种群收敛,通过密度估计策略(如自适应网格[20]、拥挤距离[26]等)来保持种群多样性。文献[27]提出的MOEA/D方法采用分解策略将多目标优化问题分解成一组单目标优化问题,具有更低的计算复杂度、更好的收敛性和多样性。因此,有研究者将分解方法集成到多目标粒子群算法当中[28]。但是,同时考虑综合利用分解和Pareto支配的多目标粒子群优化算法的研究相对较少,尤其是在多目标骨干粒子群优化中未见相关报道。因此,本文同时利用Pareto支配和带自适应惩罚因子的分解方法来构建混合多目标骨干粒子群优化(hybrid barebones multi-objective particle swarm optimization,HBBMOPSO)算法,以期提高Pareto解集的收敛性和多样性,从而提供给决策者更高质量的候选解。
本文在分析污水处理过程控制变量、操作变量、优化目标和出水水质性能指标的基础上,首先利用前期研究的自组织模糊神经网络[29](self-organizing fuzzy neural network,SOFNN)建立EC、EQ和出水水质参数的目标函数;然后利用本文所提的HBBMOPSO算法对O和NO设定值进行动态寻优,并进一步利用智能决策系统选取偏好解作为当前优化周期的优化设定值;最后利用前期研究的SOFNN控制器[30]实现对优化设定值的底层跟踪控制。所有实验均采用活性污泥污水处理国际基准仿真平台(Benchmark Simulation Model No.1, BSM1)进行验证。
1 污水处理过程多目标优化问题
BSM1是由国际水质协会(IWAQ)和欧盟科学技术与合作组织(COST)合作开发,可用于公平评价不同控制策略和优化方法。BSM1采用典型的前置反硝化脱氮A/O工艺[31],由生化反应池和二沉池组成,如图1所示。生化反应池包含5个单元,前2个单元是缺氧区,主要完成反硝化反应,后3个单元是好氧区,主要完成硝化反应。生化反应池第3、4单元的氧气转换系数要求保持在恒定值240 d−1。由于入水流量和组分浓度呈现强非线性关系,O和NO控制器的目标就是分别通过调节第5单元的曝气量La5和内回流量a来控制第5单元的溶解氧浓度(O,5)和第2单元的硝态氮浓度(NO,2)[30-32]。多目标优化的目的就是分别通过动态调整O,5和NO,2的设定值[O,sp,NO,sp],实现EC和EQ之间的最佳平衡。
在污水处理过程中,O,5和NO,2设定值不仅影响EQ,而且与EC有密切关系。因此,为了取得EC和EQ之间的最佳平衡,利用HBBMOPSO算法来处理这对相互冲突的目标函数。
由于曝气能耗(AE)和泵送能耗(PE)占总能耗的70%以上[18],因此优化问题的EC定义为AE和PE之和,即
EC=AE+PE (1)
按照BSM1机理模型的定义,AE和PE为[31]
(3)
式中,V和Lai分别为第个单元的体积和氧气转换系数;O,sat为溶解氧饱和浓度;为优化周期;a、r和w分别为内回流量、污泥回流量和污泥排放量。
EQ表示向受纳水体排放出水污染物所需支付的罚款,按照BSM1定义,EQ的公式为[18,32]
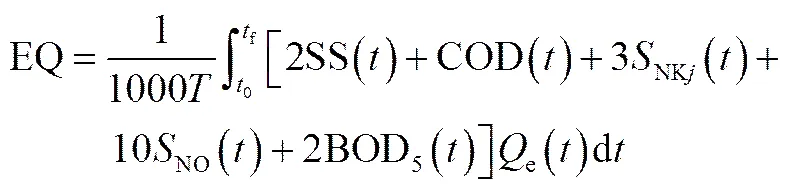
式中,SS、COD、NO、NKj和BOD5分别为固体悬浮物浓度、化学需氧量、硝态氮浓度、凯氏氮浓度和5日生化需氧量;e是上清液排出量。
出水水质参数的约束条件为BSM1基准中给出的达标限定值,具体为[18]

其中,出水总氮tot为出水硝态氮NO和出水凯氏氮NKj之和
综上所述,污水处理过程约束多目标优化问题描述如下

其中,=[1,2]=[O,sp,NO,sp]为优化向量;f()为出水水质参数与优化向量之间的关系,=1,2,…,5;和是第个优化变量的上下限,=1,2。
由式(1)~式(4)可以发现,EC主要与操作变量La5和a有关,EQ主要与5种出水水质参数有关。但是,EC、EQ与O,5、NO,2这两个优化变量之间并没有明确的数学关系,同时构成约束条件的关键出水水质参数也不能在线测量。因此,首先需要利用数据驱动思想建立EC、EQ和出水水质参数的精确软测量模型,作为优化目标函数;然后,采用多目标优化算法对O,5和NO,2进行动态寻优,获取一组等同优秀的Pareto解集;进一步,采用智能决策系统从Pareto解集选取偏好解作为优化设定值;最后,设计具有控制精度高和稳定性好的自适应控制器以跟踪优化设定值,从而实现多目标优化控制。本文构建的污水处理过程多目标优化控制整体架构如图1所示,其中自组织预测模型和自组织控制器的设计过程见文献[29-30],本文主要介绍多目标优化算法的设计。
BSM1模型自带晴好天气、阴雨天气和暴雨天气3种不同工况下入水流量和组分浓度的数据文件,采样间隔为15 min[31],来源于某实际污水处理厂连续两周的运行操作数据。图2所示为晴好天气下入水流量和入水S、B,H、NH浓度,能够反映污水处理过程强非线性、不确定性严重和强耦合的非线性特点[31-32]。
2 混合多目标骨干粒子群优化算法
下面首先阐述分解方法、引导者选择、外部档案维护、粒子位置更新和精英学习策略,然后给出HBBMOPSO算法的整体流程,最后给出污水生化处理过程优化控制的整体流程。
2.1 分解方法
MOEA/D采用分解方法将多目标优化问题分解为一系列单目标优化子问题,然后采用进化算法协同解决这些单目标子问题,主要方法有:加权和法、Tchebycheff法和基于惩罚的边界交集法(penalty-based boundary intersection,PBI)。研究表明,PBI方法具有更大的优势[27]。因此本文将PBI方法引入到BBMOPSO中,用于更新粒子的个体引导者,构建基于分解和支配相结合的混合多目标骨干粒子群算法(HBBMOPSO)。
在PBI方法中[27],单目标优化子问题定义为
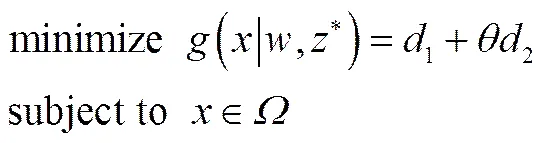
其中
式中,>0为惩罚参数,=(1,2,…,w)T为预定义的均匀分布的权向量集。PBI方法如图3所示,为理想参考点,为代表搜索方向的直线,为解()在上的投影,1为*和之间的距离,2为()和之间的垂直距离。
在PBI方法中,通常取为固定值5.0[27-28]。然而,最近的研究表明[33],值越小收敛速度越快,值越大多样性越好。文献[33]采用值随迭代次数线性增加策略,平衡了收敛性和多样性。本文提出了一个新的值非线性调整策略,公式如下

其中,的初始值为5,min1,max10;step=(max−min)/max。ΔEntropy为算法进化过程Pareto熵的变化量,由Pareto解映射到平行格坐标系统后得到,具体见文献[21]。用于区分进化状态的阈值由式(9)计算得到[21]
(9)
其中,为目标个数,为时刻档案中解的个数。
图4给出了本文算法在第2天第1个优化周期获得的Pareto熵及其变化量,图5给出了对应的值变化情况。可以看出,能够随着进化状态非线性调整,起到加快收敛速度和提高多样性的目的。
2.2 引导者选择
引导者选择包括个体引导者pbest和全局引导者gbest的更新:pbest采用分解的方法从外部档案选择,并且考虑约束条件的影响;gbest随机选自外部档案中具有较大拥挤距离的前10%的解。
pbest更新:对于当前粒子,根据解的可行性和权向量从外部档案中为其选择一个具有较低聚合函数值的解作为其个体引导者,具体流程见算法1。其中,对于粒子,其约束违背程度定义为

其中,g(),=1,2,…,为粒子的个不等式约束条件;h(),=+1,+2,…,为粒子的−个等式约束条件。
Algorithm 1:Update of pbest
for= 1 to
set pbest=1;
for= 2 to ||
if pbest&Aare feasible
if(pbest|w,*) >(A|w,*)
pbest=A;
end if
end if
if pbestis feasible&Ais infeasible
pbestremain;
end if
if pbestis infeasible&Ais feasible
pbest=A;
end if
if pbest&Aare infeasible
pbest=arg min cv(pbest,A);
end if
end for
end for
return pbest
2.3 粒子位置更新
粒子位置更新公式为[24]
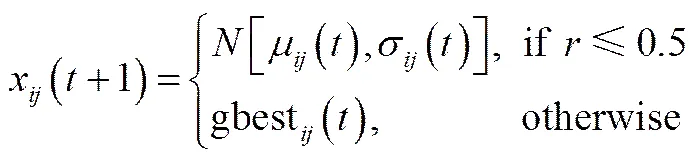
其中,μ() = [×pbest()+(1−)×gbest()]/2 和σ()=|pbest()−gbest()|,为[0,1]之间均匀分布的随机数。采用pbest和gbest的随机权重和作为高斯采样的中心,扩大了粒子的搜索范围;以50%的交叉概率继承全局引导者gbest的信息,算法更加注重对gbest的开发,提高了收敛速度。
2.4 外部档案维护
HBBMOPSO算法采用有限容量的外部档案来存储非支配解,需要采用合适的外部档案维护算法来提高解的多样性和收敛性。目前常用的有自适应网格法[20]和拥挤距离法[26],由于拥挤距离法无须设置额外参数,更加适合工程应用,本文采用拥挤距离法[26,33]来维护外部档案,具体流程见算法2。
假设为外部档案,为产生的新种群,a为外部档案的最大容量。在ArchiveUpdate算法中,CheckDominance(S,A)函数用于评价S和A之间的Pareto支配关系。当S支配A时,该函数返回1;否则,当A支配S或S和A互不支配时,返回−1;最终,算法将返回更新后的外部档案。
Algorithm 2:Update of External Archive
for= 1 to ||
for= 1 to ||
flag = CheckDominance(S,A);
if flag == 1
markAas a dominated solution;
else if flag == −1
markSas a dominated solution; break;
end if
end for
delete the marked dominated solutions from;
if Sis not marked as a dominated solution
addSto;
if || >N
compute the crowding distance;
delete the most crowded one;
end if
end if
end for
return
2.5 精英学习策略
为了克服粒子快速收敛特性带来的易陷入局部Pareto前沿的缺陷,MOPSO一般都带有粒子变异操作。但是,粒子变异算子难以弥补粒子搜索潜在的脆弱性[34],对于复杂的实际问题,种群容易陷入局部Pareto前沿。因此,设计了精英学习策略(elitism learning strategy,ELS)实现外部档案中非支配解的进化搜索[34-35],具体流程见算法3。
在算法3中,模拟二进制交叉(simulated binary crossover,SBX)操作用于精英解之间交换有用的基因片段,多项式变异(polynomial mutation,PM)操作通过产生一个小的扰动以对局部区域进行搜索。首先从外部档案中选择一定数目适应度值fitness(a,)较大的非支配解形成精英子集,本文的数目取||的一半。对于外部档案中每一个解A(=1,2,…, ||),在[1, ||]随机产生一个整数。然后,对A和E构成的父代解执行SBX操作产生子代解。最终从子代解1和2中随机选取一个执行PM操作,形成新的解S。
Algorithm 3:Elitism Learning
for= 1 to ||
generate a random integerin [1, ||];
{1,2} = SBX(A,E)
generate a random integerin [1, 2];
S= PM(C);
end for
return
2.6 HBBMOPSO算法整体流程
下面给出HBBMOPSO算法的整体流程,首先对粒子位置和参考点进行初始化,然后算法进入主循环进行迭代,直至满足停止条件,具体见算法4。
Algorithm 4: HBBMOPSO
initialize ev=0,=null, and={1,2,…,p};
generatewell-distributed weighted vectors;
for= 1 to
randomly generate the positionxofp;
evaluate the objective values ofp;
set pbest=pand initialize*;
end for
update external archive (Algorithm 2);
ev= ev +;
while ev≤ max_ev
environmental detecting using ΔEntropy
adaptively adjustusing Eq. (8)
for=1 to
select gbest(Algorithm 1);
update the positionxofpusing Eq. (11);
evaluate the objective values forp;
update pbest;
update the reference point* in Eq. (7);
end for
ev= ev +;
update external archive (Algorithm 2);
perform ELS (Algorithm 3);
evaluate new solutions’ objective values;
update the reference point* in Eq. (7);
update external archive (Algorithm 2);
ev= ev +;
end while
output
2.7 优化控制整体流程
污水处理过程多目标优化控制整体流程如下。
(1)利用BSM1基准离线产生500组建模数据,输入为O,5、NO,2和入水水质参数,输出为EC、EQ和出水水质参数;利用SOFNN[29]预测模型建立优化算法的目标函数。
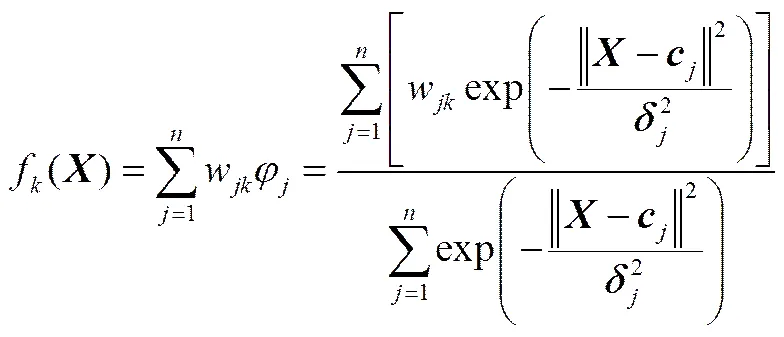
其中,=[1,2,…,x]为SOFNN的输入向量,为输入变量数;=[1j,2j,…,c]和=[1j,2j,…,δ]分别为规则层第个神经元对应的隶属函数层神经元的高斯函数中心和宽度;φ为规则层第个神经元归一化后的输出;w为规则层第个神经元与输出层第个神经元之间的连接权;=1,2,…,,为规则层神经元数;=1,2,…,,为输出变量数。SOFNN采用二阶算法优化中心、宽度和权值,采用奇异值分解优化网络结构,构建了结构紧凑、学习速度快和预测精度高的网络模型[29]。
(2)利用所提的HBBMOPSO算法(Algorithm 4)对EC、EQ和出水水质参数的目标函数进行优化,得到一组Pareto最优解集。
(3)利用模糊隶属函数法设计智能决策系统,从包含众多等同优秀解的Pareto解集中选取一个偏好解,以确定当前优化周期内O,5和NO,2的底层跟踪控制设定值。
对于第个目标函数F,外部储备集中非支配解的满意度定义为
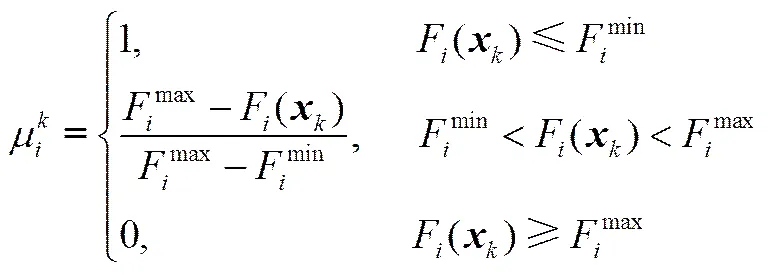
其中,max和min分别是第个目标函数F的最大值和最小值。归一化的非支配解的满意度为
(14)
其中,为目标个数,|A|为外部储备集元素个数。选取μ的最大值对应的解为偏好解。
(4)利用基于互信息的自组织模糊神经网络控制器对[O,sp,NO,sp]优化设定值进行跟踪控制,控制器在复杂工况的自适应能力有一定程度提高[30]。若BSM1连续14天数据仿真完毕,则结束;否则,返回步骤(2)进行下一个优化周期的优化控制。
3 实验验证
3.1 参数设置
所有实验均在BSM1基准仿真平台上进行,控制器采样周期为45 s,优化周期为2 h,O,5和NO,2的优化设定值范围分别为0.4~3和0.2~2 mg·L−1。对于HBBMOPSO算法,种群规模为50,外部档案规模a为50,目标函数最大评价次数ev为10000(即最大迭代次数max=200),交叉概率c为0.9,变异概率m为1/,SBX和PM的分布性指数c和m均为20。
3.2 结果和分析
图6给出了分别利用SOFNN和FNN预测模型得到的能耗EC和出水水质EQ的预测结果。可以看出,SOFNN的预测精度要比FNN更高,为多目标优化算法提供了更精确的目标函数。图7给出了第2 d第1个优化周期HBBMOPSO算法在固定、线性递增和自适应3种情况下的逼近Pareto前沿。可以看出,自适应获取的Pareto解收敛性和多样性更好。图8给出了HBBMOPSO与NSGAII、dMOPSO、BBMOPSO算法获得的第2 d第1个优化周期的Pareto最优解集以及决策系统决策出的偏好解。从图7可以看出,本文算法获取的Pareto前沿的收敛性和分布性更好,获取的优化设定值具有更低的EC和EQ。
图9给出了7 d的设定值优化情况和底层SOFNN自组织控制器跟踪效果。从图9可以看出,在优化控制过程中,O,sp和NO,sp随着入水条件和组分浓度的变化进行动态调节,实现了出水水质和能耗这对冲突目标之间的动态平衡;同时,SOFNN控制器的控制效果要明显优于PID控制,尤其是硝态氮的控制精度有明显的提升,实现了复杂工况下的快速高精度的跟踪控制。
图10给出了多目标优化控制过程出水水质参数变化情况。从图10可以看出,相比于PID恒定值控制,优化控制方法下,NH浓度没有观察到明显上升趋势,tot浓度总体呈现下降趋势。另外,BOD5、COD和TSS基本维持不变,表明优化控制在有效降低能耗的同时并没有引起出水水质参数超标而造成罚款上升的情况。从污水处理过程机理分析可知,tot和NH是一对具有相互竞争关系的出水水质参数,通过多目标优化算法能够取得这两者之间的最佳平衡。
表1给出了晴好天气工况下不同优化控制策略获得的AE、PE、EC和EQ的具体情况。其中,influent表示平均入水水质参数;PID表示恒定值控制,即O,5和NO,2分别取2和1 mg·L−1;SOOC表示单目标优化控制;Hopfield表示采用文献[9]介绍的Hopfield神经网络实现的多目标优化控制;DDAOC表示采用文献[11]介绍的自适应动态规划方法实现的多目标优化控制;NSGAII表示采用文献[18]介绍的神经网络和多目标优化算法相结合的优化控制;dMOPSO表示采用文献[28]介绍的基于分解的多目标优化算法,BBMOPSO表示采用文献[24]介绍的多目标骨干粒子群算法,这两者的参数均按照原文设置。从表1可以看出,相比PID恒定值控制,在晴好天气工况下,HBBMOPSO方法的EC下降9.60%,并且EQ上升幅度较小。实验结果表明HBBMOPSO方法不仅能够保证出水水质参数达标,而且能够有效降低能耗。同时,与dMOPSO和BBMOPSO相比,优化效果有较大程度的提升,表明了带有自适应惩罚参数的混合多目标骨干粒子群算法能够获取更高质量的解。此外,NSGAII方法的EQ上升幅度较大,主要是由于出水tot较大引起。单目标优化SOOC方法的EC下降较小,节能效果不太明显。对表进一步分析,可以看出,HBBMOPSO方法下的NH略有上升,tot有较大程度下降,其他水质参数变化幅度不大,这与图7水质参数变化情况相吻合。需要指出的是,本文所有对比方法均能够保证平均出水水质参数符合达标限定值。从出水污染物去除率的角度分析,采用HBBMOPSO优化控制方法,相比入水水质参数,出水NH、tot、BOD5、COD和TSS的去除率分别达到了92.30%、72.61%、96.29%、71.66%和93.74%。

表1 晴好天气不同优化控制策略的能耗和出水水质比较
① Results are listed in original papers.
为了进一步验证HBBMOPSO优化方法在复杂天气工况下的适应能力,利用BSM1基准模型中的阴雨和暴雨两种工况的数据文件进行了实验验证,表2给出了不同优化控制策略的对比结果。从表2可以看出,相比PID恒定值控制,在阴雨和暴雨天气工况下,HBBMOPSO的EC分别下降了9.29%和8.77%,并且EQ没有明显上升。相比NSGAII、dMOPSO和BBMOPSO,HBBMOPSO优化方法的能耗更低,表明HBBMOPSO在复杂工况下也能够取得良好的节能效果。
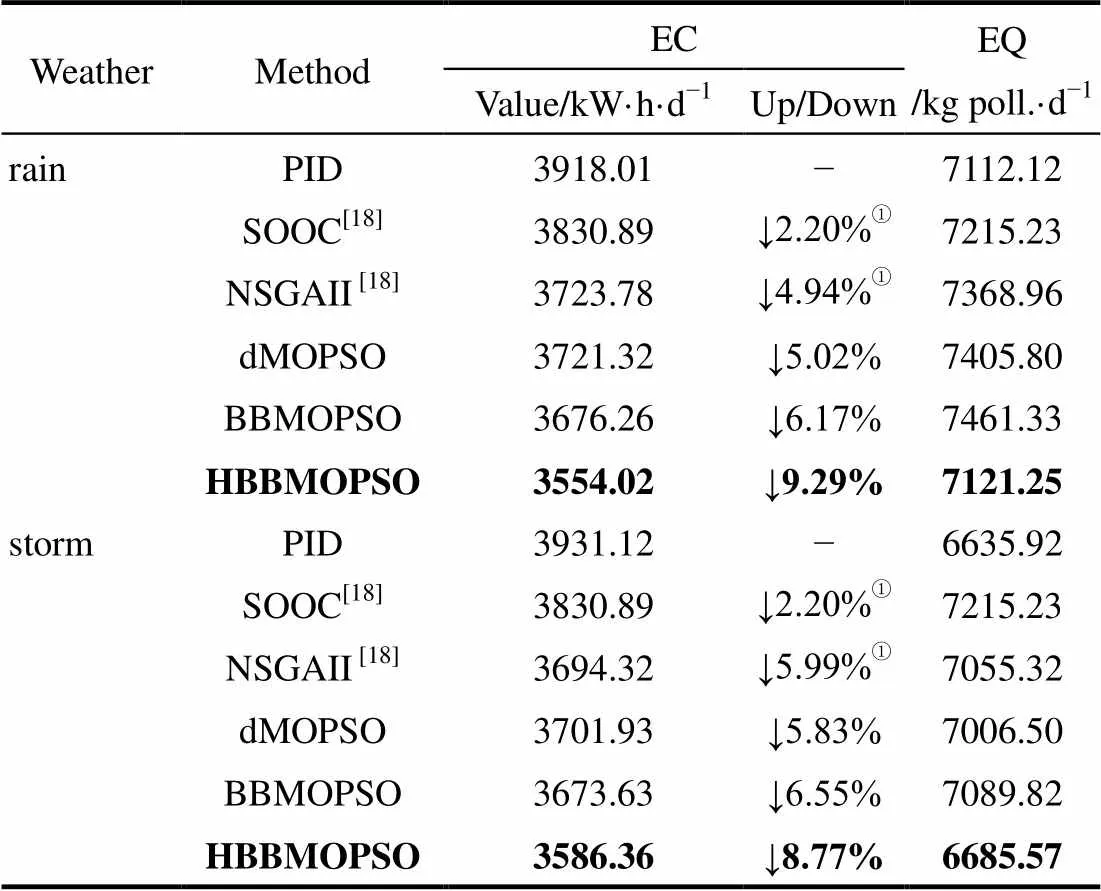
表2 阴雨和暴雨天气不同优化控制策略的EC和EQ比较
①Results are listed in original papers.
4 结 论
针对活性污泥法污水处理过程能耗和罚款最低的多目标优化问题,提出了混合多目标骨干粒子群优化(HBBMOPSO)算法。该方法将Pareto支配和分解策略相结合,利用分解策略选取个体引导者,利用拥挤距离和Pareto支配关系维护外部档案和选取全局引导者。同时,设计了分解方法中惩罚参数的自适应调整策略,提高了算法收敛速度和非支配解的质量。此外,设计了外部档案精英学习策略,提高了种群跳出局部Pareto前沿的能力。将HBBMOPSO算法与自组织模糊神经网络预测模型、自组织控制器相结合,实现了污水处理过程多目标优化运行控制。
与单目标优化、NSGAII、dMOPSO和BBMOPSO等方法相比,HBBMOPSO方法的寻优能力更强,克服了传统粒子群优化算法对飞行参数敏感的不足,获取的Pareto最优解的收敛性和多样性均有较大程度的改善,为智能决策系统提供了一组质量更高的候选解。利用智能决策系统选取的偏好解在保证出水水质参数达标的前提下,取得了更低的能耗。此外,实验结果还表明,自组织模糊神经网络构建的能耗和出水水质优化目标模型具有较高的建模精度,自组织控制器能够较快地跟踪优化设定值,具有较好的稳定性、鲁棒性和控制精度,能够满足多目标优化控制的需求。
下一步的研究工作是充分挖掘污水处理过程蕴含的知识信息,将其与过程数据相结合,构建基于知识和数据混合驱动的污水生化处理过程多目标优化运行控制策略。
References
[1] WAN J F, GU J, ZHAO Q,. COD capture: a feasible option towards energy self-sufficient domestic wastewater treatment[J]. Scientific Reports, 2016, 6(4): 1-9.
[2] OTURAN M A, AARON J J. Advanced oxidation processes in water/wastewater treatment: principles and applications. A review[J]. Critical Reviews in Environmental Science and Technology, 2014, 44(23): 2577-2641.
[3] SANTÍN I, PEDRET C, VILANOVA R,. Removing violations of the effluent pollution in a wastewater treatment process[J]. Chemical Engineering Journal, 2015, 279(11): 207-219.
[4] JUDD S J. The status of industrial and municipal effluent treatment with membrane bioreactor technology[J]. Chemical Engineering Journal, 2016, 305(12): 37-45.
[5] ÅMAND L, CARLSSON B. Optimal aeration control in a nitrifying activated sludge process[J]. Water Research, 2012, 46(7): 2101-2110.
[6] HREIZ R, LATIFI M A, ROCHE N. Optimal design and operation of activated sludge processes: state-of-the-art[J]. Chemical Engineering Journal, 2015, 281(12): 900-920.
[7] OSTACE G S, BAEZA J A, GUERRERO J,. Development and economic assessment of different WWTP control strategies for optimal simultaneous removal of carbon, nitrogen and phosphorus[J]. Computers and Chemical Engineering, 2013, 53(6): 164-177.
[8] SANTIN I, PEDRET C, VILANOVA R. Applying variable dissolved oxygen set point in a two level hierarchical control structure to a wastewater treatment process[J]. Journal of Process Control, 2015, 28(4): 40-55.
[9] 韩广, 乔俊飞, 韩红桂, 等. 基于Hopfield神经网络的污水处理过程优化控制[J]. 控制与决策, 2014, 29(11): 2085-2088. HAN G, QIAO J F, HAN H G,. Optimal control for wastewater treatment process based on Hopfield neural network[J]. Control and Decision, 2014, 29(11): 2085-2088.
[10] MACHADO V C, GABRIEL D, LAFUENTE J,. Cost and effluent quality controllers design based on the relative gain array for a nutrient removal WWTP[J]. Water Research, 2009, 43(20): 5129-5141.
[11] QIAO J F, BO Y C, CHAI W,. Adaptive optimal control for a wastewater treatment plant based on a data-driven method[J]. Water Science and Technology, 2013, 67(10): 2314-2320.
[12] DAI H L, CHEN W L, LU X W. The application of multi-objective optimization method for activated sludge process: a review[J]. Water Science and Technology, 2016, 73(2): 223-235.
[13] HAKANEN J, SAHLSTEDT K, MIETTINEN K. Wastewater treatment plant design and operation under multiple conflicting objective functions[J]. Environmental Modelling and Software, 2013, 46(4): 240-249.
[14] SWEETAPPLE C, FU G T, BUTLER D. Multi-objective optimisation of wastewater treatment plant control to reduce greenhouse gas emissions[J]. Water Research, 2014, 55(2): 52-62.
[15] HREIZ R, ROCHE N, BENYAHIA B,. Multi-objective optimal control of small-size wastewater treatment plants[J]. Chemical Engineering Research and Design, 2015, 102(7): 345-353.
[16] CHEN W L, LU X W, YAO C H. Optimal strategies evaluated by multi-objective optimization method for improving the performance of a novel cycle operating activated sludge process[J]. Chemical Engineering Journal, 2015, 260(9): 492-502.
[17] ZHANG R, XIE W M, YU H Q,. Optimizing municipal wastewater treatment plants using an improved multi-objective optimization method[J]. Bioresource Technology, 2014, 157(2): 161-165.
[18] QIAO J F, ZHANG W. Dynamic multi-objective optimization control for wastewater treatment process[J]. Neural Computing and Applications, 2016, 28(10): 1-11.
[19] KENNEDY J, EBERHART R C. Particle swarm optimization[C]// Proceeding of IEEE International Conference on Neural Networks. 1995: 1942-1948.
[20] COELLO C A C, PULIDO G T, LECHUGA M S. Handling multiple objectives with particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 256-279.
[21] HU W, YEN G G. Adaptive multiobjective particle swarm optimization based on parallel cell coordinate system[J]. IEEE Transactions on Evolutionary Computation, 2015, 19(1): 1-18.
[22] TRIPATHI P K, BANDYOPADHYAY S, PAL S K. Multi-objective particle swarm optimization with time variant inertia and acceleration coefficients[J]. Information Sciences, 2007, 177(22): 5033-5049.
[23] KENNEDY J. Bare bones particle swarms[C]// Proceedings of IEEE Swarm Intelligence Symposium. 2003: 80-87.
[24] ZHANG Y, GONG D W, DING Z H. A bare-bones multi-objective particle swarm optimization algorithm for environmental/economic dispatch[J]. Information Sciences, 2012, 192(6): 213-227.
[25] ZHANG Y, GONG D W, GENG N,. Hybrid bare-bones PSO for dynamic economic dispatch with valve-point effects[J]. Applied Soft Computing, 2014, 18(5): 248-260.
[26] DEB K, PRATAP A, AGARWAL S,. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.
[27] ZHANG Q F, LI H. MOEA/D: a multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731.
[28] ZAPOTECAS MARTÍNEZ S, COELLO COELLO C A. A multi-objective particle swarm optimizer based on decomposition[C]// Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation. 2011: 69-76.
[29] 乔俊飞, 周红标. 基于自组织模糊神经网络的出水总磷预测[J]. 控制理论与应用, 2017, 34(2): 224-232. QIAO J F, ZHOU H B. Prediction of effluent total phosphorus based on self-organizing fuzzy neural network[J]. Control Theory and Applications, 2017, 34(2): 224-232.
[30] 周红标. 基于自组织模糊神经网络的污水处理过程溶解氧控制[J]. 化工学报, 2017, 68(4): 1516-1524. ZHOU H B. Dissolved oxygen control of the wastewater treatment process using self-organizing fuzzy neural network[J]. CIESC Journal, 2017, 68(4): 1516-1524.
[31] JEPPSSON U, PONS M N. The COST benchmark simulation model-current state and future perspective[J]. Control Engineering Practice, 2004, 12(3): 299-304.
[32] HAN H G, QIAN H H, QIAO J F. Nonlinear multiobjective model-predictive control scheme for wastewater treatment process[J]. Journal of Process Control, 2014, 24(3): 47-59.
[33] YANG S X, JIANG S Y, JIANG Y. Improving the multiobjective evolutionary algorithm based on decomposition with new penalty schemes[J]. Soft Computing, 2016, 21(2): 1-15.
[34] LIN Q Z, LI J Q, DU Z H,. A novel multi-objective particle swarm optimization with multiple search strategies[J]. European Journal of Operational Research, 2015, 247(3): 732-744.
[35] LIN Q Z, CHEN J Y, ZHAN Z H,. A hybrid evolutionary immune algorithm for multiobjective optimization problems[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(5): 711-729.
Optimal control of wastewater treatment process using hybrid multi-objective barebones particle swarm optimization algorithm
ZHOU Hongbiao1,2,3, QIAO Junfei1,2
(1Faculty of Information Technology,Beijing University of Technology, Beijing 100124, China;2Beijing Key Laboratory of Computational Intelligence and Intelligent System, Beijing 100124, China;3Faculty of Automation, Huaiyin Institute of Technology, Huai’an 223003, Jiangsu, China)
Through analysis of biological wastewater treatment process (WWTP), a multi-objective optimal control strategy was developed with targets of minimizing both energy consumption and amercement. A hybrid multi-objective barebones particle swarm optimization (HBBMOPSO) algorithm based on Pareto dominance and decomposition was proposed to improve convergence and diversity of optimized set of Pareto solutions. In HBBMOPSO, selection of personal leaders was determined from self-adaptive penalty factor decomposition while maintenance of external dossiers and selection of global leaders were determined from dominance and crowded distance. Furthermore, elitism learning strategy was adopted to facilitate particle escaping from local Pareto fronts. Finally, HBBMOPSO was combined with self-organizing fuzzy nerve network modeler and controller to realize dynamic optimization, intelligent decision, and background monitoring on dissolved oxygen and nitrate nitrogen in biological WWTP. Experimental study on international standardized simulator platform BSM1 showed that HBBMOPSO method can effectively reduce energy consumption under the premise of ensuring effluent to meet quality standard.
wastewater; optimization; process control; particle swarm; decomposition
10.11949/j.issn.0438-1157.20170583
TP 273
A
0438—1157(2017)09—3511—11
2017-05-09收到初稿,2017-06-05收到修改稿。
乔俊飞。
周红标(1980—),男,博士研究生。
国家自然科学基金重点项目(61533002)。
2017-05-09.
Prof. QIAO Junfei, junfeiq@bjut.edu.cn
supported by the State Key Program of National Natural Science Foundation of China (61533002).
