基于优化灰色模型的紫金山排土场边坡位移预测研究
2017-10-13孙世国
孙世国,王 超,赵 娟
(1.北方工业大学 土木工程学院,北京 100144;2.三峡大学 土木与建筑学院,湖北 宜昌 443002)
基于优化灰色模型的紫金山排土场边坡位移预测研究
孙世国1,王 超1,赵 娟2
(1.北方工业大学 土木工程学院,北京 100144;2.三峡大学 土木与建筑学院,湖北 宜昌 443002)
针对外界干扰对边坡变形预测精度影响较大的问题,从理论出发,通过对累加后递增序列数据拟合的优化,加入符合边坡变形特征的线性与非线性因素再拟合;考虑边坡变形的复杂性以及外界因素影响,引入滚动序列算法,以优化灰色模型,并结合紫金矿排土场边坡实例,证明优化后灰色模型预测的应用价值。
灰色模型;滚动序列;数据拟合;变形预测
Abstract:In view of the problem that the external disturbance has great influence on the prediction precision of the slope deformation, from the theory itself, through the optimization of the cumulative incremental sequence data fitting, adding the linear and non-linear factors which conform to the slope deformation characteristics, considering the complexity of the slope deformation and the influence of the external factors, the rolling sequence algorithm is introduced to optimize the grey model, and the application value of the optimized grey model is proved by combining with the example of the slope of the purple gold deposit.
Keywords:gray model; rolling sequence; data fitting; deformation forecast
滑坡的预测预报研究是边坡工程中一直探索的课题,因为地质体本身的复杂性、人类生产活动以及环境因素的影响,致使滑坡的影响因子具有模糊性,为滑坡的预测研究带来诸多困难。近几十年来,国内外很多专家和学者对于滑坡的预测预报机理和方法进行了较多研究,如神经网络法预测、信息模型法预测、时间序列分析法预测、灰色系统理论模型预测、分形理论、混沌理论等等,以及近些年研究的组合模型。莫林辉等人[1]将灰色模型、灰色幂模型和幂函数回归模型进行组合,分别建立最优定权组合预测模型和最优非负变权系数组合预测模型,对湖南省某高速公路隧道口高边坡变形进行预测,成功地进行了较准确的预报;孙世国、苏振华等[2]将ARMA时间序列法和灰色模型进行组合,对某矿山边坡变形进行预测,结果证明该预测方法提高了较长预测步长的预测精度。显然,组合模型相对于单一的预测模型具有更高的预测精度和稳定性。
在实际边坡变形预测的研究中,灰色理论在预测坡体变形上得到了广泛的应用,其原因是灰色模型能够在信息量缺乏的情况下探索这些信息的变化规律,科学预测未来的发展趋势,预测的精度也相对较好。很多边坡的地质条件和变形机制相对复杂,各影响因子间时空效应和交互效应不能准确描述,致使传统的灰色模型不能准确地预测滑坡的发生,且方法上具有局限性。周英[3]通过改进传统灰色模型,考虑到时序不等、基坑的空间效应因素,对灰色模型进行改进,能够较为准确实现某基坑变形的中短期预测;王朝阳等[4]基于灰色模型理论,引入新陈代谢思想,成功地对向加坡和链子崖危岩体的变形进行预测,预测效果较好;孙世国等[5]通过改进灰色模型,对模型结构的灰参数进行二次拟合,基于监测数据成功地预测了丁家坟滑体变形情况。本文立足实现增加预测步长,从边坡变形规律和特点出发,动态调整模型算子来优化灰色模型,并结合紫金矿排土场边坡工程实际应用情况,对预测结果进行分析。
1 灰色模型理论
1.1传统的灰色模型
邓聚龙教授于1982年提出灰色系统理论[6],将离散型原始数据序列进行处理,使其成为有一定规律的数列再建立模型,以实现数据的预测。灰色模型中的GM(1,1)模型是预测分析的主要模型[7]。研究表明,边坡系统不断地与外界进行物质和能量交换,使得研究者对于整个边坡系统的认识具有局限性和模糊性特点。常用的方法是通过不断改进监测技术[8],以提高监测数据的精度,从而做出更准确预测。传统GM(1,1)模型建模的基本理论和计算公式可参考文献[9]。
1.2滚动序列
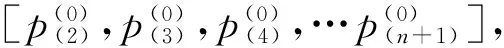
1.3优化的灰色模型
假设初始序列为p(0),累加数列为p(1),u、v为模型的灰参数,P(1)为模型的响应解。
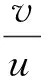
p(1)(t)=Ae-u(t-1)+B
(1)
为了提高预测模型的精度,可通过对式(1)重新拟合,使预测模型更为优化。
令
p(1)(t)=c1e-ut+c2+c3t+c4t2+…
(2)
写成矩阵形式为:
P(1)=J*C
(3)
由最小二乘法可得:
C= (JTJ)-1JTP(1)
(4)
优化后预测模型为:
P(0)(t+1) =P(1)(t+1) —P(1)(t)
(5)
1.4精度检验
常用的灰色预测模型的精度检验一般有关联度检验、残差检验和后验差检验三种检验方法,其中后验差精度检验方法在实际工程中应用较多,它由后验差c和小误差概率w共同描述。具体计算方法参考文献[11]。
2 工程实例研究
2.1工程概况
紫金山金铜矿地处福建省龙岩市,隶属于武夷山南脉,构造侵蚀中低山,矿区总体地势自东北向西南倾斜,交通便利,公路、铁路运输发达,于1993年组织开采,高差最大有888 m,属于高陡边坡。岩石受风化蚀变强烈,具分带性,构造运动强烈,稳定性较差,且区内水系较发育,地形复杂。具体工程地质条件见参考文献[12]。为了指导工程施工、反馈设计需要对矿区排土场边坡进行稳定性监测,由于监测点较多,本文以该矿区排土场边坡相对不稳定区域的JC815、JC910号监测点2013年12月6日至2014年7月18日水平位移监测数据为例进行预测分析,详细监测数据见表1。
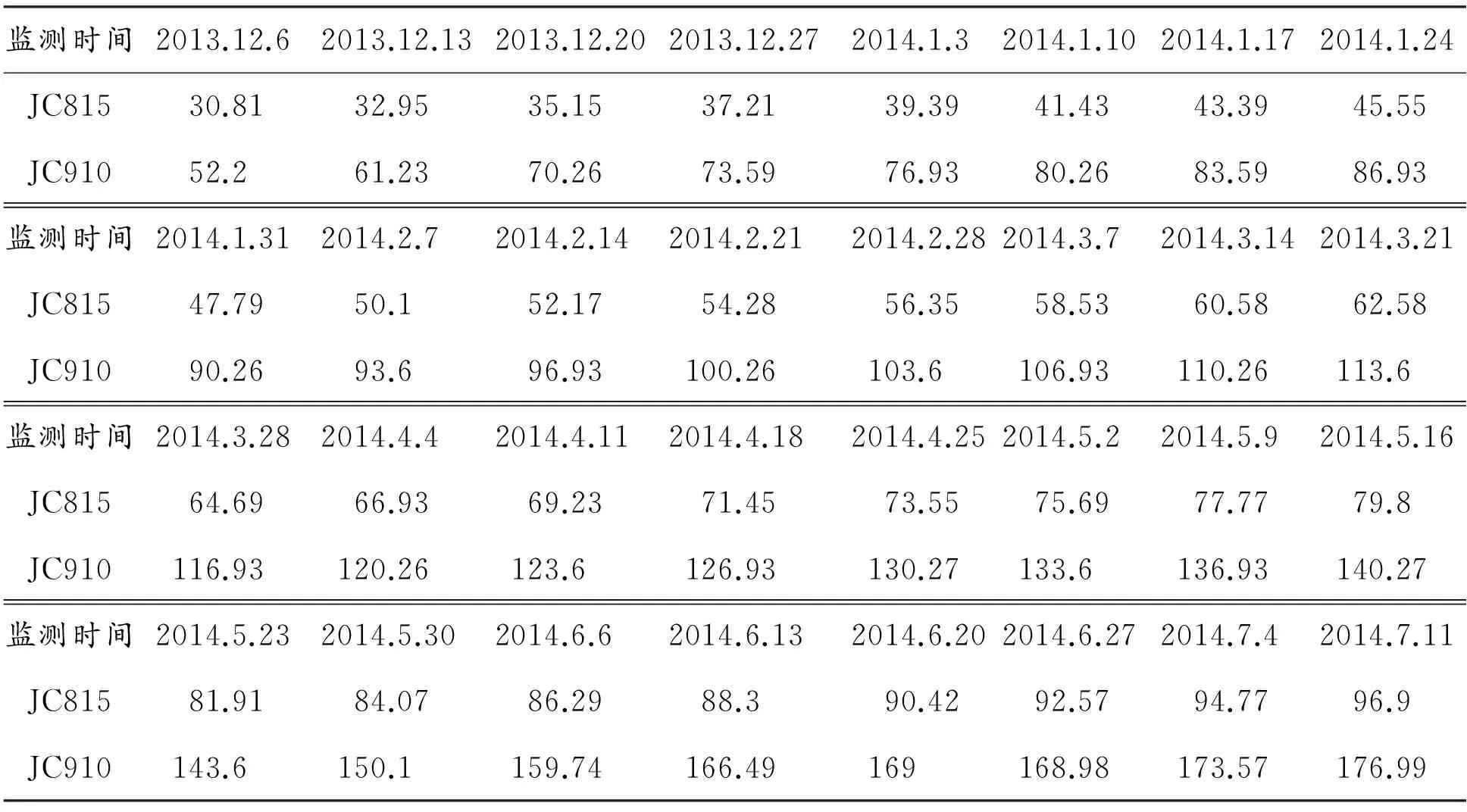
表1 JC815、JC910监测点X方向位移监测数据 mm
2.2边坡位移预测分析
使用灰色模型建模之前需对离散数列进行级比和光滑性检验[13],经分析满足建模要求,因此,本例以初始9组数据作为序列初始算子,运用优化后的灰色模型对紫金山金铜矿排土场边坡JC815、JC910号监测点X方向位移进行预测,并对比传统灰色模型,模型通过matlab数值分析软件编写计算代码,预测结果见表2、表3。
预测模型的检验精度均为“好”,符合预测要求,且两种预测模型选取了9组监测数据作为初始样本数列,由于matlab默认多项式最高次数项系数不为0,为获得更优预测值,经对比,本例m值为4,从表2、表3预测结果可以看出,优化后的灰色模型比传统灰色模型预测值更接近实测值,预测精度更高,误差更小,更具有实际应用价值。
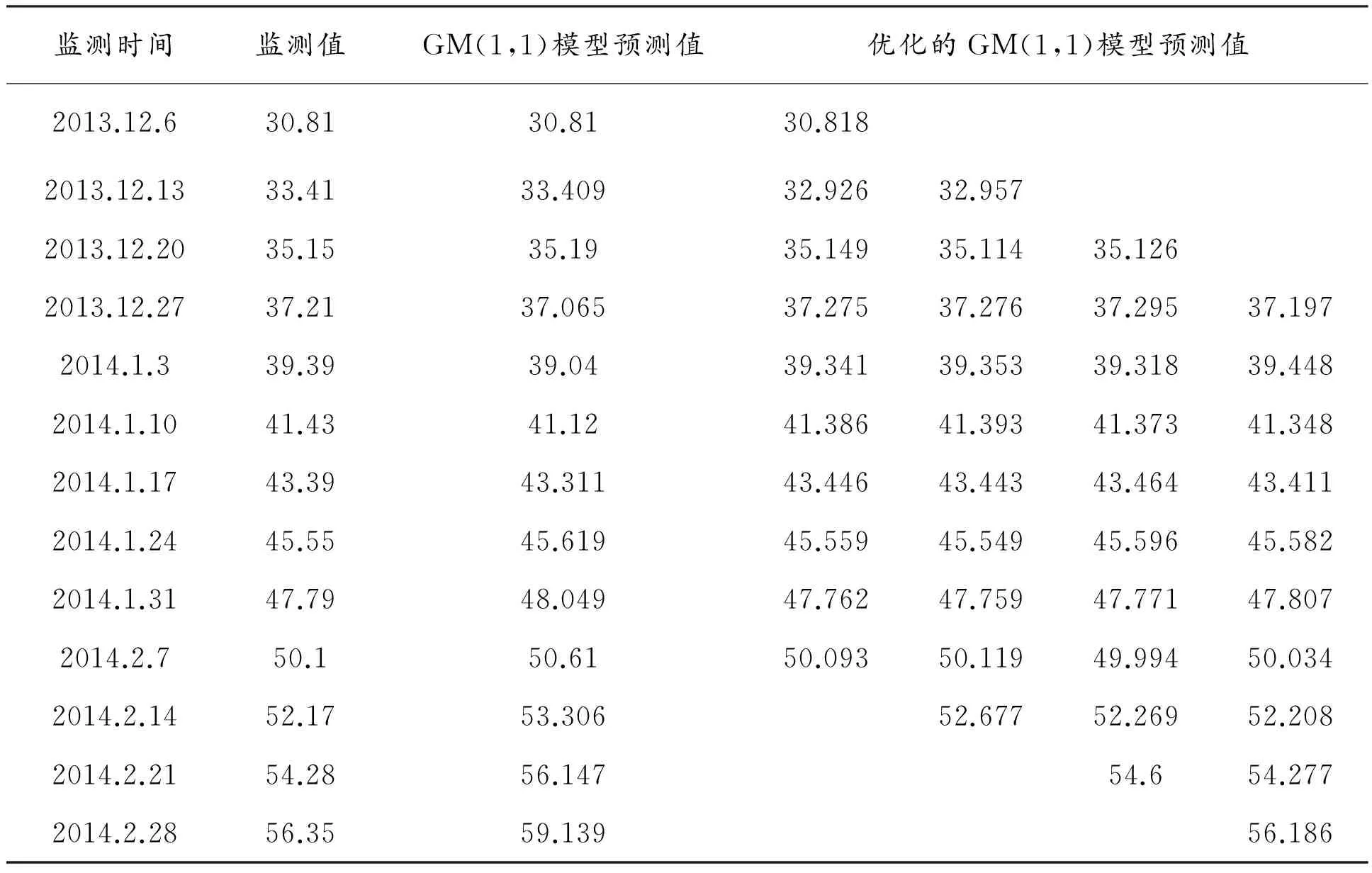
表2 JC815点X向位移预测 mm
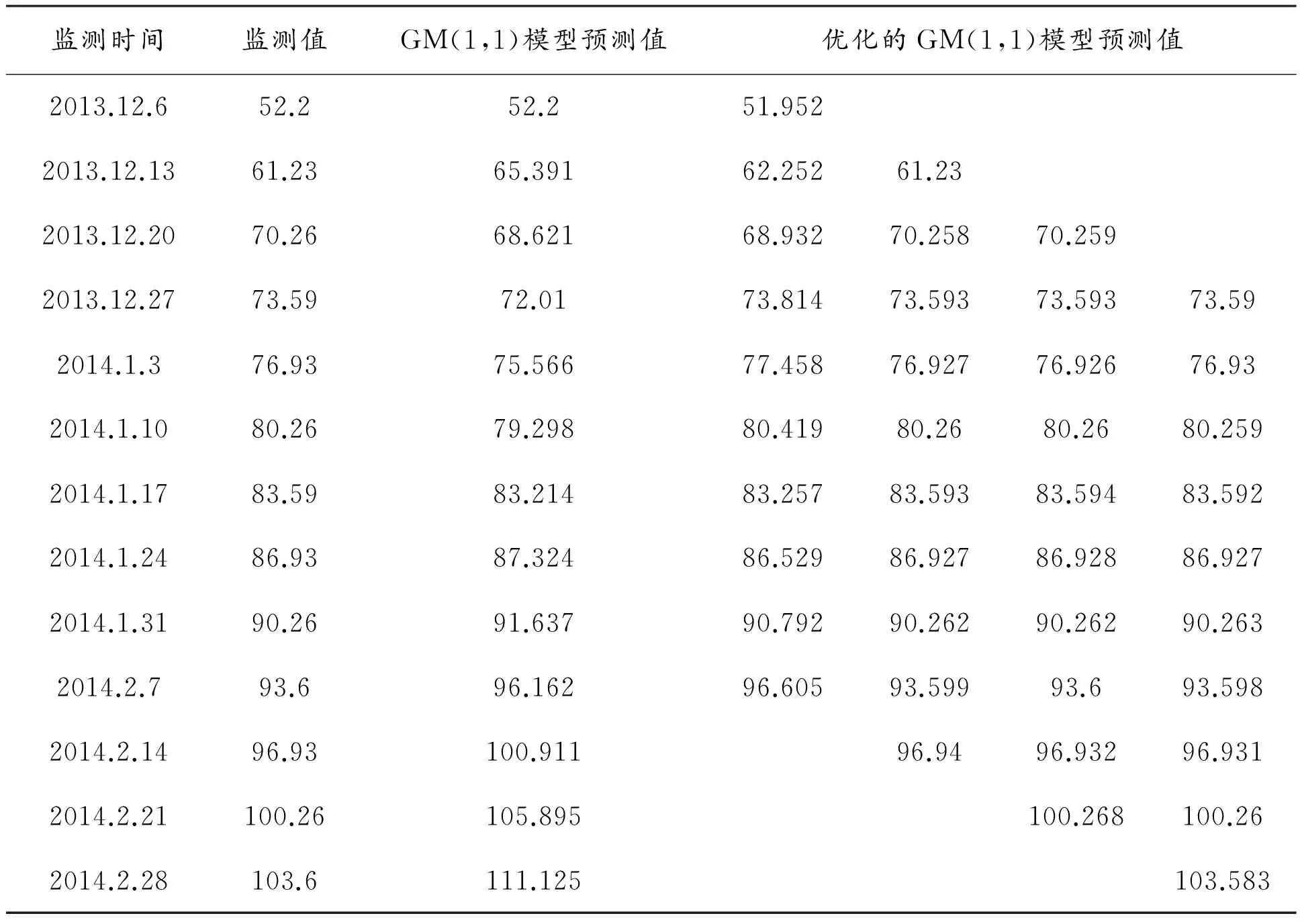
表3 JC910点X向位移预测 mm
以2014.1.3~2014.2.28的9组监测值作为初始样本数列,并对比传统的灰色模型、灰色新陈代谢模型、优化后的灰色模型和实际监测值,绘制成预测曲线,如图1、图2所示。
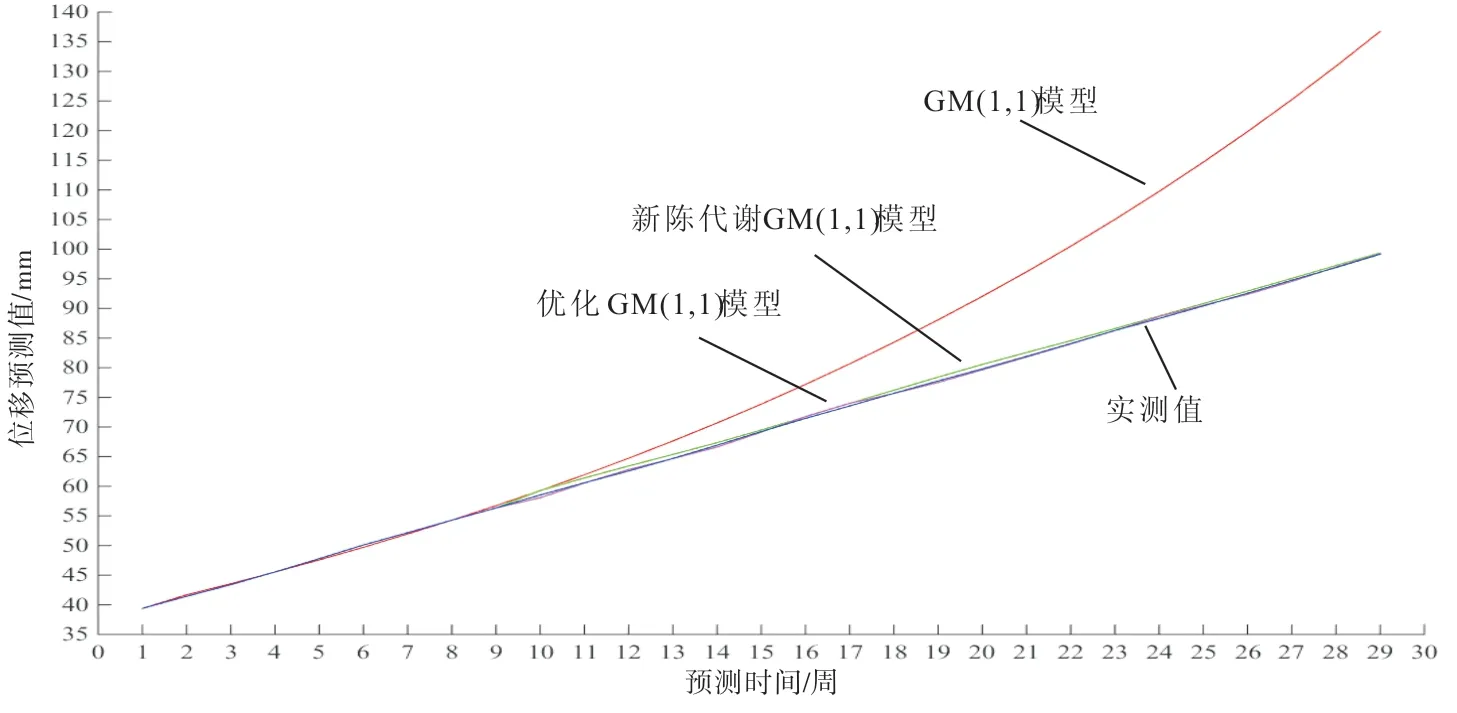
图1 JC815号监测点X向位移预测曲线
图2 JC910号监测点X向位移预测曲线
由图1、图2预测结果可以看出,传统灰色模型预测精度显然较低,与实测值之间残差相对较大,而新陈代谢GM(1,1)模型与本文优化的GM(1,1)模型拟合效果较好,残差值较小,在预测的前21周由于排土场X方向位移变化接近线性发展,优化后的模型能够完全拟合实测值,21周后边坡的变形有明显突增的趋势,新陈代谢GM(1,1)模型和优化后的灰色模型能够应对这种变化及时做出调整,变形曲线存在明显变化,其中JC815、JC910两测点处优化的GM(1,1)模型预测值的最大残差绝对值分别为0.45 mm、4.7 mm,相对于新陈代谢GM(1,1)模型0.82 mm、7.32 mm误差要小,预测效果更好。
图1与图2表示在系统及时更新监测数据时,模型能够读取最新的监测值参与预测,当系统未能及时置入新的监测值时,模型可以自适应依据最新的预测值以同样的方法进行样本的调整,从而达到中长期预测的目的,长期预测结果如图3、图4所示。
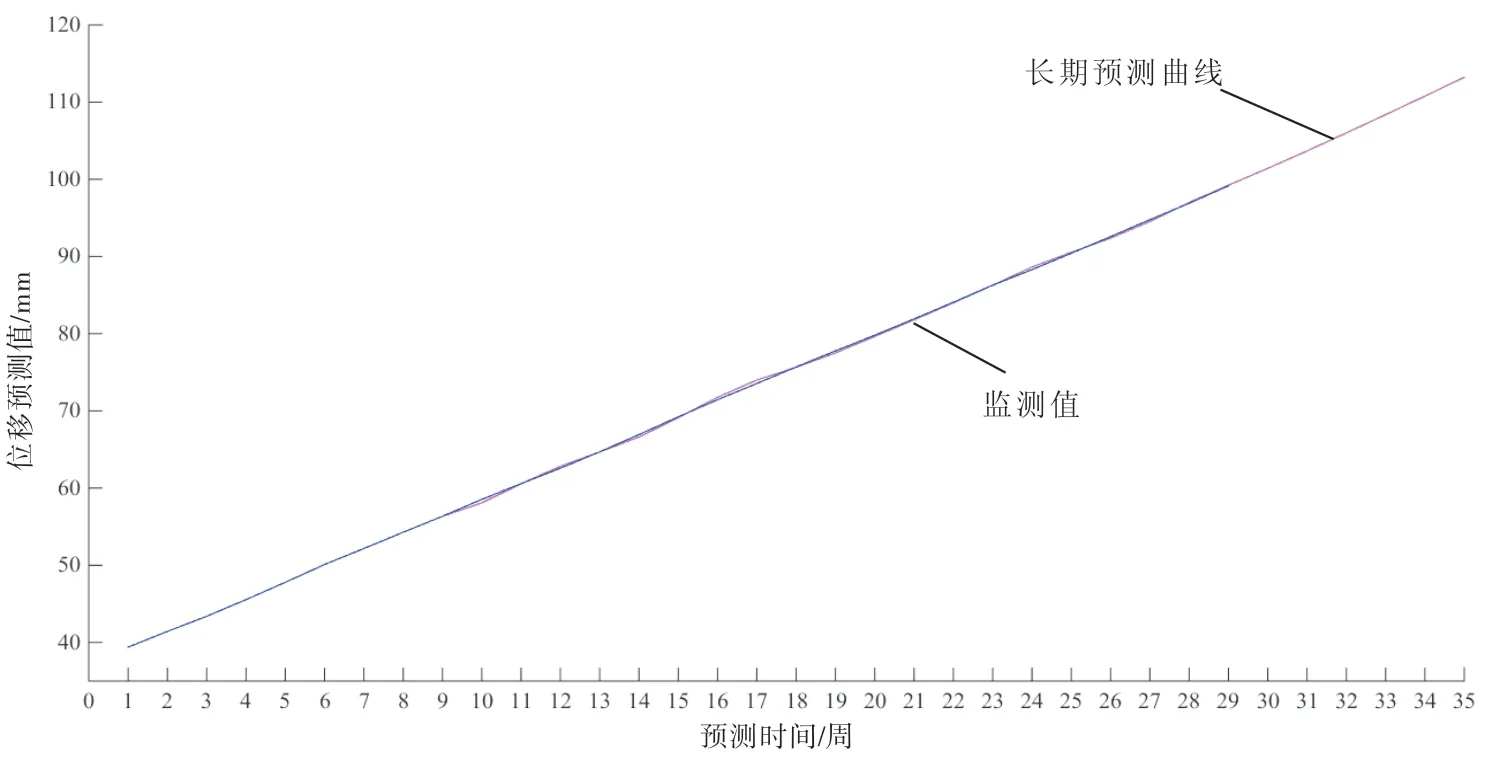
图3 JC815号监测点X向位移长期预测曲线
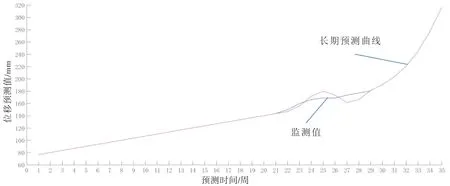
图4 JC910号监测点X向位移长期预测曲线
在无监测数据置入的情况下,图3、图4分别对JC815和JC910两处监测点做出6组预测,可以看出,优化后的灰色模型对于规律性较强的变形数据拟合精度较高,预测效果显著,变形趋势符合实际边坡位移的演化进程,可作为工程实践的参考。
3 结论
通过紫金矿排土场边坡位移预测结果分析,可以得出以下结论:
(1)传统的灰色模型对于呈指数型增长的边坡变形拟合精度较高,而实际边坡位移变形具有非线性、随机性特点,单一的指数型预测模型难以反映其变化规律,模型拟合的残差很大,而优化后的灰色模型对于线性变化、指数型增长和多项式规律的边坡变形拟合精度很高,更适合边坡的变形预测。
(2)运用滚动序列算法,能够弥补模型的不足,从而更为科学地预测边坡的变形趋势,大大提高了模型的预测精度。
(3)由于matlab软件进行数值计算时多项式最高次幂项的系数默认不为0,进行边坡变形预测时以残差值最小为约束条件适当选取预测模型的m值,并进行中长期预测,预测值具有一定的参考价值。
[1] 莫林辉,章志新,唐小富,等. 山区高速公路高边坡变形的组合预测模型研究[J]. 公路工程,2016,41(02):162-165.
[2] 孙世国,苏振华,郭珮,等. 滑坡变形组合预测方法的研究[J]. 工程地质学报,2016,24(06):1041-1047.
[3] 周英,基于改进后灰色模型的某深基坑变形预测[D].成都:成都理工大学,2015.
[4] 王朝阳,许强,范宣梅,等. 灰色新陈代谢GM(1,1)模型在滑坡变形预测中的应用[J]. 水文地质工程地质,2009,21(02):108-111.
[5] 孙世国,王超. 基于改进灰色模型的边坡位移预测[J]. 黑龙江科技大学学报,2017,27 (01):60-63.
[6] 邓聚龙. 灰色系统基本方法[M]. 武汉:华中工学院出版社,1987.
[7] 刘祖强.工程变形监测分析预报的理论与实践[M].北京:中国水利水电出版社,2008.
[8] 陈振邦,王佳欣.大数据时代下基于物联网技术的边坡监测展望[J]. 中小企业管理与科技(下旬刊),2016,18(06):158-159.
[9] 朱彦鹏,江腾,朱鋆川. 山区机场高填方边坡施工期沉降的灰色模型预测[J]. 甘肃科学学报,2016,28(1):88-92.
[10] 孙世国,杨宏,冉启发,等. 典型排土场边坡稳定性控制技术[M]. 北京:冶金工业出版社,2011.
[11] 王岩,黄张裕,张玉爽,等. 基于震荡序列的灰色预测模型在边坡沉降监测中的应用[J]. 测绘工程,2017,26(3):69-71+76.
[12] 董彦飞.边坡变形三维实体预测方法的研究[D]. 北京:北方工业大学,2016.
[13] 王豪威. 基于改进的动态灰色模型在变形监测数据分析中的应用研究[D]. 南昌:东华理工大学,2015.
DisplacementpredictionbasedonoptimizedgraymodelofdumpslopeofZijinshan
SUN Shi-guo1, WANG Chao1, ZHAO Juan2
(1.CollegeofCivilEngineering,NorthChinaUniversityofTechnology,Beijing100144,China; 2.CollegeofCivilEngineeringandArchitecture,ChinaThreeGorgesUniversity,Yichang443002,China)
2017-06-12
国家自然科学基金项目(41172250);国家重点研发计划课题(2016YFC0701810);科技创新能力建设(PXM2017-014212-000015);中冶交通建设集团科技项目(2017-SZ1);国家十二五科技支撑项目(2012BAK09B06)
孙世国(1959—),男,辽宁鞍山人,教授、博导,博士后。
1674-7046(2017)04-0001-06
10.14140/j.cnki.hncjxb.2017.04.001
TU457
A
