混凝土收缩徐变对斜拉桥叠合梁受力的影响

2017-10-13叶佳，杨伟，万阳

河南城建学院学报 2017年4期

关键词：成桥徐变斜拉桥

叶佳，杨伟，万阳

(重庆交通大学土木工程学院，重庆 400074)

混凝土收缩徐变对斜拉桥叠合梁受力的影响

叶佳，杨伟，万阳

(重庆交通大学土木工程学院，重庆 400074)

以某双塔混合梁斜拉桥为工程背景，利用Midas/Civil建立全桥空间有限元模型，分析了成桥阶段混凝土收缩徐变对斜拉桥主梁内力行为的影响。结果表明：混凝土收缩徐变效应对叠合梁正弯矩具有明显的削峰作用，且明显增加主梁负弯矩值；同时混凝土收缩徐变会引起叠合梁中钢梁与混凝土桥面板之间的应力重分布，使靠近钢-混凝土结合段处的混凝土主梁应力改变较大。

混合梁斜拉桥；钢-混叠合梁；收缩徐变

Abstract：Based on the engineering background of a twin-tower hybrid girder cable-stayed bridge, the finite element model of the whole bridge is established by using Midas/Civil, and the influence of concrete shrinkage and creep on the internal force behavior of the cable-stayed bridge is analyzed. The results show that the shrinkage and creep effect of concrete has obvious peak-shaving effect on the positive bending moment of the composite beam, and the negative moment value of the main beam is increased obviously. At the same time, the shrinkage and creep of concrete will cause the stress redistribution between the beam and the concrete slab of the composite beam, so that the stress of the main beam near the steel-concrete joint section is changed greatly.

Keywords：cable-stayed bridge; steel and concrete composite beams; creep and shrinkage

混合梁斜拉桥是指斜拉桥的主梁由两种不同的材料组成，主跨的梁体为钢材，边跨的梁体为混凝土梁材料。在大跨桥梁结构中，通常对主跨的主梁有一定的刚度要求，因此主跨主梁采用钢-混叠合梁形式，则形成含有钢-混叠合梁段的混合梁斜拉桥。

对于斜拉桥，拉索的水平分力会使混凝土的徐变增加，引起组合截面上的钢梁与混凝土桥面板之间发生应力重分布，从而导致结构的变形增加及叠合梁中钢梁和混凝土桥面板应力的变化[1]。因此，在对含钢-混叠合梁段混合梁斜拉桥结构的分析中应充分重视混凝土收缩徐变效应的影响，找出主梁在收缩徐变效应下内力的变化规律和变化趋势，以保证该类斜拉桥的结构安全和正常使用[2]。

近年来，国内外一些学者对钢-混叠合梁结构的收缩徐变效应进行了广泛研究[3-4]，但对含有钢-混叠合梁段的混合梁斜拉桥受混凝土收缩徐变影响的研究还不多见。本文在总结钢-混叠合梁收缩徐变计算理论的基础上，以某双塔混合梁斜拉桥为工程背景，通过有限元建模分析，对含有钢-混叠合梁段的混合梁斜拉桥收缩徐变效应进行了研究，以对同类桥梁设计及施工提供参考。

1 混凝土收缩徐变理论

20世纪30年代F.Dischingre提出了由混凝土徐变、收缩导致的混凝土与钢筋截面应力重分布与结构内力重分配计算的微分方程解。这种微分求解方法基于较多假定，与实际情况偏差较大，同时对于多次超静定结构采用微分法求解过程十分复杂。1967年，H.Trost教授引入老化系数概念，提出由徐变导致的应力与应变之间关系的代数方程表达式，不仅简化了计算而且提高了精度。随着计算机技术的进步和有限元分析方法的应用，Trost-Bazant将按龄期的有效模量法与有限元法相结合，使得混凝土的徐变、收缩计算能够采用更逼近实际的有限单元、逐步计算法[5]。

由于斜拉桥通常采用悬臂施工，工期较长，且混凝土加载龄期差异较大，因此常采用逐步分析法[6-7]计算其收缩、徐变效应。设ti为计算时刻，将应力-应变增量的关系表达为：

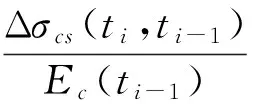
(1)

式中：Δεcs(ti，ti-1)、Δσcs(ti，ti-1)为ti-1至ti时间内由徐变与收缩引起的应变增量和应力增量；Δσ(ti)为时刻ti的应力增量；Δεs(ti，ti-1) 为ti-1至ti时间内发生的收缩应变增量；E(tj)为时刻tj的弹性模量。

同理，截面曲率增量与弯矩增量的关系为：

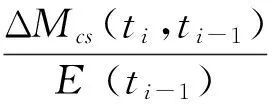
(2)

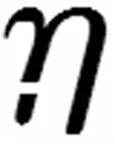
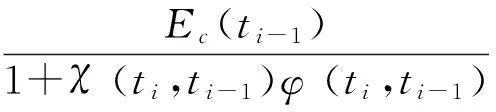
(3)

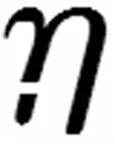
(4)

设轴向力增量ΔNcs(ti，ti-1)=Δσcs(ti，ti-1)Ac，将式(3)、(4)带入式(1)，轴向力增量可表示为：

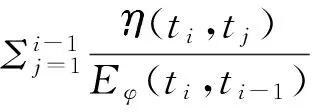
(5)

同理，将式(3)、(4)带入式(2)，弯矩增量可表示为：

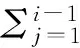
(6)

根据有限单元法形成荷载矩阵的原理，对结构中任一平面梁单元施加约束，使其在第i个时间间隔内节点位移增量为0，则由节点约束产生的轴向力增量与弯矩增量分别为：

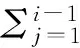
(7)

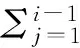
(8)

2 算例分析

2.1工程概况

某双塔混合梁斜拉桥，主桥结构为双塔、双索面、密索体系斜拉桥，主梁为纵向半漂浮体系，主跨跨径为572 m，两岸边跨跨径分别为280 m和198 m，北岸为辅助通航孔区，南岸不受通航影响。因此南岸边跨布置三个辅助墩，主桥全长1 050 m，该桥总体布置如图1所示。该桥主跨及北岸边跨主梁采用双纵肋叠合梁，钢主梁为工字形断面，叠合梁中心梁高3.5 m。叠合梁主横隔板标准间距为13.5 m，主横隔板间设置次横隔板，间距为4.5 m。南岸边跨主梁采用双纵肋混凝土主梁，中心梁高3.5 m。叠合梁和混凝土主梁结合部采用钢-混凝土过渡段连接，结合部位于中跨侧距离南岸索塔10.725 m处。混凝土主梁采用C60等级的混凝土，钢梁采用Q370qD结构钢。

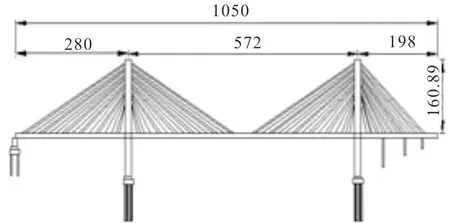
图1 主桥总体布置图(单位:m)

2.2有限元模型

采用有限元软件Midas/Civil建立全桥空间有限元模型，主梁采用梁单元模拟，斜拉索采用索单元模拟，叠合梁采用施工阶段联合截面法模拟[4]；混凝土材料的收缩徐变系数曲线以10 000 d为终值。通过建立上下两个节点，节点之间采用弹性连接的形式模拟支座，弹性连接刚度按支座的实际刚度输入。全桥共划分为311个单元，其中叠合梁249个单元，混凝土梁62个单元，如表1所示。全桥有限元结构模型如图2所示。

表1 全桥有限元模型主梁分布

图2 全桥空间有限元模型

3 有限元分析结果

3.1对主梁内力的影响

本文混凝土收缩量及徐变系数的计算采用了 CEB-FIP90的计算模型。根据全桥有限元模型的计算结果，主梁在成桥初期和成桥后期10 000 d两个时间点的轴力、弯矩、剪力分别如表2及图3、图4所示。

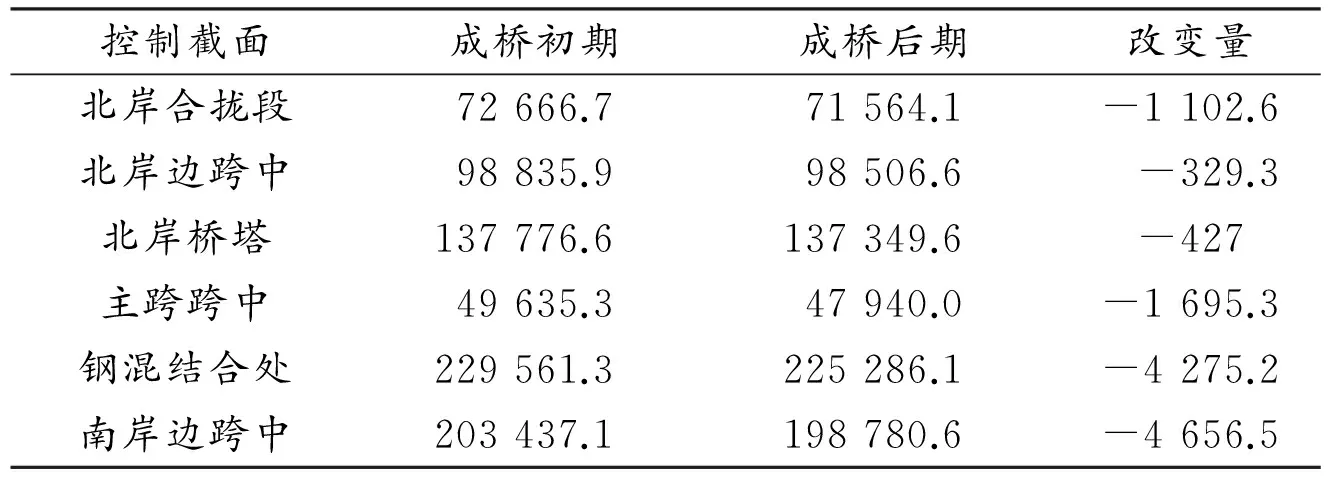
表2 混凝土收缩徐变前、后主梁轴力 kN

由表2可知：主梁最大轴力发生在南岸桥塔处，其轴力值为229 561.3 kN。成桥阶段混凝土收缩徐变对主梁的轴力值影响较小，对叠合梁段的影响相对更小。

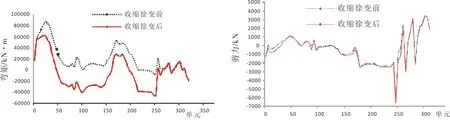
图3成桥阶段收缩徐变前、后主梁弯矩值图4成桥阶段收缩徐变前、后主梁剪力值

由图3可知：成桥阶段混凝土收缩徐变对混凝土梁弯矩的影响相对较小，而对叠合梁的弯矩有较大影响。叠合梁的最大正弯矩发生在北岸交界墩处，混凝土收缩徐变发生后，其弯矩值符号发生改变且产生较大的负弯矩，最大负弯矩值为-45 785.7 kN·m，正弯矩峰值减幅达到33.9%，也就是说混凝土收缩徐变效应对叠合主梁产生了内力重分布，因而对正弯矩具有削峰的作用。

由图4可知：成桥阶段混凝土收缩徐变对主梁剪力值影响较小。成桥阶段最大剪力值为6 609 kN，混凝土收缩徐变完成后最大剪力值为6 503 kN，主梁的最大剪力值均发生在南岸桥塔钢-混凝土结合段处。

3.2叠合梁应力分析

叠合梁中钢主梁与混凝土桥面板在成桥阶段混凝土收缩徐变前后应力变化情况如图5、图6所示。

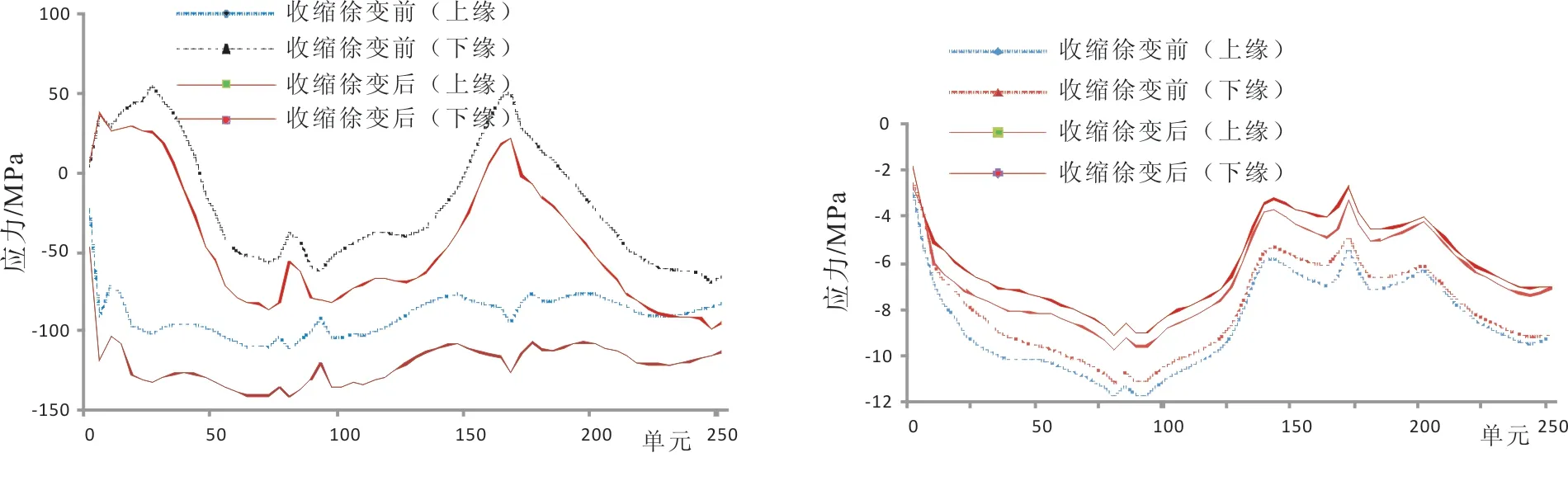
图5成桥阶段收缩徐变前、后钢梁应力值图6成桥阶段收缩徐变前、后桥面板应力值

由图5、图6可知：成桥阶段混凝土的收缩徐变效应并未造成混凝土桥面板出现拉应力，混凝土桥面板的最大压应力均出现在北岸桥塔处；在主跨跨中以及北岸边跨交界墩处，钢主梁下缘出现拉应力，拉应力数值较小。混凝土收缩徐变前后，钢主梁的上下翼缘的压应力均有所增加，北岸边跨跨中处钢梁下缘压应力由-14.1 MPa变为-46.9 MPa，增幅达到232.6%，；而混凝土桥面板的压应力均减小，最大减幅为29.4%，位于主跨跨中。由此可知：在混凝土的收缩徐变作用下，叠合梁截面发生了应力重分布。

3.3混凝土主梁应力分析

混凝土主梁在成桥阶段混凝土收缩徐变前后应力变化情况如图7所示。

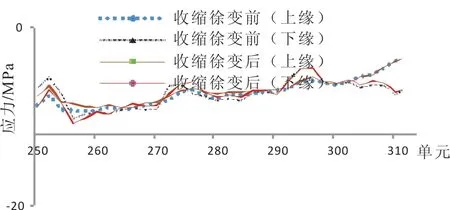
图7 成桥阶段混凝土主梁收缩徐变前后应力值

由图7可知：成桥阶段混凝土的收缩徐变效应使混凝土主梁的上翼缘应力有所降低，对靠近钢-混凝土结合段处的主梁影响比较大，最大降幅13.2%；在靠近钢-混凝土结合段处的混凝土主梁下翼缘应力增加，最大增幅32.5%，其余位置均有所降低，混凝土收缩徐变效应对南岸辅助墩位置处混凝土主梁下翼缘应力没有明显的影响。

4 结论

成桥阶段混凝土收缩徐变效应对该斜拉桥主梁的受力状态有较大的影响，具体影响规律如下：

(1)混凝土后期收缩徐变对主梁的轴力、剪力影响均较小，但对主梁弯矩的影响较大，其对钢-混组合梁弯矩的影响程度大于对混凝土主梁弯矩的影响程度。

(2)混凝土后期收缩徐变会造成钢主梁与混凝土桥面板之间发生内力重分配，进而使钢主梁应力大幅增加，混凝土桥面板应力减小；钢主梁应力最大增幅为232.6%，桥面板应力最大减幅为29.4%。因此，设计中应重视混凝土收缩徐变效应使钢主梁压应力增加后引起的腹板及下翼缘的稳定问题。

(3)靠近钢-混凝土结合段处混凝土主梁的下翼缘应力增加，最大增幅32.5%，在辅助墩处混凝土主梁下翼缘应力改变量较小；上翼缘应力均有所降低，靠近钢-混凝土结合段处最大减幅为13.2%。

通过对比分析，在成桥阶段混凝土的收缩徐变效应对该斜拉桥主梁内力的影响规律可得：混凝土后期收缩徐变效应对混凝土主梁受力的影响相对较小，对叠合梁主梁受力影响较大。相关研究结论可为同类桥梁的设计、施工及成桥后的研究分析提供重要的参考，设计和施工中应采取相应措施减少混凝土的后期收缩徐变，保证该斜拉桥的结构安全和正常使用。

[1] 熊礼鹏，吴冲，陆春阳.钢-混凝土箱型组合斜拉桥主梁混凝土收缩徐变分析[J].交通科技，2010(4):1-3.

[2] 李小锋，宋景涛. 收缩徐变效应对混凝土斜拉桥内力状态影响分析[J]．上海公路, 2015(3): 40-42.

[3] 邱文亮，姜蒙，张哲. 钢—混凝土组合梁收缩徐变分析的有限元方法[J]. 工程力学，2004, 21(4): 162-166.

[4] 李法雄，王晓夫，黄晓卿，等. 钢-混凝土组合梁斜拉桥收缩徐变影响[J].公路交通科技，2013,30(10):54-60.

[5] 项海帆. 高等桥梁结构理论[M].北京：人民交通出版社，2001.

[6] 郑军. 混凝土收缩徐变对斜拉桥受力性能的影响[J]. 太原科技大学学报，2013, 39 (1): 174-176 .

[7] 陈亮，邵长宇. 结合梁斜拉桥混凝土收缩徐变影响规律[J].桥梁建设，2015 (1): 74-78.

Effectofshrinkageandcreepofconcreteonstressofcompositebeamofcable-stayedbridge

YE Jia, YANG Wei, WAN Yang

(DepartmentofCivilEngineering，ChongqingJiaotongUniversity，Chongqing40000，China)

2017-06-07

重庆交通大学研究生教育创新基金(20160112)