基于LM-BP神经网络的高层建筑物沉降变形预测

高 宁,吴秋堂,王静燕

(1. 河南城建学院 测绘与城市空间信息学院，河南 平顶山 467036；2. 东华理工大学 江西省数字国土重点实验室，江西 南昌 330013；3. 江西省基础测绘院，江西 南昌 330013；4.石家庄信息工程职业学院 通信工程系，河北 石家庄 050035)

基于LM-BP神经网络的高层建筑物沉降变形预测

高 宁1, 2,吴秋堂3,王静燕4

(1. 河南城建学院 测绘与城市空间信息学院，河南 平顶山 467036；2. 东华理工大学 江西省数字国土重点实验室，江西 南昌 330013；3. 江西省基础测绘院，江西 南昌 330013；4.石家庄信息工程职业学院 通信工程系，河北 石家庄 050035)

以高层建筑物沉降变形预测为主要研究目的，比较BP神经网络在不同学习规则下对预测精度的影响，针对LM-BP (Levenberg-Marquardt)算法，深入讨论LM-BP建模时应注意的若干问题，给出了其网络结构参数优化实施的具体流程，构建LM-BP高层建筑物沉降变形位移预测的最优网络拓扑结构。应用结果表明，基于LM算法的BP神经网络应用于变形预测中能获得较高的预测精度。

高层建筑物；沉降变形； LM算法；BP算法；预测

Abstract：Based on the prediction of settlement deformation of high-rise buildings, the influence of BP neural network on prediction accuracy is compared, in view of the LM-BP (Levenberg-marquardt) algorithm, this paper discusses some problems that should be paid attention to in LM-BP modeling, gives the concrete flow of its network structure parameter optimization, and constructs the optimal network topological structure for the prediction of settlement deformation displacement of LM-BP high-rise buildings. The application results show that the BP neural network based on LM algorithm can obtain high prediction precision in deformation prediction.

Keywords：high-rise building; subsidence and deformation; LM algorithm; BP algorithm; prediction

近年来，随着我国城市化进程日益加快，越来越多的建筑物朝着高层、超高层方向发展。高层建筑物在施工期间，由于主体荷载的不断增加，在地基基础和上部结构的共同作用下，建筑物主体将会发生沉降变形，当沉降变形为均匀沉降时，通常只对建筑物的使用带来一定的影响，并不会对建筑物的主体结构造成破坏。但当不均匀沉降发生时，且差异沉降量超过其允许值时，将直接破坏建筑物的主体结构，从而影响建筑物的安全。因此，定期对高层建筑、大型工业建筑、重要构筑物等进行变形监测，掌握其变形规律，对其未来变形趋势的准确预测具有重要的意义[1-4]。

由于建筑物沉降变形的诱发因素、形成条件及演化过程具有复杂性及多样性，使得建筑物沉降变形的力学特征和形变趋势表现出确定性与随机性并存的非线性特征。因此，其变形过程不能用准确的数学模型表达出来，给变形分析和预测带了很大困难。目前，对建筑物沉降变形预测采用较多的方法是利用形变位移监测时间序列，建立各类时序分析模型，对其变形过程进行模拟及预测。事实上，现有的多数预测理论模型均建立在参数模型基础之上，在实践应用中，存在模型参数物理意义不明确、有效监测信息利用不充分等特点[2-6]，为了避免上述缺点，BP(back propagation,bp)人工神经网络方法逐渐应用于各种建筑物的变形预测中，取得了较好的预测效果，如马丽霞等利用BP神经网络建立了大坝变形的区间预报模型[6]；潘国荣等针对BP算法存在的固有缺陷，提出了新的收敛条件、优化激励函数的改进网络，将其成功应用于某超高烟囱的沉降变形预测中[7]；祁长青利用改进的BP神经网络建立了冻土区路基变形的非线性模型，得出了温度对路基变形的影响规律[8]。

众多研究结果表明：影响神经网络预测精度的主要因素是网络学习规则及网络拓扑结构。然而，已有BP神经网络进行变形分析与预报的文献中，主要是以标准的BP网络为基础，讨论网络拓扑结构的优化问题，对BP网络学习规则如何影响预测精度的研究尚不多见。随着对BP网络研究的深入，相关研究人员在标准BP算法基础上，提出了新的学习规则下的BP算法，如LM(levenberg-marquardt)算法、变梯度算法、动量算法、牛顿算法等。本文以BP算法的学习规则为出发点，研究BP学习规则对变形预测结果的影响，同时讨论最优网络拓扑结构的建立。

1 沉降变形预测中BP网络学习算法比较

1.1 BP网络学习算法比较

BP算法的学习过程是基于梯度下降算法来实现对网络权值和阈值的修正，从而达到网络学习误差平方和最小，其训练过程由信息正向传播和误差反向传播两部分组成：

(1)正向传播过程中，输入信息从输入层经隐含层逐层处理，进而传向输出层，每一层神经元的输出作用只影响下一层神经元的状态；

(2)误差反向传播，如果在输出层不能得到期望输出，网络转向反向传播过程，将误差信号沿原来的连接通路返回，通过修改各层神经元的权值和阈值，直到达到期望输出。

已有研究成果表明标准BP算法存在着许多缺陷：如网络学习效率低、易形成局部极小、网络学习时间长、收敛速度慢等等，从而影响了预测的精度[9-10]。为此，在标准BP算法的基础上，相关研究人员进行了许多改进，改进措施主要有两类:

(1)基于标准数值优化的改进算法，如LM (Levenberg-Marquardt)算法、牛顿法、变梯度法等；

(2)基于标准梯度下降的改进方法，如动量的BP算法、自适应学习率调整法等。

不同学习规则下BP网络特点比较见表1。

表1 BP网络不同学习规则下网络特点比较[6-10]

1.2不同学习算法下BP网络收敛效率比较

由表1可知，BP网络在不同的学习规则下，网络的学习速率、收敛速度、迭代计算次数等方面存在较大差异。对于建筑物的沉降变形预测来讲，在何种学习规则下，BP网络的预测效果达到最优，为此，有必要讨论不同学习算法下BP网络对预测精度的影响。

在进行比较计算过程中，设定如下前提条件：

(1)构建BP网络时，选取相同的建模样本和检验样本；

(2)构建BP网络均为三层网络，各层网络的节点数相同；

(3)网络学习速率均为经验值0.05；

在上述前提约束条件下，利用文献[11]中某高层建筑物的36期沉降变形进行建模预测比较。其中1-30期数据作为训练样本，用来对网络进行训练，31-36期数据作为检验样本，来检验网络的泛化能力。对表1中不同学习规则下的BP算法进行建模。网络学习迭代次数及网络训练、预测精度见表2。

表2 不同学习规则下BP网络收敛效率比较

由表2统计结果可以看出：变梯度算法、拟牛顿算法、LM算法三种学习规则下网络学习速率较快，经过几次迭代计算，网络即可收敛，达到期望输出；LM算法收敛速度最快，其网络学习性能曲线如图1所示。

标准BP算法和动量BP算法网络学习速度较慢，经过近千次迭代计算，网络才达到收敛精度；在相同的期望输出下，以上5种BP算法均能达到收敛精度，从网络训练样本和检验样本均方差中，可以看出无论是模拟精度还是预测精度，LM算法预测精度最高，网络泛化能力最好。

图1 LM-BP算法网络学习性能曲线图2隐含层的节点数与网络预测误差关系

2 LM-BP最优网络拓扑结构的建立

通过比较计算，发现LM-BP网络的收敛效率及预测精度方面均优于其他学习规则。在LM算法下，如何建立最优网络拓扑结构则是需要讨论的另一关键性问题。

2.1隐含层节点数的确定

由Kolmogorov定理可知，一个三层的前向网络足以完成任意的维到维的映射，即选用一个隐层的BP网络便可以满足任意非线性目标函数逼近的要求[9]。因此，LM算法下网络结构设置为3层，一个输入层、一个隐含层和一个输出层。网络结构确定后，下面讨论网络参数的选取问题(比较计算数据选取同1.2节)。

由图2可知：隐含层节点数为3～15时均能满足实验要求，随着节点数的增加，网络训练误差呈现先减小后增加的趋势，隐含层节点为13时，BP网络拟合效果最好。建议在利用BP神经网络进行形变预测时，隐含层的节点数应根据变形数据的特点，在经验公式的指导下，经多次实验的方法确定。

2.2网络传递函数对预测误差的影响

在BP神经网络中，输入层、隐含层、输出层间学习训练都依赖传递函数，常用的网络传递函数有[10]：Hardlim型(阈值型传递函数)、Purelin型(线性传递函数)、S型传递函数(包括对数Logsig和正切Tansig两种)，其公式表达为(函数图形见图3)：

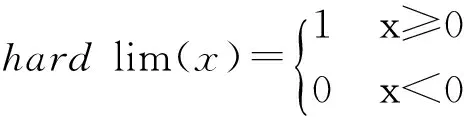
(1)

purelin(x)=x

(2)

logsig(x)=1/(1+exp(-x))

(3)

tansig(x)=2/(1+exp(-2*x))-1

(4)

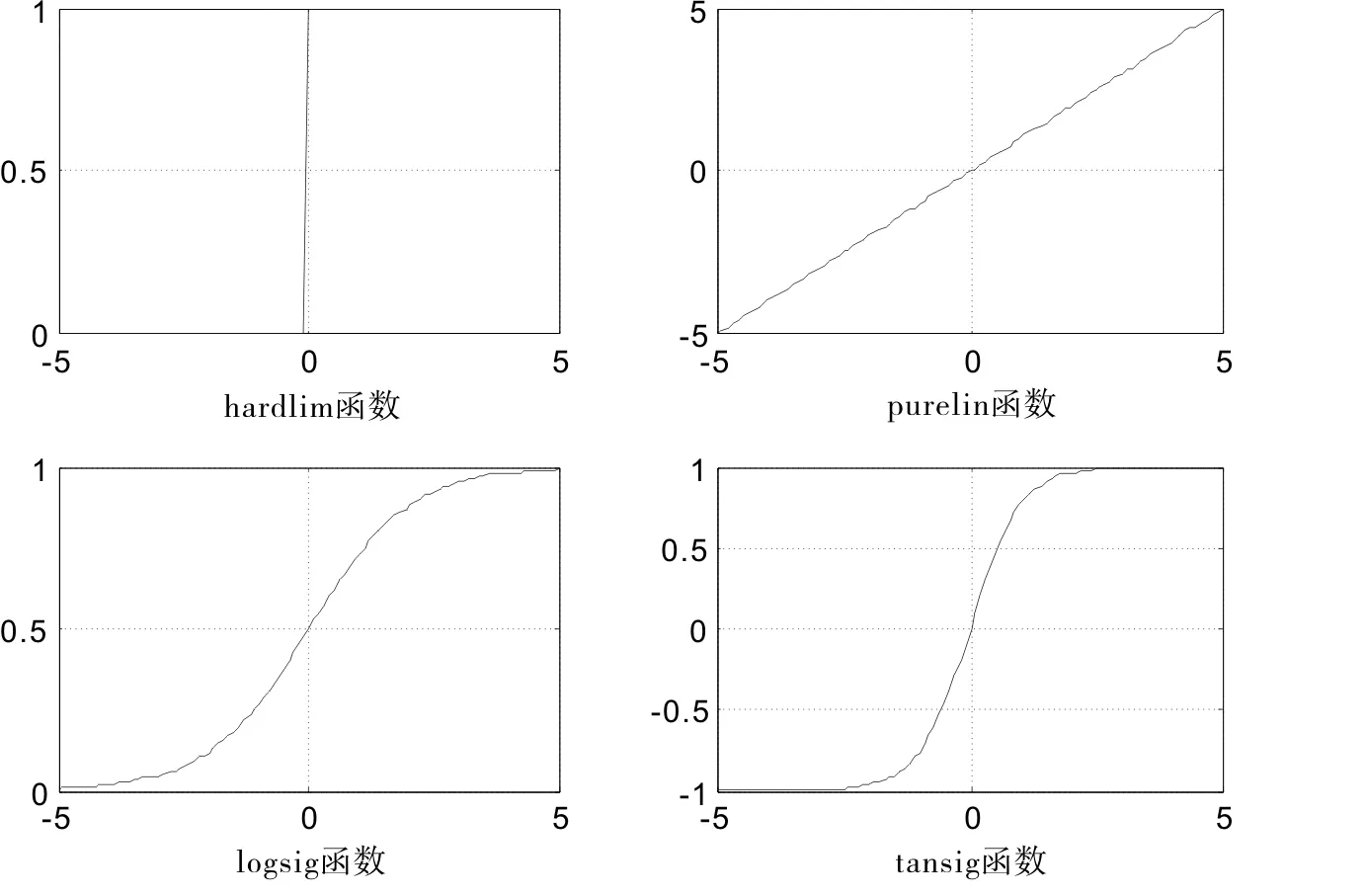
图3 BP神经网络传递函数图

用于预测时，常用的网络传递函数有logsig型、tansig型及purelin型，为了研究传递函数对预测结果的影响，将不同的传递函数互相搭配，求出网络对检验样本的预测均方误差，具体结果见表3。

表3 网络传递函数对预测结果影响比较

由表3可知：隐含层函数选取logsig，输出层函数选取purelin为最优组合，当隐含层函数选取纯线性函数purelin时，组合任意的输出层函数，网络均不收敛，主要因为沉降变形监测数据受到各种不确定因素影响，表现为高度的非线性相关，隐含层采用纯线性函数很难达到预期要求。

2.3学习速率的选取

学习速率的选取决定网络每次循环训练中所产生的权值变化量，学习速率太大，则导致系统不稳定，学习速率太小，导致网络训练时间过长，不能保证网络误差最终趋于最小值。

对于学习速率的选取，目前并没有确定的方法，只能依靠经验值来确定。计算过程中，采用迭代计算的方法来确定，在经验值0.01～0.8范围内，以0.01为步长进行迭代计算，统计网络训练样本的均方差，具体计算结果见图4。

由图4可以看出：学习速率直接影响网络训练的稳定性，网络学习速率越大，网络波动性也越大，经多次迭代计算，当学习速率为0.05时，网络稳定性最好。

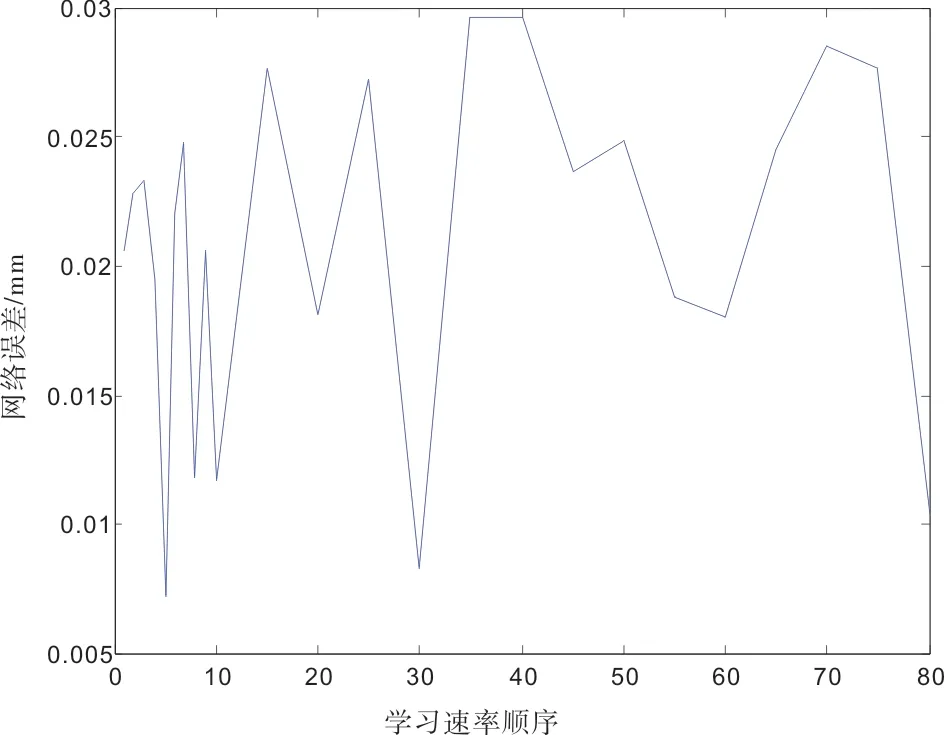
图4 学习速率对网络训练的影响

3 LM-BP网络预测效果比较

在LM算法下，建立最优的网络拓扑结构：单隐含层，隐含层节点数为13；隐含层转换函数为logsig，输出层转换函数为purelin，训练函数为trainlm，学习速率为0.05，网络误差为0.3 mm。为了比较预测效果，计算过程中，同时建立了时序AR模型，与LM算法下的BP网络预测效果进行比较。

建模样本选取1～30期沉降变形数据，对31～36期观测数据进行预测，两者预测结果见表4。LM算法BP网络和AR模型预测结果的均方误差MSE分别为0.083 7、0.444 8。

表4 LM算法BP网络和AR模型预测结果比较 mm

由表4可以看出：LM算法下BP神经网络进行变形预测，具有较好的预测效果，且预测精度高于自回归AR模型。

4 结论

(1)不同学习规则下的BP神经网络在学习训练中具有不同的特点，在利用BP神经网络进行建模预测时，应根据预测问题的实际情况，选取合适的学习规则建立网络；

(2)利用BP神经网络进行变形预测时，存在一个最优网络问题，最优网络的确定需在确定BP学习规则基础上，对影响网络预测结果的参数进行优选；

(3)基于LM算法的BP神经网络，只要建立合理的网络拓扑结构，可以取得较高的预测精度。

[1] 侯建国，王腾军.变形监测理论与应用[M].北京：测绘出版社，2008.

[2] 赵仲荣，袁树才，张立群.建筑物差异沉降的时间序列分析与预报[J].工程勘察，2010，38(1)：73-75.

[3] 孙永荣，胡应东，陈武，等.基于GM(1,1)改进模型的建筑物沉降预测[J].南京航空航天大学学报，2009，41(1)：107-110.

[4] 高宁，崔希民，高彩云.高层建筑物沉降变形的灰线性预测[J].测绘科学，2012，37(3)：96-98.

[5] 王威，苏经宇，侯本伟，等.建筑物非线性变形动态预测的数据机理:自记忆模型[J].科学通报，2012，57(23)：2171-2176.

[6] 马丽霞，王凤艳，王静.基于Matlab工具箱的神经网络在大坝变形区间预报中的应用[J].测绘通报，2010(5)：35-37.

[7] 潘国荣，谷川.BP算法改进及其在变形数据处理中的应用[J].同济大学学报(自然科学版)，2008，36(1)：118-121.

[8] 祁长青，吴青柏，施斌，等.BP神经网络在冻土路基变形预测中的应用[J].水文地质工程地质，2007，34(4)：27-30.

[9] 高彩云，崔希民.露天矿高陡边坡变形预报的最优LMBP算法研究[J].煤炭技术，2015，34(9)：189-191.

[10] 高彩云. 基于智能算法的滑坡位移预测与危险性评价研究[D].北京：中国矿业大学(北京)，2016.

[11] 王新洲，陶本藻，邱卫宁，等.高等测量平差[M].北京：测绘出版社,2006.

PredictionofsubsidenceanddeformationofhighrisebuildingbasedonLM-BPneuralnetwork

GAO Ning1,2, WU Qiu-tang3, WANG Jing-yan4

(1.SchoolofGeomatics&UrbanInformation,HenanUniversityofUrbanConstruction,Pingdingshan467036,China; 2.JiangxiProvincialKeyLabforDigitalLand,EastChinaInstituteofTechnology,Nanchang330013,China;3.BasicSurveyingandMappingInstituteofJiangxiProvince,Nanchang330013,China; 4.Information&CommunicationEngineering,ShijiazhuangInformationEngineeringVocationalCollege,Shijiazhuang050035,China)

2017-06-19

江西省数字国土重点实验室开放研究基金资助项目(DLLJ201508，DLLJ201710)；河南省高等学校重点科研项目(16A420001，18A420002)；河南城建学院青年骨干教师资助项目；河南城建学院学术技术带头人资助项目(YCJXSJSDTR201704)

高 宁(1982—)，男，河北保定人，博士，副教授。

1674-7046(2017)04-0007-06

10.14140/j.cnki.hncjxb.2017.04.002

TU362

A