基于神经网络和遗传算法的系泊优化设计

许小颖，周盼，王宽

1文华学院机械与电气工程学部，湖北武汉430074

2中国船级社武汉分社，湖北武汉430074

基于神经网络和遗传算法的系泊优化设计

许小颖1，周盼1，王宽2

1文华学院机械与电气工程学部，湖北武汉430074

2中国船级社武汉分社，湖北武汉430074

［目的］为使船舶维持作业位置的稳定，需采用系泊系统来减小浮体的平动。［方法］以一艘南海作业的铺管船为例，通过优化锚泊线的布置方式来最大限度地减小系泊状态下锚链的平动位移量，保障船舶作业安全。首先，以抛锚距离和锚链方位角作为正交试验的因素，得到不同的系泊布置方案，利用Moses软件计算不同布置方案在不同浪向下的时域运动位移和锚链受力情况。然后，将结果作为样本，对BP神经网络进行训练，实现BP网络对Moses时域计算的仿真。最后，将抛锚距离和锚链方位角作为优化变量，取不同浪向下的加权平动位移为优化目标，并以BP神经网络的泛化能力代替Moses的时域计算，采用遗传算法进行优化求解。［结果］结果表明，该铺管船各个浪向下的平动位移均有了显著的减小，优化效果明显，［结论］可为海上浮式结构物的系泊布置提供参考。

系泊优化；BP神经网络；遗传算法；Moses；时域分析

Abstract：［Objectives］In order to maintain the stability of the position of a ship,a mooring system is required to reduce the translational motion of floating structures.［Methods］Taking a pipe-laying vessel in the South China Sea as an example,it is possible to minimize the translational displacement of the anchor chain in the mooring state by optimizing the arrangement of the anchor line to ensure the safe operation of the ship.First,we can obtain several different layouts through orthogonal testing after selecting the azimuth and distance of the anchor chain as the test factors.We then calculate the different movements and force in time domain value at different wave direction angles for each layout using Moses.With the calculation results as samples,the BP neural network method achieves time domain simulation in Moses.After choosing the azimuth and distance of the anchor chain as the optimization variables,and with each wave-weighted translational displacement probability as the optimization objective,we find that the generalization capability of the BP neural network method can replace the time domain calculation of Moses.［Results］Using a genetic algorithm optimization solution,movement is significantly reduced at different wave direction angles.［Conclusions］This conclusion can provide a reference for the mooring arrangements of floating structures.

Key words：mooring optimization；BP neural network；genetic algorithm；Moses；time domain analysis

0 引 言

众所周知，船舶或浮动平台要在海上保持一个固定位置，必须采用系泊系统。系泊结构运动位移过大会影响其正常作业，而锚泊线布置不合理则容易致其断裂。因此，减小系泊状态下的平动位移，合理布置锚泊线就显得尤为重要。余龙和谭家华［1］提出多目标函数的多成分锚泊线优化模型，通过遗传算法并结合图谱设计的方式，完成了锚泊系统设计实例。马小剑等［2］对风、流作用下码头的系泊船舶，以及其锚链张力和平移运动量进行了研究。Ali和Inoue［3］则假定每一根系泊缆完全相同，采用遗传算法，以横荡和纵荡的合运动最小值为目标函数，对锚链与船艏的相对夹角及锚链长度进行了优化。严传续等［4］分析了某铺管船锚泊定位系统的结构及其受力情况，通过研究锚链悬链状态的特性，提出锚泊定位系统的二次规划优化算法，并用面向对象的VC++工具开发了锚泊定位系统软件。上述学者的研究均取得了显著成果，但也存在着一些问题：首先，对于系泊系统的研究大多还停留在对简单模型的仿真模拟阶段，未涉及实船的系泊优化问题；其次，多数研究还处于针对现有布置的锚链受力与平动位移的计算上，并不能做到对不同锚泊线布局情况下结果的预测；再次，基于水动力软件模拟计算的结果虽然较合理，但耗时巨大，并不适用于锚泊线多种布局方式的推广研究。

针对上述问题，本文将从工程实际出发，以一艘在南海工作的铺管船为研究对象，将Moses软件的计算结果作为样本，与目前流行的BP神经网络和遗传算法进行结合，考虑环境因素的影响，以锚链的方位角和锚位置作为优化变量，对其布置进行优化设计。主要研究内容包括：1）根据铺管船的图纸资料，应用Moses软件建模进行频域分析，得到其水动力系数，然后通过卷积积分转化为时域下的计算结果，考虑风、流的作用，计及船体与锚链的耦合影响，采用基于Newmark积分的时域分析方法计算常规系泊布置下的船体运动及锚链受力。2）依据正交试验原理，锚链的方位角和抛锚距离各取4个水平，得到32组系泊布置方案，通过编制批处理文件，得到32组不同布置下的浮体运动与缆绳受力值，并将其作为BP神经网络训练样本进行仿真模拟。3）以抛锚距离和锚链方位角为优化变量、以不同浪向下浮体平动位移的最小值为目标函数，采用遗传算法进行优化求解，以使该位移值显著减小，优化效果明显。研究所得结果用于为海上浮式结构物的系泊布置提供参考。

1 神经网络和遗传算法

1.1 神经网络

神经网络具有强大的逼近能力和推广作用［5］，其通过协调多种输入关系来处理复杂的非线性问题，一般由输入层、隐含层和输出层组成。隐含层的数目可自定，本研究选用3层网络［6］。各层之间通过权值相连，每层均含有多个神经元，每个神经元自带阈值，这样输入和输出之间即为映射关系，通过权（阈）值来表现，如图1所示。通常采用sigmoid型作用函数，其输出范围为0～1之间的小数，采用正切sigmoid（tansig）为隐层传递函数，采用线性purelin为输出层传递函数。训练成功的三层网络模型可用图2和式（1）来表达。图2中a1为中间层变量；a2为输出变量；w1为输入层到中间层的权值；w2为中间层到输出层的权值；b1为中间层的阈值；b2为输出层的阈值；n1为中间层神经元个数；n2为输出层神经元个数；p为输入变量。

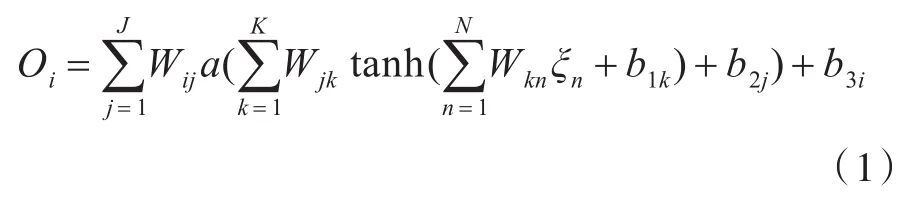
式中：Oi为输出变量；ξn为输入变量；Wkn，Wjk，Wij为各层神经元的权值；b1k，b2j，b3i为各层神经元的阈值；i，j，k分别为神经网络训练过程中输入层、中间隐层和输出层的神经元个数。

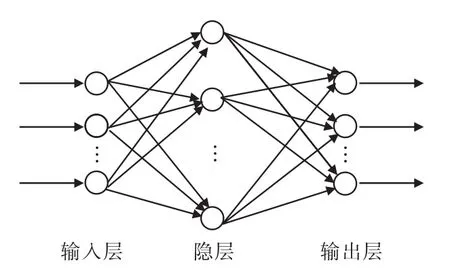
图1 BP神经网络Fig.1 Structure of BP neural network

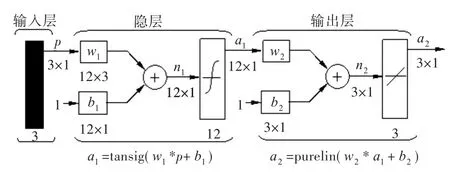
图2 BP神经网络的计算过程Fig.2 Calculational process of BP neural network

网络的误差信号［7］指的是实际输出与期望输出之间的差值，由输出端逐层向前传播。在传播过程中，网络的权值随误差反馈进行调节，经过修正后制定其相应的误差范围。本文采用的误差信号为

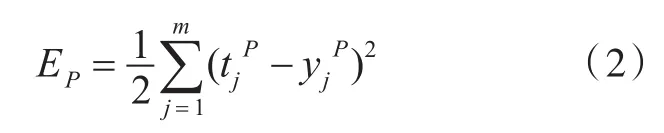
样本的输入和输出采用归一化处理，如式（3）所示。

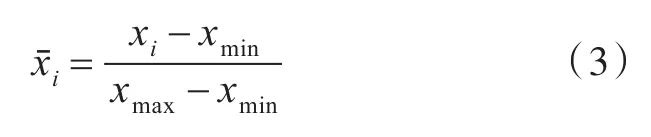
式中：xi为输入（出）数据；xmin为数据变化的最小值；xmax为数据变化的最大值。

全局误差［8］选用均方误差表示：

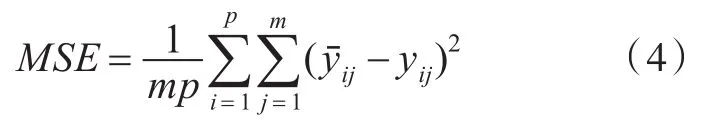
式中：m为输出节点数；p为训练样本数；为期望输出；yij为实际输出。

MATLAB软件自带的神经网络工具箱包含多种训练算法［9］，如增加动量法、自适应学习率法、弹性BP算法、L-M算法、动量及自适应学习率法等。经过试算，本文从训练时间和误差两方面考虑，选用了有动量梯度下降的BP算法训练函数，通过改进参数设置，有效避免了其收敛速度过慢、局部极值而得不到全局最优等缺点。

1.2 遗传算法

该方法的操作对象为一群二进制串，利用初始种群，选择满足适应度函数的个体，通过杂交和变异产生下代种群，直至满足期望条件，其过程如图3所示。

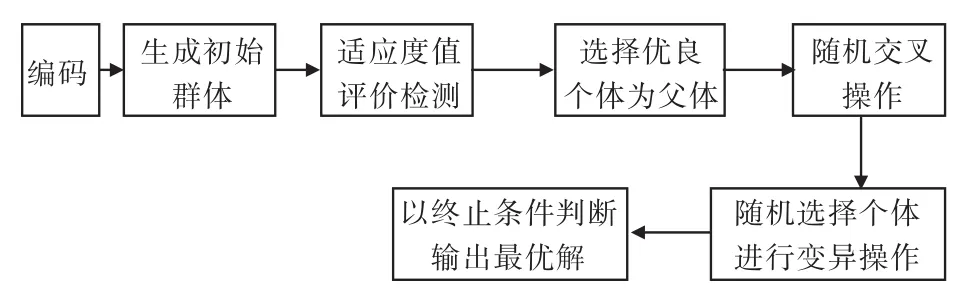
图3 遗传算法运算过程图Fig.3 Calculational process of genetic algorithm

MATLAB软件的遗传算法工具箱［10］包括各类子函数，如种群初始化函数、适应度函数、选择函数、交叉算子函数和变异算子函数。

对于种群初始化函数，选用crtrp函数，因其二进制编（解）码以及交叉、变异的实现较为方便。

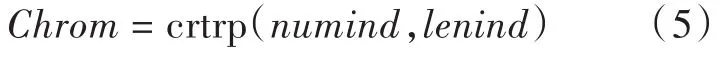
式中：numind为种群个体数；lenind为个体长度。

适应度函数主要用于评价个体优劣，适应度值越高，个体遗传下一代的概率就越高。因ranking函数是基于排序的适应度分配，支持非线性评估，故选此函数，如式（6）所示。

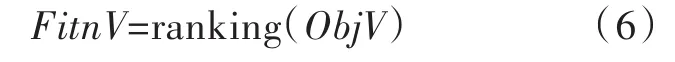
式中，ObjV值越大，分配的适应度值越小。

本文选用高级入口函数select对个体进行优胜劣汰，以方便多种群接口。

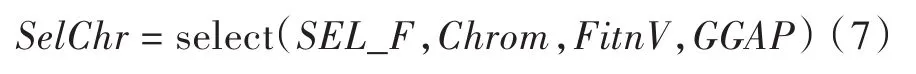
式中：SEL_F为选择函数名；Chrom代表种群；FitnV包含种群Chrom中个体的适应度值；GGAP为可选参数，指出代沟，本文取为0.9。

仅有选择操作，并不能产生新的个体，故需要有交叉操作。本文选用高级入口函数recombine，因其对所有交叉操作可提供多子群支持入口。

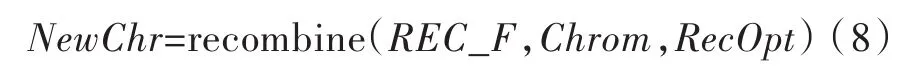
式中：REC_F为包含了低级重组函数名的字符串；RecOpt为交叉概率的可选数值，本文选用单点交叉，概率值取为0.7。

选择和交叉运算有可能会造成某些信息丢失，而变异算子函数主要用于保证算法的有效性，故采用mut函数作为变异算子。

2 算例分析

2.1 研究背景

本文以国内某公司的一艘铺管船为例，计算系泊下时域运动和锚链的受力。工作锚链采用镀锌钢丝绳，作业地点为南海某海区，船型及锚链参数、环境条件如表1所示，锚链布置情况如表2所示。其中，方位角表示锚链与船体坐标系中X轴的夹角，指向Y轴为正。

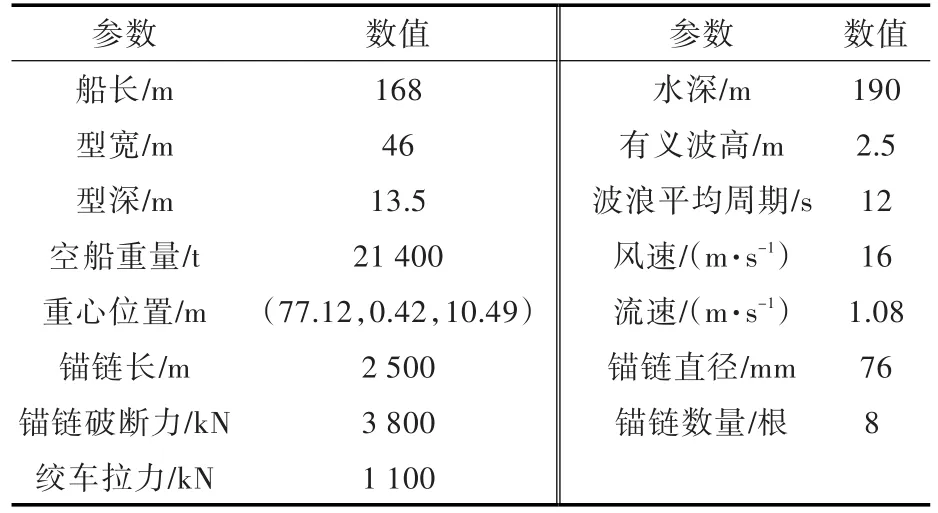
表1 船型、锚链和环境主要参数Table 1 Main parameters of ship，anchor chain and environment

初始系泊分析应用Moses软件中的时域模块［11］模拟不同位置处系泊的刚度变化，可进行横摇阻尼修正，具备一定的可信度。根据船体型线图，建立船体各站的形状，形成型表面。该船的型线较为规则，网格最大边长设为12 m，经程序自动划分后共形成678个面元。水动力模型如图4所示，整体系泊外观图如图5所示。

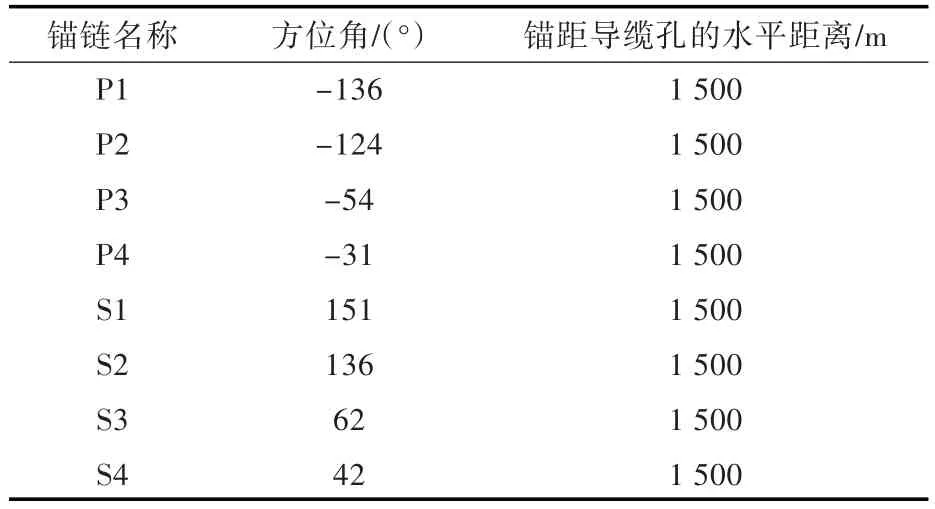
表2 锚链布置Table 2 Layout of anchor chain

图4 水动力分析模型Fig.4 Model of hydrodynamic analysis

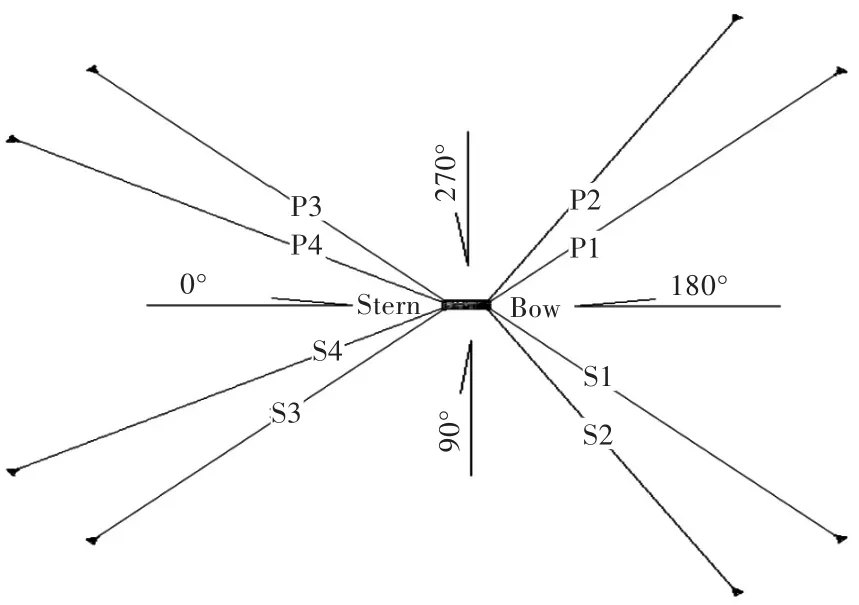
图5 系泊外观图Fig.5 Layout of mooring

通过Moses软件的频域分析模块，可得到水动力计算结果：附加质量和附加质量惯性矩系数、阻尼系数、幅值响应算子（Response Amplitude Operator，RAO）。其中，附加质量（惯性矩）系数为附加质量（惯性矩）与排水量的比值。频域计算所选的海浪谱为JONSWAP谱［8］，波浪周期范围为4～40 s，浪向角为0°，即顺浪。

对频率响应函数进行傅里叶变换可得到脉冲响应函数［12］，海况则利用JONSWAP谱形成的伪随机波来模拟，进而通过卷积积分得到时域运动响应。计算时长设为4 000 s，时间步长设为0.2 s，不计前500 s的计算结果。因系泊锚链主要影响船体（重心位置）平动，故仅列出了不同预张力下船体发生横荡和纵荡运动时的时域计算结果，如图6和表3所示，锚链受力情况如表4所示。可见在3种情况下，锚链的受力均满足强度标准，Moses软件计算结果可信。在实际工程作业中，由于锚链长度的调节可通过改变预张力来实现，故表中的30%指的是锚链预张力取为锚机工作能力的30%（30 t）［13］，其余类推。

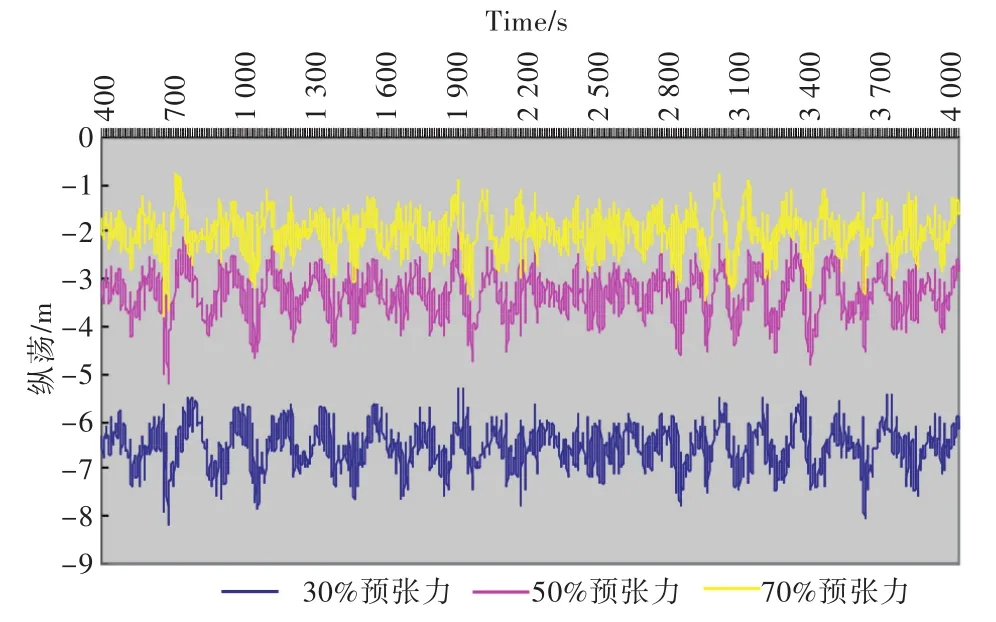
图6 不同预张力下纵荡运动Fig.6 Surge motion under different pre-tension

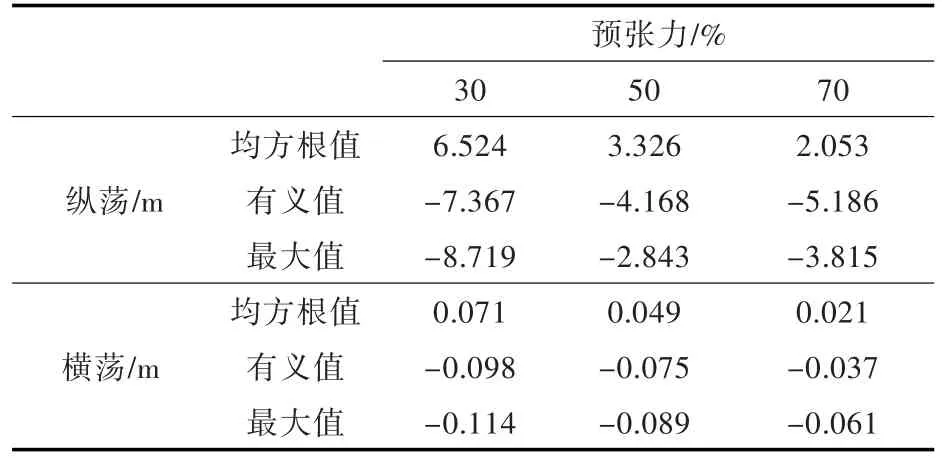
表3 不同预张力下的时域运动统计Table 3 Time-domain motion under different pre-tension

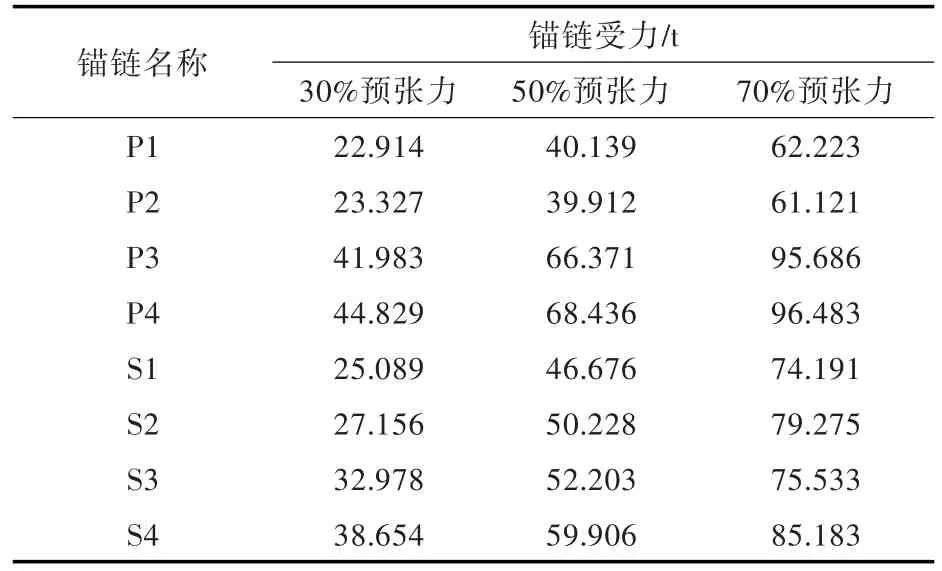
表4 锚链最大受力值Table 4 Maximum tension of anchor chain

2.2 网络计算模型

本文以锚链方位角和抛锚距离作为正交试验的因素，总个数为16。在工程实际中，因锚链多沿船长方向对称布置，故选取船右舷一侧的锚链即可，因素个数可减为8，极大地减小了工作量。对于每个因素，均取4个水平进行正交试验设计。根据工程经验，分别选取抛锚距离为850，1 000，1 500和2 000 m。为使各锚链能按逆时针方向依次排列而不交错，将锚链S2的方位角设定为95°，105°，120°和135°；锚链S4的方位角设为5°，15°，30°和45°；锚链S1和S3的方位角则根据与S2和S4的夹角来确定，其中夹角的4个水平均为10°，20°，30°，和40°。采用正交表L32（49）来安排正交试验，具体如表5所示。

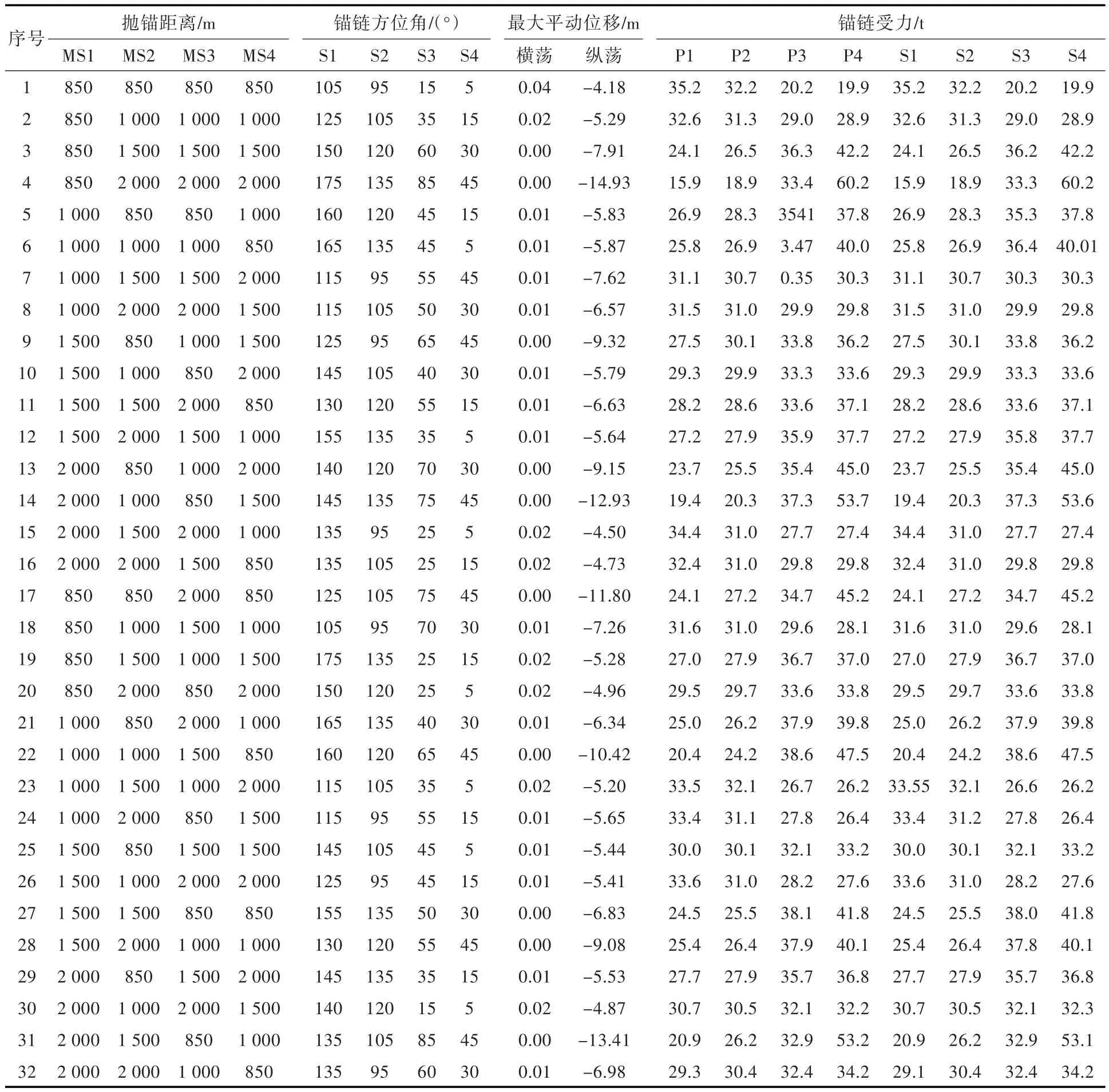
表5 0°浪向下的时域计算结果Table 5 Time domain calculation results in 0°wave direction

鉴于实验组数较多，且一组实验计算约需1 h，故编写了批处理文件，可计算得到时域下铺管船在0°，45°，90°，135°和180°浪向角下的平动位移以及锚链受力的计算结果。受篇幅所限，这里仅给出了0°浪向下的结果（表5），其余角度下的不再赘述。

根据经验，将纵荡和横荡运动仿真的输出节点设为2，锚链受力仿真的输出节点设为8，两者的输入节点均设为8；隐含节点数通过循环计算设置，从5～20中选择全局误差最小的数值作为最终节点数。将表5中的1～30组正交试验取为训练样本，31和32组正交试验取为测试样本，验证BP神经网络的泛化能力。

受篇幅所限，这里仅给出0°浪向下浮体的运动情况。由表5中横荡运动位移多接近0 m，最大值仅为0.04 m，故仅对纵荡运动进行仿真，网络训练过程如图7所示，锚链受力的BP网络训练过程如图8所示。前者经过940次训练，得到隐含节点个数为14；后者经过2 376次训练，得到隐含节点个数为14，两者的误差均小于设定的目标全局误差0.01。用第31和32组正交试验对训练好的神经网络进行测试，结果如表6所示。

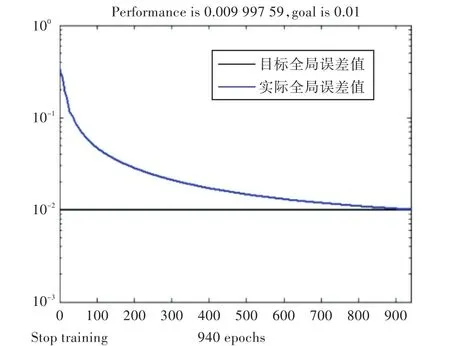
图7 0°浪向下纵荡运动仿真的网络训练过程Fig.7 Training procedure of surge motion in 0°wave direction

图8 0°浪向下锚链受力的网络训练过程Fig.8 Training procedure of anchor chain tension in 0°wave direction

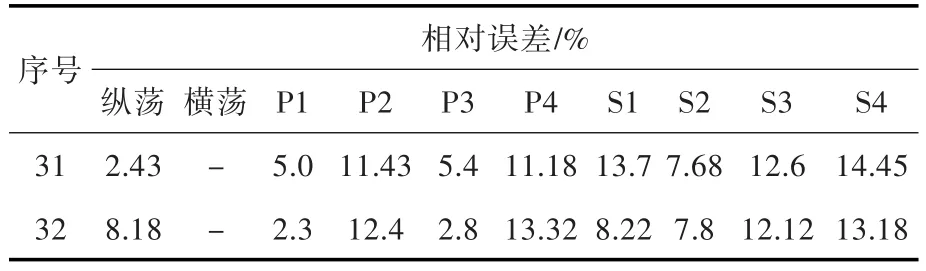
表6 0°浪向下网络的相对误差Table 6 Relative errors of simulation training in 0°wave direction

由测试结果可知，对5个浪向下的时域运动和锚链受力的仿真完全可以满足工程需要，可见依靠BP神经网络的泛化能力代替Moses进行时域计算可行。

根据规范对系泊系统的规定，结合考虑该船在实际作业海域各个浪向的发生概率（表7），采用遗传算法进行了优化设计。以抛锚距离和锚链方位角为设计变量，取浮体纵荡和横荡运动位移最小为优化目标，取上述BP网络得到的仿真训练值并以每根锚链的受力要求作为约束条件。其数学表达如下：

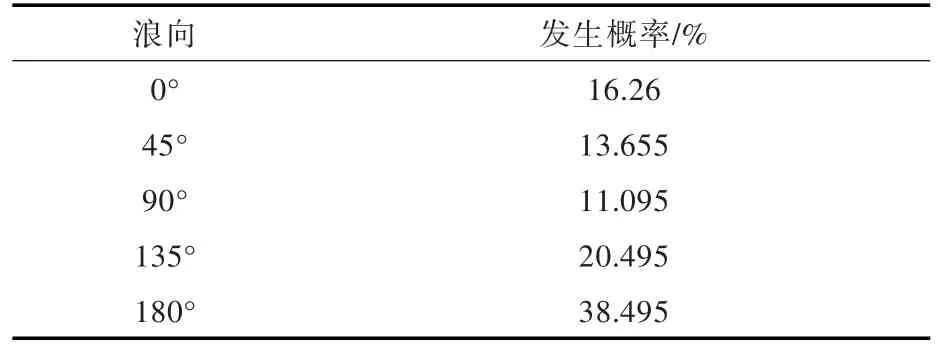
表7 不同浪向的发生概率Table 7 Occurrence probability of different wave directions

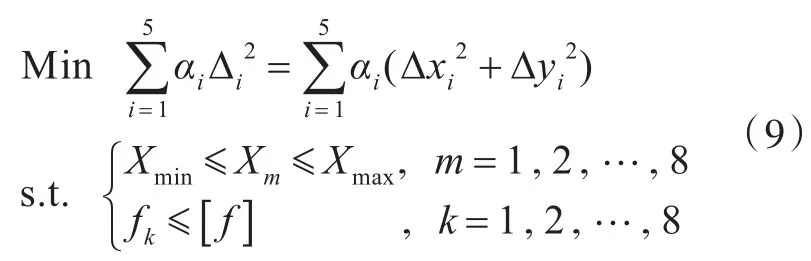
式中：α为浪向发生概率；i为浪向个数，i=5；Δx，Δy分别为纵荡、横荡运动的位移；X为设计变量向量；m为变量个数，m=8；Xmin，Xmax分别为变量边界的下限和上限值，抛锚距离取850～ 2 000 m；fk为每根锚链的受力；[f]为锚链破断力除以安全系数后的值；k为锚链根数，k=8。

运用MATLAB软件的遗传算法工具箱进行计算。因初始种群的随机性，使得每次所得到的最优解均不同，故设定循环计算500次，取其中的最优解，如表8所示。按优化后的方案布置锚链，再次应用Moses软件进行时域计算，并将优化前、后的结果进行对比，如图9所示。

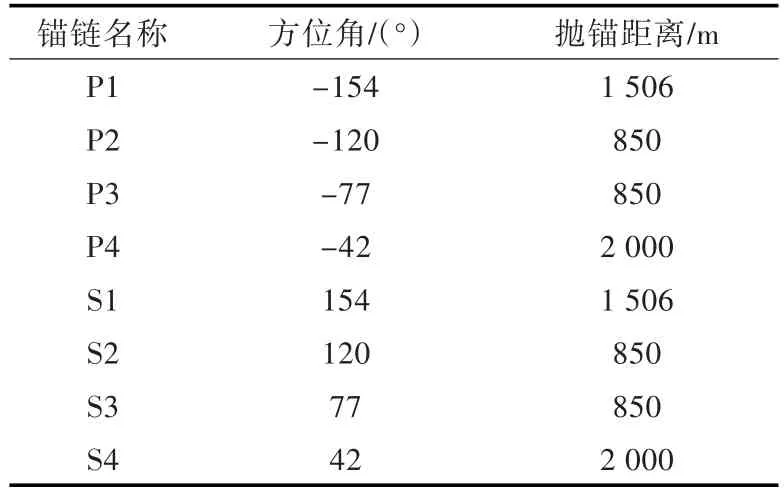
表8 优化后的锚链布置Table 8 Layout of anchor chain after optimization

图9 优化前、后的最大平动位移对比Fig.9 Comparisons of maximum displacement before and after optimization

2.3 小 结

1）由Moses软件计算结果可知，提高锚链的预张力，浮体的纵荡位移会逐渐减小，故可通过增大预张力来改善系泊浮体结构的运动。

2）由BP神经网络对5个浪向下的时域运动和锚链受力的仿真，发现误差均不超过15%，可满足工程需要。因此，用神经网络的泛化能力代替Moses软件的时域计算被认为是可行的。

3）锚链经遗传算法优化布置后，除在0°浪向下结果有所增大外，其余浪向下的平动位移均不同程度地有所减小。其中，90°浪向，也就是横浪下的运动改变最为显著。

4）本文建立的基于BP神经网络和遗传算法的系泊系统优化方法可以为海上浮式结构物的系泊布置提供参考。

3 结 语

本文从工程实际出发，以一艘在南海工作的铺管船为研究对象，考虑环境因素的影响，以锚链的方位角和锚位置作为优化变量，基于BP神经网络和遗传算法对其布置进行了优化设计。在此过程中，还与Moses软件的计算结果进行了对比，发现BP神经网络在满足精度要求的基础上更节省时间，无论是对样本的模拟，还是其优越的预测能力均得到了充分的体现。限于既定的硬件条件以及笔者知识储备的欠缺，本文的结果仍具有一定的局限性，还有待于学者们进行进一步的探讨。

［1］余龙，谭家华.基于准静定方法的多成分锚泊线优化［J］.海洋工程，2005，23（1）：69-73.YU L，TAN J H.Research on optimum multi-component mooring lines based on catenary equation［J］.The Ocean Engineering，2005，23（1）：69-73（in Chinese）.

［2］马小剑，孙昭晨，张志明，等.风流作用下码头系泊船舶缆绳张力及运动量研究［J］.水道港口，2010，31（3）：165-169.MA X J，SUN Z C，ZHANG Z M，et al.A numerical study on mooring line forces and motions of a moored ship under combined action of wind and current［J］.Journal of Waterway and Harbor，2010，31（3）：165-169（in Chinese）.

［3］ALI M T，INOUE Y.On hydrodynamic interaction between two rectangular barges floating side-by-side in regular waves［C］//Proceedings of the International Conference on Mechanical Engineering.Dhaka，Bangladesh：ICME，2005.

［4］严传续，钱宏，项军毅，等.铺管船锚泊定位系统优化设计研究［J］.中国造船，2010，51（1）：84-94.YAN C X，QIAN H，XIANG J Y，et al.Study on design optimization of mooring positioning system for pipelaying vessel［J］.Shipbuilding of China，2010，51（1）：84-94（in Chinese）.

［5］苏晓宇，金鸿章，胡晓东.自动锚泊定位系统的张力混合优化算法［J］.电机与控制学报，2015，19（4）：100-105.SU X Y，JIN H Z，HU X D.Tension hybrid optimization strategy of automatic mooring positioning system［J］.Electric Machines and Control，2015，19（4）：100-105（in Chinese）.

［6］毛建平.基于神经网络的桥梁结构静力有限元模型修正［D］.长春：吉林大学，2011.

［7］朱文龙.基于遗传算法的BP神经网络在多目标优化中的应用研究［D］.哈尔滨：哈尔滨理工大学，2009.

［8］李扬.基于遗传算法的BP神经网络在网络数据抓取中的研究［D］.青岛：中国海洋大学，2010.

［9］许小颖.基于BP神经网络的三体船布局优化研究［D］.天津：天津大学，2013.

［10］张伟.系泊状态下柔性连接多浮体耦合运动研究［D］.天津：天津大学，2008.

［11］吴广怀，沈庆，陈徐均，等.浮体间距对多浮体系统水动力系数的影响［J］.海洋工程，2003，21（4）：29-34.WU G H，SHEN Q，CHEN X J，et al.Influence of the distance between floating bodies on hydrodynamic coefficients of floating multi-body system［J］.The Ocean Engineering，2003，21（4）：29-34（in Chinese）.

［12］WANG J F，LI J D，CAI X G，et al.Hydrodynamic interactions between two bodies in waves in 3D time domain［J］.Journal of Marine Science and Application，2005，4（1）：15-20.

［13］OHKUSU M.On the heaving motion of two circular cylinders on the surface of a fluid［R］.Reports of Research Institute for Applied Mechanics，1969，17（58）：167-185.

Mooring optimization design based on neural network and genetic algorithm

XU Xiaoying1，ZHOU Pan1，WANG Kuan2
1 Department of Mechanical and Electrical Engineering，Wenhua College，Wuhan 430074，China
2 Wuhan Branch of China Classification Society，Wuhan 430074，China

U674.38+1

A

10.3969/j.issn.1673-3185.2017.05.012

2017-01-06< class="emphasis_bold">网络出版时间：

时间：2017-9-26 10:38

文华学院青年基金资助项目（J02e0540211）

许小颖，女，1987年生，硕士，讲师。研究方向：船舶水动力学。E-mail：xuxiaoying52616@163.com

周盼（通信作者），女，1990年生，硕士，助教。研究方向：结构强度分析与设计

http://kns.cnki.net/kcms/detail/42.1755.TJ.20170926.1038.014.html期刊网址：www.ship-research.com

许小颖，周盼，王宽.基于神经网络和遗传算法的系泊优化设计［J］.中国舰船研究，2017，12（5）：97-103.

XU X Y，ZHOU P，WANG K.Mooring optimization design based on neural network and genetic algorithm［J］.Chinese Journal of Ship Research，2017，12（5）：97-103.