教学评价数据的离群点检测算法研究

李 慧，王国强，郭瑞强，高静伟，暴延敏



教学评价数据的离群点检测算法研究

李 慧1,2，王国强1，郭瑞强1,2，高静伟1，暴延敏1,2

(1. 河北师范大学数学与信息科学学院，石家庄 050024； 2. 河北省计算数学与应用重点实验室(河北师范大学)，石家庄 050024)

教学评价是大学教学活动中不可缺少的环节,可能出现故意抬高或压低评分及虚假评分的现象，应该找出这些离群数据并加以清除，以提高学生评教数据的正确性。离群点检测问题是数据挖掘技术的重要研究领域之一，本文实验所用教学评价数据属于分类型数据，目前针对分类型数据的离群点检测算法常用的有基于信息熵的贪婪算法和基于频率的AVF算法。针对贪婪算法时间复杂度较高，AVF算法不够准确的问题，本文提出一种改进的基于频率的离群点检测算法。本文算法首先采用改进的k-modes算法对教学评价数据进行聚类，并提出应用调整的余弦相似度公式作为相似性度量，筛选出远离簇中心的候选离群点，最后通过基于频率的离群点检测算法对候选集进行检测。在真实数据集上的实验表明算法在精确度和效率方面均具有优势。

离群点检测；k-modes聚类；余弦相似度；分类型数据

0 引言

近年来，在教育信息化、远程教育和Web 2.0等应用的带动下,教育数据挖掘（educational data mining，简称 EDM）开始受到越来越多的研究者的关注[1-4]。教育数据挖掘技术综合应用教育学、计算机科学、心理学和统计学等多个学科的理论和技术来解决教育研究与教学实践中的问题，通过分析和挖掘教育相关的数据，EDM技术可以发现和解决教育中的各类问题，如辅助管理人员做出决策、帮助教师改进课程以及提高学生的学习效率等[5]。比如Jingyi Luo，Shaymaa E.Sorour等人利用每节课下课时同学们写下的评论内容，进行学生最终成绩的预测[6]；K. juszczyszyn和A. Prusiewicz Surjeet等人，利用学生选课数据，结合社会网络构造方法，构造学生选课网络，进行学生选课的推荐[7]；Renza Campagni，Donatella Merlini等人利用聚类和序列模式挖掘方法研究由学生自己安排的课程考试顺序对其最终毕业成果之间的影响，以给学生提供更好的学习策略，同时利用挖掘结果给提供更加合理的课程安排[8]。

教学评价是大学教学活动中不可缺少的环节，学生的评教效果依赖于学生对评教的态度和学生对教师的态度，学生评教过程中，如果学生评教态度不认真，或者学生存在偏见必然会扭曲评教结果，因而会出现故意抬高或压低评分及虚假评分的现象，从而出现评教的离群数据，在学生评教过程中，应该找出这些离群数据并加以清除，以提高学生评教数据的正确性。同时由于教学评价数据由学生主观评价得到，所以可以利用教学评价数据进行特殊学生的发现，进一步研究特殊学生的特征与表现，因此，对于教学评价数据的离群点检测方法的研究具有重要意义。

离群点挖掘可揭示稀有事件和现象、发现有趣的模式，有着广阔的应用前景，因此引起广泛关注[9]。离群点检测亦称为离群点挖掘，是数据挖掘的主要任务之一，其目的是消除噪声或发现潜在的、有意义的知识，广泛运用在网络入侵检测、欺诈检测、医疗诊断等领域中[10]。本文研究分类型数据的离群点检测算法及其在大学教学评价中的应用。

针对常用的基于频率的分类型数据离群点检测算法精确度不够高，基于信息熵的贪婪算法时间复杂度高的问题，本文先用基于同现率的改进的K-modes算法对数据进行聚类，去除相似度较高数据，得到候选离群点集合，再通过基于频率的离群点算法对候选离群点集合进行离群点挖掘，从而解决了基于频率算法精确度不够高的问题。经在真实数据集上的实验表明本算法的运行效率与贪婪算法相比较高，并能有效检测出教学评价数据中的离群点数据。

1 相关工作

本文针对教学评价数据进行离群点检测，教学评价共有九项评价指标，每项评价指标有五种评价等级，分别是5优秀、4良好、3中等、2及格和1不及格，属于序数型数据，序数型数据属于分类型数据，本文针对分类型数据的离群点检测算法进行研究。目前，针对分类型的数据，经典的离群点检测算法有基于信息熵的离群点检测算法、基于频率的离群点检测算法。

1.1 基于信息熵的离群点检测算法

He提出了一个基于信息熵的离群点检测算法——贪心算法（Greedy Algorithm）[11]。

信息熵可用于度量数据集的无序和杂乱程度。熵值越大，说明数据集无序和杂乱程度越高；反之，说明数据集越有序和越纯净，无序性越高[12]。这个算法认为，对于数据集D，如果某个对象去掉后，整个数据集的熵值变小，那么这个点就极有可能是离群点。每次找出一个使得熵值变小幅度最大的点，然后从D中去除，再继续查找下一个使得熵值变小幅度最大的点，直到找到需要的n个离群点。基于信息熵的贪心算法，如果要求查找n个离群点，那么就需要扫描整个数据集n+l遍，第一遍统计每个属性值的分布和值域，之后需要查找出n个离群点，因此，需要再扫描n遍，假设用N表示数据集中数据的个数，P表示数据的属性特征的个数，时间复杂度为O（n*N*P）。在需要查找的离群点数目非常大时，贪心算法时间复杂度比较大。

1.2 基于频率的离群点检测算法

Koufakou提出了一个用属性值的频数直接计算离群因子的方法[13]。算法定义每个数据对象的离群因子用AVF（Attribute Value Frequency）表示，计算公式如公式（1）所示，该算法计算数据中每一个数据对象的AVF值，数据对象的AVF值越低，其为离群点的可能性越大。

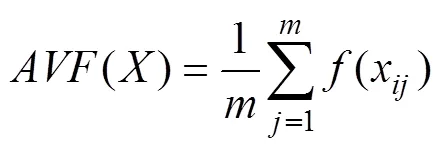
基于频率的离群点检测算法假设所有属性都是相互独立的。对每个属性分别进行计算，并不考虑不同属性相互之间的关系。如果是由几个属性值共同作用的离群点，那么基于频率的离群点检测方法就存在不足，如表1中的示例数据所示。

表1 示例数据

Tab.1 Sample Data

从表1中可以明显看出，第5条记录与其它记录并不相同。但是如果用基于频率的算法检测，得到的结果如表2所示。

表2 频率计算结果

Tab.2 Based on the frequency of the results of the algorithm

表2为根据表1中的数据计算出的频率结果，可以看出第五条记录的频率值要高于另外四个记录的频率值，按照AVF算法的思想，第五条记录无法被检测出来。

2 改进的基于频率的离群点挖掘算法

2.1 算法的基本思路

针对上述基于频率的离群点检测算法的不足，提出一种改进的基于频率的离群点挖掘算法，算法的主要思想是：

第一阶段基于聚类的离群点检测。先用聚类方法对数据进行聚类，去除比较相似的数据。通常含有数据较少的簇被视为离群簇，因此将含有数据较少的类别从类别集合中删去，放入候选离群点集。另外，在基于聚类的离群点检测方法中，可以用对象与它所属类别的簇中心的相似度来度量对象属于簇的程度，计算簇内数据点与所在类别簇中心的相似度，并计算该类别的平均相似度，如果数据点与所在类别簇中心的相似度小于平均相似度，说明该数据点相对来说离群度更高，将这些数据点同样放入候选离群点集中。

第二阶段基于AVF的离群点检测。依据AVF算法对候选离群点集中的数据计算每个数据的AVF值，取最小的n个点放入离群点集中。

2.2 聚类算法的选择

对于分类型数据来说，k-modes算法[14]是常采用的聚类算法。k-modes算法是对k-means算法的扩展。k-modes算法采用相异度来表示k-means算法中的距离，k-modes算法中相异度越小，距离越小。在k-modes聚类算法中，相异度度量方法采用简单的0-1方法，即对象的某一属性与另一对象同一属性值相同，则相异度量值为0。相反，若对象的这一属性与另一对象的同一属性不同，则为1。本文通过聚类实验结果发现这种简单的0、1匹配，用于教学评价数据中并不合理，可能造成聚类结果不正确的问题。

本文聚类实验使用R学院L课程的教学评分数据，实验中把评分数据（5优秀、4良好、3中等、2及格和1不及格）简化为（5,4,3,2,1）。如下面两个表所示，表3为聚类结果中的第一类的九项评分数据，表4为聚类结果的第四类的九项评分的数据。表3第12条数据与类内其他数据差距较大，而与表4的数据更加相似。第一类的聚类中心为（4,4,3,4,4,4,4,3,4），第四类的聚类中心为（3,3,3,3,4,3,3,4,3），按照0–1匹配的相异度度量方法，数据（4,3,1,2,3,2,1,1,2）与第一类聚类中心的相异度为0+1+1+1+1+1+1+1+1=8，与第四类聚类中心的相异度为1+0+1+1+1+1+1+1+1=8，这种相异度度量方式忽略了同一属性下，不同属性值之间的差异，得到了相同的相异度值造成了数据类别分配错误。

除了简单的0、1匹配，Ahmad等人将同一属性下的不同的属性值之间的相异度用它们的共现程度（co-occurence）来反映[15]。

表3 聚类结果第一类

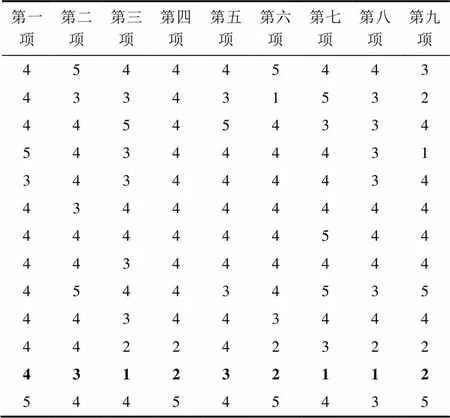
Tab.3 The first kind of clustering results

（2）

表4 聚类结果第四类

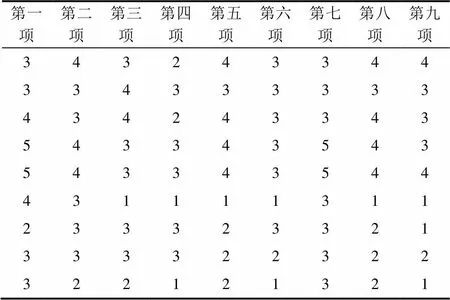
Tab.4 The fourth class clustering results

假设数据集的属性个数为m，对于数据集中任意属性的两个不同取值x和y之间的距离可以表示为：

（4）

改进后的距离度量可以区别同一属性下不同属性的差异，上述碰到的数据类别分配错误问题，根据改进的k-modes算法的相异度计算公式计算得数据（4,3,1,2,3,2,1,1,2）与第一类聚类中心的相异度为5.2203，与第四类聚类中心的相异度为4.8631，根据计算结果数据的类别归为第四类。经观察实验结果发现，改进的k-modes算法用于本文实验数据的整体聚类结果比传统的k-modes算法聚类效果更好，本文采用这种改进的k-modes算法进行聚类，k-modes算法的流程图如图1。

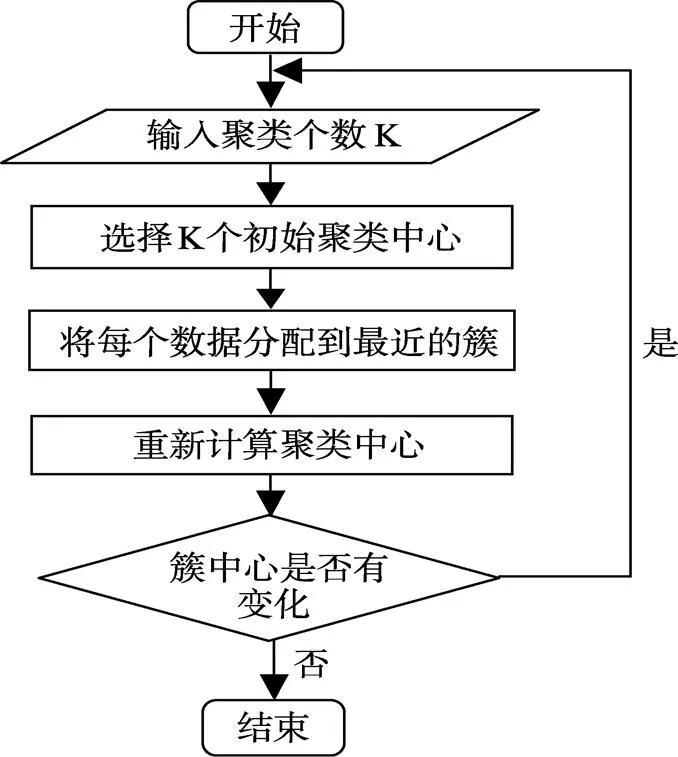
图1 K-modes算法流程图

2.3 调整的余弦相似度度量

余弦相似度是最常见的分类型数据相似度度量方式。余弦相似度（Cosine Similarity）用向量空间中两个向量夹角的余弦值衡量两个个体间差异的大小。公式如下：

余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，余弦值越接近–1，就表明夹角越接近180度，也就是两个向量越不相似。

这种经典的余弦相似度用在学生教学评价数据中存在问题，如X和Y两个学生对教师T的两项评分分别为（1,2）和（4,5），使用余弦相似度得出的结果是0.98，两者极为相似，但从评分上看X和Y对教师T的评价相差很大，需要修正这种不合理性，

调整的余弦相似度，将所有维度上的数值都减去一个均值，比如X和Y的评分均值都是3，那么调整后为（–2,–1）和（1,2），再用余弦相似度计算，得到–0.8，相似度为负值并且差异很大，显然更加符合现实，所以本文在筛选候选离群点时采用调整的余弦相似度作为计算数据与所在类别簇中心之间的相似度的方式。例如表3中的评教数据，簇中心的值为（4,4,3,4,4,4,4,3,4）设簇中心为c，第一行评教数据设为d，那么第一项评教数据与簇中心的调整的余弦相似度计算为：

表3中的各条评价数据与簇中心的调整的余弦相似度如表5。

表5 聚类结果第一类各数据与簇中心的调整的余弦相似度

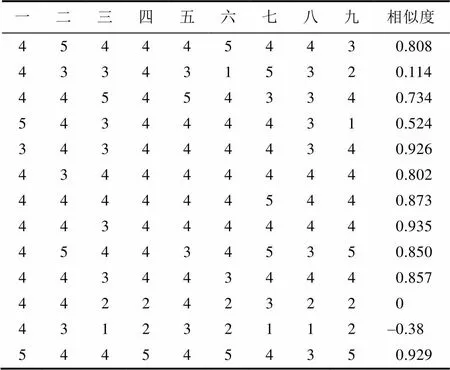
Tab.5 The clustering results of the first kind of various data and the cluster center adjusted cosine similarity

簇中数据与簇中心的平均相似度为0.6135，小于平均相似度的有第2、4、11、12这四条数据，把这四条评教数据放入候选离群点。

2.4 算法的描述

改进的基于频率的离群点检测算法描述如下：

输入：数据集D，聚类个数k，离群点个数n，簇的大小判别阈值t

输出：离群点数据集

1：将数据集D和聚类个数k，作为参数，输入改进的k-modes算法，对数据集D进行聚类。

2：将聚类结果簇中数据个数小于t的放入离群点候选项集，根据公式（5）计算剩余簇中各点到聚类中心的调整的余弦相似度，将余弦相似度小于簇内平均余弦相似度的点放入离群点候选项集。

3：根据公式（1）计算离群点候选项集中每个点的AVF值，先将前n个点按从小到大排序再从第n+1个数据点开始查找，如果与第n个点相比，AVF值更不满足离群点定义，就可以不与其它点进行比较，依次扫描整个数据集。

4：输出n个离群点。

2.5 算法分析

算法共分三个阶段，第一阶段通过改进的k-modes算法进行聚类，第二阶段计算数据与簇中心之间的余弦相似度筛选候选离群点，第三阶段用AVF方法检测离群点。用n表示数据集中数据的个数，m表示数据的属性特征的个数。第一阶段对数据集进行聚类，改进的k-modes算法，时间复杂度为O（n*m*k*t+m2n+m2s3），其中k为聚类个数，t为迭代次数，s为每个属性下相异属性值的数量的平均值。第二阶段的时间复杂度为O（n）。第三阶段的时间复杂度为O（n*m）。因此大致时间复杂度为O（n*m）。基于信息熵的贪婪算法如果需要查找N个离群点，那么就需要扫描整个数据库N+1遍，时间复杂度为O（N*n*m）。在需要查找的离群点数目较大时，贪心算法时间复杂度比较大。

3 实验与分析

3.1 数据预处理

本研究所用的数据存储在Oracle数据库中，所用的数据涉及的表有学生信息表、学生选课表、学生评教评分表、课程信息表、教学任务表、教师信息表。这些表中的数据独立存在，我们需要将数据整理成数据挖掘工作需要的形式，对数据进行预处理。数据预处理工作的主要任务是对数据进行数据清洗、集成、变换和规范化，将数据整理成需要的格式。首先在数据库中创建汇总表视图，先对学生信息表进行清洗，删掉没有按时报到的学生数据，然后联合查询这六张表，得到包含学年、学期、学院、班级、选课课号、学号、课程代码、课程性质、课程归属、学分、教师工号、评教号、评分、评价等级等字段的学生评教综合信息表。

表6 原始数据形式

Tab.6 Raw data form

对数据进行转化，将数据转化为挖掘实验所需的评分数据矩阵的形式，如表7所示，每一行数据包含一个学生对教师T的9项评分，经过预处理之后的数据更加规整，方便之后的数据挖掘工作。

3.2 实验结果及对比

为验证算法的有效性与效率，将通过实验来比较本文所提出的算法、与贪婪算法和基于频率的离群点检测算法各自的性能。实验的硬件环境是 CPU1.7GHz，主存4GB，软件环境为 Matlab 2014、Sublime Text 3、Echarts3。实验所用的数据集是H高校的大学教学评价数据，由于原始数据集非常庞大，仅从经过预处理后的评分矩阵数据集里筛选出R学院C班程序设计的评分矩阵作为实验数据。C班共50名学生，教学评价共有九项评价指标，每项评价指标有五种评价等级，分别是5优秀、4良好、3中等、2及格和1不及格，实验中将评分等级数据简化为5、4、3、2、1。数据形式如表7所示。下面从准确性和效率两个方面，分析算法的性能。

（1）算法的准确性

利用Echarts3.0插件对检测结果进行平行坐标可视化进而验证算法的准确性，利用贪婪算法进行离群点检测结果如图2，利用AVF算法进行离群点检测结果如图3，本文提出的算法的检测结果如图4。图中的11个平行坐标轴，分别代表学生的ID号、九项评价指标和数据的检测结果，图中的细实线代表非离群数据，菱形线、粗实线和虚线三条线分别代表检测到的三个离群点。

图2中菱形线为离群点1，粗实线为离群点2，虚线为离群点3。从图中可以看出，三条离群数据线明显偏离正常数据，贪婪算法检测结果比较理想。

图3中菱形线为离群点1，粗实线为离群点2，虚线为离群点3。从图中可以看出离群点1的数据与正常数据无明显的偏差，不应判断为离群数据，AVF算法的检测结果不准确。

图4中菱形线为离群点1，粗实线为离群点2，虚线为离群点3。从图中可以看出三条离群数据线明显偏离正常数据，所以本文提出算法可以有效的检测出离群点，且与AVF算法相比本文所提出的算法的检测结果更加准确，与贪婪算法的检测结果相同。

表7 实验所需数据矩阵形式

Tab.7 Experimental data required for the matrix form

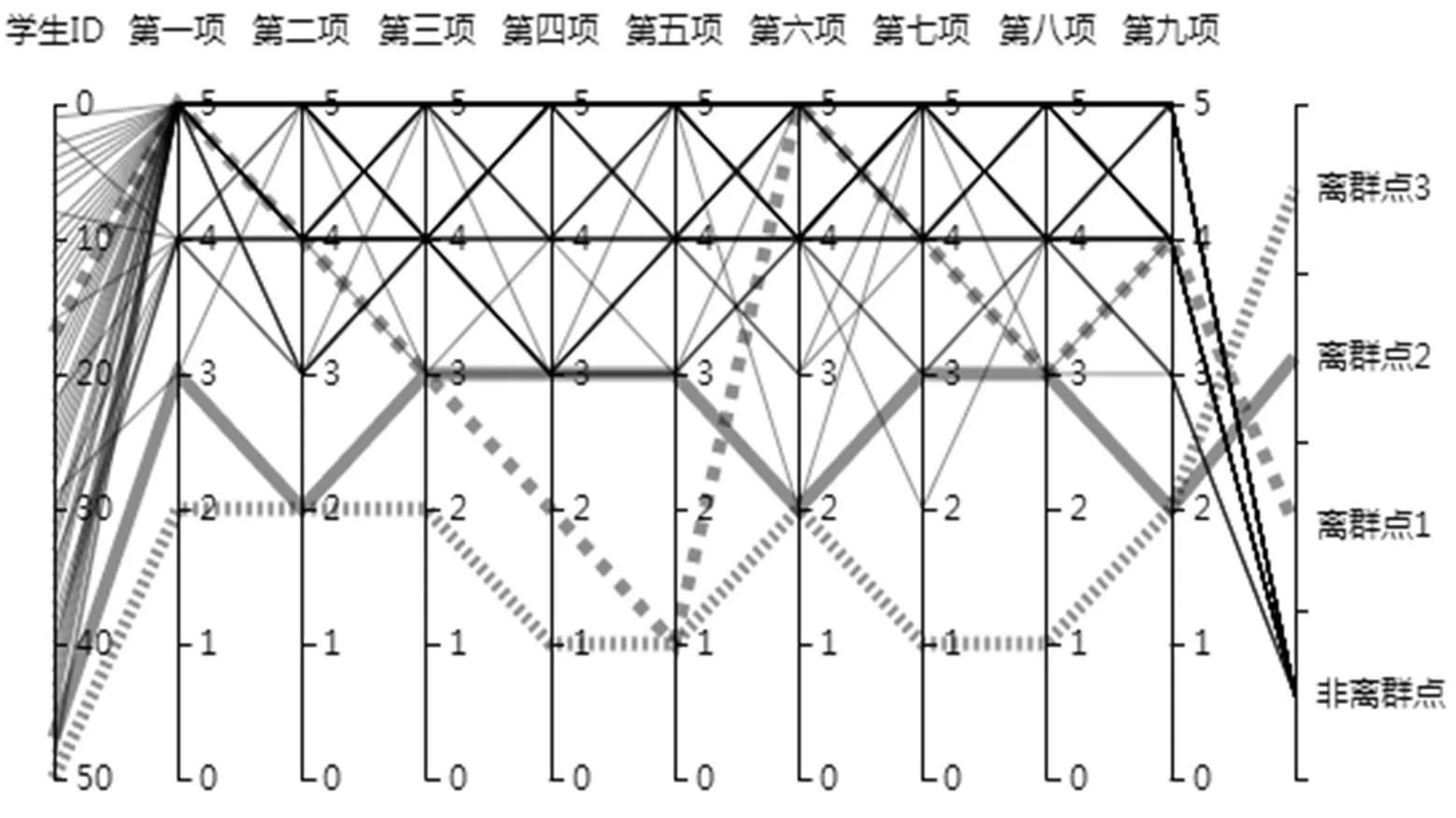
图2 贪婪算法的离群点检测结果

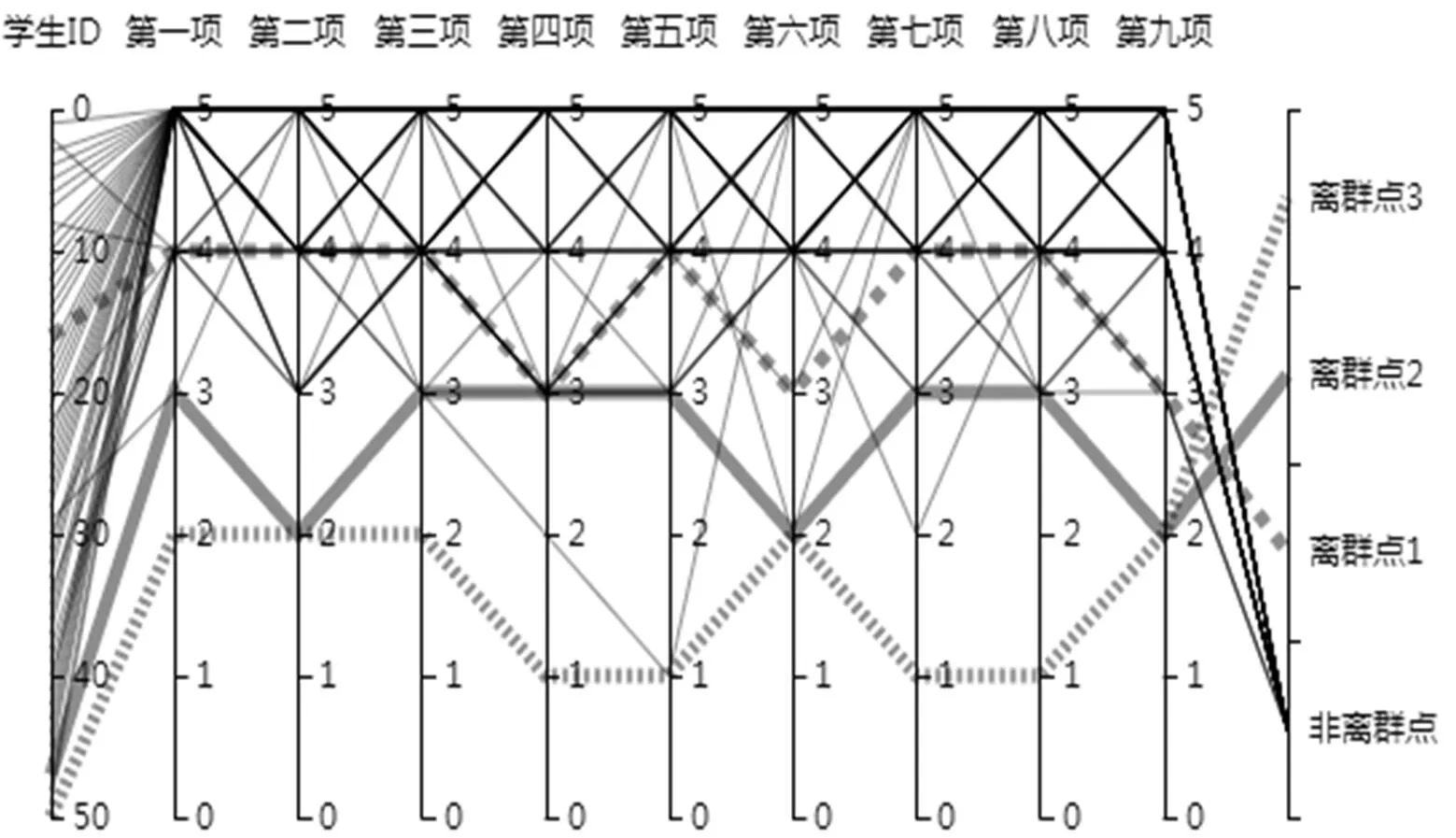
图3 AVF算法离群点检测结果的可视化

图4 本文的离群点检测算法检测结果的可视化

（2）算法的效率

三种算法的运行时间对比如下：

从图5中可以看出，三个算法中，执行时间最短的是AVF算法，贪心算法的执行时间最长，本文提出的算法的执行时间在和贪心算法之间。主要是因为本文提出的算法经过了聚类算法，导致执行时间高于AVF算法。因此，我们可以看出本算法仍是一种比较高效的算法。

图5 三个算法的运行时间对比图

4 结束语

本文算法先采用改进的k-modes算法对教学评价数据进行聚类，再根据簇内数据与簇中心之间的调整的余弦相似度的值筛选出候选离群数据集，最后通过基于频率的离群点检测算法对候选离群项集进行离群点的检测，进而得到最后的离群点，既改善了基于频率的离群点检测算法精度不够高的问题，又利用了基于频率的离群点检测算法的高效率的优点，与基于信息熵的贪婪算法相比效率较高。算法可以有效的检测出教学评价数据中的离群点，由于教学评价中的离群点检测方法的研究还比较少，在下一步的工作中，笔者打算将本文提出的算法应用与R学院的所有教学评价数据中，探索教学评价数据中的全局离群点，情景离群点和集体离群点的情况，并结合其它数据对离群点进行解释，以给学校的教学工作提供意见。

[1] Anjewierden A, Kolloffel B, Hulshof C.Towards educati-onal data mining: Using data mining methods for automat-ed chat analysis to understand and support inquiry learning processes. In: Proc. Of the Int’l Workshop on Applying Data Mining in e-Learning (ADML 2007), 2007.

[2] 黎未然. 数据挖掘技术在数字化校园建设中的应用[J]. 软件, 2012, 33(10): 61-63.

[3] 栾红波, 文福安. 数据挖掘在大学英语成绩预测中的应用研究[J]. 软件, 2016, 37(3): 67-69.

[4] 胡健, 王理江. 数据挖掘在选课推荐中的研究[J]. 软件, 2016, 37(4): 119-121.

[5] 周庆, 牟超, 杨丹. 教育数据挖掘研究进展综述[J]. 软件学报, 2015, 26(11): 3026-3042.

[6] Jingyi Luo, Shaymaa E.Sorour, Kazumasa Goda, Tsunen-ori Mine. Predicting Student Grade based on Free-style Comments using Word2Vec and ANN by Considering Prediction Results Obtained in Consecutive Lessons. EDM 8th, Jun 26-29, 2015.

[7] Agnieszka Prusiewicz. Educational Services Recommen- dation Using Social Network Approach. Intelligent Infor- mation and Database Systems, 2011, 6591: 327-336

[8] Renza Campagni, Donatella Merlinii. Data mining models for student careers[J]. Expert Systems with Applications, 2015(13): 5508-5521.

[9] 薛安荣, 姚林. 离群点挖掘方法综述[J]. 计算机科学, 2008, 35(11): 13-18.

[10] CASSISI C, FERRO A, ROSALBA G. Enhancing density-based clustering: parameter reduction and outlier detection[J]. Information Systems, 2013, 38(3): 317-330.

[11] He Z, Deng S, Xu X. A fast greedy algorithm for outlier mining[C]. Proceedings of Pacific-Asia Conference on Knowledge Discovery and Data Ming, pages 567-576, Seoul-Korea, 2006.

[12] COVER T M, THOMAS J A. Elements of information theory[M]. 2nd ed. New Jersey: Wiley & Sons, 2006.

[13] Koufakou A, Ortiz E G, el al. A Scalable and Efficient Outlier Detection Strategy for Categorical Data[C]. Proc. Of the 19th IEEE International Conference on Tools with Artificial Intelligence, Washington DC, 2007, 210-217.

[14] Z. Huang. Extensions to the K-Modes algorithm for clustering large data sets with categorical values[J]. Data Min. Knowl. Disc. 2(3), 1998: 283-304.

[15] Amir Ahmad, Lipika Dey. A k-mean clustering algorithm for mixed numeric and categorical data[J]. Data & Knowledge Engineering, 2007, 503-527.

Research on Outlier Detection Algorithm Based on Teaching Evaluation Data

LI Hui1,2, WANG Guo-qiang1, GUO Rui-qiang1,2, GAO Jing-wei1, BAO Yan-min1,2

(1. College of Mathematics and Information Science, Hebei Normal University, Shijiazhuang 050024; 2. Key Laboratory of Computational Mathematics and application Hebei Normal University, Hebei Province, Shijiazhuang 050024)

Teaching evaluation is an indispensable link in university teaching activities. In the process of teaching evaluation, some students may raise or reduce scores on purpose or do not take the evaluation seriously, in order to improve the correctness of the evaluation, we should detect and clear the outlier data. Outliers detection problem is one of the important research field of data mining technology. The experimental data of this paper is categorical data,currently outlier detection algorithm for categorical data commonly use greedy algorithm based on information entropy, and AVF algorithm based on frequency. In view of the greedy algorithm time complexity is high, and the AVF algorithm is not accurate enough, this paper proposes an improved outlier detection algorithm based on the frequency. The proposed algorithm first using the improved k-modes algorithm to cluster the teaching evaluation data, and put forward using the Adjusted cosine similarity formula as the similarity metric to screen out candidate outliers far from cluster center, finally detect the outlier from candidate selection by AVF algorithm. Experiments on real data sets show that the algorithm has advantages in terms of accuracy and efficiency.

Outlier detection; K-modes clustering; Cosine similarity;Categorical data

TP391

A

10.3969/j.issn.1003-6970.2017.04.004

河北师范大学教改课题资助(2015XJJG023)。

李慧(1993-)，女，研究生，主要研究方向为数据挖掘；郭瑞强(1974-)，男，教授，主要研究方向为数据库，数据仓库，数据挖掘；高静伟(1972-)，男，副教授，主要研究方向为计算机应用；暴延敏(1992-)，女，研究生，主要研究方向为数据挖掘。

王国强，男，实验师，主要研究方向为计算机应用。

本文著录格式：李慧，王国强，郭瑞强，等. 教学评价数据的离群点检测算法研究[J]. 软件，2017，38（4）：18-25