基于复杂网络异质性的节点重要性评估方法

黄加增



基于复杂网络异质性的节点重要性评估方法

黄加增

（福建农林大学东方学院，福建福州 350017）

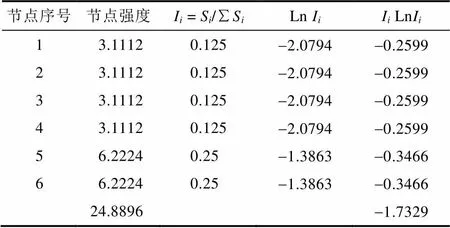
对于复杂网络的结构特殊性，用加权拓扑熵为理论基础，提出了基于复杂网络结构异质性变化率的节点重要程度评估方法。首先，本文给出了复杂网络加权拓扑熵的概念，阐述了基于BBV网络的反向演化原理，其次，在反向演化原理的基础上提出了节点重要程度取决于网络结构异质性变化率的观点，并提出了网络割点的异质性变化率的计算方法；最后，以一个例子来说明节点重要程度的评估过程，并对特殊节点进行了处理分析。

复杂网络，加权网络，加权拓扑熵，异质性变化率，节点重要程度评估

0 引言

研究复杂网络节点重要性方法主要有两种：社会网络分析方法和系统科学方法。其中，社会网络分析方法的主要思想是“假设显著性等价于重要性”，其强调的是节点在网络中发挥的作用和功能，即通过度量某个节点与网络中其他节点的连接数量来衡量这个节点在网络中的重要程度[1-3]，一般地是以节点度（Degree）、介数（Betweenness）、接近度（Closeness）等各种不同的指标加以衡量；系统科学方法的主要思想是“假设破坏性等价于重要性”，其原理是以计算某个节点失效后会给网络带来的破坏程度衡量其重要性[4-11]，如PageRank、HITS、SALSA、PopRank、ObjectRank和RealWalk等较为经典的算法。

我国研究学者在节点重要性评估方面也做了许多的工作，特别是在第二种研究方法方面有许多较为突出的贡献，如席酉民和唐方成等提出的“核与核度理论”[12,13]，李振华和陈贵海等提出的“分点”概念[14]等。

目前大部分的网络都是加权网络（Weighted Network），网络中的每条边用来说明连接两个节点之间是否存在，而且还显示了这种连接的某种特性（如流量的大小）；当然，每个节点在网络中也扮演着不同角色，具有不完全相同的属性和能力。无论是技术网络方面的公共交通道路网络、Internet网络，还是科学家合作网络、引文网络等社会网络，都在不同的侧面显示出其加权网络的特性[15-17]。

对于上述两种研究方法，针对加权网络，通过引入能够表征全局状态的熵及其熵变理论，提出了以网络加权拓扑熵的变化量作为节点重要程度的观点。一方面，以加权网络中的边权和节点强度等属性不仅可以表明节点在网络中的不同位置和连接特性，而且还可以充分体现某些处于网络边缘的关键节点（如计算机网络中的网关、服务器等节点）的重要性；另一方面，通过能体现网络整体状态的熵的变迁衡量不同节点被删除后对网络所产生的破坏程度。

1 网络加权拓扑熵

在信息论中，申农（Claude E. Shannon）将信息熵定义为离散随机事件的出现概率，或者说是信息熵是消除不确定性的一种度量。仿照信息熵的定义，谭跃进等人提出了网络结构熵的概念，并将其引入到网络异质性的研究中。在文献[18]中，谭跃进将无标度网络的网络结构熵定义为，其中：，为节点的度。这个定义的基本假设是：网络节点的重要程度完全由这个节点的度所决定。

由于上述假设的缺陷，以及上述定义无法描述加权复杂网络的拓扑状况，本文提出了能够描述加权复杂网络异质性的定义：

和一般意义上的熵一样，网络加权拓扑熵也具有极值，即当网络结构完全均匀时，网络加权拓扑熵达到其极值。可以很方便地证明这个极值的存在：

首先，当网络完全均匀时，所有的边权都会取同样的权、所有的节点都具有相同的节点强度。事实上，这时的网络加权拓扑熵已经和谭跃进教授的网络结构熵没有任何区别。

因此，在网络完全均匀时网络加权拓扑熵取的极值为：

2 加权网络的演化

2.1 节点加入网络时的演化

以BBV加权网络为例，当某个节点加入网络并与若干个节点相连时，相关边权和节点强度按照下列方式进行演化：

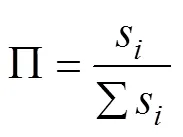
即节点强度越大被选中的可能性也越大。

（3）

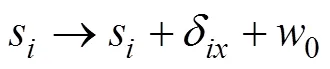
（5）

2.2 节点退出网络时的演化

在BBV加权网络中，当某个节点退出网络时，网络中边的权重和节点的强度都会发生演化，也就是说这种演化同样会发生在有节点退出的相关局域网络中。

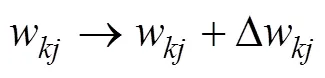
（7）

（8）

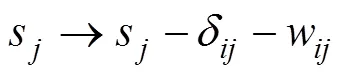
（10）

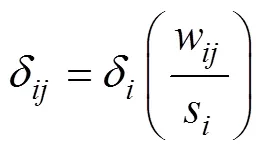
简单证明如下：

3 网络异质性变化率与节点重要性评估

网络加权拓扑熵表征了加权网络拓扑结构的异质性，是一种能够描述加权网络整体状态的指标。只要网络结构发生改变，网络加权拓扑熵也会随之发生改变。

对于加权网络而言，当某个节点退出网络后，网络中相关的边权和节点强度都会发生变化，从而导致网络异质度也随之发生变化。因此，我们可以通过网络异质度的变化率来判断不同节点在网络中的重要性。

在网络中，可能会存在一些称为“割点”（cut vertex）的特殊节点，一旦这种节点退出网络后，则网络会被分割成若干个独立的连通子网。

根据反向演化原理，具有较大强度的节点退出网络时，不仅仅是网络节点的减少，而且也导致原来由退出节点所承担的负荷被分配到其它节点上，从而使得网络的异质性发生改变。

根据加权拓扑熵的变化，当某节点退出网络时，网络异质性有以下演化特性：

（1）节点的度越大，该节点的退出对网络的异质性影响就越大；

（2）与节点直接相连边的权越大，该节点的退出对网络的异质性影响就越大；

（3）分摊了来自于别的节点的负荷越大，该节点的退出对网络的异质性影响就越大。

因此，可以将不同节点退出前后的网络异质性变化率作为评估这些节点在网络中的重要程度的依据。

4 举例与分析

下面以一个示例对本文提出的节点重要程度评估方法加以说明：

图1是一个加权网络的拓扑图，分别用基于异质度的变化率和基于节点度的方法进行节点重要性的评估。

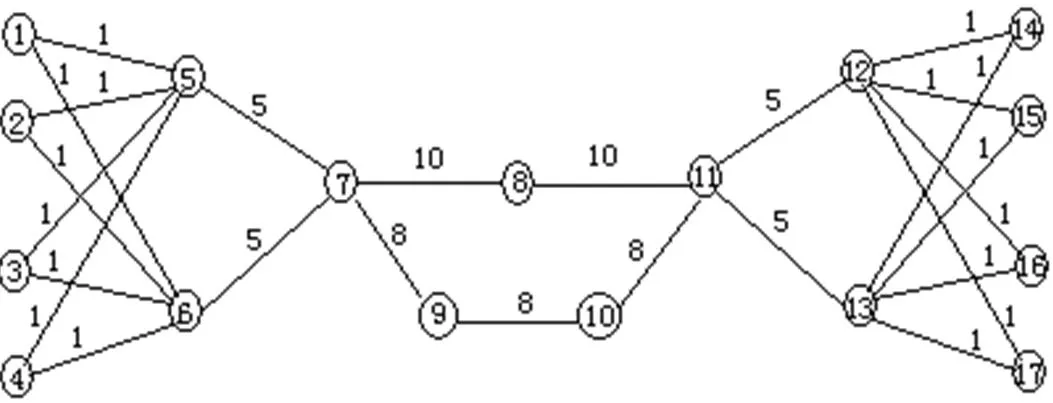
图1 一个加权网络的拓扑图

假设该网络共有17个节点，各边的权值分别如图所示。表1是根据该网络的结构和边权所计算的结果：

表1 初始计算结果

Tab.1 Initial results

下面分别计算不同节点退出网络后，加权熵及其相关参数的变化情况。尽管任何一个节点退出后，对于连通网络内的各个节点的强度和边权都会产生影响，在这里仅考虑与退出节点有直接连接的节点及其相关边所发生的变化。

4.1 节点1退出网络时

表2 节点1退出网络后的各参数变化

Tab.2 Parameter changes of node 1 after exiting the network

根据表2，节点1退出网络后，网络拓扑经过演化，其加权拓扑熵为：。

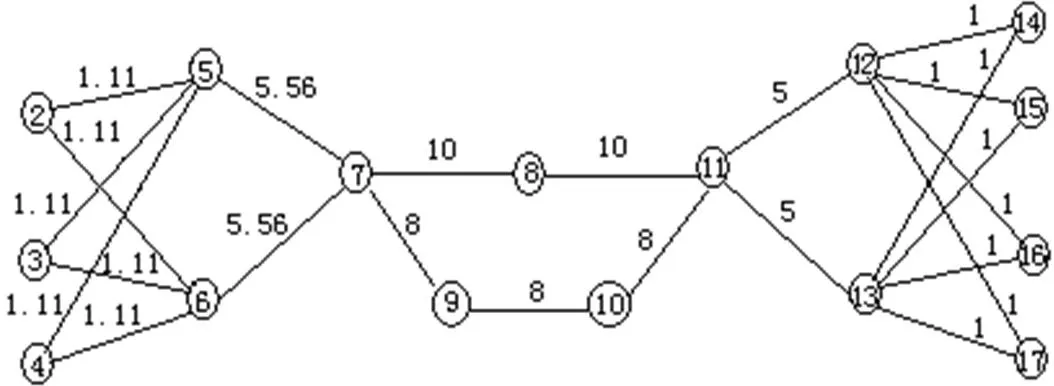
图2 节点1退出后网络的加权拓扑结构

同理，节点2、节点3、节点4、节点14、节点15、节点16和节点17等分别退出网络后，网络加权拓扑熵也同为2.381。

4.2 节点5退出网络时

与节点5有直接连边的节点分别为节点1、节点2、节点3、节点4和节点7。其中前4个节点除了与节点5有连接外，还与节点6有连接；而节点7则还与节点6、节点8和节点9有连接。节点5的退出，使得原来由节点5承担的负荷都要被转嫁到节点6上。

表3 节点5退出网络后的各参数变化

根据表3，节点5退出网络后，网络拓扑经过演化，其加权拓扑熵为：。

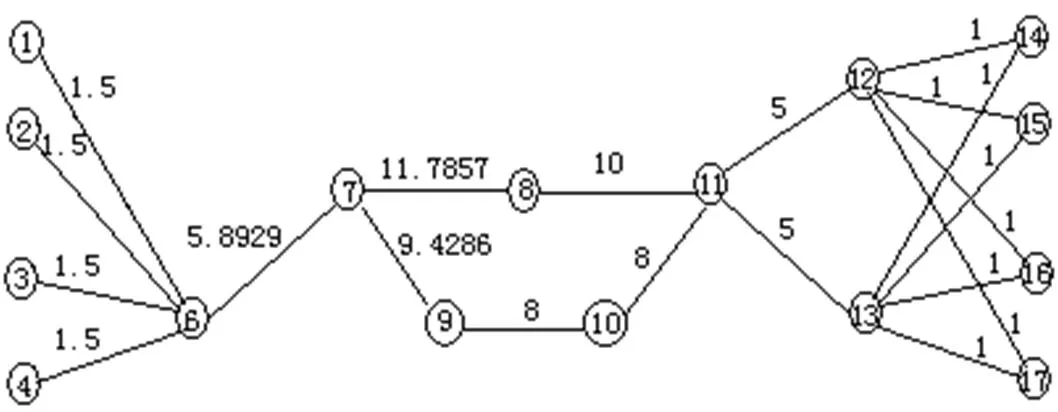
图3 节点5退出后网络的加权拓扑结构

同理，节点6、节点12和节点13等分别退出网络后，网络加权拓扑熵也同为2.3082。

4.3 节点7退出网络时

与节点7有直接连边的节点分别为节点5、节点6、节点8和节点9。节点7的退出，导致网络分为两个连通分支，网络结构发生重大变化。其中，第一个连通分支由节点1~节点6组成，共有6个节点；第二个连通分支由节点8~节点17组成，共有10个节点。

表4 节点7退出第一个连通分支的各参数变化

Tab.4 The parameters of node 7 exiting the first connected branch

表5 节点7退出第二个连通分支的各参数变化

Tab.5 Node 7 exits the parameters of the second connected branches

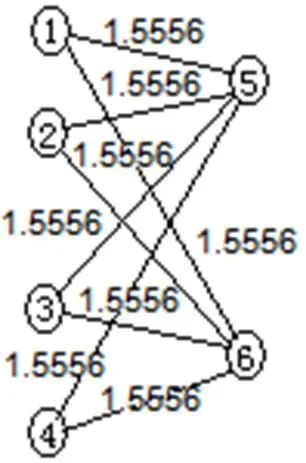
图4 节点7退出后网络的加权拓扑结构

同理，节点11退出网络后，网络加权拓扑熵也为1.8496。

4.4 节点8退出网络时

与节点8有直接连边的节点分别为节点7和节点11。其中，节点7除了与节点8有连接外，还与节点5、节点6和节点9有连接；而节点11则还与节点10、节点12和节点13有连接。节点8的退出，使得原来由节点8承担的负荷都要被转嫁到节点7和节点11上。

表6 节点8退出网络后的各参数变化

Tab.6 Parameter changes of node 8 after exiting the network

根据表6，节点8退出网络后，网络拓扑经过演化，其加权拓扑熵为：。

图5 节点8退出后网络的加权拓扑结构

4.5 节点9退出网络时

与节点9有直接连边的节点分别为节点7和节点10。其中，节点7除了与节点9有连接外，还与节点5、节点6和节点8有连接；而节点10则还与节点11有连接。节点8的退出，使得原来由节点9承担的负荷都要被转嫁到节点7和节点10上。

表7 节点9退出网络后的各参数变化

Tab.7 Parameter changes of node 9 after exiting the network

根据表7，节点9退出网络后，网络拓扑经过演化，其加权拓扑熵为：。

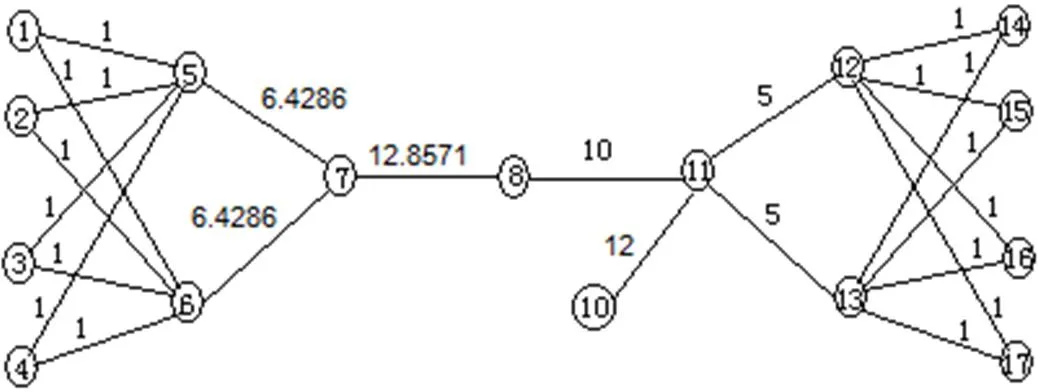
图6 节点9退出后网络的加权拓扑结构

同理，节点10退出网络后，网络加权拓扑熵也为2.3121。

4.6 对比与分析

通过对加权拓扑熵的计算，可以看到：不同节点的退出对网络的异质性所带来的影响各不相同，特别是割点的退出对网络的异质性影响尤为重大。表8描述了网络异质性变化率与节点度两种不同的节点重要程度评估方法的对比。

表8 异质性变化率与节点度对比表

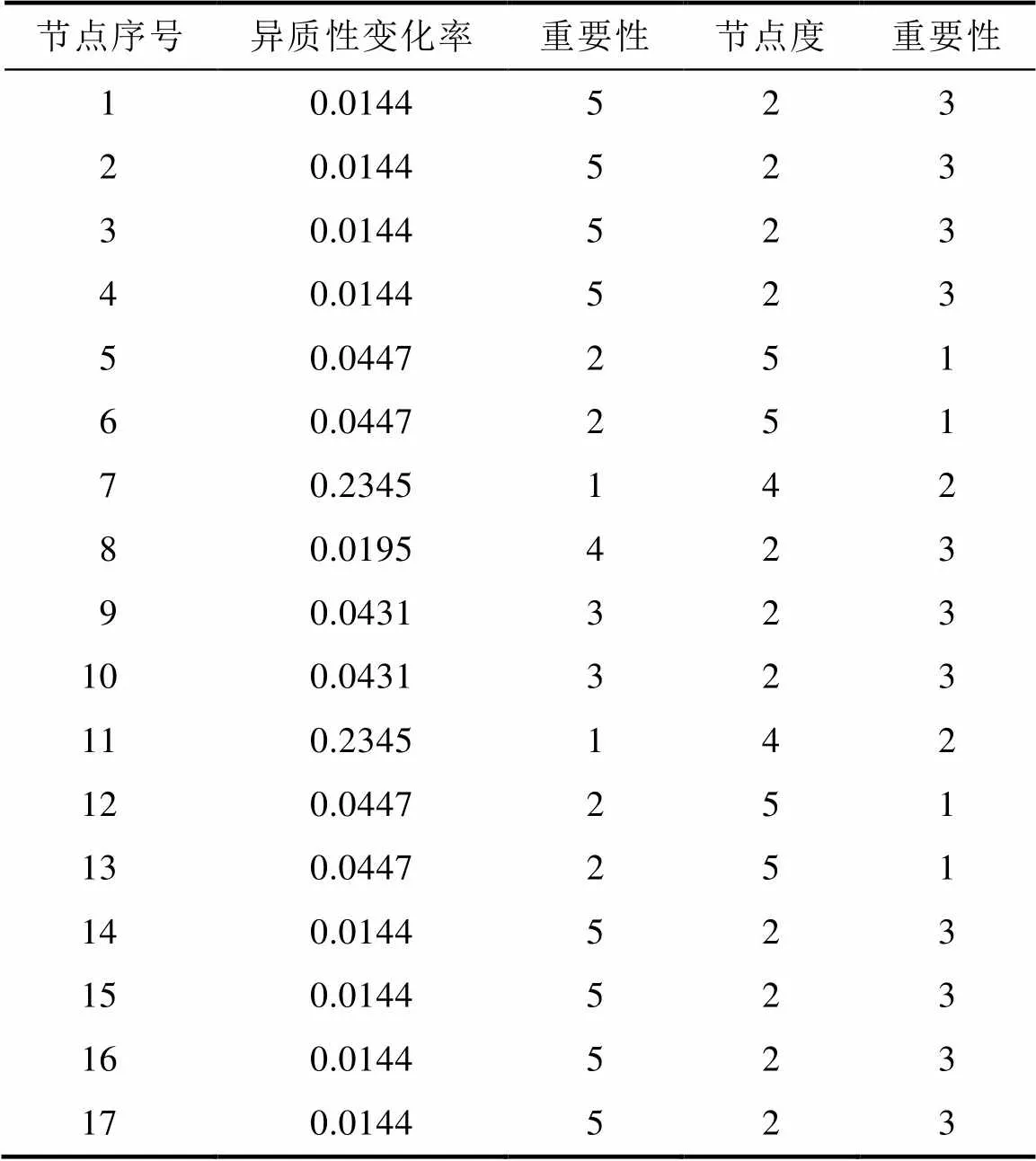
Tab.8 Comparison table of heterogeneity change rate and node degree

从表中可以看到：

根据节点度方法的重要程度评估中，节点5、节点6、节点12和节点13为最重要的节点，因为这几个节点的度最大；而根据异质性变化率进行的评估则认为节点7和节点11的重要程度最高，因为这两个节点所到导致的异质性变化率最高。从实际来看，这样的结论也是合理的，因为节点7和节点11都是网络的割点，不论是节点7还是节点11，只要退出网络，则都会导致网络连通性的破坏，而且所形成的两个连通分支都具有较大的规模。

比较有意思的是节点8、节点9和节点10之间的重要程度排序。由于节点9和节点10是对称关系，所以这里只讨论节点8与节点9的重要程度排序：

● 当节点8的节点强度小于节点9时，节点9的重要程度就大于节点8；

● 当节点8的节点强度大于节点9的节点强度，但不超过2倍时，节点9的重要程度就大于节点8；

● 当节点8的节点强度达到节点9的节点强度2倍时，节点8的重要程度就大于节点9。

除此而外，基于网络异质性变化率的节点重要程度评估方法还具有划分层次更加丰富的特性。如上述例子中，根据节点度的方法只划分了3个层次的重要程度，而根据异质性变化率的方法则划分出了5个不同的层次。丰富的层次可以为网络的管理和维护提供更加可信的依据。

5 总结

熵是一个能够反映系统整体状态及其演化的指标。本文从整体观点进行网络节点重要程度评估方法的研究，并在BBV网络的基础上，提出了基于网络异质性变化率的评估方法。该方法具有以下一些特点：

（1）以网络拓扑结构的演化研究各节点在网络中所发挥的作用，具有整体的视点，克服了诸如节点度方法等的局部观点所固有的缺陷。

（2）通过边权和节点强度计算，可以实时的反应节点重要程度的动态变化。

（3）采用影响因子的方式解决了多个连通分支时的异质性变化率的计算问题。

（4）以异质性变化率作为衡量的指标，从而丰富了重要程度的层次。

总之，异质性变化率的评估方法为网络脆弱性的研究，并且能够为日常的网络管理、维护和安全防范等都提供重要的依据。

[1] Albert R, Jeong H, Barabási A L. Error and attack tolerance of complex networks[J]. Nature. 2000, 406: 378-382.

[2] Reuters. Scientists spot Achilles heel of the Internet . United States: CNN, 2000 [2005207215]. http://archives.cnn.com/ 2000/TECH/computing/07/26/science. internet. reut/

[3] [3] Poulin R , Boily M C , Masse B R. Dynamical Systems to Define Cent rality in Social Networks[J]. Social Networks, 2000, 22: 187-220

[4] Lempel R, Moran S. The stochastic approach for link- structure analysis (SALSA) and the TKC effect. Computer Networks, 2000, 33(126): 387-401

[5] Nie Z, Zhang Y, Wen J-R, Ma W-Y. Object-level ranking: Bringing order to Web objects//Proceedings of the www. Chiba, Japan, 2005: 567-574

[6] Balmin A, Hristidis V, Papakonstantinou Y. Object rank : Authority-based keyword search in databases//Proceedings of the VLDB. Toronto, Canada , 2004: 564-575

[7] Geerts F, Mannila H, Terzi E. Relational link-based ranking// Proceedings of t he VLDB. Toronto, Canada, 2004: 552-563.

[8] Ding L, Pan R, Finin T, Joshi A, Peng Y, Kolari P. Finding and ranking knowledge on t he semantic Web//Proceedings of t he ISWC. Galway, Ireland, 2005: 156-170

[9] Guimera R. Classes of Complex Networks Definedby Role- to-role Connectivity Profiles[J]. Nature Physics, 2007 (3): 63-69

[10] 于会, 刘尊, 李勇军. 基于多属性决策的复杂网络节点重要性综合评价方法[J]. 物理学报, 2013, 62(2), 1-9 YU H, LIU Z, LI Y J. Key nodes in complex networks identified by multi-attribute decision-making method[J]. Acta Physica Sinica, 2013, 62(2), 1-9. (in Chinese)

[11] 胡平, 王文, 刘志华. 综合节点异质性、删除及DPA的网络演化模型[J]. 管理科学学报, 2011(8), 1-7, 16 HU P, WANG W, LIU Z H. Evolving network model of integrating three mechanisms: Node otherness, uniform node deletion and double preferential attachment[J]. Journal of management sciences in China, 2011(8), 1-7, 16. (in Chinese)

[12] Lusseau D , Newman M E J . Identifying the Role that Animals Play in Their Social Networks[C] Proceedings of the Royal Society of London Series B-biological Sciences , 2004 , 271(10): 477-481

[13] 席酉民, 唐方成. 组织的立体多核网络模型研究[J]. 西安交通大学学报, 2002, 36 (4) : 430-435. XI Y M, TANG F C. Research of organizational multiplex multi-kernel network model[J]. Journal of xi’an jiaotong university, 2002, 36 (4): 430-435. (in Chinese)

[14] 李振华, 陈贵海, 邱彤庆. 分点: 无结构对等网络的拓扑关键点[J]. 软件学报, 2008, 19(9): 2376-2388. LI Z H, CHEN G H, QIU T Q. Partition node: topolog­ically-critical nodes of unstructured peer-to-peer networks[J]. Journal of software, 2008, 19(9): 2376-2388. (in Chinese)

[15] 郝彬彬, 井元伟, 张嗣瀛. 复杂网络度分布的异质性对其同步能力的影响[J]. 东北大学学报: 自然科学版, 2008(11), 1521-1524 HAO B B, JING Y W, ZHANG S Y. Effect of heterogeneous distribution of degree on synchronization in complex networks[J ]. Journal of Northeastern University(Natural Science). 2008, (11), 1521-1524. (in Chinese)

[16] 王班, 马润年, 王刚, 陈波. 改进的加权网络节点重要性评估的互信息方法[J]. 计算机应用, 2015, 35(7), 1820-1823, 1828. WANG B, MA R N, WANG G, CHEN B. Improved evaluation method for node importance based on mutual information in weighted networks[J]. Journal of Computer Appli­cations, 2015, 35(7), 1820-1823, 1828. (in Chinese)

[17] 朱鹏鹏, 董建民, 李慧嘉. 节点重要性指标在加权网络中的应用[J]. 计算机安全, 2013(4), 47-49 ZHU P P, DONG J M, LI H J. Application of vertex centrality indices to weighted networks[J]. Netword and computer security, 2013(4), 47-49. (in Chinese)

[18] 谭跃进, 吴俊. 网络结构熵及其在非标度网络中的应用[J]. 系统工程理论与实践, 2004, 24(6): 1-3. TAN Y J, WU J. Network structure entropy and its application to scale-free networks[J]. Systems engineering- theory and practice, 2004, 24(6): 1-3. (in Chinese)

Node Importance Evaluation Method Based on the Heterogeneity of Complex Networks

HUANG Jia-zeng

(Dongfang College, Fujian Agriculture and Forestry University, Fujian, Fuzhou 350017)

For the special structure of complex networks, weighted topological entropy theory, evaluation method of node important degree of heterogeneity of complex network structure based on the rate of change is proposed. Firstly, this paper gives the concept of weighted complex network topological entropy, elaborated the BBV network based on evolution principle, secondly, based on the principle of reverse evolution the proposed node important degree depends on the heterogeneity of network structure change rate of view, and puts forward the calculating method of heterogeneous change network cut point rate; finally, with an example to illustrate the evaluation process of node important degree, and the special nodes were analyzed.

Complex network; Weighted network; Weighted topological entropy; Heterogeneity change rate; Node importance evaluation

TP393.01

A

10.3969/j.issn.1003-6970.2017.04.014

基于粗糙概念格对城市交通科学规划研究，（JB12288）

黄加增(1974-)，男，硕士研究生，研究方向为粗糙集与概念格。

本文著录格式：黄加增. 基于复杂网络异质性的节点重要性评估方法[J]. 软件，2017，38（4）：77-84