基于离散元与有限元耦合的充气轮胎沙土路面行驶性能仿真方法研究

郑祖美， 臧孟炎， 曾海洋

(华南理工大学 机械与汽车工程学院, 广东 广州 510640)

基于离散元与有限元耦合的充气轮胎沙土路面行驶性能仿真方法研究

郑祖美， 臧孟炎， 曾海洋

(华南理工大学 机械与汽车工程学院, 广东 广州 510640)

为研究充气轮胎在沙土路面的行驶性能，提出用于模拟充气轮胎- 沙土路面行驶性能的离散元与有限元耦合模型，建立205/55R16轮胎的三维有限元模型和沙土路面离散元模型，并以离散元与有限元接触算法模拟轮胎与路面之间的相互作用。依据被动滑转原理，采用基于PID控制理论的加载方式为土槽装置轮胎加载。在自主研发的越野车沙地行驶行为仿真软件ORV-SAND中实现以上功能，仿真分析两种胎面对应轮胎的总牵引力、挂钩牵引力、行驶阻力和轮辋下陷量等行驶参数，以及不同滑转率对这些参数的影响。结果表明，仿真分析与试验结果在趋势上具有较好的一致性，说明提出的充气轮胎- 沙土路面离散元与有限元耦合模型及仿真方法在研究轮胎与沙土相互作用关系方面具有很大的潜力。

公路运输； 充气轮胎； 沙土路面； 行驶性能； 离散元与有限元耦合方法

Abstract: A combined discrete-finite element method is proposed to simulate the interaction between the pneumatic tire and the granular sand, where the continuum based finite element method is used for the pneumatic tire and the discrete element method is used for the free-flowing particles. Interactions between the pneumatic tire and the sand are described by using a contact detection algorithm. A PID-controller model based on automatic control theory is applied on the base of forced-slip principle to ascertain the loading conditions of tire. A corresponding numerical analysis code is implemented into the in-house developed code, named ORV-SAND, to simulate the tire travel performance. Travel parameters of pneumatic tires with different tread patterns (i.e. smooth and block), such as gross tractive force, drawbar pull, running resistance and sinkage, are investigated under different slip conditions. The simulated results are basically corresponded with the experimental results. It is demonstrated that the proposed discrete-finite element method and the numerical method have enormous potential in studying the interaction between the pneumatic tire and the granular sand.

Key words: highway transportation; pneumatic tire; granular sand; travel performance; discrete-finite element method

0 引言

充气轮胎与沙土路面的相互作用对越野汽车沙土路面的行驶性能有着重要影响。截止目前，试验方法是越野汽车行驶性能评价的主要方式。然而，试验方法周期长、成本高，不利于提高设计开发效率。近年来，随着计算机技术的发展，越来越多的学者采用数值仿真方法研究轮胎与路面的相互作用。常用的数值仿真方法包括有限元法、离散元法和离散元与有限元耦合的方法等。ABAQUS作为专业的有限元分析软件，广泛应用在车轮与路面相互作用问题中[1-4]。此时松软的沙土路面亦采用有限元方法模拟，并遵守相应的Druck-Prager准则或者Mohr-Coulomb准则。尽管有限元方法能够准确地模拟轮胎变形且具有较高的计算效率，但是它不能模拟车轮行驶过程中颗粒的飞溅。为了描述轮胎- 路面相互作用时沙土路面的流动和变形，很多学者采用了离散元法[5-8]。该方法中，轮胎由具有确定位置关系的离散单元组成，且通过改变离散单元之间的位置关系来模拟不同结构的轮胎，路面由离散元颗粒构成。张锐等[9-10]采用离散元商业软件PFC3D仿真了越沙步行轮在松软路面的行驶性能，并研究了轮面曲率半径对沙地刚性轮沉陷性能的影响。然而，离散单元虽然能够再现车轮行驶时的颗粒流动，却难以准确描述轮胎结构、反映轮胎的变形情况。

离散元与有限元耦合方法作为上述两种方法的结合，采用有限元法模拟轮胎变形，采用离散元法模拟沙土路面流动，采用离散元与有限元耦合接触算法模拟轮胎和沙地的相互作用，充分利用了两种方法的优点。Nakashima等[11-14]首先采用二维离散元与有限元耦合方法(DEM-FEM)对刚性车轮沙地行驶行为进行了仿真分析，并开发了相应的计算程序，随后又改进了加载方式，仿真分析了星球探测车用弹性车轮在火星土壤上的行驶性能。但是二维仿真不能处理轮胎的侧向力等问题。Michael等[15]开发了高效的离散元和有限元接触算法，最先实现了基于三维DEM-FEM的充气轮胎沙土路面行驶性能仿真分析。Zhao等[16]基于自主开发的三维DEM-FEM软件ORV-SAND，分析了不同滑转率下刚性车轮的沙地行驶行为。ORV-SAND是一款基于FORTRAN 90/95语言、具有完全自主知识产权、离散元与有限元耦合的求解工具，已获得中国版权保护中心颁发的软件著作权证书。该求解器包含了适用于处理沙地流动问题的离散元计算模块，适用于计算充气轮胎变形问题的有限元模块和适用于处理轮胎与沙地颗粒接触问题的离散元与有限元耦合模块。本文在文献[16]的基础上开发了轮胎橡胶用Mooney-Rivlin材料模型，依据室内土槽试验，建立了充气轮胎沙土路面行驶的DEM-FEM模型，采用基于PID控制的加载方式，分析不同滑转率下不同胎面结构的行驶性能，并将仿真结果与试验结果进行对比，以验证仿真分析方法的有效性。

1 轮胎- 沙土路面DEM-FEM模型

1.1 沙土路面离散元模型

图1 沙土路面离散元模型Fig.1 Discrete element model of granular sand

土槽的尺寸设置为1 500 mm×500 mm×200 mm. 本文采用球形离散单元模拟沙粒。受计算条件限制，沙粒的半径定义在5～7 mm之间，沙地离散元模型通过前处理软件生成，并在重力作用下压实[17]。图1为重力压实后的沙地离散元模型，沙粒数目为90 905.

1.2 充气轮胎有限元模型

如图2所示，将205/55R16轮胎模型简化为只包含胎面、胎侧、胎体和轮辋4部分的简易轮胎模型。其中，胎面、胎侧和胎体部分使用Mooney-Rivlin材料模拟，轮辋设为刚体。本文考虑两种胎面结构的轮胎，分别为光面轮胎(见图2(a))和块状花纹轮胎(见图2(b))。轮胎使用线性六面体有限单元描述。

图2 充气轮胎有限元模型Fig.2 Finite element model of pneumatic tire

该款轮胎在0.2 MPa内压的自由滚动半径约为317 mm，断面宽度为200 mm. 将充气轮胎放置到压实之后的沙土路面上，最终生成的DEM-FEM模型(以块状花纹轮胎为例)如图3所示。

图3 充气轮胎沙土路面DEM-FEM模型Fig.3 DEM-FEM model of pneumatic tire and granular sand

2 基于PID理论的加载方式

2.1 土槽试验

本文土槽试验采用Shinone等[18]的装置。图4和图5分别为土槽试验装置的照片和示意图，该装置采用被动滑转方法测试轮胎在沙土路面的行驶性能。

图4 试验装置照片Fig.4 Experimental set-up

图5 单轮测试系统示意图Fig.5 Schematic diagram of single wheel tester

如图4所示，试验装置主要包括土槽和单轮测试系统，单轮测试系统用于测试轮胎的沙地行驶性能。

单轮测试系统包括图5所示的行驶单元和支撑单元两部分。轮胎安装在行驶单元的驱动轴上，驱动轴通过正时皮带与电机输出轴(见图4中的电机1)相连，该电机控制轮胎的转动，轮胎转矩由安装在驱动轴上的传感器测得。当轮胎与地面接触时，会使行驶单元沿水平方向向前行驶。支撑单元由土槽端部的电机(见图4中的电机2)带动，可沿水平方向行驶。支撑单元与行驶单元之间由两个平行安装的垂直滑块连接，使行驶单元可通过滑块自由上下移动，滑块处装有两个环形称重传感器，用来测量它们之间的水平作用力(即挂钩牵引力)。

试验时，支撑单元的速度由电机2确定，是固定值。行驶单元的速度由电机1的输出转矩、挂钩牵引力和地面行驶阻力共同决定。地面行驶阻力是随时间变化的，故行驶单元的速度是随时间变化的。行驶单元速度的变化会改变支撑单元与行驶单元之间挂钩牵引力的大小，而挂钩牵引力反过来又会影响行驶单元的速度。当行驶单元速度大于支撑单元速度时，挂钩牵引力会降低行驶单元的速度；当行驶单元速度小于支撑单元速度时，挂钩牵引力会增加行驶单元的速度。故行驶单元的速度不仅随时间变化，还围绕着支撑单元的速度上下波动。保持轮胎的转动角速度不变，改变支撑单元的水平行驶速度，即可实现滑转率控制。

2.2 加载方式

为了真实地反映试验过程中轮胎与沙地的相互作用，本文采用PID控制加载方式[14]再现单个轮胎在土槽中的实际运动过程。

如图6所示，假设在固定滑转率s下，车轮的转动角速度为ω，沿x轴正方向的水平行驶速度为v. 需对轮胎加载的水平方向的力F可表示为

(1)

该式进一步可写为

(2)

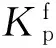
图6 挂钩牵引力计算示意图Fig.6 Schematic diagram of drawbar pull calculation

同样地，如图7所示，需对轮胎进行转矩T的加载，可表示为

(3)

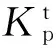
图7 转矩计算示意图Fig.7 Schematic diagram of torque calculation

此时，车轮的总牵引力Fw、挂钩牵引力Fd和行驶阻力Fr可由(4)式～(6)式表示：

(4)

Fd=-F,

(5)

Fr=-(Fw-Fd).

(6)

在此过程中，水平行驶速度与转动角速度必须满足(7)式：

(7)

式中：r为滚动半径。

3 仿真模型定义

3.1 仿真模型相关物性参数定义

仿真模型使用的各部分材料参数见表1，此时沙土路面考虑为干沙。沙土路面与充气轮胎之间的接触参数见表2. 表3给出了计算挂钩牵引力和转矩过程中用到的比例、积分和微分系数。仿真参数见文献[14,16,18]。

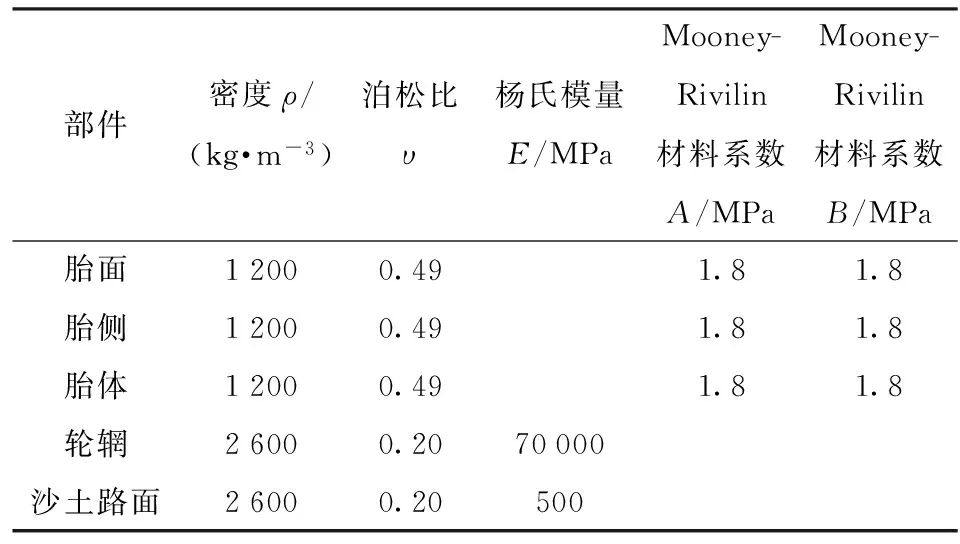
表1 充气轮胎- 沙土路面材料参数

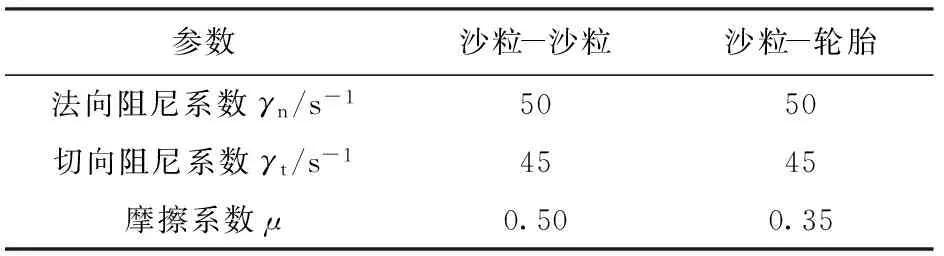
表2 充气轮胎- 沙土路面接触参数

表3 比例、积分和微分系数

3.2 仿真分析条件定义

分别计算光面轮胎和块状花纹轮胎在不同滑转率下的行驶性能，步骤如下：

1)对轮胎进行充气，充气气压为0.20 MPa，充气时间为0～10 ms；

2)对轮胎进行竖直方向载荷加载，载荷大小为980 N，加载时间为10～12 ms；

3)对轮胎进行速度加载，使其转动角速度和水平行驶速度达到预定值。轮胎的转动角速度预设值固定为0.005 rad/ms，水平行驶速度随滑转率而变化。本文中滑转率取5%、15%、25%和35%。速度加载时间为12～14 ms；

4)速度达到预定值后解除速度定义(相当于轮胎获得了初速度)，对轮胎进行挂钩牵引力和转矩加载，此后轮胎正常行驶。

轮胎与路面之间的接触算法使用自主开发的适用于处理颗粒与复杂结构接触问题的DZcell算法[19]，轮胎与沙粒之间的作用力按照Hertz-Mindlin理论[20]计算。轮胎从图3所示位置开始沿x轴正方向行驶，记录行驶速度、法向力、总牵引力、挂钩牵引力和轮辋下陷量等参数。

4 仿真结果及分析

图8给出了滑转率为5%时的轮胎转动角速度和水平行驶速度。由图8可以看出，除了加载初始时刻的波动外，轮胎的速度基本保持在预设值附近(转动角速度为0.005 rad/ms，水平行驶速度为1.5 mm/ms)，误差控制在5%以内。由此可见，本文使用的基于PID控制理论的加载方式能够使轮胎稳定行驶。

图8 滑转率为5%时轮胎的转动角速度和水平行驶速度Fig.8 Rotational and translational velocities of tire under the slip ratio of 5%

图9 充气轮胎滑转率为5%时行驶至470 ms的车辙情况Fig.9 Wheel ruts of pneumatic tires at 470 ms under the slip ratio of 5%

图9给出了两款轮胎滑转率为5%、行驶至470 ms时的行驶轨迹，云图显示了沙土路面颗粒的竖直方向位移。由图9可知：轮胎驶过的区域，沙土路面颗粒发生下陷及流动；轮胎两侧及后侧路面稍有抬升，前方路面抬升较多，这是因为轮胎行驶接近土槽边界，该区域的路面受到来自轮胎和刚性墙的共同作用，堆积现象比较明显；块状花纹轮胎驶过的区域留下了较清晰的车辙，路面下陷深度更大，这是因为带花纹的轮胎对路面的剪切作用更大。

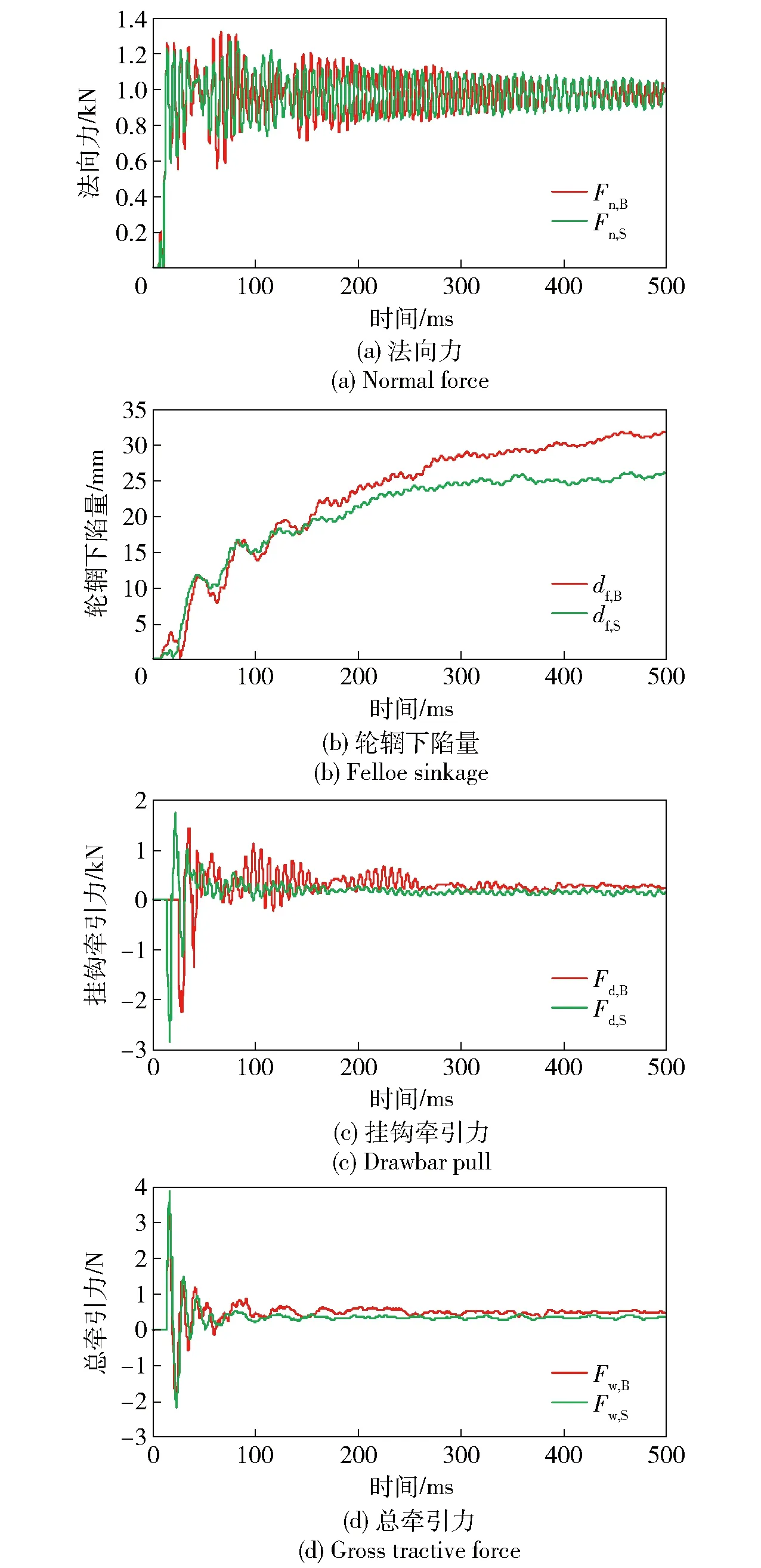
图10 充气轮胎滑转率为35%时的法向力、轮辋下陷量、挂钩牵引力和总牵引力Fig.10 Normal force, felloe sinkage, drawbar pull and gross tractive force of pneumatic tires under the slip of 35%

图10给出了两款轮胎在滑转率为35%时的法向力Fn、轮辋下陷量df、挂钩牵引力Fd和总牵引力Fw随时间变化的曲线图。图10中，B表示块状花纹轮胎，S表示光面轮胎，Fw,B即为块状花纹轮胎的总牵引力，其余以此类推。由图10可知：轮胎受力在初始时刻有较大的波动，随后逐渐稳定；两款轮胎的法向力随时间变化情况基本一致，都在980 N附近波动；花纹轮胎的总牵引力、挂钩牵引力和轮辋下陷量均大于光面轮胎。

图11和图12给出了仿真和试验[18]中不同花纹结构的轮胎行驶参数与滑转率的关系曲线。其中，图11为总牵引力、挂钩牵引力和行驶阻力随滑转率的变化趋势。图12为轮辋下陷量随滑转率的变化趋势。仿真结果取轮胎行驶到300～600 mm之间的平均值。

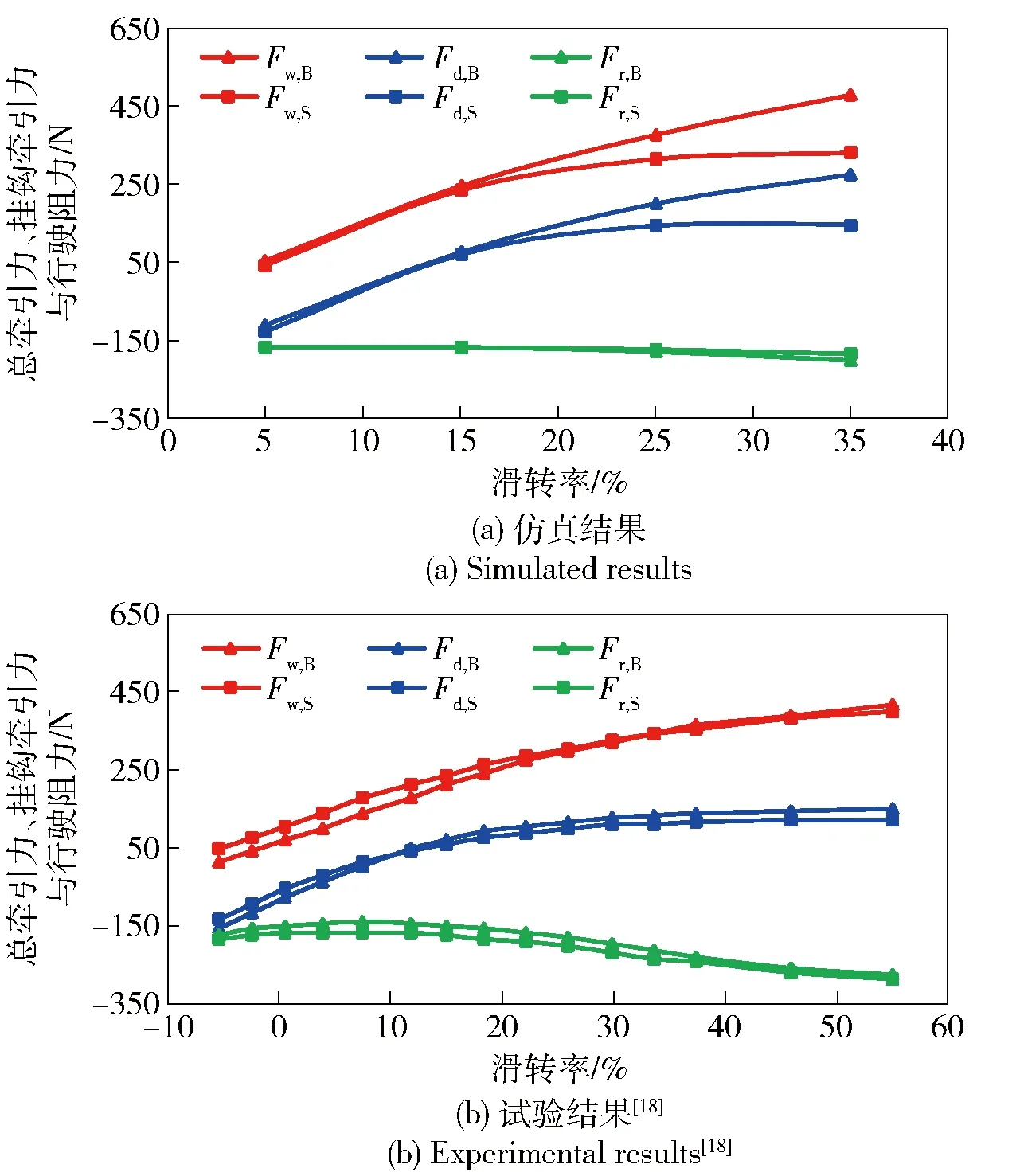
图11 总牵引力、挂钩牵引力和行驶阻力仿真结果与试验结果对比Fig.11 Comparison of simulated and experimental results: gross tractive force, drawbar pull and running resistance

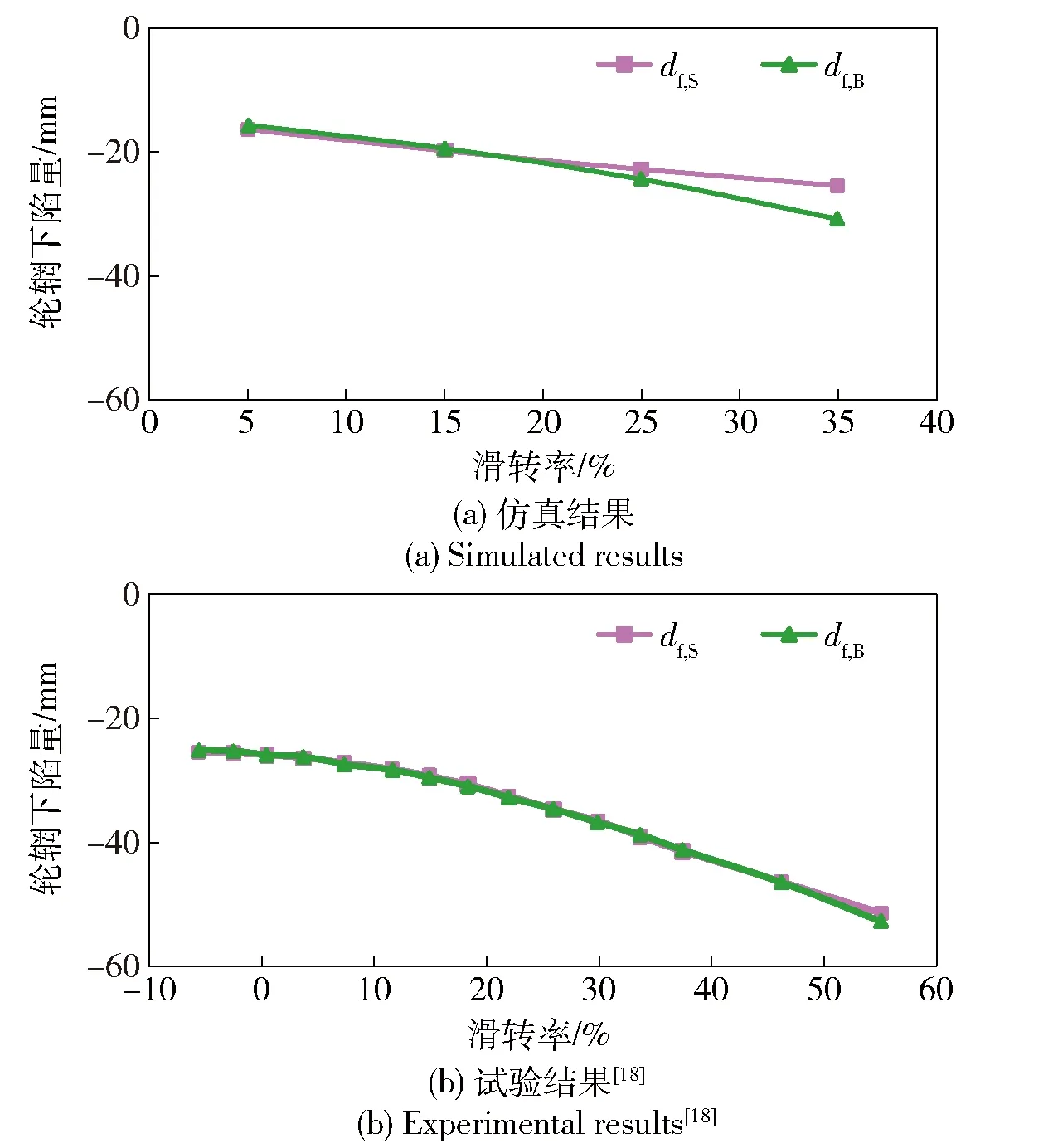
图12 轮辋下陷量仿真结果与试验结果对比Fig.12 Comparison of simulated and experimental results of felloe sinkage

由图11和图12可知：

1) 轮胎的总牵引力随着滑转率的增大单调增加。

2) 随着滑转率的增大，轮胎的挂钩牵引力增加；当滑转率大于20%时，挂钩牵引力的增长速率减小；当滑转率大于20%后，块状花纹轮胎的挂钩牵引力比光面轮胎大。

3) 当滑转率大于5%时，轮胎的行驶阻力的绝对值随着滑转率的增大而增大。

4) 轮辋下陷量随着滑转率的增加而增大。

图11、图12中仿真结果与试验结果相比，虽然二者存在一定的差别，但趋势基本一致，从而定性说明了仿真分析方法的有效性。产生差异的原因主要是沙粒大小和形状都与真实沙粒有较大的区别。后续研究将进行非球形离散单元开发，以逼真表现沙粒形状；开展分析软件的并行算法开发，使离散元颗粒逐步接近沙粒尺寸，实现轮胎沙地性能的定量评价；还会针对具体的应用，采取不同的沙地样本作相应的试验，确定仿真中需要的各项参数与实际沙地相对应。

5 结论

1)本文建立了充气轮胎沙土路面行驶性能评价的三维DEM-FEM耦合模型，采取了基于PID控制理论的加载方式，重现了室内土槽试验中轮胎的受力情况，仿真分析了不同花纹胎面结构的充气轮胎在不同滑转率下的行驶性能。

2)结果表明，随着滑转率增大，轮胎的总牵引力和挂钩牵引力都增加，但当滑转率大于20%以后，挂钩牵引力的增长率会减小。当滑转率大于20%以后，花纹轮胎的挂钩牵引力比光面轮胎大。当滑转率大于5%后，轮胎行驶阻力的绝对值随着滑转率的增加而增大。

3)尽管采用简化的充气轮胎代替真实轮胎、粒径较大的球形离散元颗粒模拟非球形沙粒，仍然得到了与试验在趋势上基本一致的仿真结果，说明了本文提出的DEM-FEM模型及仿真方法在越野车辆沙地行驶性能评价方面有很大的应用潜力。

References)

[1] 王萌. 基于软路面上车辆平顺性仿真的轮胎土壤接触模型研究[D]. 南京: 东南大学, 2009. WANG Meng. Tire-soil contact model for vehicle ride comfort simulation on soft ground[D]. Nanjing: Southeast University, 2009. (in Chinese)

[2] 任茂文, 韩卿, 张晓阳. 采用 ABAQUS/Explicit 分析滚动轮胎与变形地面相互作用[J]. 现代制造工程, 2012 (12):40-43. REN Mao-wen, HAN Qing, ZHANG Xiao-yang. The analysis on the interaction between the rolling tire and the deformed ground based on ABAQUS/Explicit[J]. Modern Manufacturing Engineering, 2012(12):40-43. (in Chinese)

[3] Li H, Schindler C. Three-dimensional finite element and analytical modelling of tyre-soil interaction[J]. Proceedings of the Institution of Mechanical Engineers Part K Journal of Multi-body Dynamics, 2013, 227(1):42-60.

[4] Cueto O G, Coronel C E I, Morfa C A R, et al. Three dimensional finite element model of soil compaction caused by agricultural tire traffic[J]. Computers & Electronics in Agriculture, 2013, 99(6):146-152.

[5] 方俊, 闫民, 许立峰. 颗粒轮胎与颗粒地面模型[J]. 科技导报, 2007, 25(24): 69-72. FANG Jun, YAN Min, XU Li-feng.Model of granule tyre and granule ground[J]. Science & Technology Review, 2007, 25(24): 69-72. (in Chinese)

[6] 叶克东. 三维 GVT 动力学模型研究[D]. 北京：北京林业大学, 2011. YE Ke-dong.Research of dynamics model of 3D GVT[D]. Beijing: Beijing Forestry University, 2011. (in Chinese)

[7] Khot L R, salokhe V M, Jayasuriya P W, et al. Experimental va-lidation of distinct element simulation for dynamic wheel-soil interaction[J]. Journal of Terramechanics, 2007, 44(6):429-437.

[8] Du Y, Gao J, Jiang L, et al. Numerical analysis of lug effects on tractive performance of off-road wheel by DEM[J]. Journal of the Brazilian Society of Mechanical Sciences & Engineering, 2016,39(6):1-11.

[9] 张锐,吉巧丽,张四华,等. 越沙步行轮仿生设计及动力学性能仿真[J]. 农业工程学报，2016,32(15):26-31. ZHANG Rui, JI Qiao-li, ZHANG Si-hua, et al. Bionic design and dynamics performance simulation of walking wheel to travel on sand[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(15): 26-31. (in Chinese)

[10] 张锐,吉巧丽,张四华,等. 轮面曲率半径对沙地刚性轮沉陷性能影响研究[J]. 农业机械学报，2016,47(11):341-349. ZHANG Rui, JI Qiao-li, ZHANG Si-hua, et al. Effect of wheel surface curvature radius on sinkage performance of sand rigid wheel[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016,47(11):341-349. (in Chinese)

[11] Nakashima H, Oida A. Algorithm and implementation of soil-tire contact analysis code based on dynamic FE-DE method[J]. Journal of Terramechanics, 2004, 41(2):127-137.

[12] Nakahima H, Takatsu Y, ShinoneH, et al. FE-DEM analysis of the effect of tread pattern on the tractive performance of tires operating on sand[J]. Journal of Mechanical Systems for Transportation & Logistics, 2009, 2(1):55-65.

[13] Ono T, Nakashima H, Shimizu H, et al. Analysis of elastic wheel performance for off-road mobile robots using FE-DEM[J]. IFAC Proceedings Volumes, 2010, 43(26): 61-66.

[14] Nishiyama K, Nakashima H, Yoshida T, et al. 2D FE-DEM analysis of tractive performance of an elastic wheel for planetary rovers[J]. Journal of Terramechanics, 2016, 64:23-35.

[15] Michael M, Vogel F, Peters B. DEM-FEM coupling simulations of the interactions between a tire tread and granular terrain[J]. Computer Methods in Applied Mechanics & Engineering, 2015, 289:227-248.

[16] Zhao C, Zang M. Analysis of rigid tire traction performance on a sandy soil by 3D finite element-discrete element method[J]. Journal of Terramechanics, 2014, 55(7):29-37.

[17] 赵春来. 基于DEM/FEM的越野车沙地行驶行为仿真评价方法研究[D]. 广州：华南理工大学, 2015. ZHAO Chun-lai. The research on the simulation evaluation method for off-road vehicle driving behavior on sand based on the DEM/FEM [D]. Guangzhou: South China University of Technology, 2015. (in Chinese)

[18] Shinone H, Nakashima H, Takatsu Y, et al. Experimental analysis of tread pattern effects on tire tractive performance on sand using an indoor traction measurement system with forced-slip mechanism[J]. Engineering in Agriculture Environment & Food, 2010, 3(2):61-66.

[19] Zheng Z, Zang M, Chen S, et al. An improved 3D DEM-FEM contact detection algorithm for the interaction simulations between particles and structures[J]. Powder Technology, 2016, 305:308-322.

AnalysisofTravelPerformanceofPneumaticTireonUnpavedRoadbyDiscrete-finiteElementMethod

ZHENG Zu-mei， ZANG Meng-yan， ZENG Hai-yang

(School of Mechanical & Automotive Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China)

U461.5+1

A

1000-1093(2017)09-1822-08

10.3969/j.issn.1000-1093.2017.09.020

2017-01-11

国家自然科学基金项目(11672344)

郑祖美(1990—), 女, 博士研究生。E-mail: z.zumei@mail.scut.edu.cn

臧孟炎(1961—), 男,教授,博士生导师。E-mail: myzang@.scut.edu.cn