弹丸在膛内运动的回波信号瞬时频率估计方法研究

王鉴, 韩焱, 王黎明, 张丕状, 陈平

(1.中北大学 信息探测与处理山西省重点实验室， 山西 太原 030051；2.中北大学 信息与通信工程学院， 山西 太原 030051)

弹丸在膛内运动的回波信号瞬时频率估计方法研究

王鉴1,2, 韩焱1,2, 王黎明1,2, 张丕状1,2, 陈平1,2

(1.中北大学 信息探测与处理山西省重点实验室， 山西 太原 030051；2.中北大学 信息与通信工程学院， 山西 太原 030051)

微波干涉仪可获取含内弹道运动信息的多普勒回波信号，为有效地估计回波信号的瞬时频率，利用短时傅里叶变换、Wigner-Ville变换、多项式调频小波变换(PCT)等方法对含有不同噪声的模拟弹丸回波信号和真实的弹丸回波信号进行分析和对比。研究结果表明：多项式调频小波构造匹配变换核的PCT方法时频聚集性最好，瞬时频率估计精度最高，并具有一定的抗干扰能力，说明PCT方法适合于弹丸在膛内运动回波信号的瞬时频率估计。

兵器科学与技术； 瞬时频率估计； 弹丸运动； 微波干涉仪； 时频分布

Abstract: The microwave interferometer can obtain the Doppler echo signal containing interior ballistic motion information. In order to estimate the instantaneous frequency of echo signal effectively, a mathematical model of motion curve of projectile in bore is established based on polynomial fitting. The methods of short-time Fourier transform, Wigner-Ville distribution, polynomial chirplet transform (PCT) are used to analyze the simulation echo signals of projectiles with different noise and experimental echo signals of projectiles, respectively. The results show that the PCT method which uses transform kernel based on polynomial frequency modulated wavelet has the best time-frequency concentration and accuracy of instantaneous frequency estimation (IFE) and good anti-interference ability compared with the other methods. The research results show that the PCT method is suitable for IFE of projectile’s signals.

Key words: ordnance science and technology； instantaneous frequency estimation； projectile motion； microwave interferometer； time-frequency distribution

0 引言

弹丸在膛内加速穿过炮膛、以一定初速离开炮口的过程中，压力、温度、初速等内弹道参数的测量对内弹道学发展有着至关重要的作用。随着科学技术发展，内弹道实验中的初速测量已经演变为弹丸在膛内速度随行程和时间变化的测量。王黎明等[1]、赵立强[2]、蔡德全[3]都对微波干涉仪的内弹道速度测量做了一定的研究。微波干涉仪建立在多普勒干涉原理的基础上，通过微波干涉产生包含弹丸运动信息的多普勒频移回波信号。弹丸的内弹道回波信号是一个非平稳信号，用时频域联合描述内弹道回波信号时，信号的能量会沿瞬时频率集中，即可以通过对信号时频峰值的估计来得到信号的瞬时频率，利用瞬时频率估计值解算出弹丸膛内速度随时间的变化关系，进而得到弹丸在膛内的加速度、行程及弹底压力等参数。在整个测量过程中，瞬时频率的估计精度决定了各参数的测量精度。

微波干涉测量系统中频率估计的方法有多种，如极值法、短时傅里叶变换(STFT)、Wigner-Ville变换(WVD)、Hilbert变换等。每种算法的频率估计精度不同，在具有不同特点的信号中为了获得较高的估计精度，通过综合多种方法进行处理或者对原有方法进行针对性的改进，使每种算法都产生了相应的改进算法并各具特点。极值法在时间上具有较高的分辨力，但是极易受到噪声的干扰，使极值点的位置产生偏差，改进后的算法[4-5]可在一定程度上降低噪声以及搜索极值点位置产生的偏差、确保频率估计的精度，在一定信噪比条件下可用，但当信号完全淹没在噪声中时，该方法的频率估计精度将无法保证。STFT是一种局部频谱分析方法，其原理是对时域信号加滑动窗口，然后对每个加窗后的信号进行傅里叶变换，能很好地分辨多分量频率成分，不会产生交叉项，但是无法同时保障时域和频域的测量精度，改进方法多采用自适应改变窗口大小或者与其他方法联合使用来弥补其不足[6-8]。WVD是信号时间自相关函数的傅里叶变换，具有良好的时间、频率分辨率和时频聚集性，是时频分析方法中应用最广的一种，但由于该方法是二次型时频分布，存在交叉项干扰。文献[9]利用WVD对去除缓变干扰后的信号进行WVD瞬时频率估计，取得了较好的结果，文献[10-11]分别采用高阶谱和多项式的方法来抑制交叉项干扰，结果表明高阶谱WVD不能有效抑制分量互交叉项的影响，多项式WVD可以消除信号非线性产生的自交叉项，但受噪声影响较大。Hilbert变换[12-15]是通过对信号进行Hilbert变换来构造解析信号，然后利用相位解卷绕实现位移测量，最后对位移结果求微分实现相应的速度测量，但其测量精度远低于多普勒测频法。Hilbert-Huang变换(HHT)是根据知名数学家Hilbert 的数学理论设计，为了分析非平稳和非线性信号的变换方法，该方法将原信号由内部模态函数分解为固有模态函数(IMF)分量，然后利用Hilbert变换得到Hilbert频谱，不需事先确定基函数，是一种更具适应性的时频局部化分析方法，能够准确地表示频率特征[16]。HHT不受Heisenberg测不准原理的制约，可以在时间和频率同时达到很高的精度，但对于弹丸在膛内运动回波信号的分析未见相关文献。随着非平稳信号时频分析的发展，时频分析方法分为非参数化时频方法与参数化时频方法[17]。非参数时频方法没有假定信号模型，对非平稳信号的时频表示往往存在集中度不高或交叉项干扰问题。参数化时频方法能够使非线性调频信号在变换域上的频谱能量分布更加集中, 有助于实现非线性调频分量的分离以及时频特征的提取[18]。弹丸在膛内运动的回波信号是非线性调频信号，可采用多项式调频信号模型[19]进行数学描述，基于这一思想，本文采用多项式调频小波构造匹配变换核对弹丸在膛内运动的回波信号进行变换，以获得较高的时频聚集性，且无交叉干扰，可保证瞬时频率估计的精度。

1 弹丸在膛内运动曲线的数学模型

内弹道方程组[20]的形状函数、燃速方程、弹丸速度与行程关系式、弹丸运动方程、内弹道基本方程如下：

(1)

(2)

(3)

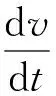
(4)

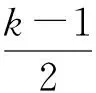
(5)

将上述方程组赋以一定的参数[20]，得到模拟的弹丸速度随时间的变化规律如图1所示。由图1可知，弹丸在膛内的运动速度随时间做非线性变化。

图1 弹丸在膛内运动速度曲线Fig.1 Velocity curve of projectile in bore

根据微波干涉仪的基本原理，多普勒频率fd和目标径向运动速度vr呈线性变化，即

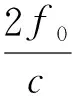
(6)

式中：f0为微波干涉仪的发射信号频率；c为发射信号传播速度，c=3×108m/s. 多普勒效应产生的回波信号的频率随时间做非线性变化。

假设微波干涉仪中心频率为94 GHz，则模拟的弹丸在膛内运动回波信号随时间变化曲线如图2所示，其中图2(a)为完整信号，图2(b)和图2(c)分别为不同时间段的局部信号。从图2中可以看出：随着时间的推移，信号幅度不随速度的改变而变化，始终保持不变；信号波形由疏变密，即瞬时频率随着时间的增加而不断增加，说明回波信号瞬时频率随速度做非线性变化，是典型的非线性调频信号。

为满足弹丸在膛内运动速度的误差要求，频率估计的精度是首要保障。本文采用一个关于时间t的N阶多项式逼近弹丸在膛内径向运动多普勒频率曲线，图3给出了4阶、5阶、6阶和8阶多项式的拟合逼近结果。从图3中可以看出，随着阶数的增加，拟合误差越来越小，计算量随之越来越大。

假设速度测量的绝对误差不大于5 m/s，则频率逼近的误差必须小于3.13 kHz. 从图3中可以看出，阶数为6时基本满足拟合精度要求，因此本文采用6阶多项式拟合逼近内弹道运动多普勒频率关于时间的曲线。

图2 弹丸在膛内运动的模拟回波信号Fig.2 Simulation echo signal of projectile in bore

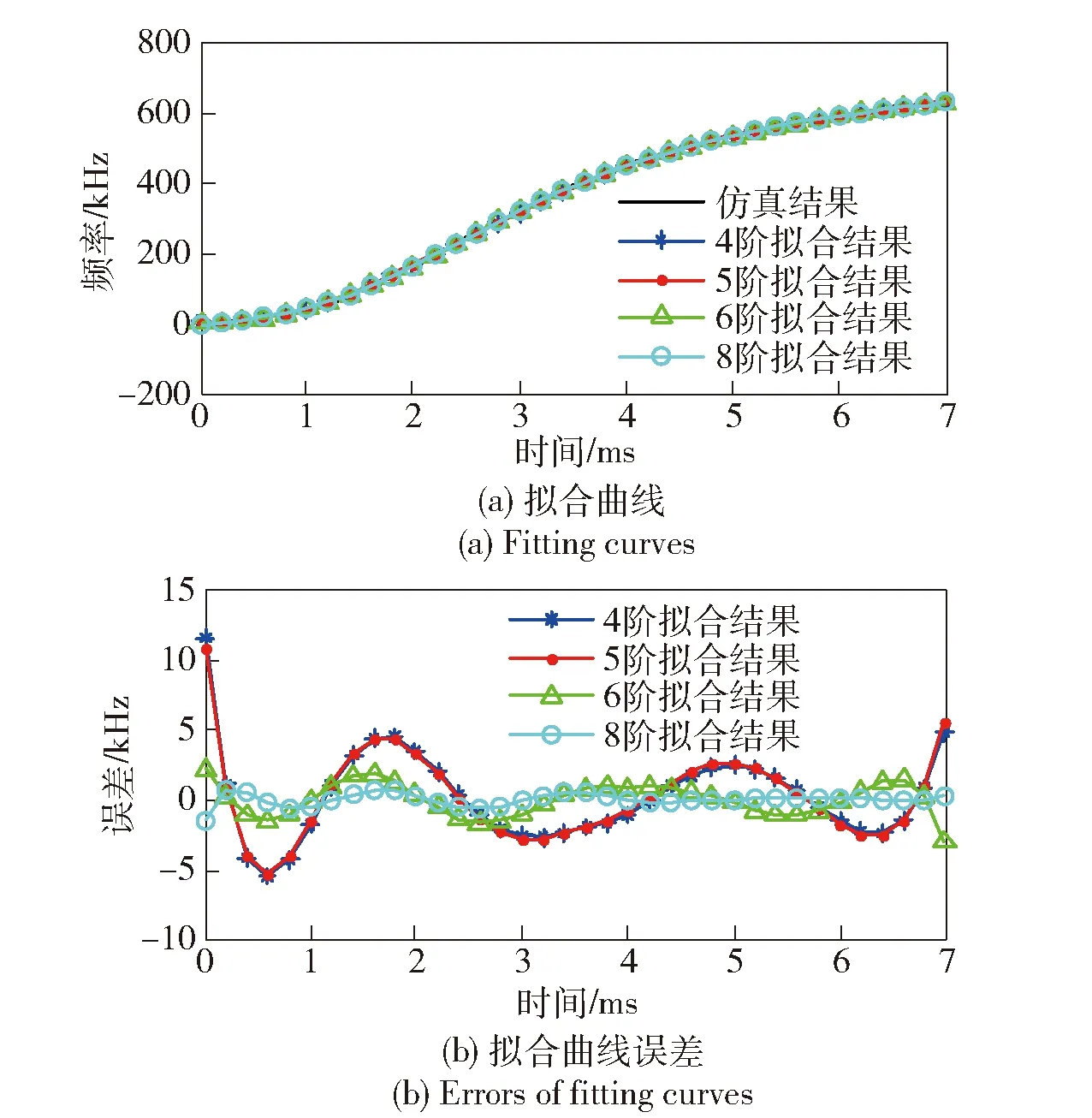
图3 不同阶数拟合逼近的频率变化曲线Fig.3 Frequency curves of different order approximations

2 瞬时频率估计原理

2.1 STFT估计原理

STFT方法是一种线性的联合时频分析方法，其实现的基本步骤如下：1)用1个窗函数来截取原始的非平稳信号，并认为该窗内的信号是平稳信号；2)将加窗后的信号进行傅里叶变换，加窗处理使得变换结果为时刻t附近很小时间段上的局部谱；3)窗函数沿着信号移动，得到信号频率随时间的变化关系，即原始信号的变换。上述处理过程中，窗函数对频谱结果有一定的影响，高斯型窗口函数由于有最小的时宽带宽积而最为常用。如果一个信号可以表示成多个信号分量的线性组合，则其时频表示也就是多个信号分量的时频表示的线性组合，从而避免了高次型非平稳分析方法中出现的交叉项干扰，可用于多分量信号分析。

对于信号x(t)，其STFT定义为

(7)

式中：g(t)为移动的窗函数；τ为窗函数的偏移量；ω为角频率；[·]*表示[·]的共轭。

2.2 WVD估计原理

WVD具有明确的物理意义，可以看作是信号时间自相关函数的傅里叶变换，解决了STFT时间分辨率、频率分辨率相互牵制的问题，是一种非常重要的非线性时频表示方法。对单分量线性调频信号具有较好的时频聚集性，但对于多分量信号，由于2次时频表示，交叉项会产生虚假信号。

对于信号x(t)，其WVD定义为

(8)

2.3 多项式调频小波变换估计原理

参数化时频方法需根据信号的模型来构造匹配的变换核。变换核参数选择的好坏，直接影响着时频能量聚集性的好坏，如果变换核和信号模型较吻合，则可取得较好的时频聚集性。弹丸在膛内的运动是一个变加速过程，运动回波信号的频率随时间做非线性变化，是典型的非线性调频信号。频率随时间变化可采用多项式拟合逼近，因此，可构造多项式调频小波变换(PCT)核来获取较好的时频聚集性。

对于信号x(t)，其PCT变换定义为

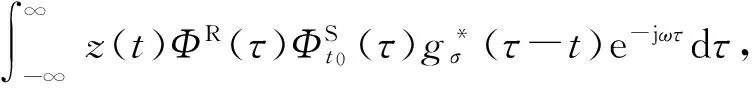
(9)

3 回波信号的瞬时频率估计

3.1 模拟回波信号的瞬时频率估计误差分析

在众多时频分析方法中，STFT 和WVD是常用的两种方法。为了对比PCT方法分析弹丸回波信号的能力，模拟的回波信号分别采用STFT、WVD、PCT方法进行瞬时频率估计。

在实际获取信号过程中，信号会受到多重干扰的影响，如缓变干扰、噪声干扰等。因此，在模拟回波信号上分别叠加缓变干扰信号、不同信噪比的噪声干扰信号进行时频分析。图4为模拟理想回波信号采用不同方法进行分析得到的时频分布图。

从图4中表示时频分布能量的颜色可以看出：PCT方法得到的脊线能量最高，主体能量区域的脊线宽度最窄，说明PCT方法的时频聚集性最好；WVD方法得到的脊线能量，时频聚集性次之，STFT方法最差；但是由于信号频率变化的非线性，WVD方法引入了自交叉干扰，这对后续的脊线提取将产生一定的影响。

图5为叠加缓变干扰的模拟回波信号采用不同时频变换方法进行分析所得到的时频分布图。

从图5中可以看出：由于多分量信号同时存在，PCT和STFT方法能很好地分辨多信号的时频特征，时频聚集性最好的依然是PCT方法；由于多分量信号的影响，WVD方法不仅有自交叉干扰还引入了互交叉干扰，交叉干扰项的能量高于信号本身的能量，使脊线提取的难度增大。从STFT方法分布图可以看出，低频缓变干扰的能量大于信号的能量，以最大能量来提取脊线，在多数时间点上会产生误差，因此实际应用中需要选用更合理的脊线提取方法。

图6、图7分别为在理想回波信号上叠加信噪比为0 dB、-10 dB的模拟回波信号，采用不同时频变换方法进行分析所得到的时频分布图。

图6和图7对比可以发现，STFT、WVD和PCT方法的时频分布均受到噪声的影响，WVD方法在信噪比为-10 dB的情况下，有效信号的能量分布曲线被噪声掩盖，而STFT方法和PCT方法具有一定的抗噪能力，脊线仍可以有效提取。在强干扰条件下，WVD方法时频分布的分析能力降低，主要原因为WVD方法是信号瞬时相关函数的傅里叶变换，在噪声较大的情况下，整体信号的相关函数主要表现为噪声的自相关函数分量，信号与噪声的互相关函数分量和信号的自相关函数相对很微弱，故无法明显地体现信号的时频特征。

图4 模拟理想回波信号时频分布图Fig.4 TFDs of simulation signals obtained by different methods

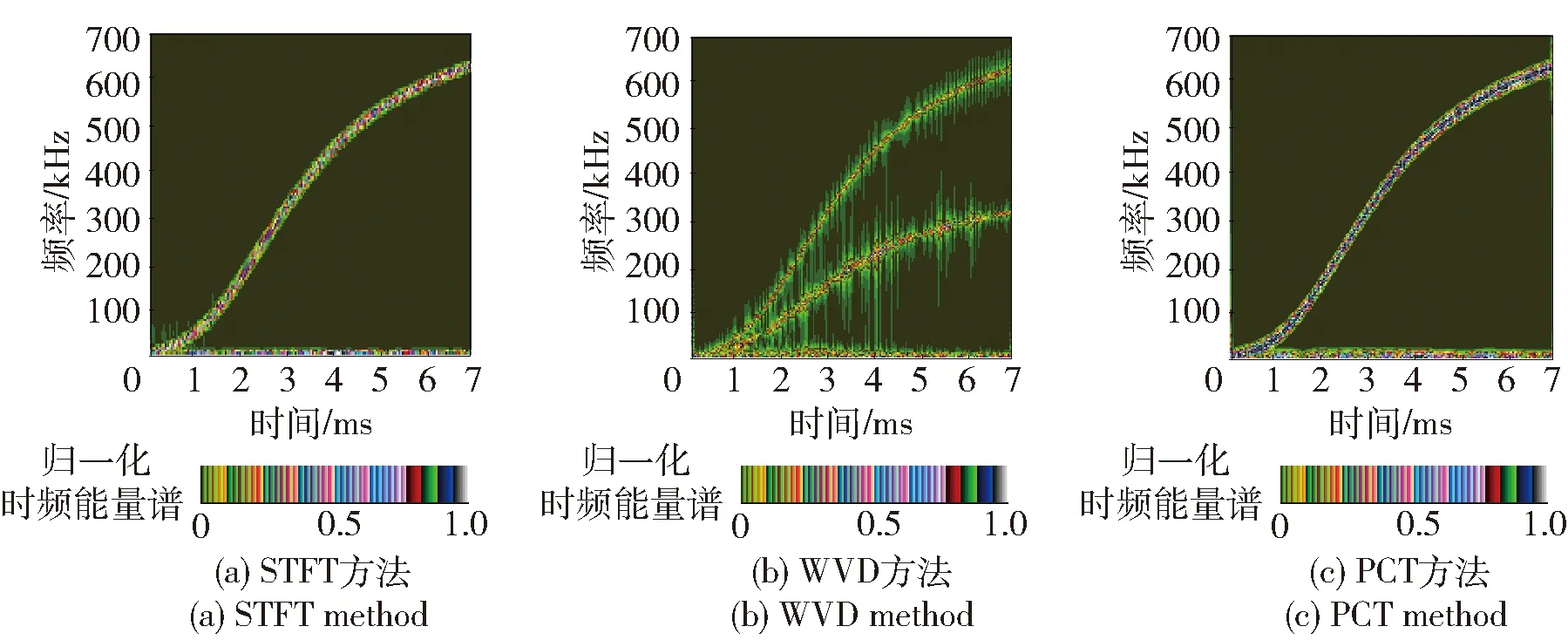
图5 叠加缓变干扰的模拟回波信号时频分布图Fig.5 TFDs of simulation signals with slow variation interference obtained by different methods

图7 叠加-10 dB噪声的模拟回波信号时频分布图Fig.7 TFDs of simulation signals with -10 dB noise obtained by different methods

图8、图9、图10分别为同时叠加信噪比10 dB、0 dB、-10 dB和缓变干扰的回波信号采用不同时频变换方法进行分析得到的时频分布图。

图8 叠加10 dB噪声和缓变干扰的模拟信号时频分布Fig.8 TFDs of simulation signals with 10 dB noise and slow variation interference

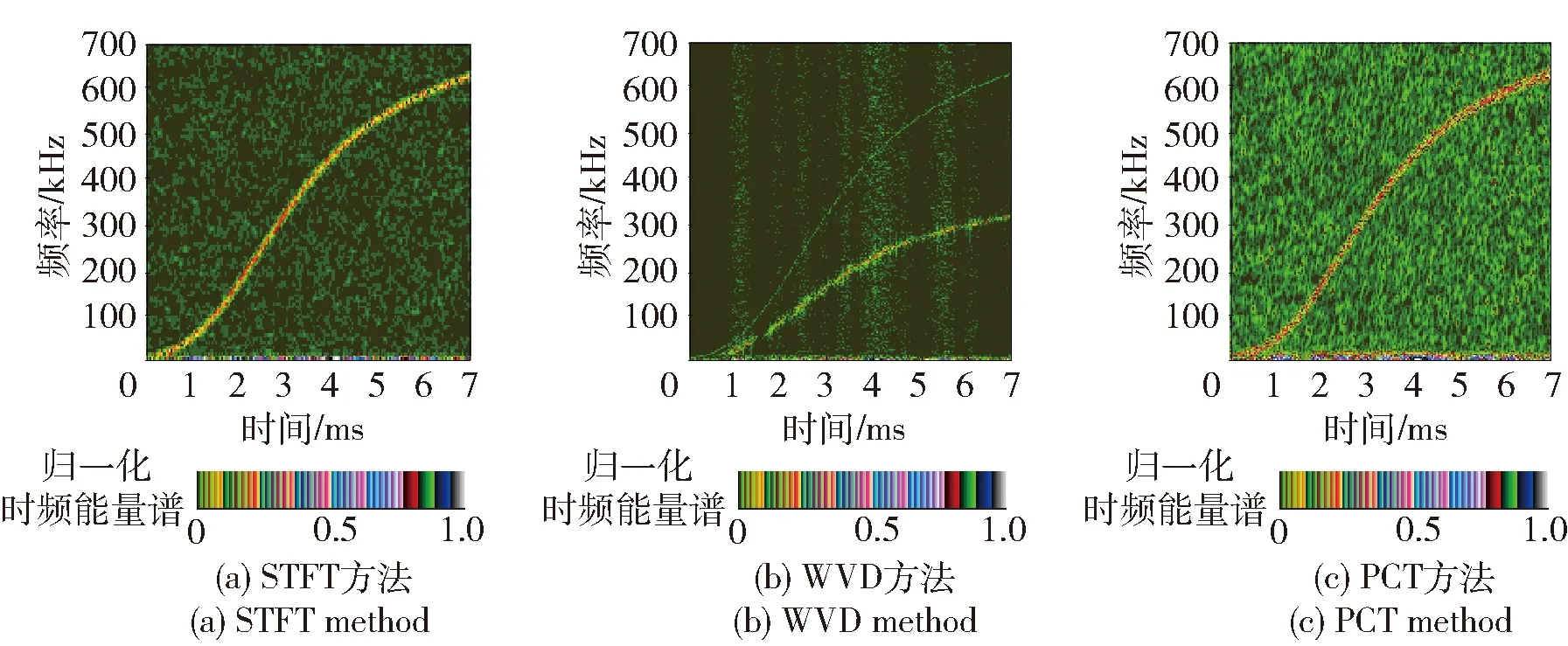
图9 叠加0 dB噪声和缓变干扰的模拟信号时频分布Fig.9 TFDs of simulation signals with 0 dB noise and slow variation interference

图10 叠加-10 dB噪声和缓变干扰的模拟信号时频分布Fig.10 TFDs of simulation signals with -10 dB noise and slow variation interference

从同时叠加不同信噪比噪声干扰和缓变干扰的信号的时频分布看，PCT方法的抗干扰能力最强，STFT方法次之，WVD方法最差，但是一定条件下WVD方法的聚集性优于STFT方法。可见选用WVD方法对含干扰的信号进行时频分析，在WVD之前必须进行预处理，以降低干扰信号的影响。

时频聚集性不仅可以通过图像直观判断，还可以用M值进行客观评价。M值定义为

(10)

式中：TFD(t,ω)为时频分布函数。M值越大，表征该时频分布聚集性越好；反之，M值越小，聚集性越差。根据(10)式，图4～图10时频分布的M值如表1所示。

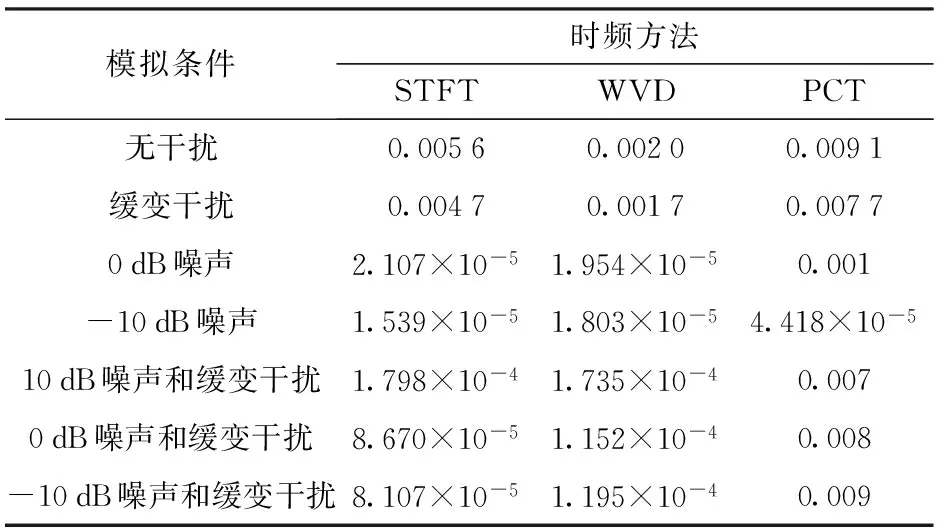
表1 不同信噪比信号3种方法时频分布的M值

由表1可以看出：PCT方法的时频聚集性优于其他两种方法；对于单一信号，噪声越大，其时频聚集性越差。对于多分量信号，M值的大小不能说明时频聚集性的好坏，必须结合图形或者其他衡量指标。

图11(a)和图11(b)分别是对图9的时频分布结果提取脊线并进行瞬时频率估计的结果。为了更好地分析3种方法提取的准确性和有效性，图11中还增加了模拟多普勒频率随时间变化的曲线。

从图11(b)可以看出：在相同脊线提取方法下，WVD方法不能正确估计瞬时频率；STFT方法在提取脊线时，在起始段脊线的部分点搜索到缓变干扰信号；总体上PCT方法得到的时频分布脊线较STFT方法和WVD方法准确，从表2的数据中也可看出PCT瞬时频率的估计精度较其余两种方法高。

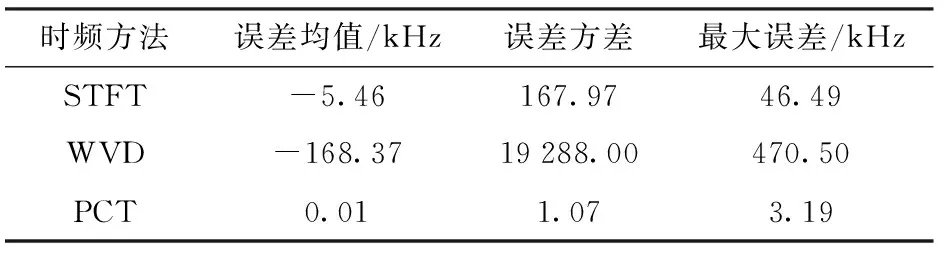
表2 不同方法瞬时频率估计精度对比

PCT方法的时间分辨率和频率分辨率较高，明显优于STFT算法，但是PCT方法的计算量庞大、运算时间长，算法必须进行一定的改进。

3.2 实际弹丸回波信号的瞬时频率估计

图12为某次实验获取的实际回波信号，图12(a)是完整信号，图12(b)和图12(c)分别是不同时段的局部信号。从图12(a)实际回波完整信号的波形图上明显看到，弹丸运动回波信号叠加在缓变干扰信号上，且幅度远远小于后者。从图12(b)和图12(c)不同时段的局部放大图中能清晰看到，弹丸在膛内运动的回波信号，由于干扰因素的影响，回波信号是幅度变化的非线性调频信号，与理想回波信号有一定差别。将图12(a)的信号未经任何预处理，分别利用STFT方法、WVD方法和PCT方法进行时频分析，可得到如图13所示的时频分布图。

图11 含干扰的模拟回波瞬时频率估计Fig.11 IFE of simulated echo signal with interference

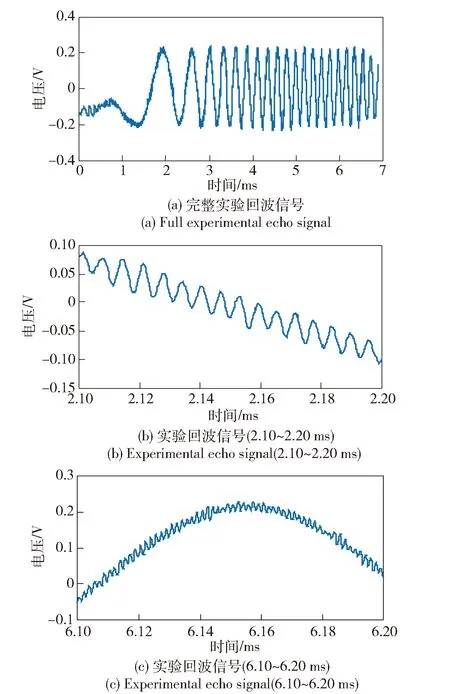
图12 实际实验获取回波信号Fig.12 Experimental echo signals of projectile in bore

图13 实际信号未经任何预处理得到的时频分布Fig.13 TFDs of experimental echo signals

根据(10)式，分别对图13中3种方法所得到的时频分布计算M值，结果如表3所示。

表3 不同方法的M值

对比M值可以看出PCT方法的时频聚集性最好。对STFT方法和PCT方法时频分布结果进行脊线提取，瞬时频率估计结果如图14所示。

图14 真实回波信号瞬时频率估计Fig.14 IFEs of experimental echo signals

从图14可以看出，STFT方法在信号末端(时间>6 ms)，频率估计的误差增加，由此可见PCT方法明显优于STFT方法。

4 结论

弹丸内弹道回波信号是一个非平稳信号，用时频域联合描述内弹道回波信号时，信号的能量会沿瞬时频率集中，即可以通过对信号时频峰值的估计得到信号的瞬时频率。本文针对含有不同噪声的模拟回波信号和真实回波信号，分别利用STFT方法、WVD方法和PCT方法实现了瞬时频率的估计，并得出以下结论：

1)PCT方法具有较强的抗干扰能力，优于STFT方法和WVD方法。

2)PCT方法的M值明显高于其他两种方法，说明其具有较高的时频分布聚集性。

3)PCT方法的瞬时频率估计精度高于STFT方法和WVD方法。

实际应用中，由于PCT方法的运算量大，算法需要进一步改进，以提高计算效率。

References)

[1] 王黎明, 赵昕, 刘洪涛, 等. 微波干涉仪测试数据处理方法[J]. 火炮发射与控制学报, 2004, 25(4):63-66. WANG Li-ming, ZHAO Xin, LIU Hong-tao, et al. Method of test data processing on microwave interferometer[J]. Gun Launch & Control Journal, 2004, 25(4):63-66. (in Chinese)

[2] 赵立强. 时频分析在内弹道测速雷达中应用[D]. 南京:南京理工大学, 2006. ZHAO Li-qiang. The application of time-frequency analysis in the interior ballistic velocity measurement radar[D]. Nanjing:Nanjing University of Science and Technology, 2006. (in Chinese)

[3] 蔡德全. 分数阶傅里叶变换在微波干涉仪中的应用[D]. 西安:西安电子科技大学, 2010. CAI De-quan. The fractional Fourier transform and its applications in microwave interferometer[D]. Xi’an: Xidian University, 2010. (in Chinese)

[4] 魏媛媛, 姚金杰. 基于小波去噪和改进极值法的动目标速度测量[J]. 微计算机信息, 2010, 26(19):217-218. WEI Yuan-yuan,YAO Jin-jie. Velocity measurement of moving target based on wavelet denoising and improved extremum method[J]. Micro Computer Information, 2010, 26(19): 217-218. (in Chinese)

[5] 刘丹, 张丕状, 马春燕. 一种精确判定多普勒信号极值点位置的方法[J]. 激光与光电子学进展, 2015, 52(7):53-57. LIU Dan, ZHANG Pi-zhuang, MA Chun-yan. A precise method to estimate location of Doppler signal’s extreme value points[J]. Laser & Optoelectronics Progress, 2015, 52(7):53-57. (in Chinese)

[6] 刘丹, 张丕状, 马春燕. 基于最小二乘法和STFT的弹丸回波信号估计分析[J]. 电子设计工程, 2015, 23(17):131-134. LIU Dan, ZHANG Pi-zhuang, MA Chun-yan. Estimates of radar echo signal and spectrum analysis based on the least square method and STFT[J]. Electronic Design Engineering , 2015, 23(17):131-134. (in Chinese)

[7] 姚金杰, 韩焱. 时频分析在变加速运动目标速度测量的应用[J]. 火力与指挥控制, 2011, 36(5):133-135. YAO Jin-jie, HAN Yan. Application of time-frequency analysis to velocity measurement of varying accelerated moving target[J]. Fire Control & Command Control, 2011, 36(5):133-135. (in Chinese)

[8] 赵彤璐, 廖桂生, 杨志伟. 基于短时迭代自适应- 逆Radon变换的微多普勒提取方法[J]. 电子学报, 2016, 44(3):505-513. ZHAO Tong-lu, LIAO Gui-sheng, YANG Zhi-wei. Micro doppler extraction based on short-time iterative adaptive approach and inverse Radon transform[J]. Acta Electronica Sinica, 2016, 44(3):505-513. (in Chinese)

[9] 姚金杰, 王黎明, 韩焱. 基于Wigner-Ville分布的毫米波测速雷达信号处理[C]∥2009年全国微波毫米波会议. 西安:中国电子学会, 2009:1421-1424. YAO Jin-jie, WANG Li-ming, HAN Yan. Signal processing of millimeter wave velocity measurement radar based on Wigner-Ville distribution[C]∥2009 National Conference on Microwave and Millimeter Waves. Xi’an:Chinese Institute of Electronics, 2009:1421-1424. (in Chinese)

[10] 陈曦, 许建中. Wigner高阶谱在弹丸膛内运动分析中的应用[J].南京理工大学学报, 2012, 36(3):442-447. CHEN Xi, XU Jian-zhong. Application of Wigner higher-order spectra in analysis of projectile motion in bore [J]. Journal of Nanjing University of Science and Technology, 2012, 36(3):442-447. (in Chinese)

[11] 杨健, 陈曦, 李学连. 基于多项式Wigner-Ville分布的膛内弹丸回波信号处理[J]. 四川兵工学报, 2012, 33(8):112-114. YANG Jian, CHEN Xi, LI Xue-lian. The processing of the echo signal of the projectile in bore based on the polynomial Wigner-Ville distribution[J]. Sichuan Acta Armamentarii, 2012, 33(8):112-114. (in Chinese)

[12] 陈征祥, 施力琳. 基于LabVIEW的微波干涉仪数据处理系统的开发[J]. 科技咨讯, 2007(24):6. CHEN Zheng-xiang,SHI Li-lin. Data processing system of microwave interferometer based on LabVIEW[J]. Science & Technology Information, 2007(24):6. (in Chinese)

[13] 柳斌, 肖剑, 郭亚龙, 等. 大口径火炮弹丸膛内参数测量方法研究[J]. 弹箭与制导学报, 2010, 30(1):167-169. LIU Bin, XIAO Jian, GUO Ya-long, et al. Study on testing methods of ballet's parameters in great calibre artillery[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010,30(1):167-169. (in Chinese)

[14] 孔伟, 王宝军, 张智源,等.内弹道多普勒信号处理方法[J]. 弹箭与制导学报, 2013, 33(3):143-145. KONG Wei, WANG Bao-jun, ZHANG Zhi-yuan, et al. The processing method of the interior ballistic Doppler signal[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2013, 33(3):143-145.(in Chinese)

[15] 孔伟, 肖剑, 常增田, 等. 基于相位解卷绕的膛内弹丸运动信号处理[J]. 弹箭与制导学报, 2012, 32(2):189-192. KONG Wei, XIAO Jian, CHANG Zeng-tian, et al. Processing of projectile motion signal in bore based on phase unwrapping[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 32(2):189-192．(in Chinese)

[16] Baccigalupi A, Liccardo A. The Huang Hilbert transform for evaluating the instantaneous frequency evolution of transient signals in non-linear systems[J]. Measurement, 2016,86: 1-13.

[17] 杨扬. 参数化时频分析理论、方法及其在工程信号分析中的应用[D]. 上海:上海交通大学, 2013. YANG Yang. Theory, methodology of parameterized time-frequency analysis and its application in engineering signal processing[D]. Shanghai:Shanghai Jiao Tong University, 2013. (in Chinese)

[18] 路文龙, 谢军伟, 王和明, 等. 基于多项式调频Fourier变换的信号分量提取方法[J]. 物理学报, 2016, 65(8):9-18. LU Wen-long, XIE Jun-wei, WANG He-ming, et al. Signal component extraction method based on polynomial chirp Fourier transform[J]. Acta Physica Sinica ,2016, 65(8):9-18. (in Chinese)

[19] Peng Z K, Meng G, Chu F L, et al. Polynomial chirplet transform with application to instantaneous frequency estimation[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(9): 3222-3229.

[20] 张小兵. 枪炮内弹道学[M]. 北京:北京理工大学出版社, 2014. ZHANG Xiao-bing. Interior ballistics of guns[M]. Beijing:Beijing Institute of Technology Press, 2014. (in Chinese)

EstimationMethodforInstantaneousFrequencyofEchoSignalofProjectileinBore

WANG Jian1,2, HAN Yan1,2, WANG Li-ming1,2, ZHANG Pi-zhuang1,2, CHEN Ping1,2

(1.Key Laboratory of Information Detection and Processing, North University of China, Taiyuan 030051, Shanxi, China;2.School of Information & Communication Engineering, North University of China, Taiyuan 030051, Shanxi, China)

TJ012.1+6

A

1000-1093(2017)09-1806-09

10.3969/j.issn.1000-1093.2017.09.018

2016-12-02

国家国防科技工业局技术基础科研项目(JCKY2014408C001)；国家自然科学基金项目(61571404、61471325、61301259、61227003)；山西省自然科学基金项目(2015021099)；山西省优秀青年学术带头人计划项目(2016年)

王鉴(1977—)，女，讲师，博士研究生。E-mail: wangblk319@163.com

韩焱(1957—)，男，教授，博士生导师。E-mail: hanyan@nuc.edu.cn