基于时间连续灰色Markov模型的维修器材需求预测方法研究

张磊， 李世民， 朱刚

(1.32134部队， 天津 301900；2.63963部队， 北京 100072； 3.78092部队， 四川 成都 610031)

基于时间连续灰色Markov模型的维修器材需求预测方法研究

张磊1， 李世民2， 朱刚3

(1.32134部队， 天津 301900；2.63963部队， 北京 100072； 3.78092部队， 四川 成都 610031)

运用时间连续且状态离散的灰色Markov过程模型，对装备维修器材的需求量进行了预测。根据装备维修器材消耗历史数据的变化幅度和数据的分布情况来划分状态区间。由各区间状态的转换情况得到Markov模型状态间的一步转移概率，论证与运用Kolmogorov微分方程求解各状态概率的时间函数并建立状态概率预测式，根据预测状态的概率值确定了灰色预测值的定位系数并求解预测值。算例分析表明，在预测维修器材需求量数据时，灰色Markov改进模型的预测精度较GM(1, 1)模型、一般灰色Markov残差修正模型以及时间离散灰色Markov链预测模型有了稳定提高，证明了该模型的有效性和实用性。

兵器科学与技术； Markov模型； 灰色预测模型； Kolmogorov微分方程； 预测精度

Abstract: The time continuous and state discrete grey Markov model is used to predict the demand of equipment maintenance materials. The state intervals are set according to the changing amplitude and distribution of consumed maintenance materials. The one-step Markov transition matrix is calculated by states transition. Kolmogorov differential equations are used to solve the time functions of state probabilities and establish the prediction equations of state probabilities. The grey positioning coefficient is determined from the probability values of predicted states. The case analysis shows that the prediction accuracy of the improved grey Markov model is higher than those of GM(1, 1) model, traditional grey Markov residual error correction model and grey Markov chain model. Its validity and practicability were proven during the prediction of equipment material demand.

Key words: ordnance science and technology; Markov model; grey prediction model; Kolmogorov differential eauation; prediction accuracy

0 引言

随着现代化武器装备功能多元性和系统复杂性的提升，其故障模式以及影响装备性能的因素也逐渐增多，故障规律极难掌握[1-3]。因此，合理预测装备维修器材的需求量，对于优化装备保障的精确性和高效性具有极其重要的意义[2-5]。

就装备维修器材的消耗情况来看，数据普遍为小样本、贫信息类型，因此灰度系统理论得到了广泛使用[6]。同时，虽然影响激励装备维修器材消耗量的因素繁多、作用机理复杂，造成器材消耗数据变化幅度较大且规律性不强，但数据变化所呈现出的随机性、无后效性特点非常适用于Markov模型[7]。因此近年来很多学者采用灰色系统理论和Markov组合模型对器材消耗量的预测问题进行了研究[4-5]。比较普遍的做法是首先采用灰色模型(GM)对数据进行拟合，根据残差值的分布情况来划分状态区间并确定Markov状态转移矩阵和初始概率分布，最后根据Markov模型的预测结果确定修正值，并对GM的预测值进行修正，以提高GM的预测精确度[4-5,8-11]。

但是，当拟合、预测的数据趋势较弱时，运用GM所得到的预测值与真实值间会产生较大幅度的偏差，仅仅对残差进行修正的效果会相当有限。同时，在历史数据有限的情况下，完全利用统计样本数确定的概率作为状态转移概率并计算不同步长的转移概率矩阵，会使计算误差不断叠加。针对这些问题，本文首先根据维修器材消耗数据变化的幅度和分布情况设计并划分了灰色状态区间。首先通过论证建立了概率统计值与转移概率强度间的关系；然后运用描述时间连续的Markov模型状态概率函数的Kolmogorov微分方程，求解得到状态概率随时间变化的函数并建立了状态概率时间预测式；最后根据各状态区间的概率结果取定了定位系数，并给出最终预测值。算例结果表明，该模型的预测精度较灰色GM(1, 1)、Markov链残差修正模型以及时间离散的灰色Markov优化模型有明显提高，证明了该模型的有效性和实用性。

1 维修器材灰数据发展趋势分析

影响装备维修器材消耗量的因素众多且彼此之间的关系不明确，因此在考虑运用灰度系统进行分析预测时应着重了解灰色系统运行机制的稳定性，评估其发展态势并预测行为特征量的发展变化。假设一维原始序列为{x(0)(k)}，k=1, 2, …,n. 序列{x(1)(k)}为序列{x(0)(k)}的一次累加序列，a为模型的发展系数，b为模型的灰色作用量。由a和b构成的灰色参数向量=[a,b]根据(1)式[7]确定：

=(BTB)-1BTY,

(1)

式中：

由(1)式确定的发展系数a反映了维修器材消耗量的发展态势。若a< 0，则说明器材消耗数量的发展态势是增长的，a的绝对值越大，相应的态势增长越快；若a>0，则说明器材消耗数量的发展态势是减小的，a越大，相应的态势减小越快。在维修器材的实际预测中，对于不同历史时间段计算出来的发展系数a，常常体现出正负交替和变化差异大等特点，说明序列{x(0)}的趋势性不强，使用GM未必能够取得理想的效果。

2 时间连续灰色Markov预测模型的建立

2.1 灰状态区间的划分

假设需要划分n个状态区间，序列{x(0)}中的最小值和最大值分别记为a1和an，则区间[a1,an]内的等间隔点可以由(2)式求得：

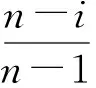
(2)

式中：i=1, 2,…,n.

⊗i=[ai-Δa,ai+Δa].

(3)

由(3)式可知，各状态区间的中点为ai,i=1,2,…,n，且状态区间划分越多，区间灰度就越小，说明历史数据越多，状态区间对于数值的变化描述就越详细。但在历史数据有限或者数据分布相对集中的情况下，划分过多的状态区间则没有意义。同时，该灰度区间越大，说明器材需求量的跳跃变化幅度越大，在小样本条件下，会造成灰度大的现象。

(3)式定义的灰数⊗i的白化值可以定义为

(4)

式中：α(t)为定位系数，0≤α(t)≤1，可视为时间的函数，可根据实际预测情况选取。

对于出现频率非常低的特殊激励点(器材需求数值突然增大或减少，但随后恢复正常的情况)，该模型则视其为发生概率极低的状态，因此其状态概率预测值会接近0，且该类数据点会位于靠近边缘的状态区间(如第1个或最后1个状态区间)内。与此同时，为降低通过概率大小选取状态区间所产生的误差风险，同时突出概率具体数值对于结果的修正作用，本文将定位系数设定为

(5)

或者

式中：αk(t)为t时刻第k个状态的区间定位系数；pi(t)为t时刻的状态概率。

2.2 预测值的残差和1步状态转移概率

预测值的残差ε(k)=x(0)(k)-(0)(k)，相对误差为

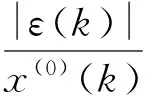
(6)

1步状态转移概率为

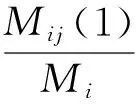
(7)

式中：Mij(1)为状态⊗i经过1步转移到状态⊗j的数据样本数；Mi为系统处于状态⊗i的数据样本数。

2.3 状态概率微分方程

由文献[6]可知，描述时间连续状态离散的Kolmogorov状态概率微分方程为

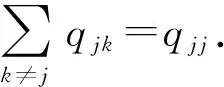
(8)

由文献[6]可知，当i≠j时，有

运用微分方程转化差分方程的思想，令Δt=1，可得

qij=pij(1).

(9)

也就是说，当i≠j时，转移强度可近似表示为对应状态的1步转移概率。

2.4 边界条件

通常情况下，方程(8)式的解为指数函数形式，由方程的形式以及状态概率分布的定义可得到第1个边界条件为

即各状态概率之和为1，式中：I为全部状态集合。同时根据预测实际，可得到第2个边界条件为

(10)

边界条件(10)式表示最后时刻的历史数据所处状态为⊗j(即n=j)的概率值为1，处于其他状态(即n≠j)的概率为0. 预测概率时视历史数据结束的时刻为初始时刻，而最后的历史数据所处状态是已经确定的，因此在初始时刻的概率值分别为1和0.

由(10)式可以看到在n个状态的条件下，会产生n+1个边界条件方程。在实际运用中，任意选择n个即可，余下的1个边界条件会自动满足。本文选择(10)式为边界条件。

3 实例分析

本文采用文献[4]中的数据作为实例，2003年～2012年的数值序列为：{x(0)}={60, 72, 81, 94, 108, 103, 95, 77, 101, 79}，利用(1)式分别计算2003年～2006年、2004年～2007年、2005年～2008年等每连续4年的GM(1, 1)发展系数a={-0.134, -0.143, -0.043, 0.063, 0.139, -0.036, -0.011}. 从中可以看出，不同时间段内的GM发展系数a呈现正负交替变化的特点，数据变化趋势性不强，因此如果运用GM(1, 1)进行预测会产生较大误差。

为了检验和比较模型的预测效果，选取前7个数据作为拟合历史数据、后3个数据作为检验对比数据，由(2)式、(3)式划分状态区间为⊗1=[48,72)，⊗2=[72,96)，⊗3=[96,120]，划分结果见表1.

由表1确定1步转移样本数矩阵为

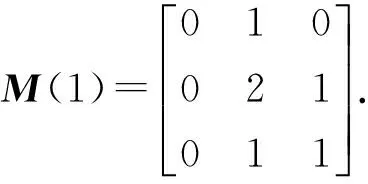
(11)

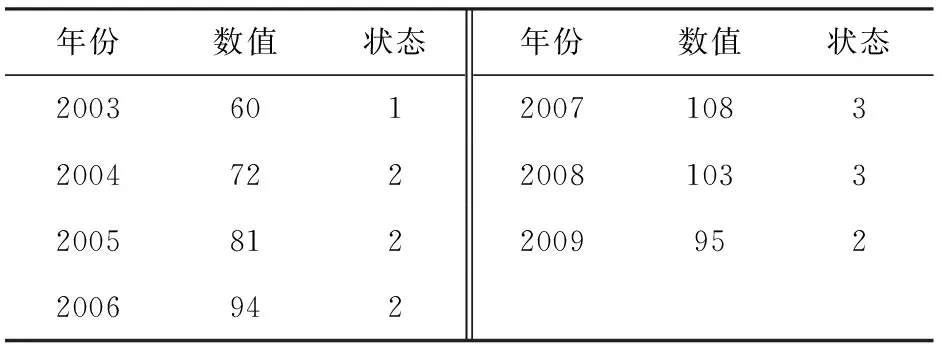
表1 状态划分结果

同时由(7)式确定1步状态转移概率矩阵为

(12)

由(9)式确定转移强度并代入(8)式，可得

(13)

由表1可知，最后时刻2009年的状态为状态2，因此由(10)式可得边界条件为

p1(0)=0，p2(0)=1，p3(0)=0.

(14)

根据边界条件(14)式求解(13)式，可得

(15)

则各状态概率的预测式为

(16)

分别令(16)式中的k取值n+1，n+2，n+3，求解未来3个时刻，即2010年、2011年和2012年的状态预测概率，通过各状态概率值的大小判断未来值所处的状态区间。显然，处于状态1的数据仅有2003年，根据历史数据判断，未来出现的可能性很低，因此状态1的预测概率为0.

由(5)式得：α(k-n)=p2(k-n)，因此有1-α(k-n)=p3(k-n).

再由(4)式可以求解最终预测值，并由(6)式计算相对误差。

为了对不同模型的结果进行对比，分别用传统GM(1, 1)、GM(1, 1)-Markov残差修正模型进行计算，其中GM(1, 1)-Markov残差修正模型在运算中同样将残差划分成3个状态区间。

同时为了检验时间连续灰色Markov模型相对于时间离散Markov模型的差别，运用时间离散Markov模型(运用(2)式、(3)式划分状态区间，(7)式确定1步状态转移概率矩阵，利用移概率矩阵的k次方确定k步转移概率矩阵并计算各时间点的状态概率，再由(4)式、(5)式求解最终预测值)。计算结果见表2.

表2 不同模型预测计算结果比较

由计算结果可以看到：由于原始数据的趋势性不强，GM(1, 1)预测值偏差较大，平均相对误差达到40.17%；Markov-GM(1, 1)残差修正模型将平均相对误差降低为32.63%，误差依然较大，因此单纯基于GM(1, 1)的残差修正没有太大意义；本文模型在这种条件下仍能保持较高的预测精度。同时，表2中时间离散和时间连续灰色Markov模型运用相同的步骤划分状态区间、确定1步状态转移概率，时间离散灰色Markov模型的平均相对误差为9.27%，时间连续灰色Markov模型将平均相对误差降低为7.77%. 说明连续时间模型能够更加准确地反映数据变化的内在机制，可以更好地避免小样本条件下运用Markov模型样本数据不足的弊端，提高预测精度。

4 结论

本文针对装备维修器材消耗量数据跳跃幅度变化较大且数据发展变化趋势不明显的情况，通过运用时间连续状态离散的灰色状态Markov模型对数据进行了分析和预测。

通过研究发现，时间连续灰色状态Markov模型可以很好地对随机变化的装备维修器材需求情况进行预测，并能够有效地避免因数据发展变化趋势不明显导致的预测偏离真实值问题。同时，该模型可以有效弥补小样本条件下运用Markov模型的不足，更好地避免误差累积并预测状态的变化规律，降低因依据状态概率大小选择预测状态所导致的高误差风险，提高运用灰度理论进行预测的精度，具有较强的实用性。

References)

[1] 马春茂,邵延君,潘宏侠,等.基于灰色马尔可夫模型的装备故障间隔期预测研究[J].兵工学报,2013,34(9):1193-1196. MA Chun-mao, SHAO Yan-jun, PAN Hong-xia,et al. TBF prediction of equipment based on the grey Markov model[J]. Acta Armamentarii, 2013, 34(9): 1193-1196. (in Chinese)

[2] 刘旭阳,吴龙涛,周万里.基于ARIMA模型的装备器材需求预测方法[J].装甲兵工程学院学报,2016,30(6):21-25. LIU Xu-yang, WU Long-tao, ZHOU Wan-li. Equipment material demand forecasting method based on ARIMA model[J]. Journal of Academy of Armored Force Engineering, 2016, 30(6): 21-25. (in Chinese)

[3] 卢庆铃,白盟亮,彭艳丽,等.基于灰色神经网络的装甲器材需求量预测[J].装甲兵工程学院学报,2011,25(6):19-22. LU Qing-ling, BAI Meng-liang, PENG Yan-li, et al. Armored equipment requirement forecasting based on grey neural network[J]. Journal of Academy of Armored Force Engineering, 2011,25(6):19-22. (in Chinese)

[4] 赵平,刘宝平,黄栋.一种用于装备维修器材消耗预测的灰色残差修正模型[J].四川兵工学报,2014,35(5):62-65. ZHAO Ping，LIU Bao-ping，HUANG Dong．Grey prediction model with residual error correction for equipment maintenance apparatus consumption prediction[J]. Journal of Sichuan Ordnance, 2014, 35(5): 62-65. (in Chinese)

[5] 王铁宁,朱域,陈晓晨.基于灰色加权马尔科夫的备件需求预测[J].装甲兵工程学院学报,2015,29(3):8-13. WANG Tie-ning, ZHU Yu, CHEN Xiao-chen. Spare parts demand forecasting based on the grey weighted Markov method[J]. Journal of Academy of Armored Force Engineering, 2015, 29(3): 8-13. (in Chinese)

[6] 刘次华.随机过程[M]. 武汉：华中科技大学出版社,2015:98-112. LIU Ci-hua. Stochastic processes[M]. Wuhan: Huazhong University of Science & Technology Press, 2015:98-112.(in Chinese)

[7] 刘思峰.灰色系统理论及其应用[M].北京:科学出版社,2014:1-15, 141-143. LIU Si-feng. Grey system theory and its application[M]. Beijing: Science Press, 2014:1-15, 141-143.(in Chinese)

[8] 赵玲,许宏科.基于改进的灰色马尔可夫链模型的交通事故预测[J].数学的实践与认识,2013,43(20):92-98. ZHAO Ling, XU Hong-ke. Traffic accident prediction based on improved grey-Markov chain model[J]. Mathematics in Practice and Theory, 2013, 43(20): 92-98.(in Chinese)

[9] 郭敏,蓝金辉,李娟娟，等.基于灰色残差GM(1,N)模型的交通数据流恢复算法[J].交通运输系统工程,2012,12(1):42-47. GUO Min, LAN Jin-hui, LI Juan-juan, et al. Traffic flow data recover algorithm based on grey residual GM(1,N) model[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(1): 42-47. (in Chinese)

[10] 王秋萍,闫海霞,闫建波.Markov残差修正的灰色GM(1,N)模型在粮食产量预测中的应用[J].西安理工大学学报,2009,25(3):347-350. WANG Qiu-ping, YAN Hai-xia, YAN Jian-bo. The application of grey GM(1,N) model with Markov residual error correction to grain yield forecasting[J]. Journal of Xi’an University of Technology, 2009, 25(3): 347-350.(in Chinese)

[11] 周浩,黄善忠.基于GM(1, 1)和灰色马尔可夫模型的器材消耗预测[J].武汉理工大学学报:交通科学与工程版,2015,39(6):1166-1168. ZHOU Hao, HUANG Shan-zhong. Equipment consumption prediction based on GM(1, 1) and gray Markov model[J]. Journal of Wuhan University of Technology :Transportation Science & Engineering, 2015, 39(6): 1166-1168. (in Chinese)

StudyofEquipmentMaterialDemandPredictionMethodBasedonTime-continuousGreyMarkovModel

ZHANG Lei1, LI Shi-min2, ZHU Gang3

(1.Unit 32134 of PLA, Tianjin 301900, China; 2.Unit 63963 of PLA, Beijing 100072, China; 3.Unit 78092 of PLA, Chengdu 610031, Sichuan, China)

E92

A

1000-1093(2017)09-1862-05

10.3969/j.issn.1000-1093.2017.09.025

2017-02-23

复杂地面系统仿真重点实验室预先研究基金项目(9140C900104150C90384)

张磊(1983—), 男, 助理工程师， 博士。E-mail: zhanglei_martin@sohu.com

李世民(1982—)，男，工程师，博士。E-mail: lishimin0625@163.com