基于拓扑优化技术的军用头盔内胆结构三维打印

姜缪文， 闫健卓， 陈继民

(1.北京工业大学 激光工程研究院， 北京 100124; 2.北京市数字化医疗3D打印工程技术中心， 北京 100124)

基于拓扑优化技术的军用头盔内胆结构三维打印

姜缪文1,2， 闫健卓2， 陈继民1,2

(1.北京工业大学 激光工程研究院， 北京 100124; 2.北京市数字化医疗3D打印工程技术中心， 北京 100124)

针对目前军用头盔的轻量化设计问题，提出基于拓扑优化技术的军用头盔内胆轻量化设计方法。利用三维(3D)打印在成型复杂异形结构时的优势，建立具有计算机建模、数值模拟、3D打印以及工程验证的军用头盔内胆结构轻量化设计流程。根据有限元分析法，提出一种基于结构势能最小的拓扑优化算法。设计流程主要包括：通过计算机辅助设计软件对设计对象进行3D建模；使用计算机辅助分析软件HyperWorks中的HyperMesh建立有限元模型；通过HyperWorks中的OptiStruct进行拓扑优化设计，查看拓扑优化模型的位移结果，确定设计结构是否满足约束条件。为满足头盔所必须具有的吸能防撞功能需求，在拓扑优化后的头盔内胆基础上，在其侧面加载蜂窝式吸能结构。使用结构优化设计软件solidThinking Inspire对带有蜂窝式结构的头盔内胆结构进行数值分析验证，模拟真实的头盔佩戴工况，优化前后的von Mises最大等效应力近似一致。对实验模型进行工程受力验证，对比优化前后军用头盔内胆的承受载荷能力。实验结果表明：在满足一定的约束条件和功能需求的情况下，拓扑优化结构可达到轻量化设计的目的，减重效果可达到17.14%，最大承受力达到原始结构的93.72%；同时3D打印技术结合数值模拟可以缩短研发周期，提高制造效率。

兵器科学与技术； 数值模拟； 三维打印； 军用头盔内胆； 拓扑优化； 蜂窝吸能结构

Abstract: A lightweight design method of military helmet liner structure based on the topology optimization technology is presented for the lightweight design of military helmet. The advantages of 3D printing in the shape of complex structures are taken to set up a lightweight design process for the helmet liner structure, in which includes the computer modeling, numerical simulation, 3D printing, and engineering verification. A topological optimization algorithm based on the minimum potential energy is summarized according to the finite element analysis method. In the design process, the computer-aided design software UG is used to perform 3D modeling for design objects, and the computer-aided analysis software HyperMesh in HyperWorks is used to build a finite element model, and view the displacement results of the topology optimization model whether the design structure meets the constraints through OptiStruct in HyperWorks for the topology optimization. In order to meet the functions of the energy absorption and anticollision, a honeycomb-type energy absorbing structure is added on the side of topologically optimized helmet liner. In experiment, solidThinking Inspire software is used to verify the helmet liner with the honeycomb structure. The simulation shows that the maximum equivalent stresses of Von-Mises before and after topology optimization are similar. The experimental model is tested, and the load capacities of helmets before and after optimization are compared. The experimental results show that, in the case of certain constraints and functional requirements, the purpose of the lightweight design can be achieved, the weight reduction can reach to 17.14%, and the maximum bearing capacity of the topologically optimized structure reaches to 93.72% of the original structure. At the same time, 3D printing technology with numerical simulation can shorten the research and development cycle, and improve manufacturing efficiency.

Key words: ordnance science and technology; numerical simulation; three-dimensional printing; military helmet liner; topology optimization; honeycomb energy absorption structure

0 引言

三维(3D)打印技术属于非传统加工工艺的范畴，涉及机电、光学、计算机、控制以及材料等多学科多领域，是全球先进制造领域的一次革新。与减材制造不同，3D打印技术可将液态聚合物、粉末等片状、丝状的离散材料逐层堆积，最终形成3D实体，可称为一次成型[1]。

3D打印技术与计算机辅助设计(CAD)、计算机辅助工程(CAE)相结合必然会带来轻量化的优势[2]。3D打印技术可实现中空夹层/薄壁加筋结构、镂空点阵结构、一体化结构、异形拓扑优化结构[3]，在结构设计层面具有轻量化的可行性。根据目前国内外研究现状[4-6]，随着UG、Hyperworks等计算机辅助软件大范围运用至工业设计中，科研人员逐渐意识到拓扑优化技术的轻量化优势。拓扑优化中的拓扑方法以边界条件、预张力和负载等条件为目标，可在一个确定的设计领域内实现材料的最佳分布，即通过拓扑优化确定和去除不影响零件刚性的材料，最终实现轻量化。

目前已有学者将计算机辅助方法运用至头盔的设计中，以提高头盔的各项性能。杨洋等[7]利用逆向动力学数值分析技术，建立了“盔- 头- 颈”模型，以计算出不同状态下肌肉激活程度的变化，在头盔的设计和使用过程中实现定量分析，提高步兵佩戴头盔时的舒适性。Erica等[8]和Edwin等[9]通过实验测量和数学模型的仿真计算，定量研究出头盔质量和质心位置变化对颈部受力的影响。Ning等[10]通过使用具有优异比强度和比模量的长纤维热塑性复合材料，用于高硬度头盔插件的加固，以提高头盔的抗冲击强度。侯宁波[11]基于人机工程学，通过对人体头部尺寸、头骨穴位进行系统的分析和研究，分析头盔内部与外部的构成要素，并从材料、功能、造型和人机工程学等相关人性化设计要素入手，实现了对军用头盔的人性化设计。宋传斌等[12]基于人体头部尺寸参数在UG中逆向生成头盔外壳，并对头盔外壳的参数化设计过程深入研究，利用UG提供的二次开发工具UG/Open定制头盔设计模块，实现了头盔外壳的全参数化设计。以上研究工作着重于头盔的舒适性、参数建模等方面，具有非常重要的指导意义。

基于复杂异形结构的轻量化设计已成为目前头盔制造的研究重点。本文采用拓扑优化技术，在结构层面对材料进行再分配，实现基于减重要求的功能最优化；以军用头盔的设计与制造为研究对象，通过拓扑优化设计实现军用头盔的轻量化；以头盔内胆的拓扑优化设计为基础，在头盔内胆的侧面设计具有吸能防撞性能的正六边形蜂窝结构，满足轻量化的同时实现头盔内胆的功能需求。本文重点研究：将3D打印的成型优势与CAD和CAE技术相结合，经过仿真分析完成头盔内胆的结构设计，实现拓扑优化后的异形结构3D打印。

1 面向军用头盔内胆设计的拓扑优化技术

军用头盔的轻量化设计在满足一定力学性能的前提下，可减轻结构质量且提高结构效率。拓扑优化技术可以满足制件结构的轻量化需求，按照设定的拓扑优化标准，将无效或低利用率的材料从结构中去除[13-15]。将军用头盔的设计结合拓扑优化技术，在结构满足刚度、强度要求的前提下，设置位移或载荷为约束，合理规划材料布局，使得结构的质量最轻。本文采用数值模拟软件Hyperworks中OptiStruct模块，对军用头盔内胆结构进行拓扑优化设计。

1.1 基于OptiStruct模块拓扑优化的结构势能最小算法

设计变量、目标函数和约束条件是拓扑优化设计的3要素。在军用头盔内胆结构设计中，将在优化过程中发生改变从而提高性能的一组参数如体积等作为设计变量；目标函数是关于设计变量的函数；约束条件是对设计变量的限制，其中约束条件可为位移约束或载荷约束。优化设计的数学模型可表述为

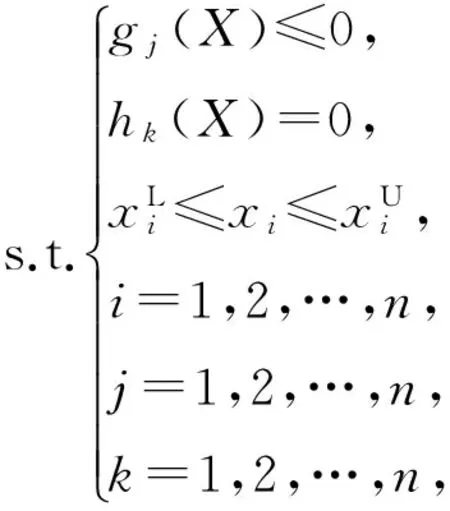
(1)

式中：X=x1,x2,…,xn是设计变量，i为设计变量的个数；f(X)是目标函数；gj(X)是不等式约束函数，j为约束的个数；hk(X)是等式约束函数，k为约束的个数；上角标L和U分别指下限和上限。

在数学模型构建之后，OptiStruct模块主要通过局部逼近的方法求解优化问题，其主要步骤可分为：

1)利用有限元分析法(FEM)对问题进行数学建模；

2)经过连续迭代计算，当目标值相差小于给定的收敛容差时，完成问题的求解收敛；

3)设计灵敏度分析，即设计响应对优化变量的偏导数；

4)根据灵敏度的设计进行近似模拟拟合，近似方法主要可分为线性模拟、倒模拟和凸模拟。

结合国内外文献关于拓扑优化的研究算法[16-18]，结构势能Π与位移δ的数学表达式为

(2)

式中：δ为边界节点位移；K为刚度矩阵；P为单元面积载荷。根据(2)式中结构势能与位移的关系，在位移约束下寻求结构势能最小，即结构的刚度最大化和位移最小化。军用头盔内胆结构的拓扑优化设计，将结构势能达到最小作为拓扑优化目标。从减伤的角度，刚度最大的头盔内胆具有最小变形能力，通过将冲击能转化为内胆结构势能的方式，减少传递到头部的冲击能量，进而保护人体的头部安全。

将结构势能最小原理运用在Optistruct模块中，通过设置体积作为设计变量，可实现拓扑优化下的体积最优化。体积优化原理可概括为：在保证军用头盔内胆结构必须满足力学性能的同时控制材料最少，以实现体积最小。结构势能最小的体积拓扑优化算法如下：

输入：军用头盔内胆结构的有限元网格模型；

输出：军用头盔内胆结构的体积最优化模型。

步骤1确定初始体积参数V0和材料允许的最大应力值σmax，计算出在施加载荷和位移约束下的最小结构势能Πmin.

步骤2开始优化体积，每优化一次体积Vi都需计算相应的结构势能Πi和相应的结构内部最大应力σimax.

步骤3当结构势能Πi下的最大应力值σimax小于材料允许的最大应力值σmax时，初始体积V0可以减小。

步骤4当结构势能Πi下的最大应力值σimax等于σmax时，体积不再减小，得到最优体积Vmin.

1.2 基于OptiStruct模块的军用头盔内胆结构拓扑优化

1.2.1 设计思想

HyperWorks软件中的Optistruct模块在结构支撑、重心优化以及实体模型内部优化等优化问题上给出了解决方案[19-21]。对于军用头盔内胆的拓扑优化设计，结合优化结果保留受力较大的区域，在不受力或者受力较小的区域采用吸能网格结构代替原有的实心结构。

在OptiStruct模块中，拓扑优化的材料模式采用密度法，即将有限元模型中设计域内每个单元的密度作为设计变量。单元密度ρ与材料弹性模量E之间具有函数关系，如图1所示。单元密度在0～1之间连续取值，优化求解后单元密度为1(或者接近1)表示该单元处的材料很重要，需要保留；单元密度为0(或者接近0)表示该单元处的材料不重要，可以去除，从而达到材料的高利用率[22]。

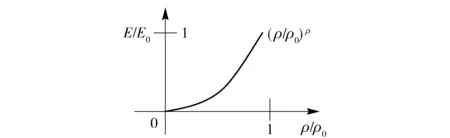
图1 单元密度与材料弹性模量的函数关系Fig.1 Relationship between the unit density and the elastic modulus of material

图2(a)的受力云图显示，U形夹具的内侧红色区域受到作用力，按照图1中ρ-E的曲线关系，图2(b)的优化结果显示：红色区域(单元密度接近1)的材料组成了传力路径，在设计中需要保留，而蓝色区域(单元密度接近0)的材料可以去除。

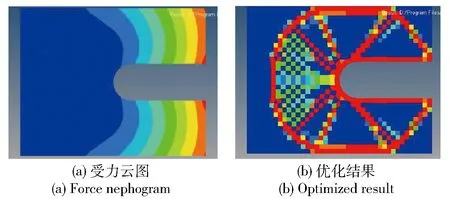
图2 拓扑优化表达形式Fig.2 Topology optimization expression

1.2.2 拓扑优化设计

以头部尺寸参数生成的二维轮廓草图为基础，通过几何约束与尺寸约束建立相关参数之间的联系，可以得到军用头盔内胆曲面的草图模型，最后通过构建拉伸、旋转和扫描等特征完成三维建模，如图3所示。

图3 军用头盔内胆三维模型Fig.3 Three-dimensional model of military helmet liner

通过UG软件设计军用头盔内胆三维模型之后，运用HyperMesh模块进行网格划分，一共形成419个节点和1 131个单元。如图4所示，在军用头盔内胆的正上方施加x、y、z3个方向的矢量力Fx、Fy、Fz，大小为1 000 N；军用头盔内胆的底部加以固定约束，约束施加位置均匀分布。

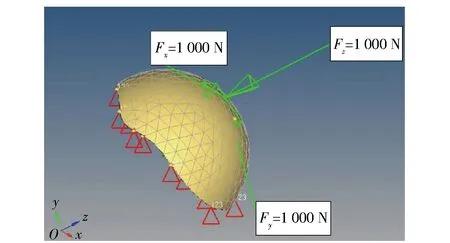
图4 军用头盔内胆有限元模型Fig.4 Finite element model of military helmet liner

由于拓扑优化中不能将应力、应变作为约束条件或目标函数，故将位移设为目标函数，拓扑优化结果显示为位移最优解(同时满足最大刚度)，即此时结构势能达到最小(由(1)式中位移与结构势能的关系可得到)。图5(a)、图5(b)、图5(c)是经过拓扑优化后，头盔模型分别在x、y和z方向上的位移云图。由图5可见，军用头盔内胆结构达到最小位移变形能力，在x方向的最大位移为9.894×10-4m，在y方向的最大位移为1.017×10-3m，在z方向的最大位移为1.116×10-3m. 经过计算，3个方向的合位移为1.805×10-3m，即经过拓扑优化后的结构势能最小。

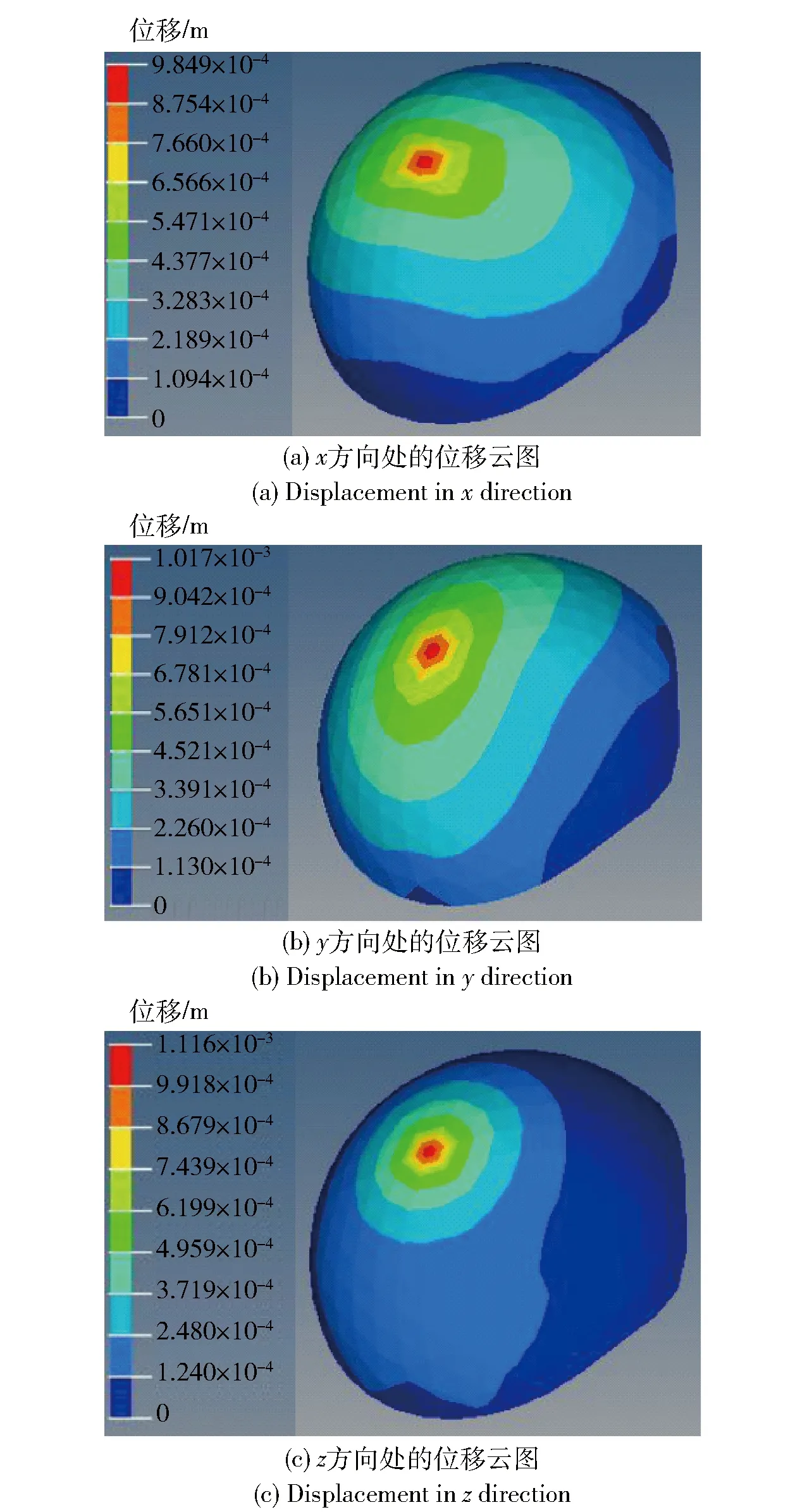
图5 位移云图Fig.5 Displacement nephogram

在OptiStruct模块中对军用头盔内胆结构进行拓扑优化，优化迭代计算25步后收敛，约束全部满足并且目标达到最小。头盔内胆顶端的最大单元密度为3.905×10-1，总体优化趋势如图6所示。

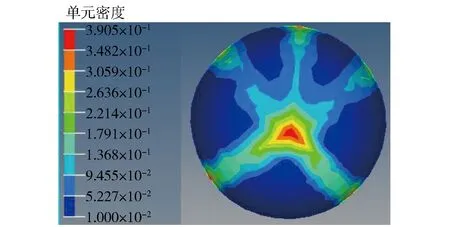
图6 拓扑优化结果Fig.6 Topologically optimized results

将单元密度极小的蓝色区域删去，得到图7所示的拓扑优化结构。由图7可见，在改变结构的同时，由受力产生的最大单元密度并未变化。

图7 拓扑优化结构Fig.7 Topologically optimized structure

2 基于吸能结构的军用头盔内胆侧面设计

2.1 设计思想

军用内胆不仅要满足一定的力学性能，更重要的是参与冲击能量的吸收，减轻外部冲击能量对人体头部的损伤。第1节对军用头盔内胆的拓扑优化设计，在实现轻量化的同时，并未满足头盔内胆缓冲吸能的功能需求。因此可在头盔的设计上加入吸能结构，以实现吸收能量防止损伤的目的。

在1.2.2节的拓扑优化设计中，设置的工况为头盔内胆顶部受集中载荷。但是军用头盔在复杂多变的战场环境下，盔体四周均有受到冲击的可能性。因此在拓扑优化设计的基础上，将吸能结构加载至头盔内胆侧面的蓝色区域(见图6)。既满足了头盔内胆在吸收能量的同时，又可对盔体的侧面加以防撞保护。

2.2 吸能结构

军用头盔碰撞的能量可通过吸能结构在碰撞过程中的塑形变形实现吸收，因此塑形变形的范围越广，头盔内胆的吸能能力越强。

多孔材料可作为理想的碰撞吸能材料。多孔材料在几何结构上的特殊性，使其在极大地提高材料抗冲击强度及抗弯能力的同时，能最大限度地减轻结构自身质量。在大多数工程应用中，单独使用多孔结构材料并不是最佳选择，而将其作为填充材料从而减轻整体结构的密度，可以最有效地发挥其优势[23-24]。结合国内外研究文献[25-27]，本文选取蜂窝式结构作为多孔吸能结构。

蜂窝式结构具有高强度比、大刚度比的性能，是理想的轻型吸能抗压结构。它由一个个六边形基本单元组成。将六边形蜂窝式结构设计在头盔内胆中，不仅不会影响拓扑优化设计带来的轻量化，还能提高头盔内胆侧面的吸能防撞能力。

利用蜂窝式结构来提高头盔内胆的侧面防撞能力，必须要考虑其力学性能。蜂窝式结构的力学性能与其所受载荷的加载方向有关[28]，图8所示为蜂窝式结构的方向性，图8中的T轴称为强轴，L轴和W轴称为弱轴。顾名思义，整个结构在强轴方向的承载能力明显大于弱轴方向，在弱轴方向的变形能力高于强轴。

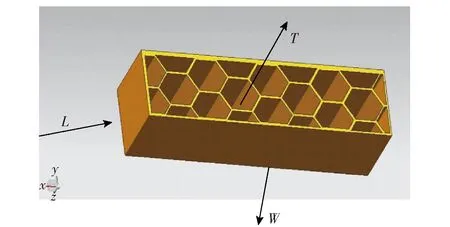
图8 蜂窝式结构方向性Fig.8 Directionality of honeycomb structure

蜂窝式结构的变形能力强，即吸能性能优越。头盔内胆侧面的法向量作为强轴，可缓冲头盔侧面的冲击力、提高头盔侧面的防撞能力；头盔内胆侧面的切向量作为弱轴，其变形能力远大于强轴方向[28]，沿着传力路径，可为头盔内胆顶部或其他方向的受力提供变形余量，减少冲击能量。结合这一特点，可在1.2.2节拓扑优化的省略区域添加正六边形蜂窝吸能结构。内胆前部区域材料较少，其目的为脸部留出空间，加载蜂窝结构的区域主要集中在中后部。结合分析优化结果，返回至UG软件中进行再设计。所设计的基于吸能结构的军用头盔内胆如图9所示。

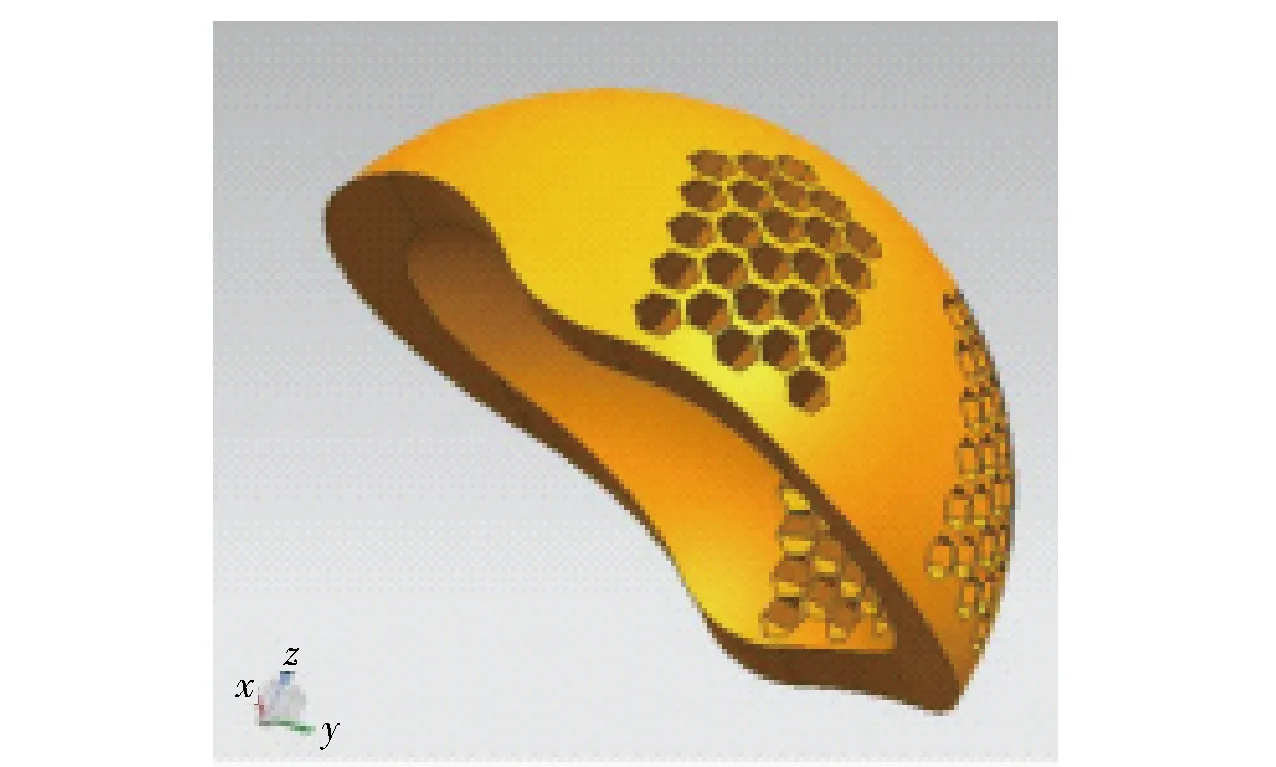
图9 基于吸能结构的军用头盔内胆Fig.9 Military helmet liner with energy absorbing structure

成型制造基于蜂窝式吸能结构的头盔内胆(见图9)，如果按照传统的机床加工模式制造，则需要经过开模、铸造、车、铣、刨和磨等复杂工序，不仅很难保证数据精确，而且会导致加工难度变大、花费时间变长。通过3D打印技术则可实现这种异形混合结构的一次成型，减少加工制造时间；如果使用精度较高的3D打印机，还可确保设计参数的准确传递。

3 实验和讨论

3.1 数值模拟验证

军用头盔在佩戴的过程中，其底部约束主要为人体头部对盔体的约束，约束加载的位置在头盔内表面且均匀分布。为了检验第2节设计的头盔内胆结构是否可靠，需要模拟真实佩戴环境对头盔内胆的影响，如图10所示。

图10 头盔内胆力学模型Fig.10 Mechanical model of helmet liner

将第2节设计完成的头盔内胆模型导入solidThinking Inspire软件中，在头盔内胆的内表面设置均匀排布的固定约束，上表面设置均匀排布的载荷(每个箭头表示100 Pa)。图11(a)和图11(b)分别表示拓扑优化结构与原始结构的受力分析。由图11可知，以von Mises等效应力作为对比参数，经过拓扑优化的头盔内胆最大等效应力为6.49×102Pa，原始结构的最大等效应力为6.443×102Pa. 由此可见，在模拟真实的头盔佩戴工况时，拓扑优化前后的von Mises最大等效应力近似一致。

图11 von Mises等效应力验证分析Fig.11 Validation of von Mises stress

3.2 工程力学验证

为方便实验，可利用控制变量法，控制拓扑优化前后内胆的尺寸一致，测试二者的质量变化和最大承载力差异。

3.2.1 3D打印模型质量测试

采用桌面型熔融沉积型3D打印机，打印材料为聚乳酸生物可降解材料，打印尺寸为80.0 mm×78.6 mm×46.8 mm，材料填充率为80%. 图12为经过拓扑优化的3D打印军用头盔内胆模型。优化前模型打印时间耗时358 min，优化后模型打印耗时323 min.

图12 3D打印模型Fig.12 3D printing model

经过质量对比，优化前模型质量为53.1 g，优化后模型质量为44.0 g，减重达到原有模型的17.14%(见图13)。

图13 质量对比Fig.13 Weight contrast

3.2.2 3D打印模型最大承载力测试

采用如图14所示的螺旋式测力实验台以及相应的数据采集软件，分别对拓扑优化前后军用头盔内胆结构3D打印模型进行力学测试。实验主要测试军用头盔内胆在拓扑优化前后两个模型破坏前的最大承受力。将军用头盔内胆底部加以固定，选择合适的压头，在军用头盔内胆上方施加稳定的垂直载荷，摇动螺旋转盘逐渐压紧被测件。

图14 螺旋式测试台Fig.14 Spiral test bench

通过与测试台配套的数据采集软件，提取数据并进行相应的误差数据筛减。图15所示为最大承载力与时间的关系，其中，黑色曲线为原始结构的承受力变化曲线，红色曲线为拓扑优化结构的承受力变化曲线。实验结果表明：经过工程力学测试，原始结构所能承受的最大破坏压力为38 886 N，拓扑优化后所能承受的最大破坏压力为36 444 N，拓扑优化结构的承载能力可达到原始结构承载力的93.72%.

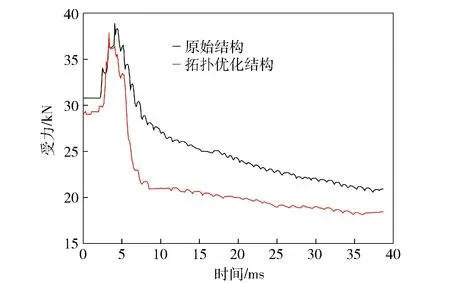
图15 最大承载力与时间关系图Fig.15 Maximum bearing capacity versus time

4 结论

本文提出了一种面向3D打印技术的军用头盔内胆结构轻量化方法，体现了具有计算机建模、数值模拟、3D打印制造以及工程验证的军用头盔内胆结构轻量化设计方法。本文的主要贡献和结论如下：

1)结合UG、HyperWorks计算机软件，充分利用CAD和CAE技术在3D打印设计过程中的优势，通过3D打印技术实现了复杂结构的一次成型，减少了加工制造时间，确保了设计参数的准确传递。

2)本文研究的基于拓扑优化设计的头盔内胆，在其内部加载蜂窝式吸能结构。将拓扑优化运用于头盔内胆设计中，在确保其一定力学性能的同时，可实现头盔内胆的轻量化，其中蜂窝结构还能对头盔起到吸能防撞缓冲的保护，满足头盔一定的功能需求。头盔内胆侧面的法向量作为强轴，可缓冲头盔侧面的冲击力，从而提高头盔侧面防撞能力；头盔内胆侧面的切向量作为弱轴，其变形能力远大于强轴方向，可为头盔内胆顶部或其他方向的受力提供变形余量，减少冲击能量。

3)实验结果表明：在满足一定约束条件的情况下，本文研究达到了轻量化设计的目的，对模型的减重效果可达到17.14%，而且拓扑优化结构的最大承受力达到原始结构的93.72%；同时3D打印技术结合数值模拟可以缩短研发周期，提高设计效率。

下一步研究将对拓扑优化算法进行优化和改进，同时提高拓扑优化模型转变成3D打印过程中的精确度。另外，可将该方法运用至一般模型的多功能设计。

References)

[1] 闫健卓, 姜缪文, 陈继民, 等. 面向光固化3D打印技术的汽车车身整体化制造及层厚优化[J]. 北京工业大学学报, 2017, 43(4): 551-556. YAN Jian-zhuo, JIANG Miao-wen, CHEN Ji-min, et al. Automobile body integration manufacturing and thickness optimization for stereo lithography 3D printing[J]. Journal of Beijing University of Technology, 2017, 43(4): 551-556. (in Chinese)

[2] 刘利刚, 徐文鹏, 王伟明,等. 3D打印中的几何计算研究进 [J]. 计算机学报, 2015, 38(6):1243-1267. LIU Li-gang, XU Wen-peng, WANG Wei-ming, et al. Survey on geometric computing in 3D printing[J]. Chinese Journal of Computers, 2015, 38(6): 1243-1267.(in Chinese)

[3] Huang X, Zhou S W, Xie Y M, et al. Topology optimization of microstructures of cellular materials and composites for macrostructures[J]. Computational Materials Science, 2013, 67:397-407.

[4] Xavier M, Novotny A A. Topological derivative-based topology optimization of structures subject to design-dependent hydrostatic pressure loading[J]. Structural and Multidisciplinary Optimization, 2017, 56: 47-57.

[5] Senhora F V, de Menezes I F M, Pereira A, et al. Topology optimization with local stress constraint on arbitrary polygonal meshes using a damage approach[J]. Revista Interdisciplinar de Pesquisa em Engenharia-RIPE, 2017, 28(2): 76-93.

[6] Zhu J H, Zhang W H, Xia L. Topology optimization in aircraft and aerospace structures design[J]. Archives of Computational Methods in Engineering, 2016, 23(4): 595-622.

[7] 杨洋, 徐诚, 管小荣,等. 基于逆向动力学的步兵头盔舒适性数值分析[J]. 兵工学报, 2015, 36(2):321-326. YANG Yang, XU Cheng, GUAN Xiao-rong, et al. Numerical analysis of comfort of military helmets based on inverse dynamics[J]. Acta Armamentarii,2015,36(2):321-326.(in Chinese)

[8] Erica D, Steve M, John B, et al. The effects of variable helmet weight and subject bracing on neck during frontal Gx impact [C]∥42nd Annual Symposium of Safe Association. Jacksonvile，US: Safe Association,2004:186-192．

[9] Edwin G P.Influence of head mass properties on head /neck during standard helicopter impact condition[C]∥60th Annual Forum of American Helicopter Society． Baltimore，MD，US: American Helicopter Society，2004:14901510.

[10] Ning H B, Pillay S, Thattaiparthasarathy K B, et al. Design and manufacturing of long fiber thermoplastic composite helmet insert[J]. Composite Structures, 2017,168:792-797.

[11] 侯宁波. 基于人性化基础上的军用头盔设计[D]. 成都：西南交通大学, 2013. HOU Ning-bo. Based on the concept of ergonomics analysis of military helmet design[D]. Chengdu：Southwest Jiaotong University, 2013.(in Chinese)

[12] 宋传斌, 张树生, 张博林. 基于UG平台的保护军用头盔外壳参数化逆向设计[J]. 现代制造工程, 2008(4):60-62. SONG Chuan-bin, ZHANG Shu-sheng, ZHANG Bo-lin. Parameterized reverse-design of the protective helmet shell based on UG-platform [J]. Modern Manufacturing Engineering , 2008(4):60-62.(in Chinese)

[13] Gardan N, Schneider A. Topological optimization of internal patterns and support in additive manufacturing[J]. Journal of Manufacturing Systems, 2014, 37:417-425.

[14] 徐文鹏, 王伟明, 李航,等. 面向3D打印体积极小的拓扑优化技术[J]. 计算机研究与发展, 2015, 52(1):38-44. XU Wen-peng, WANG Wei-ming, LI Hang, et al. Topology optimization for minimal volume in 3D printing[J]. Journal of Computer Research and Development, 2015, 52(1): 38-44.(in Chinese)

[15] Hammer V B, Olhoff N. Topology optimization of continuum structures subjected to pressure loading[J]. Structural & Multidisciplinary Optimization, 2000, 19(2):85-92.

[16] Guindon S, Gascuel O. A simple, fast, and accurate algorithm to estimate large phylogenies by maximum likelihood[J]. Systematic Biology, 2003, 52(5):696-704.

[17] Melenk J M, Babuška I. The partition of unity finite element method: basic theory and applications[J]. Computer Methods in Applied Mechanics & Engineering, 1996, 139(1/2/3/4):289-314.

[18] Sigmund O, Petersson J. Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima[J]. Structural & Multidisciplinary Optimization, 1998, 16(1):68-75.

[19] Wang S Y, Tai K, Wang M Y. An enhanced genetic algorithm for structural topology optimization[J]. International Journal for Numerical Methods in Engineering, 2010, 65(1):18-44.

[20] Hajela P, Lee E. Genetic algorithms in truss topological optimization[J]. International Journal of Solids & Structures, 1995, 32(22):3341-3357.

[21] Ma Z D, Wang H, Kikuchi N, et al. Experimental validation and prototyping of optimum designs obtained from topology optimization[J]. Structural & Multidisciplinary Optimization, 2006, 31(5):333-343.

[22] Osanov M, Guest J K. Topology optimization for architected materials design[J]. Annual Review of Materials Research, 2016, 46: 211-233.

[23] Mortazavi A, Toan V. Simultaneous size, shape, and topology optimization of truss structures using integrated particle swarm optimizer[J]. Structural and Multidisciplinary Optimization, 2016, 54(4): 715-736.

[24] 彭迎风, 辛勇. 多孔结构材料在汽车碰撞安全中的应用研究[J]. 机械设计与制造工程, 2006, 35(3):54-58. PENG Ying-feng, XIN Yong. The application of the cellular materials in automobile crash-safety[J].Machine Design and Manufacturing Engineering, 2006, 35(3):54-58.(in Chinese)

[25] Guo Z L, Teo T J, Yang G, et al. Integrating mechanism synthesis and topological optimization technique for stiffness-oriented design of a three degrees-of-freedom flexure-based parallel mechanism[J]. Precision Engineering, 2015, 39:125-133.

[26] Sun L, Gibson R F, Gordaninejad F, et al. Energy absorption capability of nanocomposites: a review[J]. Composites Science & Technology, 2009, 69(14):2392-2409.

[27] Kimura S, Mochida T, Kawasaki T, et al. Evaluation of energy absorption of crashworthy structure for railway's rolling stock (numerical simulation applying damage-mechanics model)[J]. Journal of Solid Mechanics & Materials Engineering, 2013, 7(1):102-117.

[28] 史丽萍, 赫晓东, 孟松鹤,等. MTPS金属蜂窝夹芯结构尺寸效应的数值分析[J]. 南京航空航天大学学报, 2005, 37(1):121-124. SHI Li-ping, HE Xiao-dong, MENG Song-he, et al. Numerical analysis on size effect of metal honeycomb sandwich structure in MTPS[J].Journal of Nanjing University of Aeronautics & Astronautics,2005, 37(1):121-124.(in Chinese)

3DPrintingofMilitaryHelmetLinerStructureBasedonTopologyOptimization

JIANG Miao-wen1,2, YAN Jian-zhuo2, CHEN Ji-min1,2

(1.Institute of Laser Engineering, Beijing University of Technology, Beijing 100124, China;2.Beijing Digital Medical 3D Printing Engineering Technology Center, Beijing 100124, China)

TP391.73

A

1000-1093(2017)09-1845-09

10.3969/j.issn.1000-1093.2017.09.023

2017-03-02

北京市自然科学基金项目(Z140002); 北京市科技创新项目(Z141100002814001)

姜缪文(1991—)，男，硕士研究生。E-mail：jiangmiaowen415@163.com

闫健卓(1973—)，女，副教授，博士，硕士生导师。E-mail：yanjianzhuo@bjut.edu.cn