区间二型模糊子空间0阶TSK系统*

陈俊勇，邓赵红，王士同

江南大学 数字媒体学院，江苏 无锡 214122

区间二型模糊子空间0阶TSK系统*

陈俊勇+，邓赵红，王士同

江南大学 数字媒体学院，江苏 无锡 214122

Abstract:People tend to adopt a few representative features to describe a rule,ignoring very minor,redundant information.The classical interval type-2 TSK(Takagi-Sugeno-Kang)fuzzy system adopts full data feature space at the antecedent and consequent of each rule.For high-dimensional data,it is easy to increase the complexity and reduce the interpretability.This paper proposes the interval type-2 fuzzy subspace zero-order TSK system for this problem.It uses fuzzy subspace clustering and grid partition to generate sparse and structured rule centers at the antecedent,and simplifies the consequent to be zero-order.So an interval type-2 fuzzy system using semantic more concise rules can be built.The experimental results on synthetic datasets and real datasets show that the proposed method owns good classification performance with better interpretability.

Key words:interval type-2 fuzzy system;TSK system;subspace;classification;interpretability

人们倾向于使用少量的有代表性的特征来描述一条规则，而忽略极为次要的冗余的信息。经典的区间二型TSK（Takagi-Sugeno-Kang）模糊系统，在规则前件和后件部分会使用完整的数据特征空间，对于高维数据而言，易导致系统的复杂度增加和可解释性的损失。针对于此，提出了区间二型模糊子空间0阶TSK系统。在规则前件部分，使用模糊子空间聚类和网格划分相结合的方法生成稀疏的规整的规则中心，在规则后件部分，使用简化的0阶形式，从而得到规则语义更为简洁的区间二型模糊系统。在模拟和真实数据上的实验结果表明该方法分类效果良好，可解释性更好。

区间二型模糊系统；TSK系统；子空间；分类；可解释性

1 引言

模糊推理系统（fuzzy inference system，FIS）是以模糊集合理论和模糊推理方法为基础的，具有处理模糊信息能力的系统[1]。传统的一型模糊系统得到了很多的研究，现已被成功用于智能控制等诸多领域[2-3]。近些年，二型模糊系统吸引了更多研究者的注意[4-8]。这是因为二型模糊系统采用了二型模糊集，增强了其对不确定性问题的处理能力。其中，区间二型TSK模糊系统是易于设计和实现的，同时它的IF-THEN规则是语义化的，易于理解和解释[5-8]。文献[5-8]基于KM（Karnik-Mendel）算法[9-11]，结合使用梯度下降[5,8]、支持向量回归（support vector regression，SVR）[6]、极限学习机（extreme learning machine，ELM）[7]等方法，给出了不同的区间二型TSK模糊系统或区间二型径向基函数（radial basis function，RBF）神经网络的构建方法。

在实际应用中，由于缺少专家知识，人们可能制定出冗长的多余的规则，导致模糊系统在可解释性上有所损失。常用的规则生成方法中[12]，网格划分法得到的规则易于表述，但可能产生无用的规则；聚类法控制了生成规则的数目，但可能不易描述。又在每一条模糊规则中，一般都要使用所有的输入特征，但事实上，某些特征在某条规则中的作用极其微小。选择性地排除规则中的次要信息，有助于得到稀疏后的语义简单的规则。文献[13]提出的F-ELM，实则是在一型TS系统中使用网格划分和随机法得到前件较为稀疏的规则。由于存在随机成分，F-ELM生成规则的方式具有一定的盲目性。文献[14]采用了模糊子空间聚类方法[15-16]，为规则前件的稀疏化提供可信的依据。

针对上述问题，为了得到语义简单的规则库，提高模糊系统整体的可解释性，本文提出了区间二型模糊子空间TSK（Takagi-Sugeno-Dang）系统，主要在规则前件IF部分采用了模糊子空间聚类同网格划分相结合的方法来生成规则，并简化规则后件THEN部分为0阶形式，基于KM算法，结合使用岭回归（ridge regression，RR）[17]方法来学习后件参数。

本文组织结构如下：第2章简单介绍了区间二型TSK模糊系统和模糊子空间聚类；第3章提出了区间二型模糊子空间TSK系统，详细说明了规则前件的构造和规则后件的学习；第4章为实验部分，在模拟数据集和真实的医学数据集上进行了对比实验，分析了实验结果；最后给出一般性结论。

2 相关工作

2.1 区间二型TSK模糊系统

首先，一型TSK模糊逻辑系统（TSK fuzzy logic system，TSKFLS）[2]作为模糊系统中一种经典的推理模型，因其简洁有效而被广泛应用。一型TSKFLS的模糊推理规则定义如下。

一型TSK模糊规则RULEk：

其中，IF部分为规则前件，THEN部分为规则后件；K为模糊规则条数，∧表示模糊连接符；规则前件的表示输入向量x=[x1,x2,…,xd]T的第i维特征xi所对应的第k条模糊规则的模糊子集；为规则后件参数，有时为简化规则后件，常令=0,1≤i≤d,从而得到0阶TSK模糊系统。TSKFLS的模型输出表达式如下：

其中，fk(x)表示模糊规则IF部分输出的启动强度（firing strength），可取乘法算子作为模糊连接符，按式（3）计算得到：

常取高斯关系函数：

其中,和为对应高斯关系函数的中心和标准差。

二型模糊系统使用了二型模糊集，增强集合的模糊性和处理不确定性问题的能力[4]。在各类型的二型模糊系统中，区间二型TSK模糊逻辑系统是易于设计和实现的，其常用的推理规则定义如下。

区间二型TSK模糊规则RULEk：

区别于一型TSK模糊规则，这里IF前件中使用了区间二型的模糊子集͂，并可取区间高斯关系函数：

于是，模糊规则IF部分输出的启动强度可表示为区间形式，下界和上界分别为：

Fig.1 Interval type-2 membership functions图1 区间二型关系函数

模糊规则后件THEN部分一般采用IT1型集合，而非精确值，即：

于是后件输出也是区间形式，可用左右界表示：

最后区间二型TSK模糊系统的输出为：

式（5）为一般的A2-C1形式，即前件A为二型，后件C为一型。有时也可取A2-C0或A1-C1，A2-C0采用精确值为后件参数，A1-C1则在前件中采用一型模糊集合。

2.2 KM算法

没有相关的理论可以直接求解式（11），通常要用KM算法迭代地求解出式（11）的近似结果[6-11]。KM算法存在一个规则重排的过程，重排前：

重排后的后件参数为：

Ql和Qr为K×K的矩阵，它们的每一行只有一个1，每一列只有一个1，其余元素为0，若Qr的第行的第k个元素为1，则表示将重排至位置。相应地，有。由此，区间二型TSK模糊系统的输出可以近似地表示为：

式（15a）和式（15b）中L和R是由KM算法找到的可使yl和yr接近实际值的切换点。

2.3 模糊子空间聚类

传统的K均值聚类[18]和模糊C均值（fuzzy C-means，FCM）聚类[19]默认数据的各维特征是同等重要，但这在实际应用可能并不成立。模糊子空间聚类（fuzzy subspace clustering，FSC）则充分考虑了各维特征对类簇的不同贡献程度，从而发现高维数据可能存在的特征子空间[15-16]。FSC的优化目标函数定义如下：

其中，U={ukj}K×N是硬划分矩阵，ukj表示第j个样本xj是否属于第k类簇；V={vki}K×d为K个聚类中心向量的集合；W={wki}K×d为模糊维度权重矩阵，wki表示第i维特征对第k类簇的贡献程度。

与K均值聚类方法类似，在迭代求解过程中，依据“距离”远近将不同的数据点划分到不同的类簇中（更新U），再重新计算类簇的中心（更新V）。不同的是，FSC使用了加权距离每次迭代还要计算新的权重矩阵（更新W），即：

式（16）和式（17）中，指数α＞1，通常可令α=2，ε是一个极小的正则项常数。

理论上，若类簇在某一维度的分布更为紧凑，则对应的权重分量大。删除极其次要的维度后，留下来的维度就可视为子空间。

3 区间二型模糊子空间0阶TSK系统

对于分类问题来说，在一些场景下，依据某几维特征即可判定输入数据属于某一类，也即某类数据具有明显的子空间特征。如图2所示，对于分布在第四象限的点，只需依据它们的纵坐标就可将它们同其他两类分割开来；又如香蕉独特的形状有别于苹果、梨等水果，颜色、含糖量等特征对于从中挑出香蕉这一任务则没有太大作用。这种情况在其他场景的很多应用中也是很有可能出现的。为了规则语义的明确，定义如下稀疏化的区间二型TSK模糊规则。

区间二型0阶TSK模糊子空间规则RULEk：

相比经典的区间二型TSK模糊规则，这里存在两点不同之处。其一，为了规则的简洁，后件部分已简化为C0型0阶的形式，即每条规则后件只有一个精确参数；其二，定义矩阵S=[s1,s2,…,sK]T∈RK×d,其中sk=[s(k,1),s(k,2),…,s(k,d)]∈Rd,s(k,i)∈{0,1}表示第k条规则所关心的特征子空间。s(k,i)=0时，,即表示第k条规则不关心第i个输入特征；反之，表示第k条规则使用第i个输入特征。特别的，当向量sk中的元素全为1时，前件部分就与经典的区间二型TSK模糊规则无异。

基于这样一个新的规则定义，本文提出了区间二型模糊子空间TSK系统（IT2-FS-0-TSK system），并参考文献[6-7]的方法，给了3段式构建方法，具体步骤见下文。

3.1 规则前件的构造

在缺少专家知识的情况下，通常可用网格划分或聚类的方法产生模糊规则前件。网格划分的可解释性更好，但对于高维数据，网格划分会生成数量庞大的规则，其中一些可能是无用的。减法聚类[12,20]、FCM等方法则可生成有限的规则，即可将聚类中心作为高斯关系函数的中心，但是所得到的规则的语义可能会有所损失。如图2（a），对于二维坐标系中的3类数据点，它们分别分布在第一、二、四象限，若采用网格划分法，则在第三象限对应生成了一些无意义的规则中心（图2中网格线的交点），若采用聚类方法，则规则中心（图2（a）中的圆点）不落在更具意义的点上。为保证规则的语义明确和数量有限，可以结合这两种常规方法，即通过微调将聚类所得规则中心移至最近的网格划分点，如图2（b）。

Fig.2 Grid partition and cluster centers图2 网格划分与聚类中心

同时，还要寻找模糊规则的特征子空间。文献[13]在网格划分的基础上，对规则前件做了随机的稀疏处理，使得模糊规则更为简洁。但是，由于含有随机成分，就需要多次实验来找到一组较好的稀疏化的规则前件，存在一定的盲目性。综合考量，本文采用模糊子空间聚类的方法来寻找规则中心V={vki}K×d,并按网格划分求vki的邻近点。例如，网格划分为[0,0.25,0.50,0.75,1.00]，若vki为 0.27，则取均值=0.25。给定超参数h和r：

根据FSC算法得到的权重矩阵W={wki}K×d来适当地抽取子空间特征，以此达到对规则前件进行稀疏的目的。可按式（20）选取权重大的特征：

式（20）中，0≤η＜1为超参数。

于是，按照公式定义的模糊规则，IF部分输出的启动强度可表示为区间形式，下界和上界分别为：

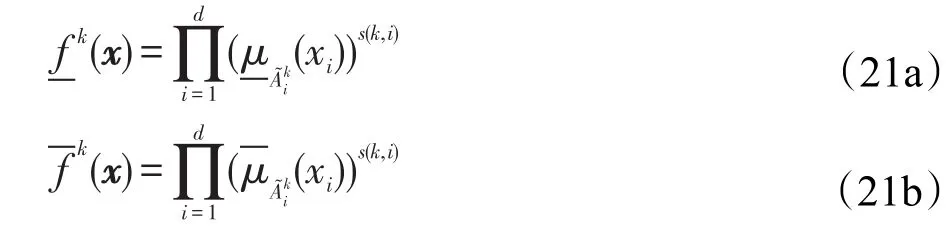
3.2 规则后件的初始化

在生成规则前件之后，先初始化规则后件。系统的输出左界和右界分别为：

最终输出结果为左右界的中间值：

可令前件参数为：

以及后件参数为：

式（23）即可写为线性形式：

对于给定的训练数据集D={xj,yj}，可以得到变换后的数据集={ϕ1(xj),yj}，可令：

按式（27）得到：

这里运用岭回归的理论[17]，待优化的目标函数为：

式（30）中λ是正则项超参数。取式（30）关于ω的导数并令其等于0，得到后件参数的最优解：

3.3 规则后件的再学习

在得到初始化的模糊规则后件参数后，即可用KM迭代算法来计算区间二型TSK模糊系统的输出结果。根据KM算法，增序排列得到重排后的后件参数，并找到切换点L和R：

其中，IM表示M×M的单位矩阵；0M表示M×M的全零矩阵。同理：

式（35）中：

对于给定的训练数据集D={xj,yj},可以得到变换后的数据集，可令：

按式（37）得到：

这里运用岭回归的理论，待优化的目标函数为：

式（41）中λ是正则项超参数。取式（41）关于ω的导数并令其等于0，得到后件参数的最优解：

4 实验研究

4.1 实验设置

本文以Matlab 8.1为实验平台，所用计算机主频3.40 GHz，内存4.00 GB，64位操作系统。用到的对比算法为核岭回归（kernel ridge regression，KRR）[21]、支持向量机（support vector machine，SVM）[22]、极限学习机（ELM）[23-24]、模糊推理系统（FIS）、基于模糊子间聚类的0阶岭回归TSK模糊系统（FSC-0-RR-TSKFS）[14]和二型模糊极限学习算法（T2FELA）[7]。其中SVM来自著名的LIBSVM[25]，FIS来自Matlab自带的工具箱，其他算法依据相关文献编程实现。

本文分别在模拟和真实数据集上进行了实验，并采用了网格参数寻优和5折交叉验证的策略。各算法参数设置及搜索网格如表1所示。最终以“均值±标准差”的形式给出分类测试精度。

Table 1 Parameter settings and search grids of different methods表1 各算法参数设置及搜索网格

4.2 模拟数据集实验

为了充分体现本文方法的意义，现构造3类、共300例的模拟数据集，每一类100例。每例数据具有12维特征，记为F1～F12。特征分布如图3所示，可见各类数据具有明显的特征子空间。A类数据在F4～F7上集中分布在[0,0.4]的范围，其余特征分布散乱；B类数据在F2～F5上集中分布在[0.35,0.65]的范围，其余特征分布散乱；C类数据在F7～F10上集中分布在[0.6,1.0]的范围，其余特征分布散乱；而F1、F11和F12完全都属于噪声。

Fig.3 Feature distribution of 3-class synthetic dataset图3 3类模拟数据的特征分布

在这样特殊的数据集上，本文方法和FSC-0-RRTSK-FS都将规则数目设为3（不依照表1对此寻优），期望的输出为[1,0,0]、[0,1,0]和[0,0,1]这3类，实验结果如表2所示。在去除噪声维时，KRR、SVM、ELM和本文方法都获得了0.97以上的分类精度，而在含有噪声时，各对比算法的分类精度受到明显影响。在η=0时，即本文方法不使用特征子空间时，其表现与ELM等算法相近；而当η＞0时，即本文方法使用特征子空间，生成稀疏规则时，其表现优于各对比算法。这说明，当分类数据具有特征子空间时，本文方法可有效排除噪声和次要特征。

表3显示了5折交叉实验中最后一折时训练所得模型参数，即产生了3条模糊规则，每条规则正好对应一类数据。例如，规则R1对应于B类，只使用了F2～F5，而忽略了其他次要特征（包括噪声）的影响，可解释为当F2～F5处于中等左右的水平时，数据属于B类的可能性为1.26。规则R3与期望的有所出入，这是因为FSC是无监督聚类，初始化时含有随机因素。FSC-0-RR-TSK-FS得到了与表3相似的稀疏规则。总体而言，对于模糊系统而言，本文方法可得到语义更为简洁的规则，可解释性更好。实际应用中，情况会复杂得多，通常需要更多的规则来构建区间二型模糊子空间0阶TSK系统。

Table 2 Classification accuracies of different methods on synthetic dataset表2 模拟数据集上各算法的分类精度

Table 3 Rules generated by the proposed method on synthetic dataset表3 本文方法在模拟数据集上生成的规则

4.3 真实数据集实验

本文用到了9个医学相关的真实数据集，涉及乳癌、心脏病、肝炎等，全部来自UCI机器学习库（http://archive.ics.uci.edu/ml/datasets.html），如表4所示。实验中，除了类标签外，所有特征都被归一化到区间[0,1]。其中一些数据集的全部特征都是连续量，而另一些则包含或全部为离散型特征。例如，年龄是连续量特征，而性别是离散型特征。

对于离散型特征，本文方法在生成模糊规则时，将FSC得到的规则中心微调至相近的特征值上；而对于连续量特征，本文方法先设该特征有[0,0.25,0.50,0.75,1.00]这5个等级，生成模糊规则时，将FSC得到的规则中心微调至相近的等级上。这样做的目的就是为了保证规则语义的清晰。例如，对于人的年龄，可将[0,0.25,0.50,0.75,1.00]解释为少年、青年、中年、中老年和老年。

实验结果如表4所示，由于真实数据集的复杂性，本文方法只在部分数据集上获得了略好于对比算法的分类精度。且当本文方法在Hepatitis等数据集上体现一定优势时，同样考虑子空间的FSC-0-RRTSK-FS也取得了相近的结果。在缺少专家知识的情况下，由此可佐证模糊子空间在构造规则前件时所能发挥的作用。

但是，特征子空间的利用不能完全保证取得更高的分类精度，相反，对于各项特征都一般重要的数据集，不恰当地排除一些不十分次要的特征，可能导致信息完整性的缺失。不过，对于本文方法，子空间是可选的，η=0时，即能保证不丢失信息（可能含噪声），分类精度亦能与其他算法匹敌。而就模糊系统而言，需要强调的是，当采用特征子空间时，结合网格划分法，本文方法的规则语义更简洁，可解释性更好。

一般而言，模糊规则数K会小于训练样本数N，于是本文方法的时间复杂度为O(KNt+K2N)，其中t为FSC算法的迭代次数，KM算法最坏时间复杂度和岭回归的时间复杂度都是O(K2N)。KRR的时间复杂度和SVM最坏时间复杂度为O(N3)。训练过程中，本文方法分为3段，包含多个超参数，FSC需要迭代，KM算法涉及排序过程，因而实际用时相比部分算法不具有优势。

5 结束语

针对传统的区间二型TSK模糊系统存在的不足，本文使用模糊子空间聚类和网格划分相结合的方法生成稀疏的规整的规则中心，并简化规则后件为0阶形式，从而得到规则语义更为简洁，可解释性更好的区间二型模糊子空间0阶TSK系统。对于特征子空间较为明显的数据，本文方法可发挥去噪、易于解释等优势；对于特征子空间不够明显的数据，本文方法可取η=0，使用完整的特征空间，保证不丢失信息的完整性。未来工作中，需要研究如何自动识别数据有无特征子空间，以使算法更加智能化。

Table 4 Classification accuracies of different methods on real datasets表4 真实数据集上各算法的分类精度

[1]Güner H AA,Yumuk H A.Application of a fuzzy inference system for the prediction of longshore sediment transport[J].Applied Ocean Research,2014,48(48):162-175.

[2]Takagi T,Sugeno M.Fuzzy identification of systems and its applications to modeling and control[J].IEEE Transactions on Systems,Man,and Cybernetics,1985,15(1):116-132.

[3]Jang J S R.ANFIS:Adaptive-network-based fuzzy inference systems[J].IEEE Transactions on Systems,Man,and Cybernetics,1993,23(3):665-685.

[4]Castillo O,Melin P.Type-2 fuzzy logic:theory and applications[M]//Studies in Fuzziness and Soft Computing.Berlin,Heidelberg:Springer,2007.

[5]Juang C F,Tsao Y W.A self-evolving interval type-2 fuzzy neural network with online structure and parameter learning[J].IEEE Transactions on Fuzzy Systems,2008,16(6):1411-1424.

[6]Juang C F,Huang Renbo,Cheng Weiyuan.An interval type-2 fuzzy-neural network with support-vector regression for noisy regression problems[J].IEEE Transactions on Fuzzy Systems,2010,18(4):686-699.

[7]Deng Zhaohong,Choi K S,Cao Longbing,et al.T2FELA:type-2 fuzzy extreme learning algorithm for fast training of interval type-2 TSK fuzzy logic system[J].IEEE Transactions on Neural Networks&Learning Systems,2014,25(4):664-676.

[8]Rubio-Solis A,Panoutsos G.Interval type-2 radial basis function neural network:a modeling framework[J].IEEE Transactions on Fuzzy Systems,2015,23(2):457-473.

[9]Karnik N N,Mendel J M.Centroid of a type-2 fuzzy set[J].Information Sciences,2001,132(1/4):195-220.

[10]Mendel J M.Computing derivatives in interval type-2 fuzzylogic systems[J].IEEE Transactions on Fuzzy Systems,2004,12(1):84-98.

[11]Wu Dongrui,Mendel J M.Enhanced Karnik-Mendel algorithms[J].IEEE Transactions on Fuzzy Systems,2009,17(4):923-934.

[12]Kisi O,Zounemat-Kermani M.Comparison of two different adaptive neuro-fuzzy inference systems in modelling daily reference evapotranspiration[J].Water Resources Management,2014,28(9):2655-2675.

[13]Wong S Y,Yap K S,Yap H J,et al.On equivalence of FIS and ELM for interpretable rule-based knowledge representation[J].IEEE Transactions on Neural Networks&Learning Systems,2015,26(7):1417-1430.

[14]Deng Zhaohong,Zhang Jiangbin,Jiang Yizhang,et al.Fuzzy subspace clustering based 0-order ridge regression TSK fuzzy system[J].Control and Decision,2016,31(5):882-888.

[15]Gan Guojun,Wu Jianhong,Yang Zijiang.A fuzzy subspace algorithm for clustering high dimensional Data[C]//LNCS 4093:Proceedings of the 2nd International Conference on Advanced Data Mining and Applications,Xi'an,China,Aug 14-16,2006.Berlin,Heidelberg:Springer,2006:271-278.

[16]Gan G,Wu J.A convergence theorem for the fuzzy subspace clustering(FSC)algorithm[J].Pattern Recognition,2008,41(6):1939-1947.

[17]Hoerl A E,Kennard R W.Ridge regression:biased estimation for nonorthogonal problems[J].Technometrics,1970,12(1):55-67.

[18]Hartigan J A,Wong M A.Algorithm AS 136:ak-means clustering algorithm[J].Journal of the Royal Statistical Society:Series CApplied Statistics,1979,28(1):100-108.

[19]Bezdek J C,Ehrlich R,Full W.FCM:The fuzzy C-means clustering algorithm[J].Computers&Geosciences,1984,10(84):191-203.

[20]Priyono A,Ridwan M,Alias A J,et al.Generation of fuzzy rules with subtractive clustering[J].Jurnal Teknologi,2012,43(1):143-153.

[21]An Senjian,Liu Wanquan,Venkatesh S.Fast cross-validation algorithms for least squares support vector machine and kernel ridge regression[J].Pattern Recognition,2007,40(8):2154-2162.

[22]Shawe-Taylor J,Cristianini N.An introduction to support vector machines and other kernel-based learning methods[M].New York:Cambridge University Press,2000:93-112.

[23]Huang Guangbin,Zhu Qinyu,Siew C K.Extreme learning machine:theory and applications[J].Neurocomputing,2006,70(1/3):489-501.

[24]Huang Guangbin,Zhou Hongming,Ding Xiaojian,et al.Extreme learning machine for regression and multiclass classification[J].IEEE Transactions on Systems,Man,and Cybernetics:Part B Cybernetics,2012,42(2):513-529.

[25]Chang C C,Lin C J.LIBSVM:a library for support vector machines[J].ACM Transactions on Intelligent Systems and Technology,2011,2(3):27.

附中文参考文献：

[14]邓赵红,张江滨,蒋亦樟,等.基于模糊子空间聚类的0阶岭回归TSK模糊系统[J].控制与决策,2016,31(5):882-888.

Interval Type-2 Fuzzy Subspace Zero-Order TSK System*

CHEN Junyong+,DENG Zhaohong,WANG Shitong
School of Digital Media,Jiangnan University,Wuxi,Jiangsu 214122,China

A

TP181

+Corresponding author:E-mail:enjolras1024@163.com

CHEN Junyong,DENG Zhaohong,WANG Shitong.Interval type-2 fuzzy subspace zero-order TSK system.Journal of Frontiers of Computer Science and Technology,2017,11(10)：1652-1661.

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2017/11(10)-1652-10

10.3778/j.issn.1673-9418.1608023

E-mail:fcst@vip.163.com

http://www.ceaj.org

Tel:+86-10-89056056

*The National Natural Science Foundation of China under Grant No.61170122(国家自然科学基金);the Outstanding Youth Fund of Jiangsu Province under Grant No.BK20140001(江苏省杰出青年基金).

Received 2016-08,Accepted 2016-10.

CNKI网络优先出版:2016-10-18,http://www.cnki.net/kcms/detail/11.5602.TP.20161018.1622.014.html

CHEN Junyong was born in 1990.He is an M.S.candidate at Jiangnan University.His research interests include artificial intelligence and neural fuzzy computation.

陈俊勇（1990—），男，安徽池州人，江南大学硕士研究生，主要研究领域为人工智能，神经模糊计算。

DENG Zhaohong was born in 1981.He received the Ph.D.degree in light industry information technology and engineering from Jiangnan University in 2008.Now he is a professor and M.S.supervisor at Jiangnan University.His research interests include artificial intelligence and neural fuzzy computation.

邓赵红（1981—），男，安徽蒙城人，2008年于江南大学轻工信息与技术专业获得博士学位，现为江南大学教授、硕士生导师，主要研究领域为人工智能，神经模糊计算。

WANG Shitong was born in 1964.He received the M.S.degree in computer science from Nanjing University of Aeronautics and Astronautics in 1987.Now he is a professor and Ph.D.supervisor at Jiangnan University.His research interests include artificial intelligence and pattern recognition.

王士同（1964—），男，江苏扬州人，1987年于南京航空航天大学获得硕士学位，现为江南大学教授、博士生导师，主要研究领域为人工智能，模式识别。