面向基因数据分类的核主成分分析旋转森林算法*
2017-10-12陆慧娟刘亚卿孟亚琼刘砚秋
陆慧娟,刘亚卿,孟亚琼,关 伟,刘砚秋
1.中国计量大学 信息工程学院,杭州 310018
2.中国计量大学 现代科技学院,杭州 310018
面向基因数据分类的核主成分分析旋转森林算法*
陆慧娟1+,刘亚卿1,孟亚琼1,关 伟2,刘砚秋1
1.中国计量大学 信息工程学院,杭州 310018
2.中国计量大学 现代科技学院,杭州 310018
Abstract:Rotation forest(RoF)algorithm is an ensemble classification algorithm using linear analysis theory and decision trees.The rotation forest achieves higher classification accuracy and superior performance with less number of classifiers.However,the classification accuracy decreases for gene expression data with linearly inseparable cases.To address this issue,this paper proposes a rotation forest algorithm based on kernel principal component analysis(KPCA-RoF),chooses the Gaussian kernel function and principal component analysis to implement the nonlinear mapping and deal with differences in gene data.The proposed algorithm focuses on the optimization of parameters,and uses decision tree algorithm for ensemble learning.Experiments show that the new algorithm well addresses the linearly inseparabal issue and improves the classification accuracy.
Key words:kernel function;principal component analysis;decision tree;rotation forest;gene data classification
旋转森林(rotation forest,RoF)是一种运用线性分析理论和决策树的集成分类算法,在分类器个数较少的情况下仍可以取得良好的结果,同时能保证集成分类的准确性。但对于部分基因数据集,存在线性不可分的情况,原始的算法分类效果不佳。提出了一种运用核主成分分析变换的旋转森林算法(rotation forest algorithm based on kernel principal component analysis,KPCA-RoF),选择高斯径向基核函数和主成分分析的方法对基因数据集进行非线性映射和差异性变化,着重于参数的选择问题,再利用决策树算法进行集成学习。实验证明,改进后的算法能很好地解决数据线性不可分的情形,同时也提高了基因数据集上的分类精度。
核函数;主成分分析;决策树;旋转森林;基因数据分类
1 引言
癌症是严重威胁人类健康的一大疾病,已经成为我国主要的公共卫生问题之一。目前癌症的发病率和死亡率一直呈上升趋势,因此预防和治疗癌症是全世界关注的焦点问题[1]。然而,人类肌体从癌变的发生,到有明显症状的出现,要经过一个较长的潜伏期,如果在此期间能够及时发现,并且进行有效的干预,就可以将肿瘤控制或扼杀在萌芽状态。依靠基因表达数据进行肿瘤诊断分类是目前比较热门的一种分类方法,对于基因数据的分类问题,目前主要集中在分类精度、泛化能力、算法的复杂性和可理解性上。但是由于基因表达数据维数高、小样本和非线性等特点,使得基因表达数据的分析遇到一定的困难。且对于部分基因数据集,存在线性不可分的情况,原始的旋转森林(rotation forest,RoF)算法在对线性不可分的基因数据集进行分类时容易出现分类精度低,耗时长等问题。对样本数据的筛选、特征选择、降维、数据分类等都是当前数据挖掘和机器学习中的研究热点,清楚差异基因的功能和对其进行干预而引起的结果,并最终可以根据获得的信息进行诊断和治疗[2]。
旋转森林[3]是于2006年提出的一种分类器集成系统,其基本思想建立在随机森林算法基础上。旋转森林把原特征空间分割成若干子集,之后对每个子集分别进行某种线性变换。如主成分分析(principal components analysis,PCA),保留所有主成分的情况下,将得到的变换分量分别按照这些子集原来对应的顺序合并,这样每次随机分割后得到的数据集都被投影到不同坐标空间中,从而形成差别较大的分量子集,用这些分量自己训练分类器,能够得到差异较大且分类性能较高的基分类器,以提高集成分类的性能。
毛莎莎等人[4]利用旋转森林集成方式,集成了两种不同的模型,充分利用两种模型各自的优势,为形成异构算法集成提供了启示。Mousavi等人[5]结合了旋转森林和集成剪枝两种方法,并提出了EP-RTF(ensemble pruning and rotation forest)算法。首先通过遗传算法选择异构的分类器子集,其次运用旋转森林方法进行训练,参数由遗传算法进行优化,并使用加权投票的方式得出最终结果。Wong等人[6]将旋转森林分类器和LPQ(local phase quantization)算法相结合,验证了旋转森林和支持向量机分类器的良好性能,同时也为未来的蛋白质研究提供了理论基础。不过从目前的文献来看,对旋转森林算法的研究和应用依然不多,有很多地方值得进一步深入探讨。
本文提出了一种运用核主成分分析变换的旋转森林算法(rotation forest algorithm based on kernerl principal component analysis,KPCA-RoF)。利用核主成分分析的方法进行数据的非线性映射和差异性变换,并选择合适的参数,利用决策树算法进行集成学习,形成核函数旋转森林算法。实验表明,核旋转森林方法在同等集成度的条件下具有更高的分类精度,这在一定程度上可以解决基因数据线性不可分的情形。
2 核函数相关理论
对于任意一数据集T有以下关系:
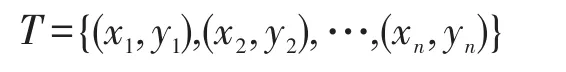
其中,i=1,2,…,n,Rn表示n维空间。如果存在一个超平面S:

可以将两类样本完全分开,则称数据集T为线性可分数据集。
一个数据集是否线性可分,取决于是否能找到一个超平面来分离两个相邻的类别。如果每个类别的分布范围本身是全连通的单一凸集,且没有重叠部分,则这两个类别就是线性可分的。如果存在的多种模式可以用n维欧式空间的点分开,则可以在此空间中形成一个曲面把归属于不同模式的样本点完全隔开,如支持向量机(support vector machine,SVM)[7]就可以很好地分类。线性不可分的现象,简单来说就是一个数据集不可以通过一个线性分类器(直线、平面)来实现正确的分类。如图1所示。
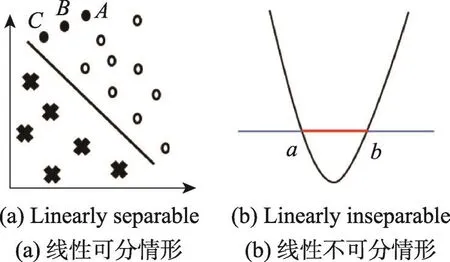
Fig.1 Linearly separable and linearly inseparable图1 线性可分与线性不可分
对于线性不可分的情形,可以采用核函数映射的方式得到其特征空间,之后在此基础上进一步操作。但是采用直接映射的方法在高维空间进行操作是不可行的,因为直接映射本身就存在着计算复杂等技术问题,且映射函数的形式和参数也不容易把握,借助核函数的方法可以间接地实现此种映射[8]。
以下列举几种常用的核函数:
(1)线性核函数
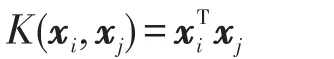
(2)P阶多项式核函数
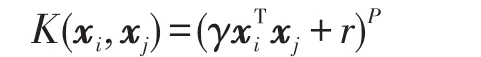
(3)高斯径向基核函数(radialbasisfunction,RBF)
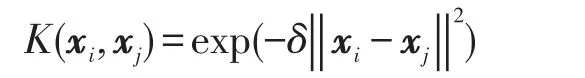
将样本集作为输入,高维的特征空间作为输入空间,许多的传统线性分类算法就可以实现非线性分类,这是基于核的机器学习算法应用的基础。虽然其中的映射函数非常复杂甚至难以求出,但是可以通过核函数绕过此问题,使此方法变得容易应用。高斯径向基核函数由于更小的数值复杂度和较少的参数,以及较强的代表性而成为核函数的首选方法[9],通过调整核函数参数的大小控制其过拟合的程度而得到合适的算法。
3 核主成分分析
假设x1,x2,…,xm为训练样本,xk∈RN用来表示其输入空间。选定映射函数为Φ,其定义如下:
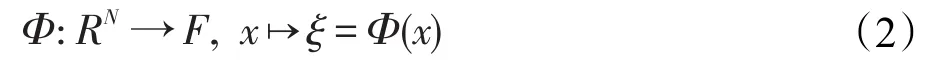
核函数通过映射关系Φ先实现输入样本点x到特征空间F的映射,F由Φ(x1),Φ(x2),…,Φ(xm)生成,中心化处理映射后的数据,即:

则映射后特征空间的协方差矩阵为:

按照主成分分析的方式求解特征方程:

λ和V是属于Φ(xi)的生成空间中的特征值和特征向量,因此:
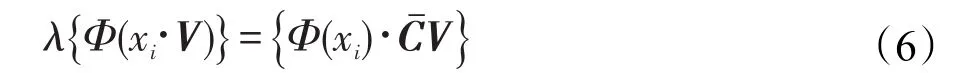
并且存在参数αi,使得V可由Φ(xi)线性表示,即:

合并式(6)、(7),把映射后数据的相互内积定义成一个m阶的矩阵K,其元素根据选择的核函数计算所得:

则可以得到与式(5)等价的公式:

其中,α=(α1,α2,…,αm)T,矩阵K就是以后所要用到的变换矩阵[10]。
求解K的特征值和特征向量。设K的特征值为λ1≤λ2≤ …≤λm,所对应的特征向量为α1,α2,…,αm。
4 算法描述
4.1 基于核主成分分析的旋转森林算法
核函数方法可以按照模块化的形式扩展机器学习算法,基于这一原理,选择利用核主成分分析的方式实现样本数据的变换,并形成差异性强的训练集,之后再参照旋转森林算法以决策树为基分类器,形成核主成分分析旋转森林算法。算法描述如图2所示。
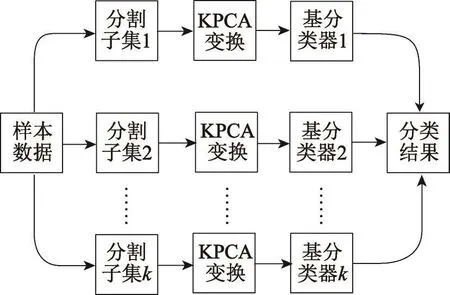
Fig.2 Description of KPCA-RoF图2 核主成分分析旋转森林算法描述
(1)对一给定的n维样本集,取除去类标的特征集部分为H,划分为不相交的K份。
(2)设D1,D2,…,DL为要用于分类的基分类器。Hij表示Di分类器所使用训练集中对应的第j个特征子集,其中1≤i≤L,1≤j≤K。对样本集进行随机抽样m次,抽样形成样本子集Zi,并且m=n/k,Zij表示Hij所对应的样本子集。对Zij选择某核函数进行核主成分分析,排列其特征向量产生一个新的系数矩阵Cij。
(3)重复上述步骤,对每个Zi通过核主成分分析的方式产生一个系数矩阵,共重复了K次。
(4)将上述产生的系数矩阵组合成一个巨大的稀疏矩阵,以此生成基分类器Di的旋转矩阵Ri:
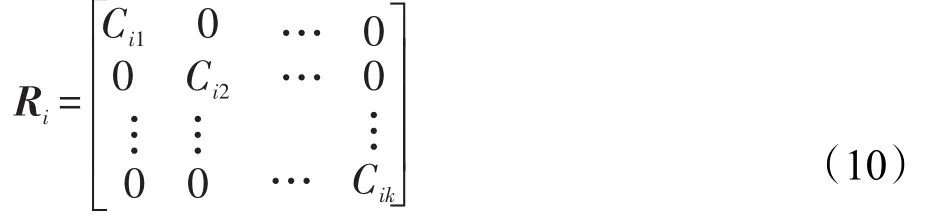
这样分类器Di所使用的训练集则为ZRi。同样在测试过程中,对于新样本x,也要与旋转矩阵相乘得到xRi再送入分类器,判定其类别的置信度为:

4.2 核函数的选择方法以及参数的选择方法
因为不同的核函数会对分类效果带来较大的差异,不适当的函数形式或者参数甚至有可能达不到分类的效果。单独对核函数进行评价,通过测算映射后数据的类内聚集和类间离散程度来评估可分性的好坏[11]。这种方法独立于具体的分类算法,也不考虑最后的泛化能力,因而适用性较强。本文采用高斯核函数改进旋转森林算法,并关注于参数的选择问题。
这里对参数的优化选用特征类间距作为参考指标[12]。数据映射后在特征空间中的夹角和距离为:
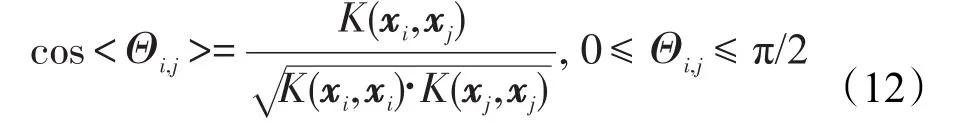
用Di,j来表示两个向量之间的距离,表示如下:
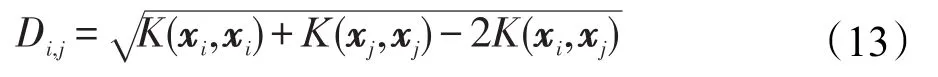
将具体的核函数代入式(12)和(13):
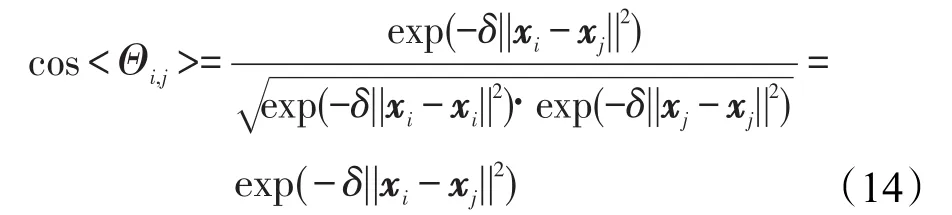
其中夹角满足:

同理可得出:
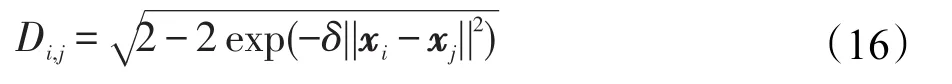
从上述表达式可得,仅有一个参数影响类间距和夹角,从而影响特征空间的分布情况,进一步影响旋转森林算法的分类效果。
当参数δ的值趋于0时,可以得出其夹角的余弦值趋于1,也即意味着映射后的两向量夹角值趋于0;并且通过计算向量距离可知,向量的距离也趋于0,这意味着所有的样本被映射到一点上了,这样根本无法对样本进行分类。当参数δ的值趋于无穷大时,两向量夹角趋于π/2,样本的距离趋于一个常数,这说明样本集被映射到一个n维的特征空间中,且可以发现特征向量是两两正交。因此特征空间的维数随着δ的增大而单调增大,一直增加到n(n是样本空间样本的个数);并且特征空间各向量之间的夹角以及距离也是单调增加的,分别趋于π/2和。
给定一个包含有L个样本C个类别的训练集X,即:

计算样本映射后在特征空间中的平均值:
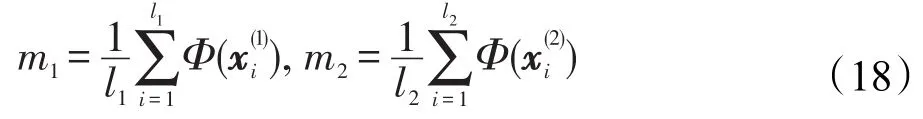
则在映射后的空间中类间平均距离的表达式为:
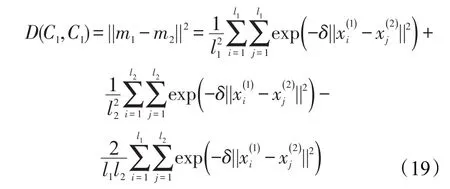
在核空间中类间余弦值为:
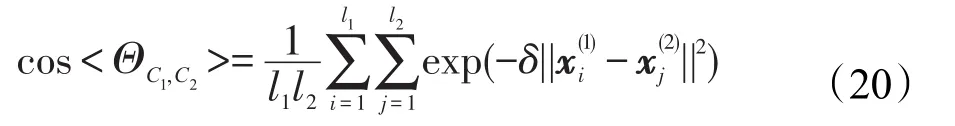
在核空间中类内余弦值为:
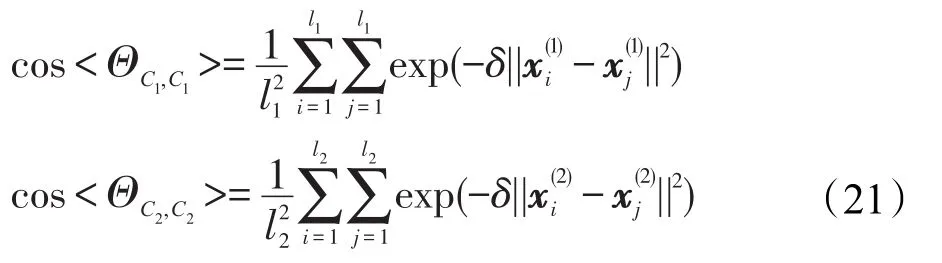
综合式(19)、(20)、(21)可得:
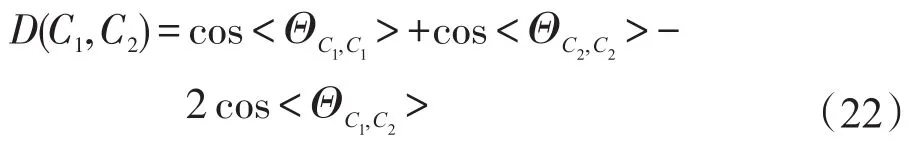
通过上述表达式可知,类间距可以表述为类间角和类内角的运算结果。当类内角大,类间角小时,类间距较大;反之则类间距较小。而根据式(14)可知,类间角和类内角均随着δ的增大而增大,因此可能存在一个参数值,使得类间距最大。
5 实验结果及分析
本实验主要选择高斯径向基核函数对样本进行变换,对比指标主要有分类精度、集成度等。通过对核函数唯一的参数δ进行优化[13],使之获得较好的分类性能。
本实验选定Breast(乳腺癌)、CNS(神经系统肿瘤组织)、ALL(急性淋巴细胞白血病)3个数据集作为实验对象,数据来源均可以从公开的站点下载,其下载网址为http://datam.i2r.a-star.edu.sg/datasets/krbd/。因为原始数据集的维数过高,不利于直接进行数据分类,所以先利用ReliefF算法[14]进行一定程度上的降维处理。ReliefF算法是一种带有特征权重的选择方法,这里对数据集随机抽样30次,特征阈值设为0.95,得出预处理后的数据集。按照上述方法通过实验的手段取得各数据集的最佳参数。下面是有关的曲线δ-J(δ),δ的取值范围为δ={10-5,10-4,…,105}。
图3表示3组数据各自的参数值与其归一化的类间距之间的关系,均采用30次实验的平均值。可以看出,在可观测到的范围内[10-6,106],存在着极大值点,分别是0.9、0.9、0.8。则认为对于这3组数据集,最优的参数值分别为δ1=δ2=0.9,δ3=0.8。
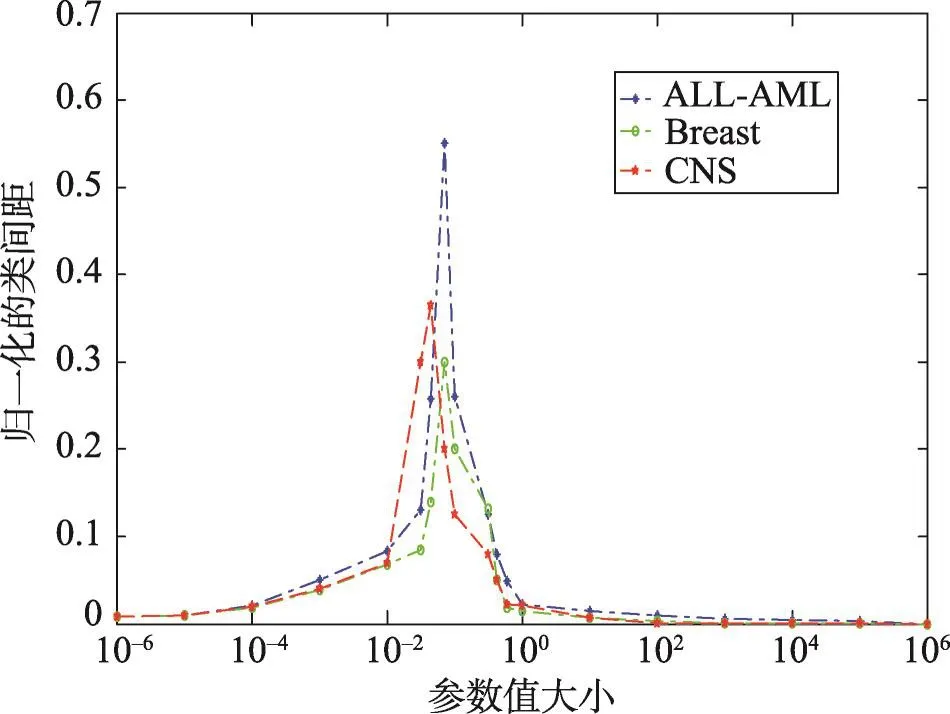
Fig.3 Parameter values and class separation distance图3 参数值与类间距的关系
本文主要通过与Bagging算法[15]、随机森林算法以及原始的旋转森林算法进行比较实验和分析,依次验证改进后的旋转森林算法的有效性。所有算法的基分类器都采用C4.5决策树[16],主要控制的变量有集成度N和抽取的样本个数M,每次均做到控制单一量的变化,分别取最好的结果进行对比实验。实验统计量为F检验,样本方差为S2,样本均值为Xˉ。
(1)高斯径向基核旋转森林(RBF-RoF)特征集分割数实验。
表1在基于决策树的集成数为30的情况下,不断地改变各特征集的分割数后所得到的分类精度。保证基分类器的数目足够多,这样就可以使得每个实验数据集充分集成。从实验结果得到,在特征集分割数大于10时,分割数的改变对于提高旋转森林的分类精度不会带来很大的改善,这跟原始的旋转森林实验的结果类似。因此在后续的实验中,没必要再去增加特征集的分割数,保持在5~10之间的任何一个值即可,这里选择N=9。

Table 1 Classification accuracy and the number of feature set splitting表1 分类精度与特征集分割数之间的关系
表2展示了随着集成度的上升,各数据集分类精度的变化。从结果可以得到,随着集成度的上升,各数据集大约在集成度为15时获得较好的精度,之后就几乎稳定下来。分别在每一个数据集上选用几种集成算法,实验变量为集成度,验证不同集成算法所带来的分类效果。

Table 2 Classification accuracy and integration level表2 分类精度与集成度之间的关系
图4~图6分别展示了各数据集在不同分类算法下的分类精度,对比结果可以发现,随着集成度的上升,各分类算法的精度都会有所上升。总体来讲,Bagging决策树的分类精度最差,随机森林稍好,旋转森林更好一些,经过高斯径向基核函数改进的核主成分分析旋转森林(RBF-RoF)效果总是最好的。Bagging决策树仅仅是对决策树的集成,不会对算法性能带来明显的提升,随机森林增加了对特征空间的随机分割,基分类器间存在一定的差异性。从上述实验结果可以看出,旋转森林和RBF-RoF都会取得良好的实验效果,这是由于这两种算法对特征空间进行分割和变换。对比改进前后的旋转森林,改进后的分类精度会有所提升;同时,改进后的旋转森林在比较小的集成度时就可以取得很好的精度,这说明进行非线性变换相比线性变换会带来更好的可分性,同时非线性变换会增加很多的计算量,但算法的复杂度同属于O(n3),复杂度影响并不明显,相对于精度的提高,可以忽略。
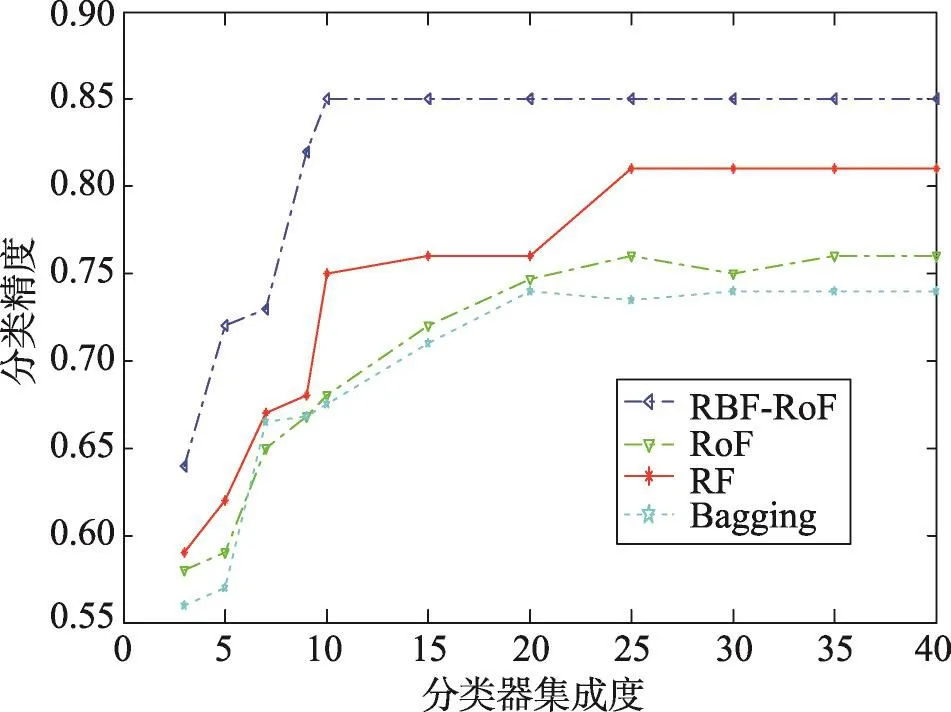
Fig.4 Classification accuracy of Breast dataset图4 Breast数据集的分类精度
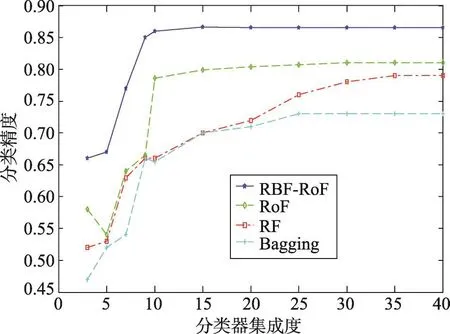
Fig.5 Classification accuracy of CNS dataset图5 CNS数据集的分类精度
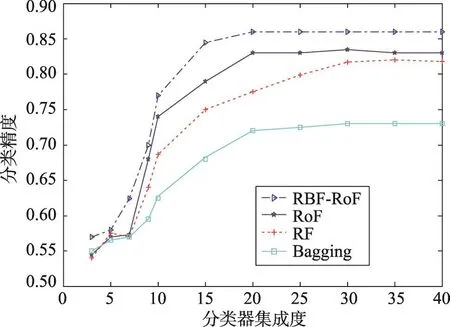
Fig.6 Classification accuracy ofALL dataset图6 ALL数据集的分类精度
(2)通过对改进后的算法进行统计学分析,以说明比原始算法存在显著性差别。这里利用F检验的方法来验证改进前后的显著性。
求解实验结果样本的方差S2:

进一步求得F值:

其中一般取参数α=0.05,与F分布表中所查到的值进行比对,如果前者大于后者,则认为本组算法之间是彼此显著的,否则就认为差别不大。
表3列举了几个常用的统计量,样本均值、方差S2以及显著性F。从计算结果可以得到,在各个数据集上表现显著性有效。

Table 3 Statistics analysis of algorithms表3 算法改进前后的统计量分析
6 结束语
通过特征集分割、采样与变换,最后再重新生成一个变换矩阵,是旋转森林的重要特点。借助核支持向量机的思想以及旋转森林算法的流程,实现了基于高斯径向基核主成分分析的旋转森林,与利用线性变换的旋转森林算法相比,分类精度得到提高。并通过对其他统计量的分析可知,改进后的算法方差更小,并且比原始算法更显著。尽管改进后的算法会带来更多的资源消耗,例如计算时间和内存,但是在计算成本越来越低的现今社会,这不应该成为一种瓶颈。
[1]Lu Huijuan.A study of tumor classification algorithms using gene expression data[D].Xuzhou:China University of Mining and Technology,2012.
[2]Lu Huijuan,An Chunlin,Zheng Enhui,et al.Dissimilarity based ensemble of extreme learning machine for gene expression data classification[J].Neurocomputing,2014,128(5):22-30.
[3]Liu Min,Xie Huosheng.Ensemble co-training algorithm based on rotation forest[J].Computer Engineering and Applications,2011,47(30):172-175.
[4]Mao Shasha,Xiong Lin,Jiao Licheng,et al.Isomerous multiple classifier ensemble via transformation of the rotation forest[J].Journal of Xidian University,2014,41(5):48-53.
[5]Mousavi R,Eftekhari M,Haghighi M G.A new approach to human microRNA target prediction using ensemble pruning and rotation forest[J].Journal of Bioinformatics and Computational Biology,2015,13(6):1550017.
[6]Wong Leon,You Zhuhong,Ming Zhong,et al.Detection of interactions between proteins through rotation forest and local phase quantization descriptors[J].International Journal of Molecular Sciences,2015,17(1):21.
[7]Adankon M M,Cheriet M.Support vector machine[M]//Encyclopedia of Biometrics.[S.l.]:Springer US,2015:1303-1308.
[8]Lu Huijuan,Du Bangjun,Liu Jinyong,et al.A kernel extreme learning machine algorithm based on improved particle swam optimization[J].Memetic Computing,2017,9(2):121-128.
[9]Jian Ling.Kernel based learning algorithm and application[D].Dalian:Dalian University of Technology,2012.
[10]Li Zhe,Kruger U,Xie Lei,et al.Adaptive KPCA modeling of nonlinear systems[J].IEEE Transactions on Signal Processing,2015,63(9):2364-2376.
[11]Song Xiaoshan,Jiang Xiaoyu,Luo Jianhua,et al.Analysis of the inter-class distance-based kernel parameter evaluating method for RBF-SVM[J].Acta Armamentarii,2012,33(2):203-208.
[12]Wang Tinghua,Chen Junting.Survey of research on kernel function evaluation[J].Application Research of Computers,2011,28(1):25-28.
[13]Qiu Xiaoyu.The selection for the kernel-based method[D].Jinan:Shandong Normal University,2008.
[14]Chen Xiaolin,Ji Bo,Ye Yangdong.A R-NIC algorithm based on ReliefF feature weighting[J].Computer Engineering,2015,41(4):161-165.
[15]Li Yaqin,Yang Huizhong.Ensemble modeling method based on Bagging algorithm and Gaussian process[J].Journal of Southeast University:Natural Science Edition,2011,41(S1):93-96.
[16]Meng Yang,Hou Feifei.Node association mining based on C4.5[J].Telecom World,2016(10):131-132.
附中文参考文献:
[1]陆慧娟.基于基因表达数据的肿瘤分类算法研究[D].徐州:中国矿业大学,2012.
[3]刘敏,谢伙生.一种基于旋转森林的集成协同训练算法[J].计算机工程与应用,2011,47(30):172-175.
[4]毛莎莎,熊霖,焦李成,等.利用旋转森林变换的异构多分类器集成算法[J].西安电子科技大学学报:自然科学版,2014,41(5):48-53.
[9]渐令.基于核的学习算法与应用[D].大连:大连理工大学,2012.
[11]宋小衫,蒋晓瑜,罗建华,等.基于类间距的径向基函数——支持向量机核参数评价方法分析[J].兵工学报,2012,33(2):203-208.
[12]汪廷华,陈峻婷.核函数的度量研究进展[J].计算机应用研究,2011,28(1):25-28.
[13]邱潇钰.核函数的参数选择[D].济南:山东师范大学,2008.
[14]陈晓琳,姬波,叶阳东.一种基于ReliefF特征加权的RNIC算法[J].计算机工程,2015,41(4):161-165.
[15]李雅芹,杨慧中.一种基于Bagging算法的高斯过程集成建模方法[J].东南大学学报,2011,41(S1):93-96.
[16]孟杨,候飞飞.基于C4.5的节点关联挖掘[J].通讯世界,2016(10):131-132.
Classifier Algorithm of Genetic Data Based on Kernel Principal Component Analysis and Rotation Forest*
LU Huijuan1+,LIU Yaqing1,MENG Yaqiong1,GUAN Wei2,LIU Yanqiu1
1.College of Information Engineering,China Jiliang University,Hangzhou 310018,China
2.College of Modern Science and Technology,China Jiliang University,Hangzhou 310018,China





A
TP181
+Corresponding author:E-mail:hjlu@cjlu.edu.cn
LU Huijuan,LIU Yaqing,MENG Yaqiong,et al.Classifier algorithm of genetic data based on kernel principal component analysis and rotation forest.Journal of Frontiers of Computer Science and Technology,2017,11(10):1570-1578.
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology
1673-9418/2017/11(10)-1570-09
10.3778/j.issn.1673-9418.1608046
E-mail:fcst@vip.163.com
http://www.ceaj.org
Tel:+86-10-89056056
*The National Natural Science Foundation of China under Grant Nos.61272315,60905034(国家自然科学基金);the Natural Science Foundation of Zhejiang Province under Grant No.Y1110342(浙江省自然科学基金);the National Security Bureau Project under Grant No.zhejiang-00062014AQ(国家安全总局项目).
Received 2016-08,Accepted 2016-10.
CNKI网络优先出版:2016-10-19,http://www.cnki.net/kcms/detail/11.5602.TP.20161019.1458.008.html
LU Huijuan was born in 1962.She received the Ph.D.degree from China University of Mining and Technology in 2012.Now she is a professor at China Jiliang University,and the outstanding member of CCF.Her research interests include machine learning,pattern recognition and bioinformatics,etc.She has published over 80 papers,conducted 2 National Natural Science Foundation of China projects and 8 Science&Technology projects of Zhejiang Province.
陆慧娟(1962—),女,浙江东阳人,2012年于中国矿业大学获得博士学位,现为中国计量大学教授,CCF杰出会员、理事,主要研究领域为机器学习,模式识别,生物信息学等。发表学术论文80多篇,主持完成国家自然科学基金项目2项,浙江省级科技项目8项。
LIU Yaqing was born in 1988.His research interests include machine learning,cloud computing and data mining,etc.
刘亚卿(1988—),男,河南周口人,硕士,主要研究领域为机器学习,云计算,数据挖掘等。
MENG Yaqiong was born in 1992.She is an M.S.candidate at China Jiliang University,and the member of CCF.Her research interests include machine learning and data mining,etc.
孟亚琼(1992—),女,安徽芜湖人,中国计量大学硕士研究生,CCF会员,主要研究领域为机器学习,数据挖掘等。
GUAN Wei was born in 1976.He is a lecturer at China Jiliang University,and the member of CCF.His research interests include machine learning and pattern recognition,etc.
关伟(1976—),男,湖北仙桃人,硕士,中国计量大学讲师,CCF会员,主要研究领域为机器学习,模式识别等。
LIU Yanqiu was born in 1977.She is an associate professor at China Jiliang University,and the member of CCF.Her research interests include machine learning,data mining and image processing,etc.
刘砚秋(1977—),女,河南洛阳人,硕士,中国计量大学副教授,CCF会员,主要研究领域为机器学习,数据挖掘,图像处理等。
