(1≤α<2)在Chebyshev结点组的有理逼近

2017-10-11程一元张永全费经泰

中国计量大学学报 2017年3期

关键词：有理安庆结点

程一元，张永全,费经泰

(1.中国计量大学理学院，浙江杭州 310018；2. 安庆师范大学数学与计算科学学院，安徽安庆 246133)

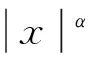
程一元1，张永全1,费经泰2

(1.中国计量大学理学院，浙江杭州 310018；2. 安庆师范大学数学与计算科学学院，安徽安庆 246133)

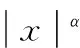
有理逼近; Chebyshev结点; Newman-α型有理算子

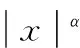
Keywords: rational approximation; Chebyshev nodes; Newman-αtype rational operator

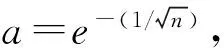
1 相关定义及引理

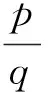
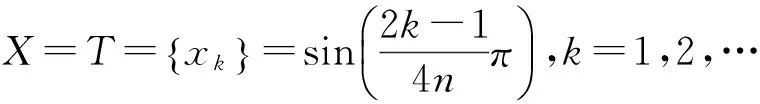
类似于Newman型有理算子定义如下:Newman-α型有理算子

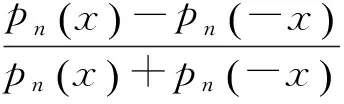
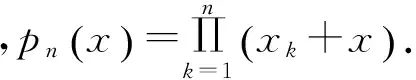
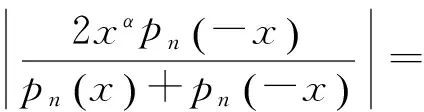
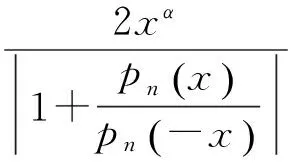
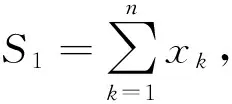
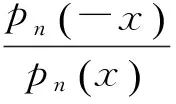
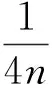
证明:根据计算可得

则有

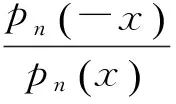
又因为|>Tn(x)|≤1,∀x∈[-1,1].所以当x≥x1时,有

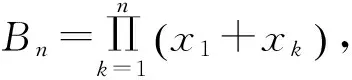
由文献[12]中

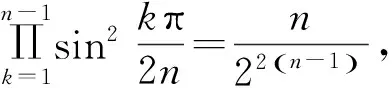
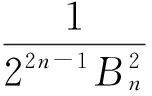
2 主要结果

定理1:结点组X取

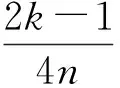
对于∀x∈[-1,1],当n充分大时

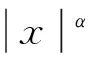
nΛ2n-1(T).

其中Λ2n-1(T)是Lebesgue常数,由文献[2]中可知:

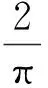
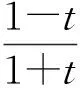
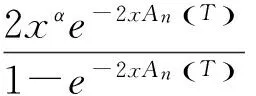
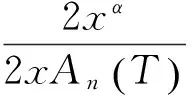
其中Cα是含α的常量.

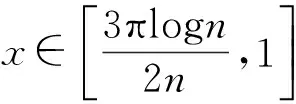
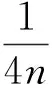
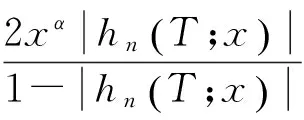
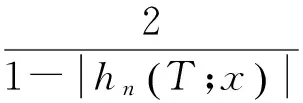
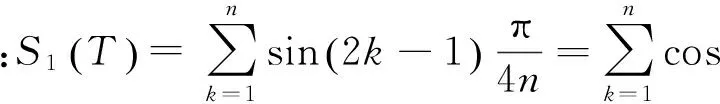
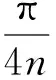
由引理1可知,

故可以得到

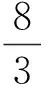
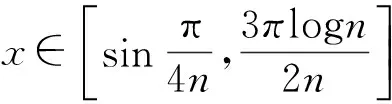
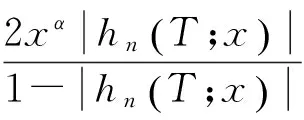
其中Dα是含α的常量.

所以综合三种情形有

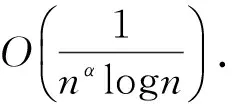
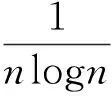
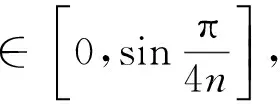
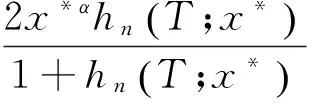
下证当n充分大时,hn(T;x*)是有界量.令

可以得到

又因为

从而

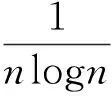
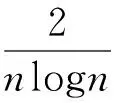
2nπ+o(1)

(n→∞),

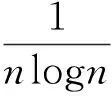
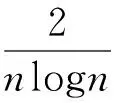
(n→∞).

所以有

最后我们得到：

然后令

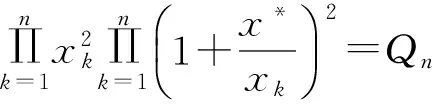
同时有

利用log(1+x)≤x(x≥0)可得到logRn=

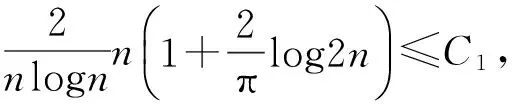
所以当n充分大时,

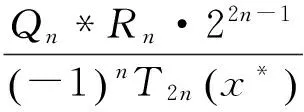
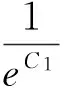
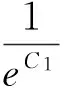
定理2得证.

由以上定理1,定理2可得

3 结语

[1] NEWMAN D J. Rational approximation to |x| [J].MichiganMathematicalJournal, 1964,11(1) : 11-14.

[2] BRUTMAN L, PASSOW E. Rational interpolation to |x| at the Chebyshev nodes [J].BulletinoftheAustralianMathematicalSociety,1997,56(1) :81-86.

[3] 张慧明,李建俊. |x|在第二类Chebyshev结点的有理逼近[J].郑州大学学报(理学版),2010,42(2) :1-3. ZHANG H M,LI J J. Rational approximation to |x| at the Chebyshev nodes of the second kind[J].JournalofZhengzhouUniversity(NaturalScienceEdition), 2010,42(2) :1-3

[4] BRUTMAN L. On rational interpolation to |x| at the adjusted Chebyshev nodes[J].JournalofApproximationTheory, 1998,95(1) :146-152.

[5] ZHAO Y, ZHOU S P. Some remarks on rational interpolation to |x| [J].JournalofMathematicalResearch&Exposition,2003, 23(1) :65-70.

[6] 高淇琦, 谢庭藩. 一类神经网络对连续函数的逼近[J]. 中国计量学院学报, 2011, 22(1) :84-91. GAO Q Q, XIE T F. Approximation of continuous functions by a class of neural network[J].JournalofChinaUniversityofMetrology, 2011, 22(1) :84-91.

[7] 戴慧丽. 两类Chebyshev零点的Newman型有理算子逼近|x|的渐近性质[J]. 中国计量学院学报, 2006, 17(3) :243-245. DAI H L, The asymptotic property of approximation to |x| by Newman-type rational operators at the two kinds of Chebyshev nodes [J].JournalofChinaUniversityofMetrology, 2006, 17(3) :243-245.

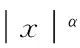
[11] BRUTMAN L , PASSOW E. On rational interpolation to |x| [J].ConstructiveApproximation, 1997,13(3) :381 -391.

[12] ZHU L Y, DONG Z L. On Newman-type rational interpolation to |x| at the Chebyshev nodes of the second kind[J].AnalysisinTheoryandApplications, 2006, 22(3) :262-270.

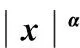
CHENG Yiyuan1, ZHANG Yongquan1, FEI Jingtai2

(1.College of Sciences, China Jiliang University, Hangzhou 310018, China;
2.School of Mathematics and Computation Sciences, Anqing Normal University, Anhui Anqing 246133, China)

2096-2835(2017)03-0404-05

10.3969/j.issn.2096-2835.2017.03.022

2017-06-19 《中国计量大学学报》网址zgjl.cbpt.cnki.net

国家自然科学基金资助项目(No.11301494，61573326).