小波特征和协同表示的步态识别研究

王鹏峰，程 铭

(中国计量大学 计量测试工程学院，浙江 杭州310018)

小波特征和协同表示的步态识别研究

王鹏峰，程 铭

(中国计量大学 计量测试工程学院，浙江 杭州310018)

提出一种步态能量图(Gait Energy Image,GEI)的Gabor小波特征与协同表示的步态识别算法.首先通过运动目标检测, 二值化和形态学处理等预处理操作得到步态轮廓图，然后进一步从步态轮廓图计算得到步态能量图. 该算法将步态能量图的Gabor特征作为特征矢量，采用协同表示的方法进行步态识别.在实验阶段，通过在中科院自动化研究所CASIA步态数据库的Dataset B上进行测试，证明上述算法具有运行速度快的优点，并且对于跨视角步态识别具有一定的鲁棒性.

Gabor小波；步态能量图；协同表示

Abstract: A gait recognition algorithm based on Gabor wavelet feature of GEI and collaborative representation was proposed. The detected moving target was processed with binarization and morphological precessing to get the gait contour map and calculate the gait energy image. The algorithm represented the gait recognition by using the collaborative method with Gabor gait energy image as the feature vector. In the experimental stage, tested by the Chinese Academy of Sciences Institute of Automation CASIA Dataset B gait database, it shows that the algorithm has the advantages of fast operation speed, and is robust to cross view gait recognition.

Keywords: gabor wavelets; GEI; cooperative representation

生物特征识别技术因具有简洁快速和安全高效的优点在信息安全中扮演着重要的角色，是现阶段既便捷又安全的身份认证方法.步态识别主要按照人行走时的步态特征来对身份识别，由于它具有非接触和隐蔽性等特点，被广泛应用在视频监控等领域.

Niyogi和Adelson[1]是最早把步态特征应用到对人的身份检测识别中，Nixon等[2]从理论角度证实了利用步态特征进行身份识别具有可行性.Yam等[3]利用钟摆模型描述腿部的运动情况，并采用改进的傅里叶系数对其进行特征提取.Hayfron-Acquah等人[4]创新性地提出了基于人体对称性的步态识别方法.上述基于模型的步态识别方法都需要获取轮廓清晰的步态序列，会导致模型构建过程的时间复杂度相对较高.而基于非模型的方法主要侧重于提取人行走时侧面的形态，将提取人体目标移动时侧面的形态作为特征.与基于模型的方法相比，基于非模型的方法并不需要对整个人体或者人体的某个部分建模，非模型的方法对人体侧影图不敏感而且计算复杂度较低.研究人员主要用基于非模型的方法进行步态识别，Bashir[5]选取GEn步态熵图作为步态特征并识别.2005年，Han[6]等人首次提出了步态能量图的概念，并将其应用到步态识别中，取得了较高的识别率.

本文提出了一种基于Gabor小波和协同表示的步态识别算法.在中国科学院提供的步态数据库上进行了相关实验，实验结果表明，通过在CASIA步态数据库的Dataset B上进行测试，实验结果表明算法具有运行速度快的优点，并且对于跨视角步态识别具有鲁棒性.

1 步态特征选择与提取

1.1 基于步态能量图的Gabor特征

David Gabor于1946年提出了Gabor滤波器，并发现其可以很好地模拟人类视觉细胞感受野，捕捉突出的视觉属性(空间定位和方向选择)，可以提取到图像的多尺度以及多方向的特征.Gabor滤波器已被广泛应用在皮肤纹理类生物特征识别中并取得了不错的识别效果，文献[7]将在人脸识别中提取了局部人脸的Gabor特征，文献[8]将在虹膜的特征提取中应用了Gabor滤波器，文献[9]提取了指纹的Gabor特征.正是因为Gabor滤波器能够有效地提取图像多尺度和多方向的局部特征，因此本文拟将提取基于步态能量图的Gabor特征.

二维Gabor滤波器定义如下：

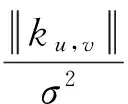
(1)

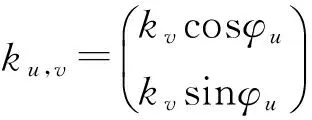
(2)

式(1)中,z=(x,y)表示输入步态图像某个像素点的空间坐标值，ku,v表示Gabor的中心频率，φu表示二维Gabor的方向性.exp(iku,vz)是复指数函数，实部为cos(ku,vz)，表示一个余弦平面波；虚部是sin(ku,vz)，表示一个正弦平面波.

二维Gabor小波的复数形式，其实部和虚部分别如式(3)和(4):

(3)

lm(ψu,v(z))=

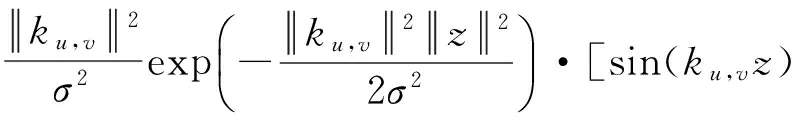
(4)

图1显示了步态能量图通过Gabor变换后5个尺度和8个方向上的图像.

图1 步态的Gabor特征Figure 1 Gabor feature of gait

将输入的步态图像和式(1)定义的二维Gabor小波进行卷积计算.这里假设步态图像为I(z)，该步态图像和二维Gabor小波卷积运算定义如式(5)所示.

Ou,v(z)=I(z)*ψu,v(z).

(5)

这里，*表示卷积算子，u∈{0,1,…,7}，v∈{0,1,…,4}，当尺度v和方向u确定以后，Ou,v(z)表示Gabor核函数的卷积图像.由于二维Gabor小波的特性，步态图像经过Gabor小波变换之后得到一组Gabor图像，表示为S={Ou,v(x,y)∶v∈(0,1,…,4),u∈(0,1,…,7)},这40个特征表示的是图像在以每个位置为中心的周边区域能量分布.Jz表示将40个特征级联后的结果，即步态图像的Gabor特征，如式(6):

(6)

将所有像素对应的Jet级联起来，得到一副步态图像的特征向量，步态图像I(x,y)的Gabor特征向量如式(7)所示.由于Gabor小波提取后的特征维数是输入步态图像的40倍，这将会有一定的计算开销.因此，需要对初次得到的步态特征进行降维处理.

T={Jz(x,y)|(x,y)∈I} .

(7)

1.2 步态特征降维

本文采用主成分分析法(PCA)和线性判别分析法(LDA)[10]相结合的方法对步态能量图进行降维，降维后获得的矩阵即为我们需要的步态特征.

PCA和LDA进行特征提取的流程如下：

1) 采用主成分分析法(PCA)对步态能量图降维，得到变换矩阵Wpca.

2) 将PCA降维后的数据进行线性判别分析(LDA)，求得最佳的分类子空间和变换矩阵Wlda；下面详细介绍求解变换矩阵的过程.

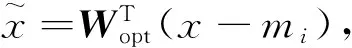
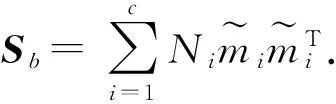
⑤计算特征值和特征向量SbV=λSwV.从PCA特征子空间到线性判别分析子空间的变换矩阵则为Wlda=[v1,v2,…,vc-1];

⑥计算投影矩阵：wopt=wpca·wlda.

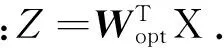
本文利用PCA对原始数据进行降维(累计贡献率设置为95%)，然后通过LDA使降维后的特征投影到具有良好分类性质的特征子空间，从而形成具有良好分类性能的特征.

2 Gabor特征与协同表示的步态分类算法

2.1 基于稀疏表示的步态分类识别算法

步态测试样本y的类别归属信息可以由矢量L(ω,b,α)中的稀疏非零值得到.

SRC算法流程如下：

1)将训练集X中列矢量归一化，使得每一个列矢量的l2范数为1.

2)将测试样本y基于X进行稀疏编码，通过式(9)的l1范数最小化的方法.

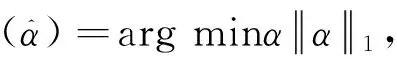
(9)

其中，常数L(ω,b,α)表示y和稀疏矢量ω的编码误差.

(3)计算残差

(10)

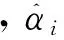
(4)测试样本y归属类别

identity(y)=arg mini{ei}

.

(11)

2.2 基于协同表示的步态识别算法

在步态识别中，每一类步态图像都在Rm的子空间中，即m维的步态图像可以用维数更低的特征矢量表示.若将第i类训练样本的集合Xi作为这一类的字典，则Xi中的训练样本是相关的;如果训练样本的数量较多，则属于第i类的图像完全能够通过Xi来表示，即属于第i类的样本y可以通过Xi稀疏地表示.通过上述分析可知，稀疏表示算法需要足够多的训练样本，使得Xi满足超完备的要求.而在实际应用中，步态识别属于小样本问题，导致Xi是非完备的.假设用非完备的Xi来表示y，则会引起较大的误差并使得最后的分类结果不稳定.

协同表示的核心思想是利用所有类的训练样本表示或编码测试样本，考虑了所有样本之间的合作.对于步态识别的应用而言，不同类别的GEI具有一定的相似性，即第j类的GEI有助于表示第i类的测试样本.从三个人的步态能量图可以看出，肢体的摆动频率和轮廓特征都很相似，不同人的GEI之间存在着一定的相关性.在稀疏表示算法中，基于l1范数的稀疏性约束条件下，测试步态样本y可以用所有训练样本X=[X1,X2,…,XK]协同表示.文献[11]将协同表示应用到人脸中并论证了稀疏表示算法主要取决于内在数据样本之间的协同表示，而并非l1范数的稀疏性，因此得出结论，将l1范数的稀疏性约束条件简化为最小二乘约束问题.

2.3 本文算法

为了提高算法的准确性和鲁棒性，本文基于GEI提取其多尺度和多方向的Gabor特征，并运用PCA与LDA相结合的方式对提取到的Gabor特征进行降维，在识别阶段采用协同表示进行识别，提出了一种基于步态Gabor特征和协同表示的步态分类算法.

假设第i类步态样本提取的Gabor特征为Xi=[xi,1,xi,2,…,xi,ni]，则所有步态训练样本的Gabor特征为X=[X1,X2,…,XK].根据协同表示的思想，利用训练样本的特征对测试样本进行协同表示，将稀疏表示算法l1范数稀疏性的约束条件简化为规则化的最小二乘法，将(12)式简化为

(12)式(12)中的ρ表示系数矢量，λ表示规则化参数，与稀疏表示的算法相比，协同表示的算法求解规则化最小二乘问题要比l1范数的最优化问题更加简单，(12)式中协同表示方法的最优解为

(13)

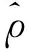
2.4 算法流程

2.4.1步态训练步骤

1)首先将每个训练样本的Gabor特征按列展开成列向量，将所有训练样本组成字典X=[X1,X2,…,Xn]，字典中Xi表示第i类训练样本组成的集合，每一列表示训练样本数据；

2)X按列进行规范化得到单位l2范数；

3)采用主成分分析法和线性判别分析法相结合的方式对字典X进行降维；

4)计算投影矩阵P，其中，

P=(XTX+λI)-1XT.

2.4.2 步态识别步骤

1)首先将步态测试样本按列展开为列向量并规范化；

2)将测试样本采用主成分分析法和线性判别分析法相结合的方式降维；

3)对每一测试样本y,计算y在投影矩阵P上的投影ρ=Py；

4)计算规则化残差

(14)

5)输出最终的识别结果(将y归为残差最小的类)

identity(y)=arg mini(ri).

(15)

3 实验结果与分析

本文实验是在CPU 3.35 GHz，内存8.00 GB，MATLAB R2014a环境下实现的，在CASIA步态数据库Dataset B上进行实验，并用Matlab对算法进行编程实现.本文选取的正则化参数xixj为0.001.首先随机选用124个人中的24个人在90°视角下的图像序列，每个人包含两个背包行走序列(数据集A)，两个穿大衣行走序列(数据集B)和六个正常行走序列(数据集C)，进行10次实验.将每个人A和B的前一组步态序列作为训练集，剩下的一组步态序列作为测试集.正常行走序列(数据集C)的前三个步态序列作为训练集，剩下的三个序列作为测试集，本文选用的评价指标是平均识别率(Average Recognition Rate，ARR)，即：

(16)

本文算法首先与最近邻分类算法(NN)，稀疏表示算法(SRC)[12]进行识别率的比较，识别率和识别时间如表1和表2.

从表1可以看出，由于本文算法和基于稀疏表示的算法(SRC)采用了协同表示的思想，与最近邻算法(NN)相比，识别率有了明显的提高.从表2的识别时间来看，本文算法明显快于稀疏表示算法(SRC)，主要原因是投影矩阵P在测试前可以被计算出来，在测试过程中，对于输入的测试样本y可以快速构造出重构系数，而稀疏表示(SRC)算法相对耗时的原因是对于输入的测试样本y都需要计算l1范数，随着测试样本数的增多，计算的时间也会增加.与最近邻算法相比，由于需要在步态能量图的基础上提取其多尺度和方向的Gabor特征，需要耗费一定时间，因此要比最近邻算法(NN)稍慢一些.

为了验证本文算法对多视角的鲁棒性，实验以90°视角和126°视角下三种状态下124个人的步态序列为训练集，其余四个视角下的步态作为测试集进行跨角度验证.并与近年来的文献进行了比较，实验的识别率如表3和表4.从表3和表4可以看出，在考虑跨视角的情况下，本文算法与其他五种算法相比，仍然取得了很好的识别效果.主要原因是对于不同角度下的步态能量图具有很强的相似性，比如90°视角下的GEI和72°，108°视角下的GEI在高能量部分和肢体的摆动频率都具有一定的相似性，而协同表示正是强调了样本之间的合作，使得本文算法对跨角度实验有一定的鲁棒性.

表1NN,SRC和本文算法的识别率

Table 1 Recognition rate of NN,SRC and proposed algorithm%

表2NN、SRC和本文算法的识别时间

Table 2 Rrecognition time of NN,SRC and proposed algorithms s

表3六种算法在四个不同视角测试的识别率(训练集为90°)

Table 3 Rrecognition rate of the six algorithms tested at four different angles of view(Trainning set at 90°)

测试集角度72°108°126°144°FG+SVD[13]0.400.450.200.20GEI+LDA+TSVD[14]0.700.720.100.20自校准法[15]0.700.680.16-Yu的方法[16]0.810.870.220.03文献[17]0.970.930.56-本文算法0.980.950.600.32

表4六种算法在四个不同视角测试的识别率(训练集为126°)

Table 4 Recognition rate of the six algorithms tested at four different angles of view(Trainning set at 126°)

测试集角度72°108°126°144°FG+SVD[13]0.290.480.600.40GEI+LDA+TSVD[14]0.430.720.890.48自校准法[15]0.590.600.70-Yu的方法[16]0.680.820.480.03文献[17]0.550.800.73-本文算法0.710.900.940.28

4 结 语

本文在以步态能量图作为特征的基础上，提出了一种基于步态能量图的Gabor特征和协同表示的步态识别算法，采用协同表示的方法进行步态识别,对跨角度实验有一定的鲁棒性，是一种有效的步态识别方法.

[1] NIYOGI S A, ADELSON E H. Analyzing and recognizing walking figures in XYT[C]//IEEEComputerSocietyConferenceonComputerVisionandPatternRecognition. USA:IEEE，1994:469-474.

[2] NIXON M S, CARTER J N, CUNADO D, et al. Automatic gait recognition[J].Biometrics, 1996, 7(2):231-249.

[3] YAM C Y, NIXON M S, CARTER J N, et al. Automated person recognition by walking and running via model-based approaches[J].PatternRecognition, 2004, 37(5):1057-1072.

[4] HAYFRON-ACQUAH J B, NIXON M S, CARTER J N, et al. Automatic gait recognition by symmetry analysis[J].PatternRecognitionLetters, 2003, 24(13): 2175-2183.

[5] BASHIR K, XIANG T, GONG S, et al. Gait recognition without subject cooperation[J].PatternRecognitionLetters, 2010, 31(13):2052-2060.

[6] HAN J, BHANU B.Individual recognition using gait energy image[J].IEEETransactionsonPatternAnalysis&MachineIntelligence, 2006, 28(2):316-322.

[7] WANG N, LI Q, EL-LATIF A A , et al. An enhanced thermal face recognition method based on multiscale complex fusion for Gabor coefficients[J].MultimediaToolsandApplications, 2014, 72(3): 2339-2358.

[8] RADMAN A, JUMARI K, ZAINAL N, et al. Fast and reliable iris segmentation algorithm[J].IetImageProcessing, 2013, 7(1): 42-49.

[9] KHAN T M, KHAN M A U, KONG Y,et al. Fingerprint image enhancement using multi-scale DDFB based diffusion filters and modified Hong filters[J].Optik-InternationalJournalforLightandElectronOptics, 2014, 125(16): 4206-4214.

[10] FISHER R A. The use of multiple measurements in taxonmic problems[J].Annalsofeugenics, 1936, 7(2):179-188.

[11] ZHANG L, YANG M, FENG X, et al. Sparse representation or collaborative representation: Which helps face recognition?[C]//2011InternationalConferenceonComputerVision.Barcelona,Spain： IEEE, 2011: 471-478.

[12] 杨旗, 薛定宇, 崔建江. 基于稀疏表示的步态识别[J]. 东北大学学报(自然科学版), 2012, 33(1): 43-46. YANG Q，XUE D Y，CUI J J.Gait recognition based on sparse representation[J].JournalofNortheasternUniversity(NatualScienceEdition),2012,33(1):43-46.

[13] MAKIHARA Y, SAGAWA R, MUKAIGAWA Y, et al. Gait identification using a view transformation model in a frequency domain[J].CVIM2006, 2006(5): 117-124.

[14] KUSAKUNNIRAN W, WU Q, LI H, et al. Multiple views gait recognition using View Transformation Model based on optimized Gait Energy Image[C]//IEEEInternationalConferenceonComputerVisionWorkshops. Kyoto：IEEE，2009: 1058-1064.

[15] GOFFREDO M, BOUCHRIKA I, CARTER J N, et al. Self-calibrating view-invariant gait biometrics[J].IEEETransactionsonSystems,Man,andCybernetics, 2010, 40(4): 997-1008.

[16] YU S, TAN D, TAN T,et al. A framework for evaluating the effect of view angle, clothing and carrying condition on gait recognition[C]//18thInternationalConferenceonPatternRecognition. Hong Kong: IEEE, 2006: 441-444.

[17] KUSAKUNNIRAN W, WU Q, ZHANG J, et al. A new view-invariant feature for cross-view gait recognition[J].InformationForensics&SecurityIEEETransactionson, 2013, 8(10):1642-1653.

Researchongaitrecognitionofwaveletandcooperativerepresentation

WANG Pengfeng, CHENG Ming

(College of Metrology and Measurement Engineering, China Jiliang University, Hangzhou 310018, China)

2096-2835(2017)03-0359-06

10.3969/j.issn.2096-2835.2017.03.015

2017-06-28 《中国计量大学学报》网址zgjl.cbpt.cnki.net

TP391.41

A