二次指数平滑法优化马尔科夫预测模型

吕丹丹，顾巧祥，邢 超

(中国计量大学 质量与安全工程学院，浙江 杭州310018)

二次指数平滑法优化马尔科夫预测模型

吕丹丹，顾巧祥，邢 超

(中国计量大学 质量与安全工程学院，浙江 杭州310018)

马尔科夫预测模型具有“无后效性”，即预测未来的销售情况只与当前的销售数据有关，而与过去的销售数据无关.事实上，过去不同的时间点对当前的销售结果会有不同程度的影响.而指数平滑法恰好弥补了马尔科夫预测模型的缺点，它认为最近的过去销售数据，在某种程度上会持续到未来.因此本文利用二次指数平滑系数法优化马尔科夫预测模型，并以某品牌电动车的销售情况为例进行验证，发现优化后预测模型的绝对误差均小于马尔科夫模型的预测结果.由此得出结论，基于二次指数平滑法优化的马尔科夫预测模型具有可行性.

马尔科夫链；状态转移概率；二次指数平滑法；销售预测

Abstract: Markov has “no aftereffect”, which means that future sales will only be related to the current sales data, not to the past sales figures. In fact, different time points in the past have different degrees of impact on current sales results. The exponential smoothing, which makes up for the shortcomings of the Markov prediction model, suggests that recent past sales data, in some ways, will influence the future. In this paper, the quadratic exponential smoothing coefficient method is used to optimize the Markov prediction model, and is verified with some brand electric car sales. It was found that the absolute error of the optimized prediction model was less than the predicted results of Markov models. Therefore, it is concluded that the Markov prediction model based on the quadratic exponential smoothing method is feasible.

Keywords: Markov Chain; transition probability matrix; secondary exponential smoothing; sales forecast

马尔科夫链，因安德烈·马尔科夫(A.A.Markov,1856-1922)得名，是指数学中具有马尔科夫性质的离散时间随机过程.该过程中，在给定当前知识或信息的情况下，过去(即当前以前的历史状态)对于预测将来时无关.因此，马尔科夫链可用来对现实中的许多具有无后效性特点的事物进行预测.国内外众多学者应用马尔科夫链进行了各种研究和预测，张浩[1]，刘爱红[2]等人在医药方面应用马尔科夫链预测药物转运时间及评价药物经济性；张家善[3]等人应用马尔科夫链预测了港口的吞吐量情况；钟国敏[4]等人应用马尔科夫链分析研究了土地利用的动态演变情况.随着马尔科夫模型的不断发展，更多的学者将其与其他数学理论结合应用，使马尔科夫模型的预测结果更加精准.刘春月[5]在预测物流需求时，用灰色模型对马尔科夫预测得到的结果进一步分析研究，发现最终的预测精度比单一的预测精度有很大的提高；文士发[6]提出了一种新的计算转移概率的方法来改进马尔科夫链预测模型，经实例验证表明改进的模型比原模型的预测精度更高.目前，马尔科夫模型的发展虽趋于成熟，但仍存在不足.在预测过程中，其预测结果只与当前的数据及状态转移概率矩阵相关，忽略了历史数据的影响.因此，本文的研究目的是为了能够得到更好的预测精度，引入二次指数平滑法优化马尔科夫链的预测模型，使得历史数据对预测结果具有一定的影响.

1 马尔科夫链的预测模型

1.1 马尔科夫链的定义

假设马尔科夫过程{Xn，n∈T}的参数集T是离散的时间集合，即T={0，1，2，…},其相应Xn可能取值的全体组成的状态空间是离散的状态集I={i0,i1i2…}.若随机过程{Xn，n∈T}对于任意的非负整数n∈T和任意的i0，i1，i2…in+1∈I，其条件概率满足：P={Xn+1=in+1|X0=io，X1=i1，…，Xn=in}=

{Xn+1=in+1|Xn=in}.

(1)

则称{Xn，n∈T}为马尔科夫链，简称马氏链.

1.2 状态转移概率

条件概率P{Xn+1=j|Xn=i|}的直观含义为系统在时刻处于状态的条件下，在时刻n+1系统处于状态的概率.记此条件概率

Pij(n)=P{Xn+1=j|Xn=i}

(2)

为马尔科夫链{Xn，n∈T}在时刻n的一步转移概率，简称转移概率，其中i,j∈I.

一般地，计算转移矩阵步骤如下：

(1)对原始数据分组，即数据离散化.

(2)计算初始概率.假设时间序列

X={x1,x2,…,xn}.

有n个观测值，其中Xn未知.被划分为r个状态.

E={e1,e2,…,er}.

若有ci数据落在ei中(∑ci=n-1),则状态发生的概率为

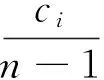
(3)

(3)计算一步转移概率.落在中的数据有ci个，下一时刻转移到ei的数据有cij,所以ei一步转移到ej的转移概率为

(4)

1.3 马尔科夫预测模型

已知初始状态概率S(t)以及一步转移状态概率p，则下一状态的马尔科夫预测值为

S(t+1)=S(t)·P.

(5)

同理，后期的预测值为：

S(t+2)=S(t)·P2，

S(t+n)=S(t)·pn.

(6)

2 指数平滑法

指数平滑法(exponential smoothing,ES)是布朗(Robert G.Brown)提出.布朗认为时间序列的态势具有稳定性或规则性，所以时间序列可被合理地顺势推延；他认为最近的过去态势，在某种程度上会持续到未来，所以将较大的权数放在最近的资料.

根据平滑次数的不同，指数平滑法分为：一次指数平滑法、二次指数平滑法及三次指数平滑法，他们的区别如表1.

表1三种指数平滑法的区别

Table 1 Difference between three exponential smoothing methods

区别一次指数平滑法二次指数平滑法三次指数平滑法发展趋势无明显的趋势变化具有线性趋势变化二次曲线趋势变化

本文主要针对的是对制造业产品进行预测，所以产品的发展趋势是根据现有的科技手段呈线性趋势在逐渐提高的，因此选择二次指数平滑法进行后期的计算.

2.1 二次指数平滑法

当数据从某时期开始具有直线趋势，且认为未来时期会按此直线趋势变化的时候，用一次指数平滑法就不能得到较好的预测结果，会有滞后偏差.这时对依次平滑进行修正，即再做一次指数平滑，称之为二次指数平滑.计算公式如下：

(7)

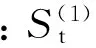
2.2 指数平滑系数α的确定

在指数平滑法预测中，α即指数平滑系数的确定对整个精度有着非常重要的影响.α越大，距离预测状态越近的数据占有的成分越大.从理论角度看，α的取值范围在0～1之间，选取原则是预测误差越小，精度越高.

本文拟借助excel求解α(0<α<1)的值.在excel中有数据分析工具——指数平滑法确定这一选项，首先随机选取不同的α值，并计算各值对应的绝对误差，根据误差越小α值越优为原则缩小α值的选取范围；随后对在范围内随机选取α值，再比较绝对误差，以此类推(一般α值精确到百分位或十分位即可)；最后绝对误差值最小者即为最优α值.

3 基于二次指数平滑法的马尔科夫预测模型

3.1 模型概述

在运用历史数据预测下一状态发展趋势时，不考虑各时间段对预测结果的权重问题，可能会导致预测结果误差偏大的现象.而二次指数平滑法，可以根据与当前时间的远近进行加权运算，使得距离当前越近的数据，对预测值的影响愈大;反之，距离当前时间越远的数据，对预测结果影响越小.所以，本文将二次指数平滑法与马尔科夫链这两种预测方法相结合，提出一种改进的马尔科夫链模型.

在改进的马尔科夫链模型中，使用当前状态以及与当前状态紧邻的两个历史状态的加权和来预测下一个状态.权重的分配采用二次指数平滑法，按其原则依时间从近到远，权值呈指数递减.具体公式如下：

α(1-α)2St-2P3.

(8)

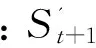
对公式(8)进一步变换，可得

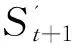
(9)

3.2 模型算法描述

综上所述，采用改进后的马尔科夫模型预测下一状态的计算流程如图1.

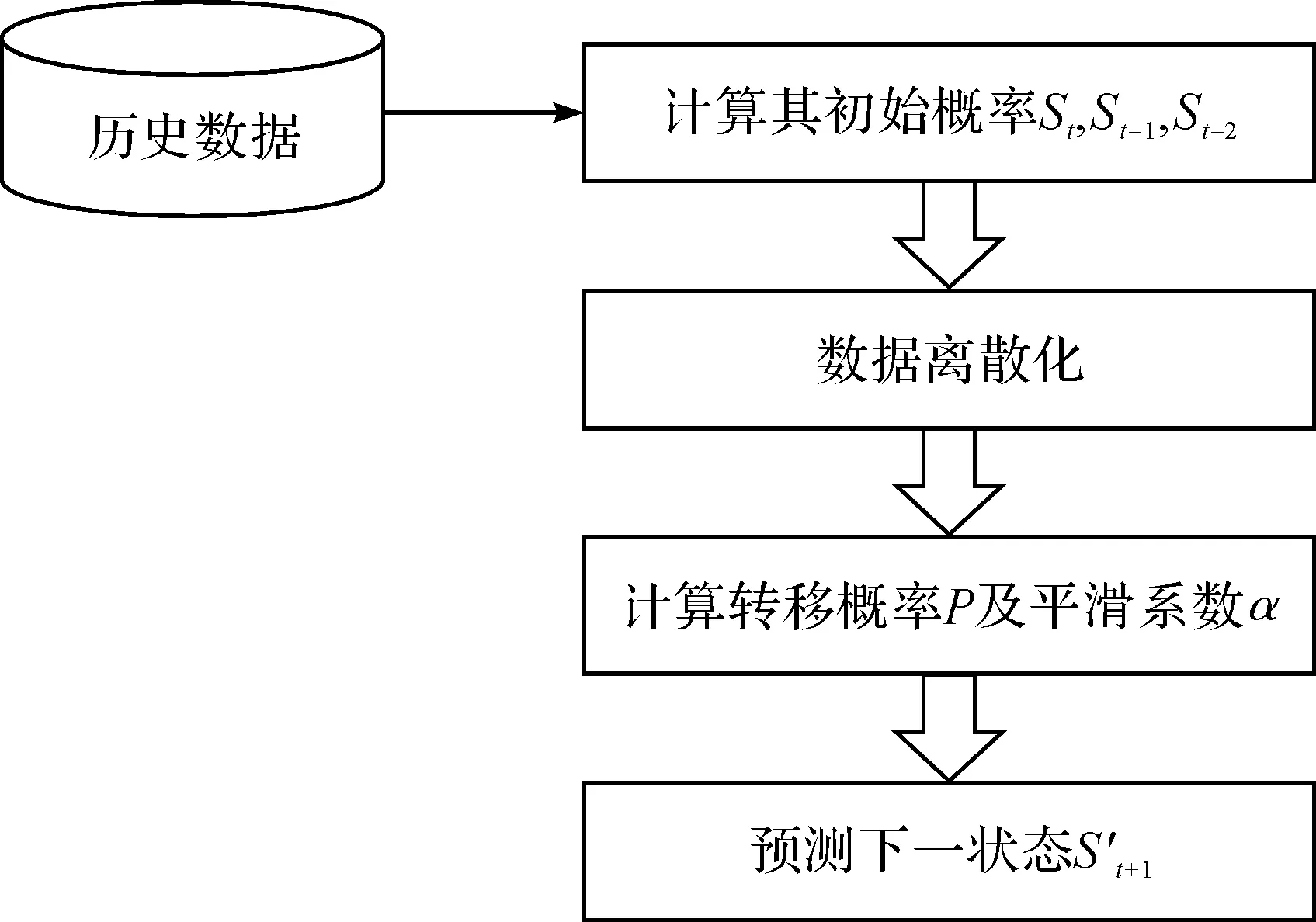
图1 改进的马尔科夫模型预测下一状态的流程图Figure 1 Improved Markov model predicts the flow chart of the next state

其中，数据离散化实际上就是根据某种相似性或者相异性对数据进行分类.

4 实例验证

基于以上对模型的描述，本文将借助excel和matlab工具分别来确定α值以及求解最终的预测值.下面以预测某新艺电动车零售店的销售情况为例，来验证本文提出模型的有效性.

每个品牌的电动车通常会根据其性能或外观等不同，生产不同系列的子产品以应对市场的不同的需求.例如华为手机，其旗下拥有荣耀系列、mate系列及P系列等不同的子产品，为应对不同的消费群体、不同的用户需求.新艺电瓶车根据不同的用户需求，生产不同的车型来供不同人群使用，主要有电动摩托车和电动三轮车，而电动摩托车又分为豪华款、简约款、一度宽频等系列，每个系列又会根据配置的不同进行细分.本文主要以新艺电动车旗下的豪华款系列中的战威、战影、战迪、战神等12种款式为依据，在已知某零售店2016年1-11月份的实际销售情况，来预测12月份该12种款式销售的概率情况.

已知2016年1-11月份该零售店销售12种电动摩托车共115辆，统计各月份的各状态数，建立状态空间，如表2.

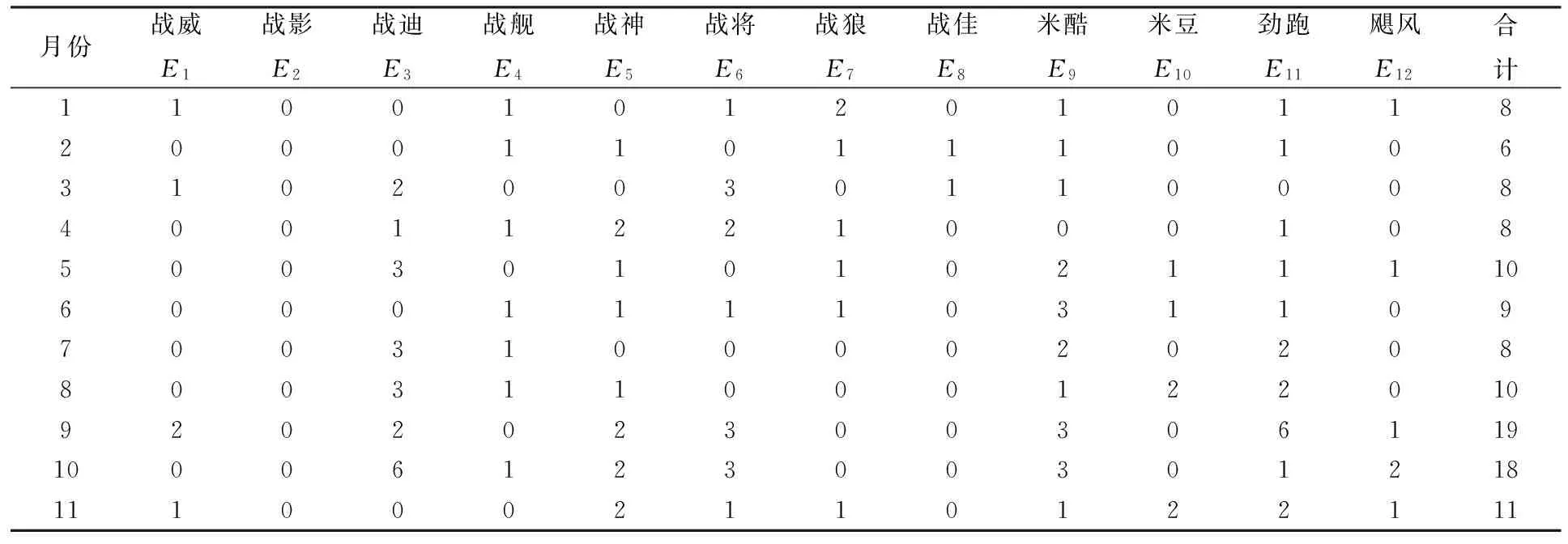
表2 2016年1-11月份的各状态数统计

其次根据已有的状态空间及式(3)可以计算各个状态的初始概率S0：

然后，根据式(4)计算出各状态一步转移概率：

同时，在excel中运用指数平滑数据分析，通过选取不同的α值，来比较预测值与真值间的绝对误差大小，误差越小者，则其对应的α值为最优.通过最终结果比较，可以得到，当α=0.99时，绝对误差最小，因此，选取此α值作为最终指数平滑系数.

最后，根据公式(5)和(8)分别求解2016年9至11月份马尔科夫模型预测值及基于二次指数平滑法优化的马尔科夫模型预测值(如表3、表4)，并与真值作比较(表格中的误差为绝对误差)，分析优化后的模型精度是否更好.

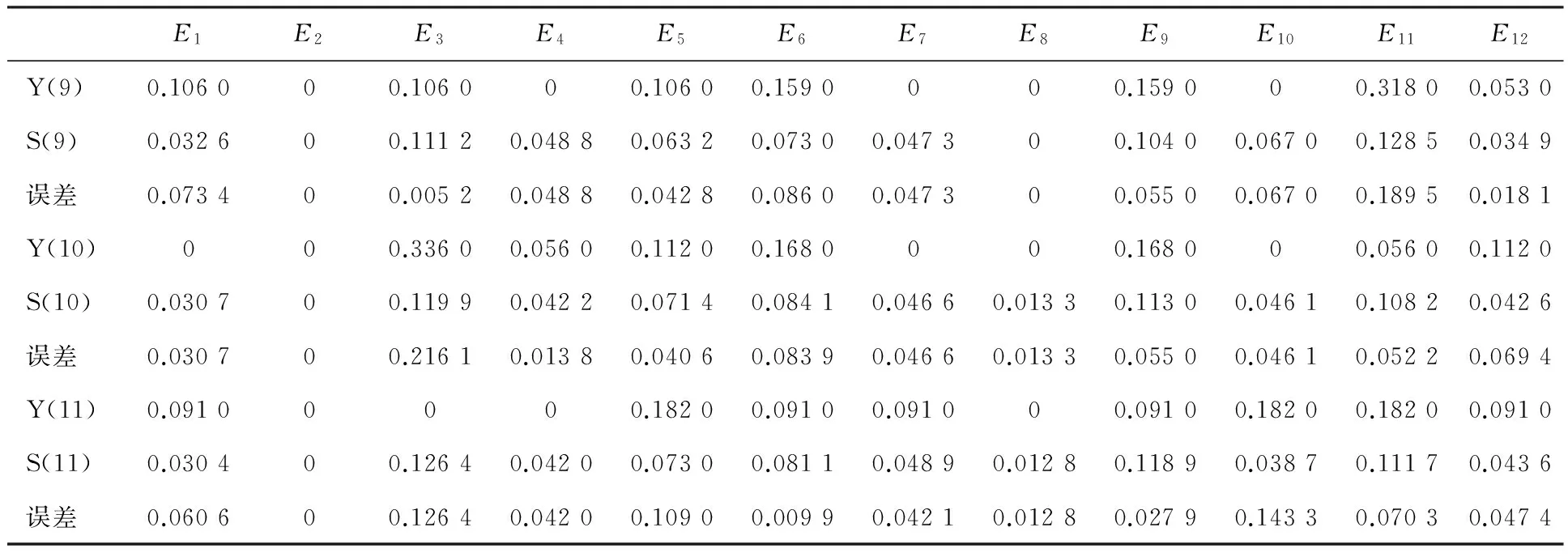
表3 2016年9-11月份马尔科夫模型预测值

由表3可求得9月、10月及11月的平均绝对误差，分别为5.28%、5.60%、5.76%.

表42016年9～11月份基于二次指数平滑法的马尔科夫预测值

Table 4 Markov forecast based on the second exponential smoothing method in September and November 2016

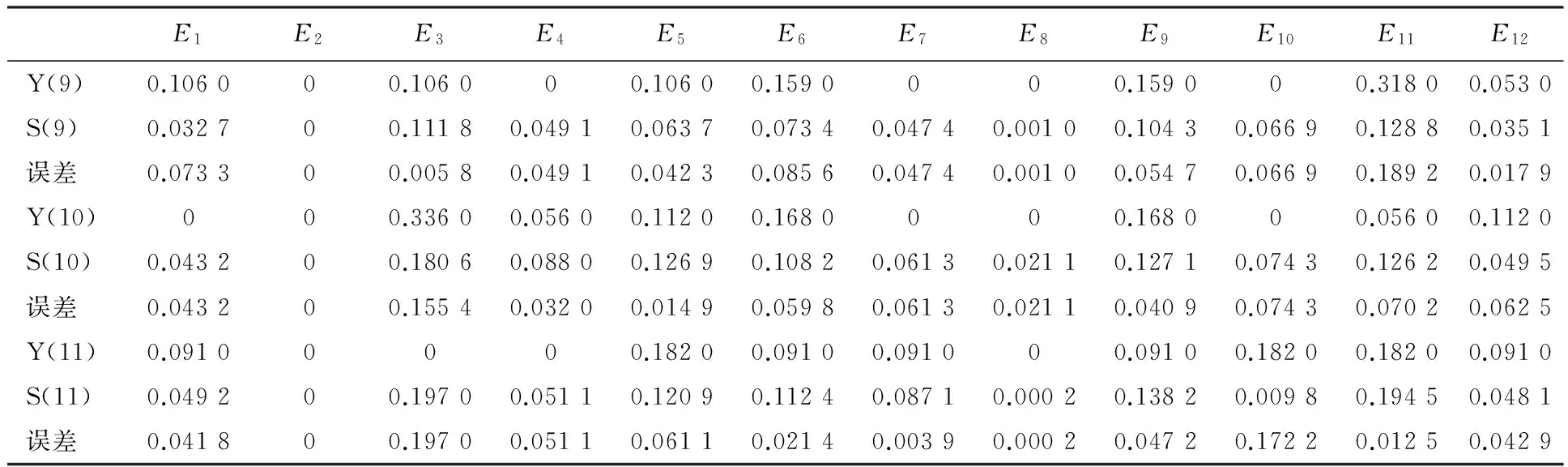
E1E2E3E4E5E6E7E8E9E10E11E12Y(9)0.106000.106000.10600.1590000.159000.31800.0530S(9)0.032700.11180.04910.06370.07340.04740.00100.10430.06690.12880.0351误差0.073300.00580.04910.04230.08560.04740.00100.05470.06690.18920.0179Y(10)000.33600.05600.11200.1680000.168000.05600.1120S(10)0.043200.18060.08800.12690.10820.06130.02110.12710.07430.12620.0495误差0.043200.15540.03200.01490.05980.06130.02110.04090.07430.07020.0625Y(11)0.09100000.18200.09100.091000.09100.18200.18200.0910S(11)0.049200.19700.05110.12090.11240.08710.00020.13820.00980.19450.0481误差0.041800.19700.05110.06110.02140.00390.00020.04720.17220.01250.0429

由4可求得9月、10月及11月的平均绝对误差，分别为5.27%、5.29%、5.43%.

综上所述可以发现，基于二次指数平滑法优化的马尔科夫预测模型的预测结果精度更高.因此，采用新模型预测新艺电动车旗下品牌各状态12月份的分布情况，如表5.

表5 2016年12月份基于二次指数平滑法的马尔科夫预测值

预测结果表明，12月份最畅销的三款分别为E3、E6、E11，即战迪、战将和劲跑，所占比重分别为13.74%、10.65%及11.61%.因新模型的有效性，所以预测结果能够为零售店提供一定的销售依据，使零售商提前应对市场，做好准备.

5 总 结

本研究将二次指数平滑法引入到马尔科夫预测模型中，二次指数平滑法的核心理论是最近的过去态势，在某种程度上会持续到未来，所以将较大的权数放在最近的资料；而马尔科夫链最重要的性质是在给定当前知识或信息的情况下，过去(即当前以前的历史状态)对于预测将来时是无关的.因此，结合二者的优点，使两种方法在预测功能上得到互补，从而提高了预测的精度.本文提出的模型主要应用于制造业领域，不仅可预测其最终产品的销售情况还可以预测在制造过程中零部件的使用情况.但不论是马尔科夫预测模型还是二次指数平滑系数法，二者均适用于短期预测，因此该模型也主要适用于短期预测.文中最后以电动车为例的验证结果表明，基于二次指数平滑法优化马尔科夫预测模型达到了预期结果，起到了优化的作用，同时验证了新预测模型的可行性，今后还可将其应用于其他领域预测，以更好地满足用户需求.

[1] 张浩，黄泰康．药物经济学评价中马尔可夫模型的优化——马尔可夫决策模型[J]．药物经济学，2008，19(17): 1284-1286.ZHANG H，HUANG T K．An optimization of Markov model in the evaluation of drug economics:Markov decision model [J]．PharmaceuticalEconomics，2008，19(17) ：1284-1286．

[2] 刘爱红，杨光．应用马尔科夫链计算药物运转时间和稳态药量[J]．沈阳师范大学学报，2016，34(1)：57-61． LIU A H，YANG G．Use Markov chain to calculate the operation time and steady state medicine [J]．JournalofShenyangUniversity，2016，34(1)：57-61．

[3] 张家善，林晓群．基于马尔科夫链的港口吞吐量区间预测模型研究[J]．数学的实践与认识，2016，46(15)：159-164． ZHANG J S，LIN X Q．Based on Markov chain's port throughput interval prediction model research [J]．JournalofMathematicsinPracticeandTheory，2016，46(15)：159-164．

[4] 钟国敏，张学雷，段金龙．利用马尔科夫过程预测郑州市土地利用的动态演变[J]．河南农业大学学报，2011，45(6)：696-701． ZHONG G M，ZHANG X L，DUAN J L．The use of Markov process to predict the dynamic evolution of land use in Zhengzhou [J]．JournalofHenanAgriculturalUniversity，2011，45(6)：696-701．

[5] 刘春月．物流需求量灰色——马尔科夫链预测模型分析研究[J]．物流科技，2016(10) ：11-14． LIU C Y．Logistics demand gray ： Markov chain prediction model analysis and research [J]．LogisticsSCI-Tech，2016(10) ：11-14．

[6] 文士发，徐梅，王福林．一种估算马尔科夫状态转移概率矩阵的新方法[J]．数学的实践与认识，2014，44(8)：164-168． WEN S F，XU M，WANG F L．A new method of estimating Markov state transition probability matrix [J]．JournalofMathematicsinPracticeandTheory，2014，44(8)：164-168．

OptimizationonMarkovpredictionmodelswiththesecondexponentialsmoothingmethod

LYU Dandan, GU Qiaoxiang, XING Chao

(College of Quality and Safety Engineering, China Jiliang University, Hangzhou 310018, China)

2096-2835(2017)03-0334-06

10.3969/j.issn.2096-2835.2017.03.011

2017-06-29 《中国计量大学学报》网址zgjl.cbpt.cnki.net

浙江省自然科学基金资助项目(No.LY14E050024).

TP39

A