基于微分进化的EIT图像重建控制参数研究

刘 海，闫丹丹，荆会敏

(中国计量大学 信息工程学院，浙江 杭州310018)

基于微分进化的EIT图像重建控制参数研究

刘 海，闫丹丹，荆会敏

(中国计量大学 信息工程学院，浙江 杭州310018)

微分进化算法主要有三个随机参数：种群大小(NP),缩放因子(F),交叉因数(CR). 这些参数的取值对EIT图像重建效果的好坏起着重要的作用. 但当前微分进化算法参数选择具有随机性，大多数的参数研究是通过标准测试函数进行，没有具体到特定的领域. 针对这些问题，文章以头部EIT图像重建为例，在给定目标函数和终止条件的基础上，通过大量的仿真实验，分析了各个参数对图像重构结果的影响，并给出了这些参数的合理选取区间，从而为微分进化算法在EIT图像重建中的应用提供了有效的依据.

电阻抗成像；微分进化算法；有限元模型；参数设置

ControlparametersstudyofEITimagereconstruction

Abstract: Population size(NP), scaling factor (F) and crossover factor (CR) are the main random parameters of a differential evolution algorithm. The value of the parameters plays an important role in the EIT image reconstruction effect. However, the current parameter selection is random and nonspecific. To solve these problems, based on given objective functions and termination conditions, and a large number of simulation experiments of the head EIT image reconstruction, the influence of each parameter on image reconstruction was analyzed, and the reasonable selection interval of these parameters was given. It provides an effective basis for the application of differential evolution algorithms in EIT image reconstruction.

Keywords: electrical impedance tomography(EIT); differential evolution(DE) algorithm; finite element model; parameter setting

电阻抗断层成像(electrical impedance tomography, EIT)是现今国内外生物医学领域的重要研究课题之一，是一种非侵入性的无损功能性成像技术. 首先将对人体安全的交变电流注入到附着在被测组织表面的电极上，然后测量得到相应的边界电位，最后通过重构算法求解边界值问题，重构出被测组织内部的电阻率分布[1]. 与传统的医疗成像技术相比，EIT技术能在疾病发生初期检测到人体组织电阻率分布的变化，这有助于疾病的早期发现与诊断，并且可多次反复使用、无电离辐射[2]、成本相对较低、能长期对疾病进行监测和观察，因而具有较大潜力，应用领域十分广泛，是一种具有较大研究价值的医学成像技术[3-4].

EIT图像重构问题是一个高度病态的非线性逆问题. 国内外研究者提出了许多经典的图像重构算法，如修正牛顿-拉夫逊法、双限定法、剥层算法等. 目前修正的牛顿-拉夫逊法是最成熟的重构算法之一，应用十分广泛. 但此方法对初值的选择较为苛刻，一旦初值选择不当，则较易陷入局部最优，并且需进行恰当的正则化处理并计算雅克比矩阵，计算复杂，繁琐. 近来研究者逐渐将智能优化类算法(如神经网络算法、粒子群算法、遗传算法等)应用到EIT图像重构中，由于这些算法能直接对目标函数进行评价，无需求微分，对函数是否连续没有要求等优势而获得了广泛的应用[5].

微分进化(differential evolution, DE)是一种基于种群进化的全局启发式算法，易于实现[6]，控制参数较少，且在很多优化类的问题上都有优于其他算法的效果. DE算法的几个主要控制参数为：种群大小(NP)、交叉因数(CR)、缩放因子(F). DE性能对控制参数的选取非常敏感，但在DE中很难获得这些控制参数值的最佳组合，并且在不同的应用问题中需要不同的参数组合，所以需要大量反复的实验[7]. 研究表明，DE中动态参数控制有优于恒定参数控制的效果. 这些参数控制中的大多数是通过标准测试函数进行分析的，很少具体到特定的领域[6,8]. 因而EIT中DE算法的参数选取还没有严格的理论依据. 在本研究中，采用DE算法进行EIT图像重建，对影响图像重建质量和重建效率的DE算法的三个控制参数进行了详细的分析，同时对参数初始合理范围的选取给出了一些建议.

1 EIT原理

EIT图像重构理论上是一个低频电流场计算的逆问题. 通常忽略皮肤与电极间的接触阻抗，在EIT测量中激励源的频率较低，可将电流场看作稳态电流场. 场域内的电阻率分布函数ρ与电位分布φ由满足相应边界条件的拉普拉斯方程确定[9]：

▽·ρ-1(x,y)▽φ(x,y)=0 (x,y)∈Ω.

(1)

其边界条件为：

φ(x,y)=φ0(x,y) (x,y)∈∂Ω.

(2)

(3)

其中∂Ω为区域Ω的边界，ρ为目标内部电阻率分布，φ为场域内电位分布，φ0为已知的边界电位，n是区域边界外法线方向，j为流入区域的电流密度.

EIT正问题是在已知电阻率分布ρ以及激励电流模式j的情况下求解边界电位φ，而逆问题则是由已知边界处的φ0和j求解目标内部电阻率分布.

在正问题求解中，本实验通过有限元分析软件ANSYS进行建模、剖分，采用相对注入方式对模型注入安全电流，然后通过ANSYS“测量”出边界电位值；在逆问题求解中，DE算法通过不断地迭代求解使目标函数达到最小的电阻率分布，目标函数通常选为电位计算值与电位“测量”值之间残差的函数，其公式如下：

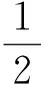
(4)

式中(·)T表示矩阵的转置，φ(ρ)是边界电位计算值，φ0是边界电位“测量值”.

2 DE算法

DE算法是一种基于群体的随机启发式搜索算法. 其基本思想是：首先由随机产生的初始种群开始，然后由父代个体间的变异操作产生变异个体，接着父代个体和子代个体之间按一定的概率进行交叉操作，生成实验个体，最后试验个体与父代个体之间依据目标函数值的大小进行贪婪选择操作，保留较优的个体，从而实现种群的进化. 其具体过程如下：

Step 1 种群初始化. DE算法一般采用随机函数产生NP个维数为D的初始种群xi,G，i= 1，2，…，NP，其中i表示种群个体序列号，G表示种群进化代数，NP表示种群规模.DE算法的初始种群是在给定边界约束内随机产生的，然后通过变异、交叉、选择等操作产生下一代种群.

Step 2 变异. 对第G代种群中的每个目标向量xi,G，根据生成变异向量方法的不同，能够组合成不同的变异策略，其中基本的变异策略DE/rand/1/bin方程为

vi,G+1=xr1,G+F·(xr2,G-xr3,G).

(5)

其中r1 ≠r2 ≠r3 ≠i，且r1,r2,r3∈[1,NP]，F是缩放因子.

Step 3 交叉. 交叉操作是将变异操作得到的变异向量vi,G+1和当前目标向量xi,G按一定规则进行杂交得到实验向量ui,G+1，交叉操作过程如式(6)：

uij,G+1=

(6)

其中i=1, 2, …,NP，j=1, 2,…,D，randb(j)是(0, 1)之间均匀分布的随机数，rnbr(i)是[1,D] 之间随机选择的整数序列，CR是交叉因数.

Step 4 选择. DE算法根据贪婪准则决定实验向量ui,G+1是否成为下一代个体成员. 对实验向量和相应目标向量进行目标函数评价，然后根据式(7)决定是否将实验向量确定为下一代种群个体成员.

(7)

其中f(·)表示其目标函数值.

Step 5 边界条件的处理. 在大多数的问题中，必须确保新产生个体位于边界约束内.为保证这一点，用在可行域中随机生成的个体向量替代超出边界约束的新个体.

3 仿真实验与结果

3.1 创建仿真模型

由于人体头部近似球体，对二维EIT研究，可采用同心圆模型进行仿真实验研究 本文在ANSYS10.0软件上采用有限元法对头部进行二维建模，其三层同心圆模型如图1(a)，该模型由430个三角形单元和901个节点组成.模型由头皮、颅骨、大脑、病变组织四个部分[10]组成. 为简化计算，将该二维模型看成各向同性均质导体，且电阻率值已知. 在仿真试验中，将四个部分的电阻率值设置为：头皮∶颅骨∶大脑∶病变组织=1∶15∶1∶2[11]. 其目标电阻率分布如图1(b)，其中浅色区域为病变组织.

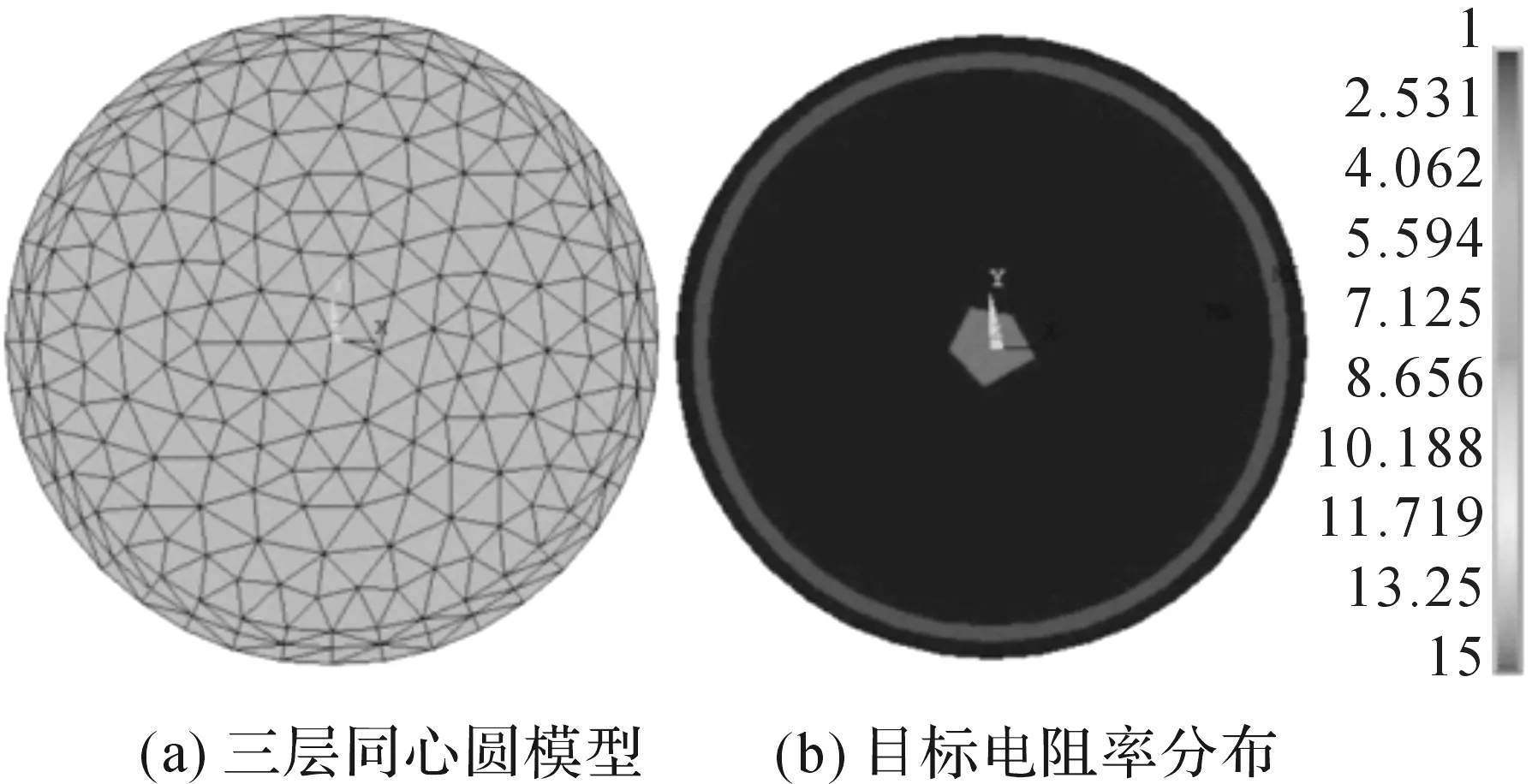
图1 仿真模型Figure 1 Simulation model

3.2 仿真实验条件

本文采用图1(a)所示的三层同心圆模型进行仿真实验，采用相对电极注入方式在模型的左右两侧注入±5 mA的电流. 在图像逆问题重构实验中，将此模型各个部分电阻率比值的上下限分别设为[1.20, 17.40, 1.20, 2.25]，[0.81, 13.60, 0.81, 1.75]. 由于大脑和头皮部分的电阻率比值相等，为简化计算，将DE算法的变量个数设定为D= 3,目标函数为式(4)，算法终止条件为：最大迭代次数为130或个体目标函数值f(ρ)小于10-6，如果在算法终止前没有搜索到近似最优解则认为搜索失败.

为了对算法图像重构质量进行定量分析，引入误差总和TE准则，定义如下：

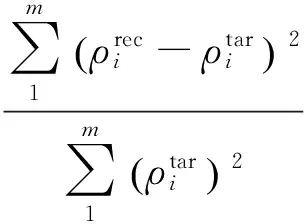
(8)

其中，m为电阻率分布自由度，ρitar和ρirec分别代表单元i的目标电阻率值和重构电阻率值.

为确定DE基本策略DE/rand/1/bin中各个参数对图像重构的影响，对三个参数值的选取进行了仿真试验. 种群大小NP设置为10到60，步长为5；缩放因子范围F为0.1到1.5，步长0.1；交叉因数CR范围为0.1到1.0，步长为0.1. 与其他进化算法类似，DE是通过随机搜索来获得最优解的，每次DE的输出都是不确定的. 因此需要进行多次重复试验以获得平均输出结果.

为确定参数组合的重复试验次数，随机选择6组参数组合进行300次重复试验，计算前n(n为1 ～ 300之间的整数)次误差总和和求解目标函数次数的平均值. 其结果如图2、3，其中，用 (x1,x2,x3) 代表参数NP、F、CR的值分别为x1、x2、x3时的一组参数组合，求解目标函数次数nf=NP× (g+1 )，g为算法收敛代数.

图2 平均误差总和随运行次数变化曲线Figure 2 Change of average total error with run times

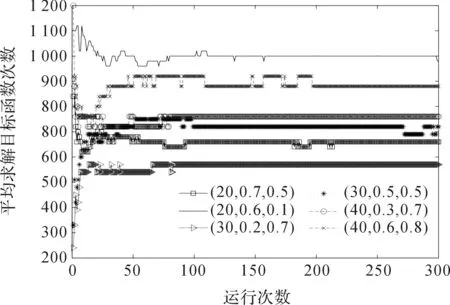
图3 平均求解目标函数次数随运行次数变化曲线Figure 3 Change of average number of objective function solved with run times

从图2、3中可看出，当每组参数组合的运行次数在120以下时，平均误差总和和平均求解目标函数次数曲线变动较为剧烈，而运行120次以上时，其曲线基本上为一条直线，说明当实验次数达到120以后，增加实验次数，基本上不能提高图像重建算法的性能. 因此，在以下的试验中，将每组参数组合的重复实验次数设置为120，取其搜索成功率，并计算在搜索成功情况下求解目标函数次数以及误差总和的平均值.

3.3 种群规模对重构结果的影响

从算法的复杂度来看，种群规模NP越大，算法搜索范围越大，得到全局最优解的可能性越大，但所需的计算时间也越长. 因此种群规模的合理选取对提高算法的搜索效率具有重要的作用. 为确定NP对图像重构的影响，在三组F与CR的值分别设定为0.3、0.7，0.5、0.5，0.8、0.3的情况下，将NP由5增加到60，步长为5. 其重构结果如图4～6.

图4 搜索成功率随种群规模变化曲线Figure 4 Change of search success rate with population size

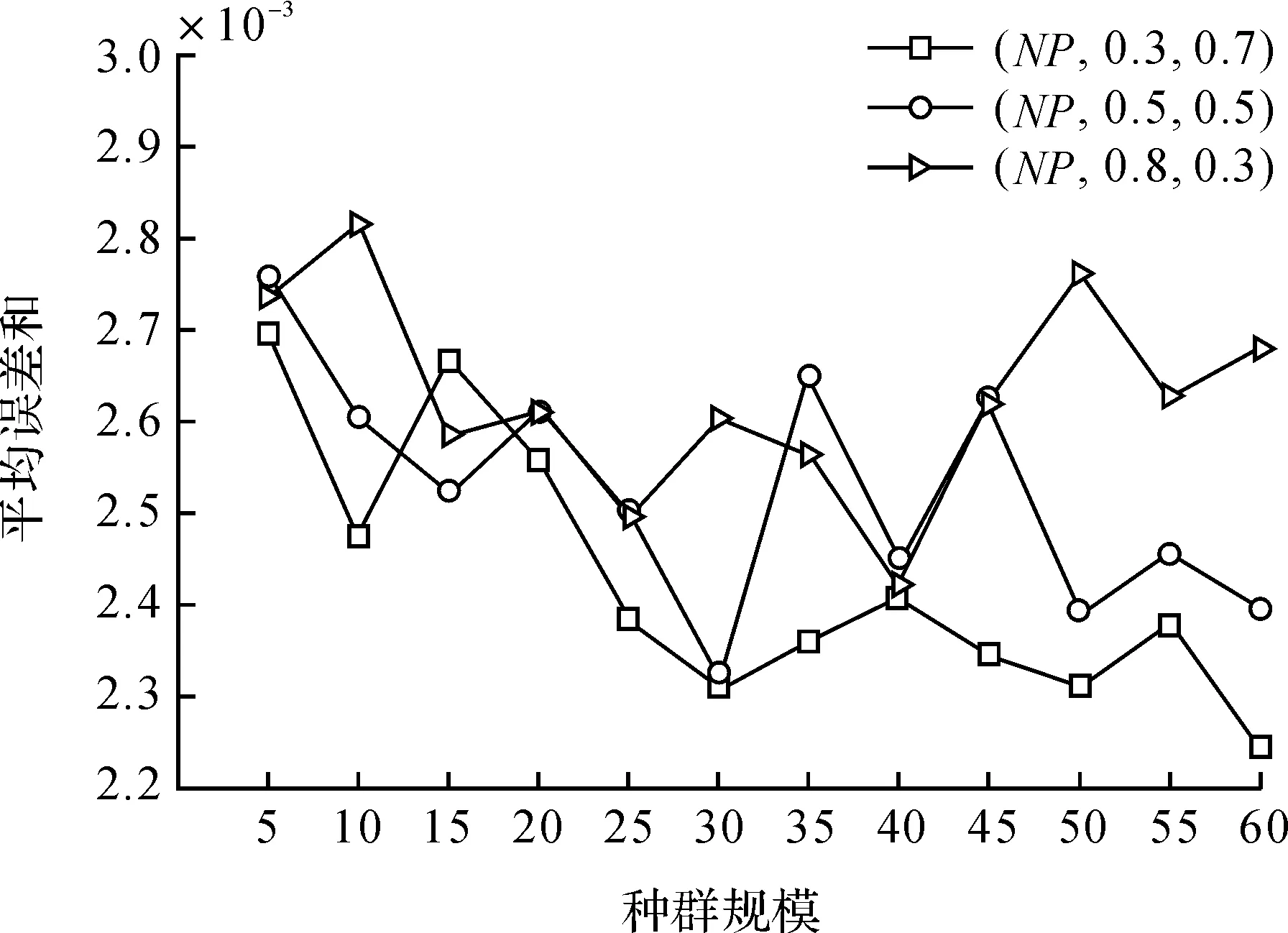
图5 平均误差总和随种群规模变化曲线Figure 5 Change of average total error with population size

图6 平均求解目标函数次数随种群规模变化曲线Figure 6 Change of average number of objective function solved with population size

由图4可知，随着NP的增大，算法搜索成功率越来越高.NP小于10时，算法的搜索成功率都小于80%，而当NP在25以上时，算法的搜索成功率都达到了100%. 由图5可知，NP增大时，误差总和呈无规律波动，但所有平均误差总和都处于2.5×10-3～ 2.8×10-3之间，解的精度基本不变. 但从图6可看出，随着NP的增大，平均求解目标函数的次数不断增大，收敛速度越来越慢. 因此，在给定最大迭代次数的情况下，NP在10 ～ 40之间时，在保证搜索成功率和图像重构精度的情况下，算法能够获得较高的搜索效率，性能较好.

3.4 缩放因子对重构结果的影响

由式(4)可知，在一定程度上缩放因子F决定了种群进化的方向，对算法的局部搜索及全局搜索能力起到一定的调节作用.F较小时，种群多样性较低，但能够提高算法局部搜索能力同时加快算法的收敛；F较大时，有利于提高种群的多样性，算法类似于随机搜索，降低了算法的收敛速度.

为研究F对图像重构结果的影响，在三组NP与CR的值分别设定为20、0.4，30、0.5，40、0.9的情况下，将F由0.1增加到1.5，步长为0.1. 其重构结果如图7～9.

由图7可知，当F< 0.4时，在一定的迭代次数下，算法找到最优解概率低于100%，但随着F的增大，其搜索成功率逐渐增大. 当F≥ 0.4时，其搜索成功率达到100%. 从图8可知，随着F的改变，平均误差总和呈无规则变化，但都处于2.2×10-3～ 3.0×10-3之间，解的精度变化不大. 但从图9可看出，当F≥ 0.4时，随着F的增大，虽然解的精度不一定降低，其求解目标函数次数不断增大，算法收敛速度逐渐减慢. 因此，在一定的迭代次数下，为确保算法在种群多样性和收敛速度上取得良好的平衡，将F的初始合适区间取为0.4 ～ 1.0.

图7 搜索成功率随缩放因子变化曲线Figure 7 Change of search success rate with scaling factor

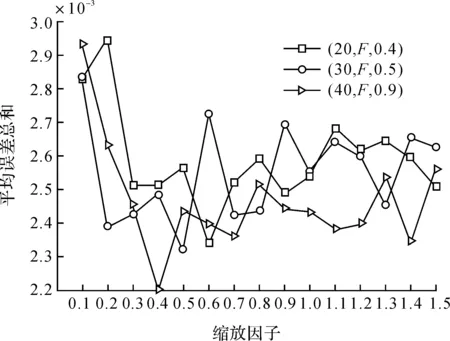
图8 平均误差总和随缩放因子变化曲线Figure 8 Change of average total error with scaling factor

图9 平均求解目标函数次数随缩放因子变化曲线Figure 9 Change of average number of objective function solved with scaling factor

3.5 交叉因数对重构结果的影响

对交叉因数CR对重构结果的试验中，按照类似的方法，先固定NP和F，然后将CR的值从0.1增加到1.0，步长为0.1. 其部分实验结果如图10、11，其中所有参数组合设置的搜索成功率均为100%.

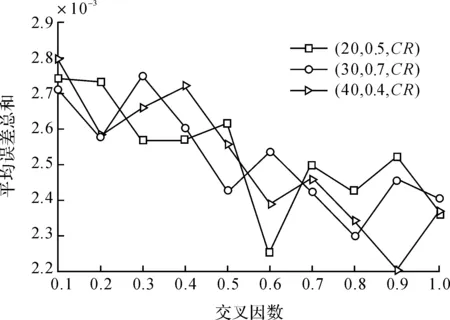
图10 平均误差总和随交叉因数变化曲线Figure 10 Change of average total error with crossover factor

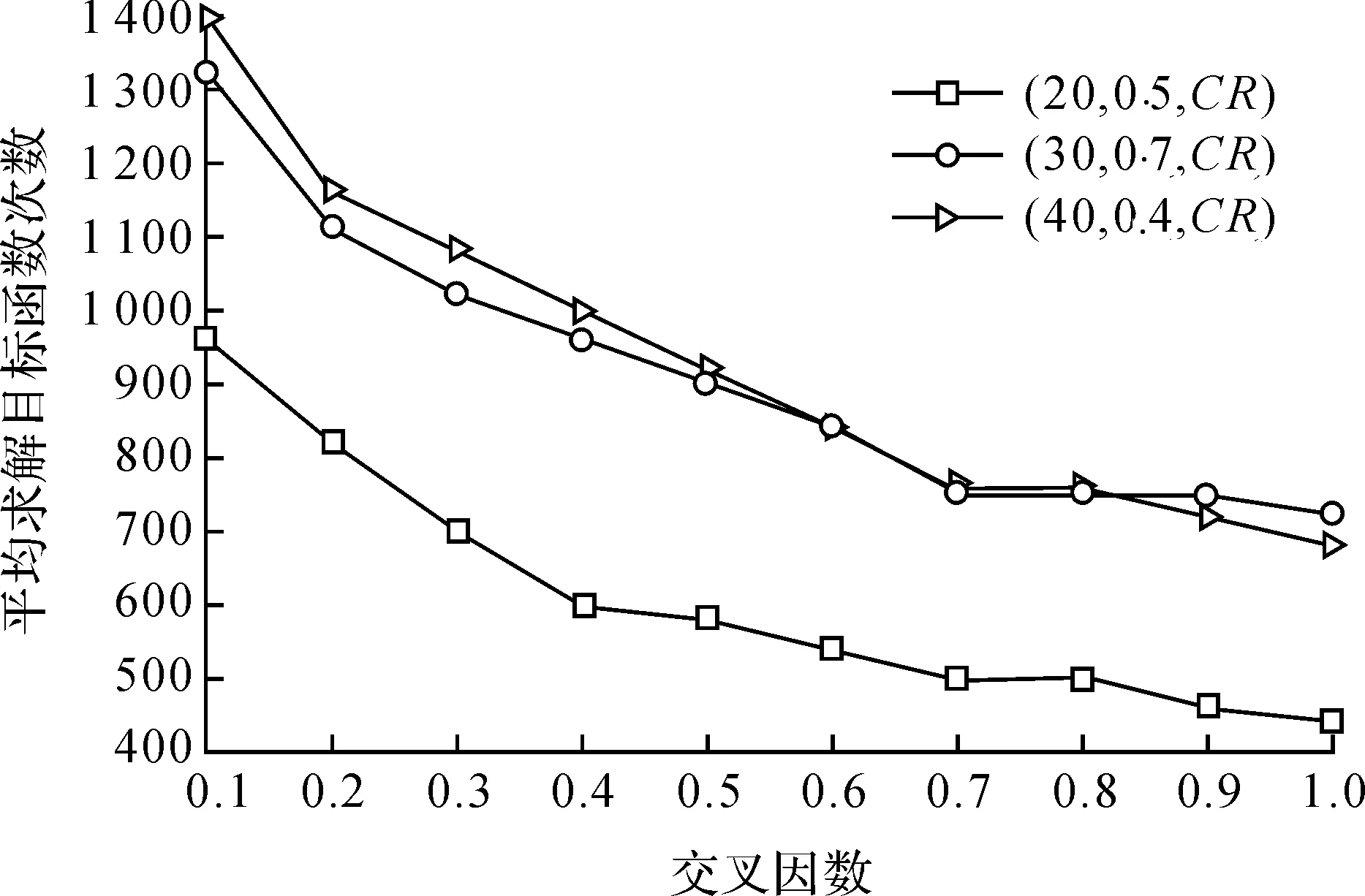
图11 平均求解目标函数次数随交叉因数变化曲线Figure 11 Change of average number of objective function solved with crossover factor

从图10、11可看出，随着CR的增大，整体的误差总和呈现下降的趋势，且平均求解目标函数次数不断下降. 说明CR较小时，种群进化能力降低，收敛速度慢、所需计算时间较长；而CR较大时，种群多样性增强，收敛速度快、所需计算时间短. 因此，为提高图像重构效率和精度，将CR取值设定在0.4 ～ 1.0区间上.

4 结 论

DE算法是一种易于种群进化的启发式算法，逐渐应用于EIT图像重建中. 本实验在二维同心圆模型上采用DE算法的基本策略DE/rand/1/bin对头部电阻率进行重构实验，在给定目标函数和终止条件的基础上，对影响重建质量和效率的三个主要控制参数进行了详细的分析与研究，并给出了电阻抗重构中DE算法控制参数合理选取范围. 结果表明，基于DE算法的EIT重构算法的性能对参数的选择非常敏感. 而NP、F、CR分别设定在10～40、0.4～1.0、0.4～1.0区间上时，在保证搜索成功率的前提下，图像重构精度和重构效率较高.

本文工作为EIT图像重构中DE算法控制参数的选取提供了可靠的定量分析数据，对EIT图像重构中DE算法的改进与参数优化具有一定的指导意义. 下一步将对参数间的相互影响以及三维EIT图像重构中的参数选取问题展开研究. 此外在本文的基础上，对DE算法的改进还有许多问题亟需解决.

[1] SILVERA-TAWIL D, RYE D, SOLEIMANI M, et al. Electrical impedance tomography for artificial sensitive robotic skin: a review[J].IEEESensorsJournal, 2015, 15(4): 2001-2016.

[2] FEITOSA A R S, RIBEIRO R R, BARBOSA V A F, et al. Reconstruction of electrical impedance tomography images using particle swarm optimization, genetic algorithms and non-blind search[C]//BiosignalsandBioroboticsConference. Salvador: IEEE, 2014:1-6.

[3] WAGENAAR J, ADLER A. Electrical impedance tomography in 3D using two electrode planes: Characterization and evaluation[J].PhysiologicalMeasurement, 2016, 37(6): 922-937.

[4] SCHULLCKE B, GONG B, MOELLER K. Steps towards 3D Electrical Impedance Tomography[C]//InternationalConferenceoftheIEEEEngineeringinMedicineandBiologySociety. Milan: IEEE, 2015: 5323-5326.

[5] MARTIN S, CHOI C T M. Nonlinear electrical impedance tomography reconstruction using artificial neural networks and particle swarm optimization[J].IEEETransactionsonMagnetics, 2016, 52(3): 1-4.

[6] FAN Q, YAN X. Self-adaptive differential evolution algorithm with discrete mutation control parameters[J].ExpertSystemswithApplications, 2015, 42 (3): 1551-1572.

[7] YIT K K, PARVATHY R. Differential-evolution control parameter optimization for unmanned aerial vehicle path planning[J].PlosOne, 2016, 11(3): 1-12.

[8] LEON M, XIONG N. Adapting differential evolution algorithms for continuous optimization via greedy adjustment of control parameters[J].JournalofArtificialIntelligence&SoftComputingResearch, 2016, 6(2): 103-118.

[10] HAMILTON S J, LASSAS M, SILTA-NEN S. A direct reconstruction method for anisotropic electrical impedance tomography[J].InverseProblems, 2014, 30(7): 1375-1378.

[11] 闫丹丹, 陈会. 基于电阻抗成像技术的脑病变组织检测仿真研究[J]. 中国医学影像技术, 2014, 30(7): 1113-1116. YAN D D, CHEN H. Detection of brain anomaly based on electrical impedance imaging simulation research [J].ChineseJournalofMedicalImagingTechnology, 2014, 30(7): 1113-1116.

algorithmbasedondifferentialevolution

LIU Hai, YAN Dandan, JING Huimin

(College of Information Engineering, China Jiliang University, Hangzhou 310018, China)

2096-2835(2017)03-0345-07

10.3969/j.issn.2096-2835.2017.03.013

2017-06-15 《中国计量大学学报》网址zgjl.cbpt.cnki.net

国家自然科学基金资助项目(No.51107130).

TP39；R3

A