水基铜纳米流体管内颗粒凝并的数值模拟研究

华轶聪，尹招琴，凃程旭，包福兵

(中国计量大学 计量测试工程学院，浙江 杭州310018)

水基铜纳米流体管内颗粒凝并的数值模拟研究

华轶聪，尹招琴，凃程旭，包福兵

(中国计量大学 计量测试工程学院，浙江 杭州310018)

采用大涡模型和泰勒展开矩方法对三维水平圆管中水基铜纳米流体的运动和颗粒扩散及凝并过程进行了数值模拟,主要研究了纳米流体中纳米颗粒在管内的演化过程.结果显示,随着颗粒凝并的进行, 颗粒粒径增加，数密度减小；小颗粒的混合和颗粒凝并同时改变颗粒粒径，最终使粒径在径向呈现抛物线分布；流场雷诺数越大对凝并的抑制作用越强.

纳米颗粒; 布朗凝并; 泰勒展开矩方法;数值模拟

Abstract: In this paper, the motion, particle diffusion and coagulation of the Cu/water nanofluid in 3D horizontal circular tube are simulated by using the LES model and the Taylor expansion moment method. The evolution of nanoparticles in the tube was studied. The results show that the particle size increases and the density decreases with the particle coagulation. The mixing of the small particles, the particle coagulation and the particle size are changed at the same time, which leads to the distribution of the parabola in the radial direction. The larger the flow field Reynolds number is, the stronger the inhibition of coagulation.

Keywords: nanoparticle; Bowian coagulation; Taylor expansion moment method; numerical simulation

纳米流体作为一种新型高效换热工质展现出良好的换热性能，引起了许多研究者的关注.纳米流体的换热性能相比基液一般可提高至1.05～1.28倍[1].但是，纳米颗粒在流场中运动存在团聚现象.颗粒的聚集改变了纳米流体的均匀性，进而改变其物性参数，对流动和换热过程有重要影响.所以，需要明确纳米颗粒在流场中的团聚现象及运动规律，探索非均匀纳米流体的流动[2-7].

目前微纳米级颗粒在圆管中输运与凝并的研究相继展开.王文龙[8]等在对圆环腔内纳米流体的研究中发现在自然对流过程中纳米流体浓度会抑制换热性能.Ding和Wen[9]研究了稀相层流压力驱动圆管颗粒的迁移，发现壁面附近区域的颗粒浓度远低于中心区域的浓度.林建忠[10]等人研究了圆管中纳米颗粒的凝并并发现纳米颗粒在圆管中的运动和分布特性与微米颗粒是不同的，并对其分布特征进行了详细的介绍.Peng[11]等对纳米颗粒在光滑的水平圆管中压降的变化做了研究，发现压降随着颗粒的质量分数增大而增大.Lam Y C[12]等人对圆管中微米级浓相颗粒的运动做了研究，发现运动过程中径向颗粒数密度最高位置既不在中心位置也不在壁面位置，最高数密度位置在r/R=0.8～0.9(靠近中心位置)；颗粒数密度在壁面上是最低的，并且先随着和壁面之间距离的增大而增大直至最大位置；之后数密度逐渐减小至中心位置.根据以往研究发现，关于湍流状态下管内浓相纳米流体凝并的研究偏少，该方面具有理论和实际意义的研究结果很少.

在欧拉方法的框架内，基于Smoluchowski平均场理论的颗粒通用动力学方程揭示了纳米颗粒两相流中纳米颗粒动力学特征参数演化规律[2].本文采用矩方法对该方程进行数值求解.矩方法可以在保证高精度的情况下，具有较高的计算效率，故其被广泛应用于纳米颗粒的机理研究以及实际工业过程中纳米颗粒的演变过程的预测.但是，由矩方法得到的矩方程，存在难以封闭以及需要重构等问题[13].本文使用泰勒展开距方法解决此问题.泰勒展开距方法是指用泰勒展开技术解决矩方程的封闭问题[14].该方法无需对颗粒尺度分布函数进行预先假设，需要求解的矩方程的个数与泰勒级数展开的阶数相等.

应用泰勒展开矩方法方面，张晓彤[15]对滑移区纳米颗粒输运方程提出了改进的泰勒展开距方法，并对其求解精度及相关应用作了说明.徐飞彬等人[16]对二维方腔热对流中的纳米颗粒凝并特征做了相关研究.发现在非均匀流动系统中，纳米颗粒群演化分为三个阶段：扩散阶段,混合阶段,充分混合阶段，且颗粒群分布最后达到自相似分布.刘淞[17]运用泰勒展开距方法对二维射流做了数值仿真.总的来说，关于液体基纳米流体流动过程中颗粒凝并研究较少.故本文重点对水基铜纳米流体管内湍流状态下颗粒的扩散和凝并过程进行研究.

1 数学模型

1.1 流场计算模型

本文用大涡模拟方法对流场进行模拟，其基本思路是对流场大尺度涡通过直接求解Navier-Stokes方法得到，小尺度涡则通过亚格子模式进行模拟.

连续性方程：

(1)

动量方程：

(2)

能量守恒方程：

(3)

(4)

本文采用Smargorinsky涡黏模式作为亚格子模式.假定用各向同性滤波器过滤器过滤掉的小尺度脉动是局部平衡的，即由可解尺度向不可解尺度的能量传输等于湍动能的耗散率，则可以采用涡黏性形式的亚格子Reynolds应力模式

(5)

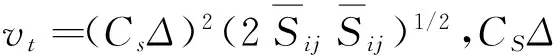
(6)

1.2 颗粒运动方程

本文的仿真是基于流场为非定常、不可压缩、充分发展的湍流.仿真的基液选取的是水，纳米颗粒为铜纳米颗粒.将颗粒单位体积的颗粒个数(数密度)表示成关于空间位置、颗粒体积和时间的连续函数n=n(x,v,t)，即颗粒数密度的通用动力学方程可以表示为

(7)

其中，DC为颗粒的扩散系数，表达式如下：

(8)

式(8)中，B为迁移率；f为颗粒所受阻力的摩擦系数.CC为修正系数，其表达式为

CC=1+Kn[1.142+0.558exp(-0.999/Kn)].

式(7)中的其他变量的物理含义分别是：u为流场的速度.颗粒的凝并项则表示颗粒的凝并，其表达式可以写为

n(v2,t)dv2.

(9)

则式(8)表示为以下方程：

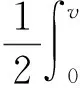
其中β为颗粒的碰撞系数，其表达式为：

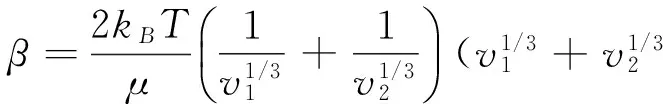
针对式(10)，本文采用泰勒展开矩方法求解处理.首先对i阶矩做定义即：

(12)

式中，i为矩的阶数.在给定位置和时间、每单位体积中为v到v+dv颗粒的数量为dN=n(v,t)dv，含体积v到v+dv颗粒的体积为dV=vn(v,t)dv.因此，零阶矩为

(13)

其表示的是颗粒的总数目.一阶矩为

(14)

其表示颗粒的总体积，在确定颗粒相对密度的情况下，颗粒的同体积与颗粒总质量成正比.

根据对数正态分布假设，可以求得各阶矩分布偏差的数学表达式为

(15)

为了方便对用矩方法求解的结果进行比较，对表达式进行无量纲处理:

Mi=miMi0,

(16)

(17)

(18)

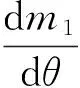
(19)

(20)

其中,θ=B2Nt.B2=3kBT/2μ，在T=353K，kB=1.38×10-23，μ=0.000 356 Pa·s的情况下，B2=2.052 556×10-17.另外本文的颗粒碰撞频率函数的系数

.

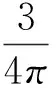
(21)

2 研究结果与讨论

2.1 计算模型与参数

计算模型如图1，本文仿真的几何模型为三维水平直圆管，包含纳米颗粒的流体自左向右流动.管道直径D为40 mm，半径为R，r为径向位置的距离，管道L全长1 000 mm.

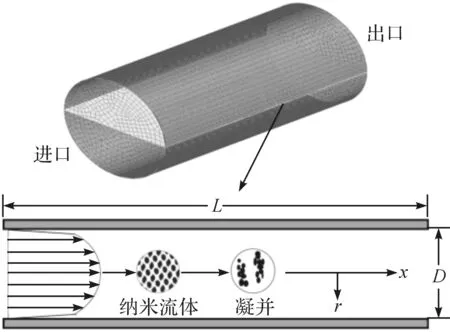
图1 几何模型与坐标系示意图Figure 1 Geometric model and coordinate schematic diagram

本文仿真的对象是铜纳米颗粒以及流体水，计算时流体的温度设定为353 K，动力粘度为3.56×10-4Pa·s，密度为971.83 kg/m3.纳米颗粒方面，其密度为8 930 kg/m3、玻尔兹曼常数kB=1.38×10-23J/K.进口速度采用抛物线入口.

2.2 纳米颗粒凝并结果分析

图2和图4分别为dp0=1 nm,Re=4367和dp0=1 nm,Re=34 942，12.5D处不同时间的粒径在径向分布曲线.如图所示，管道内的纳米颗粒从流体流动开始就产生了碰撞凝并(无量纲平均粒径值大于1)，根据凝并随时间演化过程，可将该过程分为两个阶段即扩散阶段、混合阶段[15].

不同雷诺数下，扩散阶段维持的时间不同.在图2工况下，当t<10 s时处于扩散阶段；而在图4工况下，当t<1 s时处于扩散阶段.在扩散阶段可以发现，颗粒平均粒径参考值在壁面附近位置最小并随着与壁面位置距离的增大而增大，直至达到中心位置附近的最大值.产生此种分布的原因在于，流动伊始来流中心位置附近的速度更大而将更多颗粒带到参考位置中心界面附近，产生更多碰撞凝并.

为明确颗粒凝并与流动状态之间的关系，引入湍流粘度μt.湍流黏度是当流体流动处于湍流状态时，由于随机脉动造成的强烈涡团扩散和级联散列，就像流体具有很大的粘性，具有粘性的量纲.其表达式为

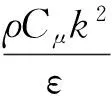
(21)

其中Cμ为经验系数，通常取0.09，k为湍动能，ε为团动能耗散率.

图2 dp0=1 nm，Re=4 367，12.5D处粒径分布图Figure 2 Particle size distribution map on 12.5D, dp0=1 nm,Re=4 367

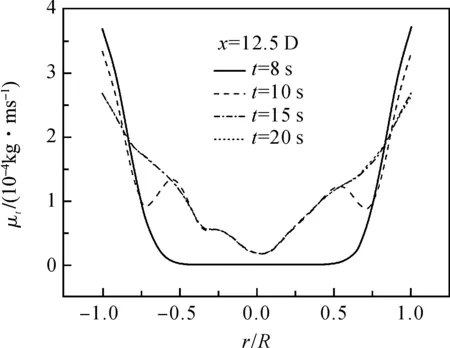
图3 dp0=1 nm，Re=4 367，12.5D处湍流黏度分布图Figure 3 Turbulent viscosity distribution map on 12.5D,dp0=1 nm,Re=4 367

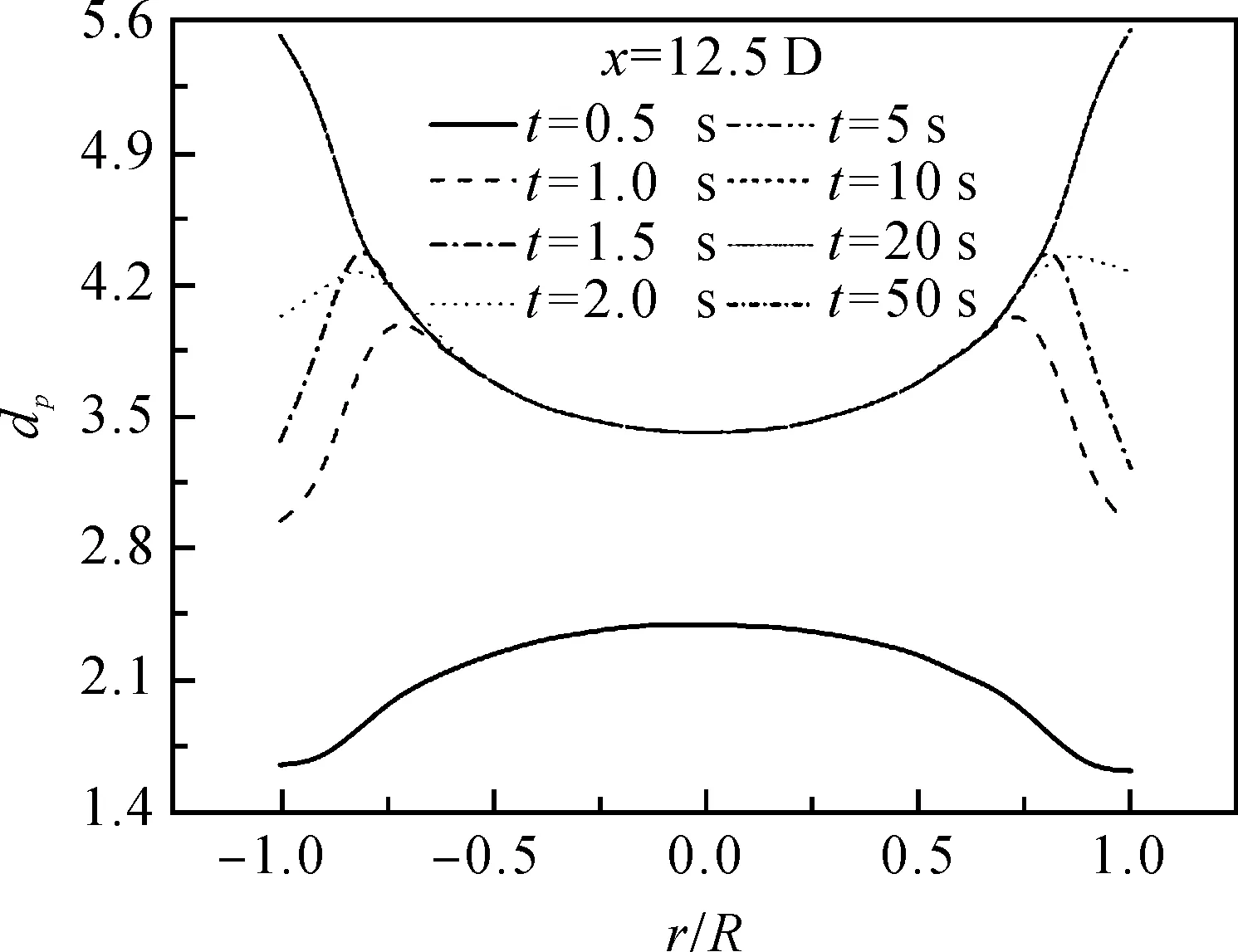
图4 dp0=1 nm，Re=34 942，12.5D处粒径分布图Figure 4 Particle size distribution map on 12.5D, dp0=1 nm,Re=34 942

图3和图5分别为dp0=1 nm,Re=4367和dp0=1 nm,Re=34 942，12.5D处不同时间的湍流黏度在径向分布曲线.由图可知，此阶段中心位置附近湍动粘度非常小而壁面位置附近相对较大.湍动粘度大，说明湍动能大，耗散慢；也就意味着湍流强度相应大，对应位置的速度梯度也大.所以，剪切作用对壁面附近位置的颗粒作用更强，导致凝并作用减弱，最终形成了图2的粒径尺度分布曲线.

从混合阶段开始，管道中心位置的粒径随时间增加幅度较微小.相反，靠近壁面位置的颗粒粒径随时间渐渐变大最终超过中心位置附近的平均粒径.产生此现象的原因是一方面纳米流体持续流入管道，中心来流速度大，将新的颗粒更快地带到管道的中心，同时产生新的碰撞凝并，由于新颗粒的粒径相对偏小，故凝并后使平均粒径反而比壁面附近颗粒平均粒径小.而此时壁面附近来流速度小，该区域流入新的小颗粒较少，且随着原来颗粒凝并过程进行，粒径持续增长.最终靠近壁面颗粒的平均粒径比中心要大.图3和图5还显示，从壁面到r/R=±0.7位置的湍动粘度在此阶段逐渐减小，剪切作用逐渐减小，有利于该位置颗粒凝并.

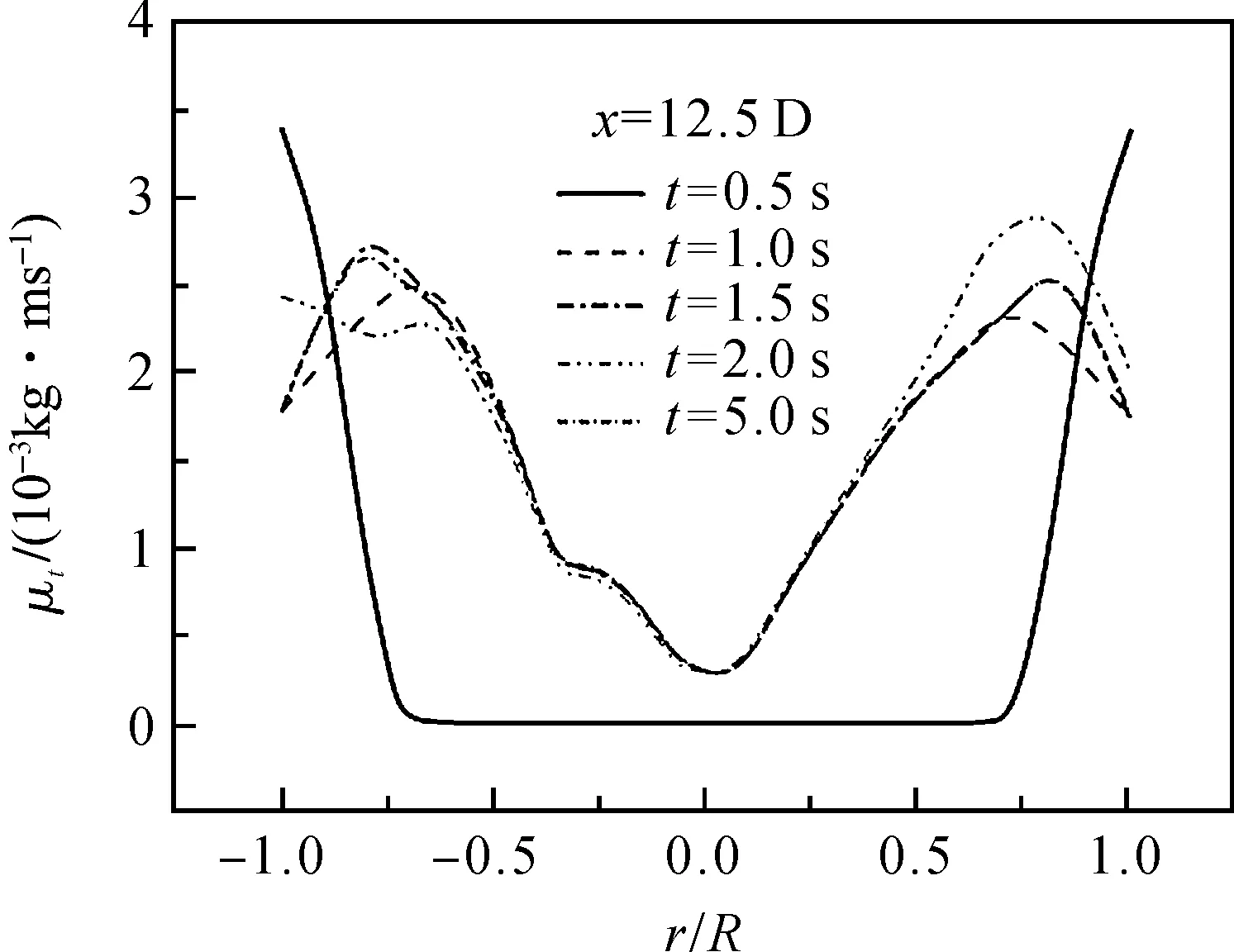
图5 dp0=1 nm，Re=34 942，12.5D处湍流黏度分布图Figure 5 Turbulent viscosity distribution map on 12.5D,dp0=1 nm,Re=34 942

图6 dp0=1 nm，Re=34 942，z=0截面数密度分布图Figure 6 Density distribution map on z=0 section, dp0=1 nm,Re=34 942

图6为dp0=1 nm，Re=34942，z=0截面数密度分布云图.由图可知中心位置附近数密度大，越贴近壁面数密度越小.颗粒因为凝并使数密度减小，同时又因为新颗粒的流入，增加了颗粒的数密度.图6显示的颗粒数密度分布和图2、图4显示的颗粒粒径分布彼此对应，表达了颗粒凝并和扩散过程对于颗粒数密度和粒径影响的共同作用结果.

根据各工况的粒径演变图可知，入口雷诺数越大，工况达到混合阶段所需要的时间就越少.这是由于雷诺数越大，入口平均速度就越大，来流会更快将小粒径纳米颗粒带到参考位置产生碰撞凝并.高雷诺数(图5)的湍动粘度明显大更低雷诺数(图3)湍动粘度一个量级(10倍)左右.这意味着高雷诺数会带来更强的剪切效应.比较图2(Re=4 367)和图4(Re=34 942)，发现小颗粒的混合和高剪切效应的抑制最终导致高雷诺数下颗粒平均粒径小于低雷诺数下粒径值.说明高雷诺数对颗粒凝并具有抑制作用.最终，由图2和图4可知，每个工况粒径随时间变化曲线都是相似的，粒径大小在径向为抛物线型分布.

3 结 论

纳米颗粒在水中的凝并研究在强化传热过程中具有重要的物理量意义.本文结合大涡模拟和泰勒展开矩方法对水平直圆管内的纳米颗粒群凝并特征进行了详细的数值模拟.根据纳米颗粒数密度和粒径演化图，得出以下结论：

1)纳米颗粒在基液中会产生凝并现象，凝并使颗粒粒径增加，数密度减小；

2)纳米颗粒在流动过程中发生扩散和混合，小颗粒的混合和颗粒凝并同时改变颗粒粒径，最终使粒径在径向呈现抛物线分布；

3)湍流黏度对凝并起抑制作用，流动雷诺数增加，颗粒粒径增长缓慢.

[1] 王彩霞,黄云, 姚华, 等.纳米流体研究进展[J].储能科学与技术, 2017, 6(1): 24-34. WANG C X, HUANG Y, YAO H. The research progress of nanofluids[J].EnergyStorageScienceandTechnology, 2017, 6(1): 24-34.

[2] 林建忠,于明州,林培峰,等.纳米颗粒两相流体动力学[M].北京：科学出版社, 2013：77-79,221-222.

[3] LIN J, LIN P, CHEN H. Research on the transport and deposition of nanoparticles in a rotating curved pipe[J].Physicsoffluids, 2009, 21(12):1-11.

[4] YU M Z, LIN J Z. Taylor-expansion moment method for agglomerate coagulation due to Brownian motion in the entire size regime[J].JournalofAerosolScience, 2009, 40(6): 549-562.

[5] YU M Z, LIN J Z, CHAN T L. Numerical simulation of nanoparticle synthesis in diffusion flame reactor[J].PowderTechnology, 2008, 181(1): 9-20.

[6] YU M Z, LIN J Z, CHAN T L. Effect of precursor loading on non-spherical TiO2nanoparticle synthesis in a diffusion flame reactor[J].ChemicalEngineeringScience, 2008, 63(9): 2317-2329.

[7] YIN Z Q, LIN J Z, ZHOU K, et al. Numerical simulation of the formation of pollutant nanoparticles in the exhaust twin-jet plume of a moving car[J].InternationalJournalofNonlinearSciencesandNumericalSimulation, 2007, 8(4): 535-544.

[8] 王文龙,徐旭,王宇飞,等.圆环腔内纳米流体自然对流的数值研究[J].中国计量学院学报,2013,24 (1):19-24. WANG W L, XU X, WANG Y F, et al. Numerical study of the natural convection of nanofluid in a ring cavity[J].JournalofChinaUniversityofMetrology,2013,24 (1):19-24.

[9] DING Y, WEN D. Particle migration in a flow of nanoparticle suspensions[J].PowderTechnology, 2005, 149(2): 84-92.

[10] LIN J Z, LIU S, TATLEUNG C. Nanoparticle migration in a fully developed turbulent pipe flow considering the particle coagulation[J].ChineseJournalofChemicalEngineering, 2012, 20(4): 679-685.

[11] PENG H, DING G, JIANG W, et al. Measurement and correlation of frictional pressure drop of refrigerant-based nanofluid flow boiling inside a horizontal smooth tube[J].InternationalJournalofRefrigeration, 2009, 32(7): 1756-1764.

[12] LAM Y C, CHEN X, TAN K W, et al. Numerical investigation of particle migration in poiseuille flow of composite system[J].CompositesScienceandTechnology, 2004, 64(7): 1001-1010.

[13] WRIGHT D L, MCGRAW R, ROSNER D E. Bivariate extension of the quadrature method of moments for modeling simultaneous coagulation and sintering of particle populations[J].JournalofColloidandInterfaceScience, 2001, 236(2): 242-251.

[14] YU M Z, LIN J Z, CHAN T. A new moment method for solving the coagulation equation for particles in Brownian motion[J].AerosolScienceandTechnology, 2008, 42(9): 705-713.

[15] 张晓彤. 泰勒展开矩方法模型的改进及在纳米颗粒两相流中的应用[D].杭州：中国计量大学,2016. ZHANG X T.TheIimprovementofTaylor'sMomentMethodModelandItsApplicationinTwoPhaseFlowofNanoparticles[D]. Hangzhou: China Jiliang University, 2016.

[16] 徐飞彬,周全,卢志明. 二维方腔热对流系统中纳米颗粒混合及凝并特性的数值模拟[J].力学学报, 2015, 47(5): 740-750. XU F B, ZHOU Q, LU Z M. The numerical simulation of the nanoparticle mixing and coagulation character in thermosyphon system of the two-dimensional square cavity[J].ChineseJournalofTheoreticalandAppliedMechanics, 2015, 47(5): 740-750.

[17] 刘淞. 基于三阶矩方法的纳米颗粒凝并与湍流扩散的数值模拟[D].杭州：浙江大学,2008. LIU S.NumericalSimulationofParticleCoagulationandTurbulentDiffusionBasedontheThree-OrderMomentMethod[D].Hangzhou: Zhejiang University, 2008.

[18] 于明州. 纳米粒子多相流矩方法研究[D]. 杭州：浙江大学, 2008. YU M Z.NanoparticlesofCoagulationandDirectNumericalSimulationProcessTwoPhaseTurbulentMomentMethod[D].Hangzhou: Zhejiang University, 2008.

NumericalsimulationofCu/waternanofluidparticlescoagulationinpipes

HUA Yicong, YIN Zhaoqin, TU Chengxu, BAO Fubing

(College of Metrology and Measurement Engineering, China Jiliang University, Hangzhou 310018, China)

2096-2835(2017)03-0300-06

10.3969/j.issn.2096-2835.2017.03.006

2017-07-08 《中国计量大学学报》网址zgjl.cbpt.cnki.net

国家自然科学基金资助项目(No.11402259),浙江省大学生科技创新活动计划项目(No.2016R409059).

O359

A