也谈数学教学中如何培养创新能力

李丽伟

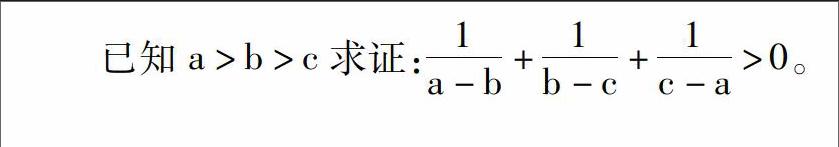
摘要：本文从如下几个方面论述了如何加强学生创新能力的培养，重点论述了创设情景，形成培养创新精神的氛围和重视求异思维、发散思维的培养是增强创新能力的重要渠道两个方面。

关键词：创新；问题；启发

中图分类号：G633.6 文献标识码：B 文章编号：1672-1578（2017）09-0175-02

创新是一个民族的灵魂，是一个国家兴旺发达的不竭动力，没有科学的创新，总是步人后尘，经济就只能受制于人，更不能缩短差距。"因此，在数学教学中必须抓住对学生创新能力的培养。

目前教学现状：虽然在教学模式、内容、方法等方面都作了有益探索，受应试教育的影响，课堂教学中解题数学占据了主导地位，通过大量的练习来学习数学，还是目前数学教学方法的主旋律，大量模仿性练习，对提高基本运算能力，逻辑推演能力以及学生解题能力的确行之有效。但却使得数学教学缺乏创新精神，这说明加强对学生创新能力的培养任务还十分艰巨。

创新一般指，对思维主体来说是别出心裁，突破常规的，首次出现的思维活动，它包括发现新方法、揭示新规律、建立新理论、发明新技术、开发新产品、解决新问题等的思维活动。一个人要有不断创新的精神也就离不开他的创造力。创造力是人通过一定的智力活动，在现有知识和经验的基础上，通过一定的重新组合和独特加工，在头脑中形成新产品的形象，并通过一定的行动使之成为新产品的能力。我们如何在数学教学中加强创新能力的培养呢？

1.重视知识发生的过程，培养创新意识

数学上每一个概念的引入都是由于产生实际需要或是研究某些问题的需要而产生的，一些重要定理的证明往往也体现了一些新的思路新的方法。也就是在当时研究某些问题的需要而有所创新方能突破。因此在教学中重视知识发生过程的教学就是让学生不断感受到随着生产、生活实际的需要，科学研究等方面的需要是会不断出现新问题，要解决这些问题就要求我们在不断总结前人经验的基础上，用于探索，勇于创新。这无疑对于培养学生的创新意识是十分重要的。

2.创设情景，形成培养创新精神的氛围

创新始于"问题"，爱因斯坦强调："发现问题和系统阐述问题肯定要比得到解答更为重要。解答可能仅仅是数学或实验技能问题，而提出新问题、新的可能性，从新的角度去考虑老问题则要求创造性的想象，标志着科学的真正进步。"牛顿发现万有引力始于他在苹果树下的思索："为什么苹果从树上掉下来，而不飞到天上去？"而"问题"来源于好奇心，强烈的好奇心会增强人们对外界信息的敏感性，对新出现的情况和新发生的变化及时作出反映，发现问题并追根溯源、激发思考，引起探索欲望，开始创新活动。许多看似偶然的发现其实都隐含着一种必然：发现者必然有強烈的好奇心理。爱因斯坦有一句名言："我并没有什么特殊的才能，我只不过是喜欢寻根问底地追究问题罢了。"这段话一语道破了创新和发现的真谛：好奇心理、问题意识及锲而不舍的探求。教学中使学生积极主动的投身于学习中是十分重要的，例：在"均值不等式"的教学中，可设计两个实际应用问题，让学生在探索中发现"均值不等式及推论"设计如下：①某商店在节前进行商品降价酬宾活动，拟分三个降价方案：甲方案是第一次打a折销售，第二次打b折销售，乙方案是第一次打b折销售，第二次打a折销售，丙方案是两次都打a+b2折销售，请问哪一种方案降价最多？②一个有毛病的天平（天平的两臂之长略有差异，其它因素忽略）怎样称物体的重量？有人说只要有左右各称一次，再相加除以二就可以了，你认为如何？学生通过审题、分析，展开小组讨论，对于问题①，大多数学生能归纳为比较ab与（a+b2）2大小的问题，进而用特殊值猜出ab≤（a+b2）2（ 对于②有的同学也可结合物理知识，归纳为a+b与a+b2的大小，由①可得a+b2≥a+b。这样的设计易产生明显的意识倾向和情感共鸣。同时教育学生尊重科学，尊重知识，但又不迷信权威，敢于向权威挑战的心理素质。

3.善于启发引导，鼓励创新热情

心理学研究表明，榜样的示范作用对创新意识的形成的重要性是不容忽视的，心理学家西蒙说"对榜样的模仿，促进了创造性的智慧，从而对创造性产生有利的影响。"在班级集体里，一方面可以向学生介绍一些古今中外创新的例子。如：数学家高斯10岁时就发现了"1+2+3+....+100"这道题的特点，发现了快速计算的方法。典故"司马光砸缸救人"的突破常规的思维方法。另一方面要注意发现班级集体中有创新精神的苗子。例如经常会有学生不完全按照老师规定的书写格式、解题步骤以及解题方法去做。我们不要一概加以否定，仔细分析一下是否有某些合理性，是否有某些标新立异之处。如果发现了闪光点即时发扬鼓励，不仅对受表扬的学生往往会终身难忘。同时对其他同学也起了导向作用，可以增强学生的创造欲，鼓励学生的创新热情。

4.突出数学思想方法是增强学生创新能力的基础

学生创造能力的培养与基础知识，基本技能的掌握是密不可分的。没有扎实的基础理论知识攀登科学高峰，即使有丰富的想象力，有一定的创造能力但缺乏基础知识就会使他要想解决的问题不能圆满解决，甚至半途夭折。因此在加强对学生创新能力培养的同时要处理好与基础知识的关系。在基础知识中对于一些死记硬背、模仿性习题应加以控制，不能对学生进行题海战训练，否则将影响学生的创新思维，而有关的重要数学思想方法应予以加强，这是学生终身受用的思维方法，只有把他掌握住了，学生才能在题海中畅游，对所学的内容运用自如，把所学知识转化为能力，故数学思想方法是继续发展，创造能力的基础应当予以充分重视。

5.重视求异思维，发散思维的培养是增强创新能力的重要渠道

培养学生的观察力和想象力。观察力是人类智力结构的重要组成部分，敏锐的观察力是创新活动的起步器。想象是客观现实在人脑中的反映，丰富的想象力是创新活动的设计师。

因此，教学中应引导学生全方位，多角度的观察问题，同时提供想象材料，诱发学生创造性的想象。例：教学中注意教学生一题多解，公式的正用逆用等等，在这过程中要注重求异思维能力和发散思维能力的培养。求异思维就是不墨守成规，寻求变异，伸展扩引，标新立异的一种思维倾向和思维活动。任何一位科学家的创造能力都可以看成是：创造能力=知识量求异思维能力。发散思维是多角度、多方位思考问题的一种思维活动，显然没有"求异"就不可能"发散"，要"发散"就必须"求异"，而当发散思维发生了质的飞跃时，就达到了求异思维的最高境界标新立异，即创新。因此发散思维和求异思维的培养是增强学生创新意识和创新能力的重要渠道。在教学中教师可有目的的设计一些开放题，让学生对问题多角度分析，培养学生的发散思维能力，再进一步可让学生删改条件，探求结论等，都可以更好地培养学生的求异思维能力。重视开放题的研究，已知a>b>c求证：1a-b+1b-c+1c-a>0。

分析：有同学采用如下方法证明方法，1a-b+1c-a=c-b（a-b）（c-a）>0，因此原不等式成立，但发现似乎结论中的"1b-c"多余了，从这一点出发，引导学生观察、分析、类似的有1a-b+1c-a=c-b（a-b）（c-a）>0，对此，师生可以共同努力将此题设计成开放题①已知a>b>c，且1a-b+1b-c+λc-a>0，求λ的范围；②已知a>b>c，且λa-b+λb-c+1c-a≥0求λ的最小值。

6.转变教育观念是加强创新能力培养的可靠保证

我们已经站在新世纪的门槛之上，更新教育观念，改变陈旧的教学观，是21世纪教师的重任。只有这样才能适应时代的需要。数学教育改革的重点之一就是如何培养学生的创新精神、创新能力，我们必须认识到：数学可以帮助人们更好的认识自然和人类社会，更好的适应日常生活，理解周围世界；数学可以促进人们有条理的思考，有效的进行表达个交流，用数学分析问题和解决问题；同时通过数学实践活动还可以发展学生的主动性，责任感和自信心，培养学生实事求是的态度和勇于探索的创新精神。事实上影响创新能力发展的因素是多方面的，而其中最为重要的是，教师要转变教育观念，增强教改意识，树立新的教育观，把提高素质作为教学的根本任务，才能营造创新环境，培养创新能力。

参考文献：

[1] 李兆兰 《素质教育创新》

[2] 李连方 《中学数学研究》endprint