基于Contourlet变换的K-L变换地震随机噪声自适应衰减方法

刘燕峰,邹少峰,居兴国

(中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)

基于Contourlet变换的K-L变换地震随机噪声自适应衰减方法

刘燕峰,邹少峰,居兴国

(中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)

地震资料中有效反射信号具有丰富的纹理及边缘特性,在Contourlet变换域系数较大并具有相关性,而随机噪声均匀分布于Contourlet变换域且系数较小。考虑K-L变换具有分类特征提取的优势,在Contourlet变换基础上应用K-L变换,采用最大似然估计法和多尺度噪声估计法估算地震记录中有效信号及随机噪声的Contourlet系数方差,并将其应用到K-L变换域能量百分比阈值函数的定义中,自适应地确定用于K-L反变换的特征向量,修改Contourlet变换的系数,再进行Contourlet反变换压制随机噪声。数值模拟及实际地震资料去噪效果表明,基于Contourlet变换的K-L变换去噪方法不仅可以有效地压制地震资料中的随机噪声,提高地震资料信噪比,而且具有较好的保真性。

Contourlet变换;K-L变换;最大似然估计;多尺度噪声估计;随机噪声衰减;自适应

变换域噪声压制是指利用数学变换找出某种基函数来稀疏表达有效信号,使有效信号能量主要分布在少数较大的系数上,而噪声分布在较小的系数上,从而实现信噪分离。如20世纪80年代初发展起来的小波变换域噪声压制方法[1-10],利用“正方形”基函数来逼近信号,虽然容易检测出边缘奇异点,但无法准确表示边缘点间的连续性,且缺乏方向性,不能很好地表达图像中的曲线或面奇异。DO等[11]在小波变换的基础上发展了Contourlet变换,用“长条形”基函数来表达信号,其支撑区间的宽度与长度近似符合平方律,具有优越的非线性逼近能力,在图像增强、图像去噪、模式识别、统计分析等领域得到了广泛应用。彭才等[12]将Contourlet变换应用于随机噪声衰减,采用硬阈值法修改Contourlet系数,反变换重建原信号。张恒磊等[13]采用相关叠加和非线性阈值相结合的方法对Contourlet系数进行修改,以压制随机噪声。王建花等[14]利用同一方向子带内相邻Contourlet系数之间的相关性,对每一个系数计算邻域均方根振幅,定义该系数与邻域均方根振幅比值的平方为邻域相关系数,根据邻域相关系数定义阈值函数自适应地衰减随机噪声。

K-L变换最初应用在遥测多谱资料处理中。HEMON等[15]1978年首次将K-L变换应用到地震资料处理领域,基于随机噪声与有效信号的相干性差异去除随机噪声和相干噪声。其后,傅才芳等[16]应用K-L变换去除地震资料中的随机噪声。杨文采[17]用非线性K-L变换去除海洋地震资料中的随机噪声。张广智等[18]先将地震数据分块并拉平相干同相轴,再利用K-L变换进行随机噪声衰减。LIU[19]先选出面波区域并将面波拉平,再用K-L变换提取面波并从原始信号中减去面波,取得较好的去噪效果。

地震资料经Contourlet变换后,有效反射信号的Contourlet系数较大并具有较强的相关性,随机噪声则均匀分布于变换域,系数较小且相关性弱,对Contourlet系数的处理方式决定了Contourlet变换的去噪效果。本文充分利用有效信号的Contourlet系数在同一方向子带内及不同方向子带之间的相关性和非高斯性,结合K-L变换在分类特征提取上的优势,对Contourlet系数进行K-L变换以进一步分离有效信号和随机噪声。利用最大似然估计法[20-21]和多尺度噪声估计法对有效信号和随机噪声的Contourlet系数进行方差估计,并定义K-L变换域能量百分比阈值函数,自适应地确定K-L反变换的特征向量,修改Contourlet变换的系数,再通过Contourlet反变换压制随机噪声。

1 方法原理

1.1 Contourlet变换

Contourlet变换也可称作小轮廓变换,采用分段光滑的基函数对原始信号进行逼近。Contourlet变换可分为两个独立的步骤:①根据信号的特点,采用拉普拉斯金字塔滤波器[11,22](Laplacian Pyramid,LP)对二维信号进行多尺度分解,以捕获不同尺度上信号的边缘奇异点;②通过方向滤波器组[23-25](directional filter bank,DFB)对LP分解后的每一尺度高频信号进行方向分解,并将同方向上的奇异点连成线,合并为同一系数,即Contourlet系数。

1.1.1 拉普拉斯金字塔分解

拉普拉斯金字塔分解源于影像的高斯金字塔分解,即将平滑滤波与下采样操作结合获得原始图像的近似分量,对此近似分量重复进行平滑滤波与下采样操作,则可得到一系列不同尺度的高斯图像金字塔,相邻两层高斯金字塔图像相减则为拉普拉斯金字塔图像。故拉普拉斯金字塔分解过程如下:

1) 通过低通滤波和下采样操作得到原始信号x的近似分量,也就是原始信号的低频子带信号;

2) 对低频子带信号进行上采样和高通滤波,生成原始信号的预测信号d;

3) 将原始信号x与预测信号d相减,得到原始信号的高频子带信号c。

此后利用每一步分解所产生的低频子带信号,迭代进行LP分解,生成一个低频信号和一系列高频子带信号。分解及重构过程如图1所示,其中,H为(低通)分解滤波器,G为(高通)合成滤波器,M为采样矩阵。拉普拉斯金字塔滤波实现了信号从精细尺度到粗略尺度的逼近。

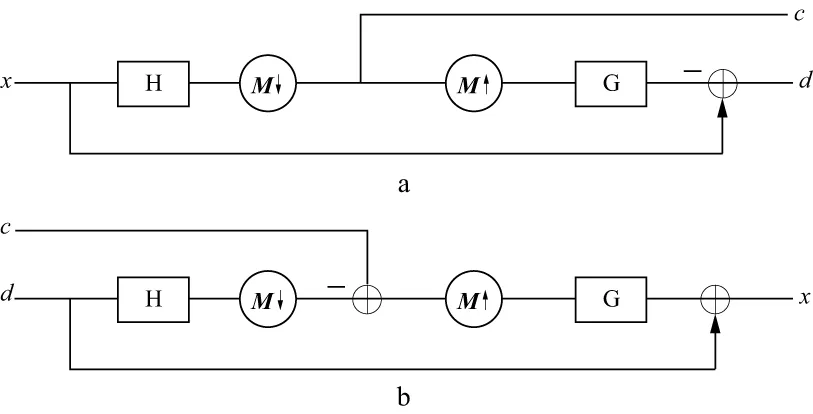
图1 拉普拉斯金字塔分解及重构a 一级分解; b 一级重构

1.1.2 方向滤波器组

方向滤波器组DFB可以通过l级树型分解来实现。在每一级中,频域被划分为2l个楔型的方向子带[25]。DFB的实现分以下两步:①将扇型滤波器与梅花型采样矩阵相结合,实现对原始信号二维频谱的切分,即第一与第二级分解;②从第三级分解开始,将扇型滤波器与幺模采样矩阵相结合,实现局部方向信息的提取。图2为前两级DFB分解的频率分割示意图[16]。第一级和第二级分解采用梅花型采样矩阵Q0,Q1:

(1)

(2)

第三级及以后各步采用幺模采样矩阵,分别为:

DFB的第一级将原始信号经扇形滤波器分解为水平和垂直两个方向(如图2a),第二级将扇形滤波器与梅花型采样矩阵Q0交换形成如图2b所示的象限滤波器,将第一级与第二级滤波器组合后进行Q1采样,则可获得如图2c所示的原始信号4个方向子带。从第三级开始所用的滤波器组是扇形滤波器与幺模采样矩阵形成的平行滤波器组,实现信号的2l级分解。方向滤波器组会将信号的低频分量泄漏于几个方向子带中,在应用之前需要将信号的低频部分移除,因此将LP分解模块与DFB分解模块结合,形成了双层滤波器组结构的Contourlet变换。图3为Contourlet变换基本流程[26],图4为Contourlet变换4级分解系数。

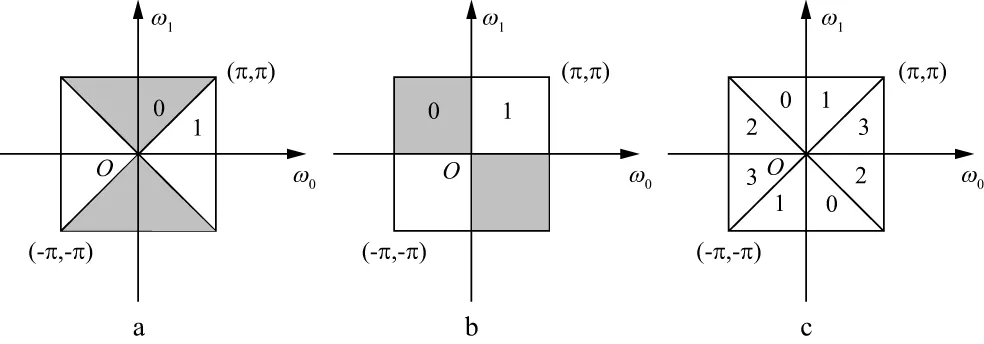
图2 二级方向滤波器组频率分割a 第一级滤波器; b 第二级滤波器; c 第一级与第二级滤波器组合

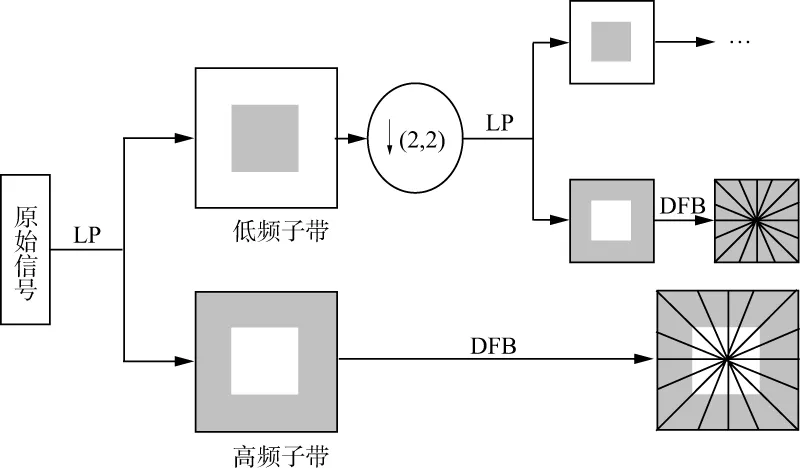
图3 Contourlet变换的基本流程

图4 Contourlet变换4级分解系数

1.2 基于Contourlet变换的K-L变换随机噪声衰减方法

图像经Contourlet变换稀疏表达后,采用边缘统计模型及联合统计模型对变换系数进行研究表明:Contourlet变换系数具有聚类性和持续性,以及非高斯、高峰度和长拖尾等特点[27]。这保证了图像中有效信息主要集中于变换域的有限区域内,且系数较大,而高斯性的随机噪声经Contourlet变换后仍为白噪声,其均匀分布于变换域且幅值较小[28]。同时Contourlet系数之间存在一定的相关性,即如果一个Contourlet系数幅值大,则与其相邻的Contourlet系数很有可能是“大”系数。

地震资料中的有效信号具有丰富的纹理和边缘特征,而随机噪声符合高斯白噪声的特点。有效信号的Contourlet变换域系数较大且相互关联,而随机噪声的Contourlet变换域系数较小且均匀分布于各子带上,无明显相关性。利用这些特性修改Contourlet系数可实现对随机噪声的压制。然而,任何一种变换都不能达到信号与噪声的完全分离,有必要进一步扩大有效信号和随机噪声的分离度。

K-L变换具有分类特征提取的优势,它对输入信号按其协方差矩阵的归一化特征向量进行正交分解。经K-L变换后,存在相干性的有效信号集中在前面几个特征值对应的特征向量上,随机噪声则分布在最后几个特征值对应的特征向量上,反变换时去除代表随机噪声的特征向量,则可将相干性好的有效信号保存下来,压制随机噪声,提高地震资料的信噪比。本文对Contourlet系数进行K-L变换,以最大限度地将有效信号与随机噪声分离。

K-L变换原理[29]如下。

对于第i层第l个方向子带的Contourlet系数矩阵

(7)

其协方差定义为:

(8)

式中:E(C)表示C的数学期望,[C-E(C)]T为[C-E(C)]的转置。Cov(C)为m×m的实对称正定矩阵,存在一个正交矩阵U,使得

(9)

式中:λi是Cov(C)矩阵的特征值;Λ是按照特征值递减顺序排列的对角矩阵;U为特征向量矩阵。

(10)

对二维矩阵C做正交变换可得K-L变换公式:

(11)

式中:UT为U的转置。重构信号公式为:

(12)

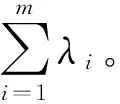
(13)

不同尺度的噪声引起的Contourlet系数方差沿着分解层次近似为指数分布,而同一个尺度内各方向的噪声方差基本相等[30]。因而不同尺度的噪声方差σm可表示为:

(14)

式中:i代表分解层次(尺度);σ1为最小尺度的噪声方差。

σ1可采用经典的鲁棒中值估计法求取[31]:

(15)

式中:cil为第i层、l方向子带系数;median表示求系数中值。

定义第i层、第l个方向子带中大小为m×n,代表有效信号的Contourlet系数方差为σ,利用最大似然估计法来求取[25]:

(16)

在Contourlet域,有效信号与噪声的Contourlet系数是相互独立的,所以输入信号(即含噪信号)的Contourlet系数方差σc满足[32]:

(17)

考虑到实际资料的复杂性,引入调整因子θ∈(0,1),定义K-L变换域能量百分比阈值函数为f(θ),则:

(18)

当p满足:

(19)

时,确定p为用于信号重构的最大特征向量个数。

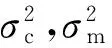
图5为基于Contourlet变换的K-L变换去噪方法流程,具体实现步骤如下:

1) 对输入数据进行Contourlet变换,得到不同尺度、不同方向子带的Contourlet系数矩阵C;

2) 对每个系数矩阵C做K-L变换,得到对应的特征值和特征向量;

3) 利用(14)～(18)式求取K-L变换域能量百分比阈值函数f(θ);

4) 利用公式(19)求取p值,确定K-L反变换时的特征向量个数;

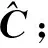
图5 基于Contourlet变换的K-L变换去噪流程

2 数值模拟

对小波变换去噪、常规Contourlet变换阈值去噪和本文基于Contourlet变换的K-L变换去噪方法进行了数值模拟对比试验(图6)。图6a为数值模拟的原始单炮记录;图6b为加入随机噪声的单炮记录,其信噪比为0.55;图6c为小波变换阈值去噪结果,其信噪比为1.02;图6d为Contourlet变换阈值去噪结果,其信噪比为1.28;图6e为本文方法的去噪结果,其信噪比为2.01,优于小波变换阈值去噪结果和Contourlet变换阈值去噪结果;图6f为本文方法去除的噪声。图7为本文方法去噪后单炮记录频谱分析结果,去噪后单炮记录频谱与原始模拟单炮记录频谱相似。说明本文方法不仅对随机噪声有良好的压制作用,而且对有效信号有很高的保真度。

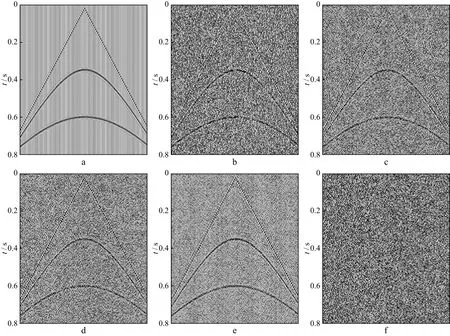
图6 基于Contourlet变换的K-L变换去噪方法处理模型效果分析a 原始模拟单炮记录; b 加入随机噪声的单炮记录; c 小波变换阈值去噪结果; d Contourlet变换阈值去噪结果; e 本文方法去噪结果; f 本文方法去除的随机噪声

图7 本文基于Contourlet变换的K-L变换方法去噪后单炮记录频谱分析a 原始模拟单炮记录频谱; b 加入随机噪声的单炮记录频谱; c 本文方法去噪后单炮记录频谱

3 实际资料处理效果分析

采用本文基于Contourlet变换的K-L变换去噪方法对我国南方某工区实际地震资料进行了处理,如图8所示。该区单炮记录噪声比较严重(图8a),1000～2000ms的有效反射信号被噪声淹没。利用本文方法进行去噪处理后,单炮记录信噪比得到明显提高,1000～2000ms有效反射波同相轴清晰可见(图8b),去除的噪声中肉眼未见有效反射信号(图8c),说明本文方法不仅能够很好地去除地震资料中的随机噪声,而且不损伤有效信号,具有良好的保真性。

利用本文方法对整个工区的单炮记录进行叠前去噪,并分别对叠前去噪处理前、后的单炮记录进行叠加,结果如图9所示。

图8 本文去噪方法处理前、后单炮地震记录效果分析a 去噪前单炮记录; b 去噪后单炮记录; c 去除的噪声

图9 本文方法去噪处理前(a)、后(b)叠加剖面对比

对比可见,利用本文方法进行叠前去噪处理后,叠加剖面信噪比得到了显著提高,有效反射波同相轴连续性增强,波组特征明显改善。

4 结束语

本文对Contourlet系数进行K-L变换,利用最大似然估计法和多尺度噪声估计法来估算K-L变换域能量百分比函数,根据K-L变换域能量百分比函数自适应地确定K-L反变换所用的特征向量,修改Contourlet系数,去除随机噪声,提高地震资料信噪比。数据模拟和实际资料处理结果表明,本文方法不仅能很好地去除地震资料中的随机噪声,提高资料信噪比,而且不损伤有效信号,具有良好的保真性。

[1] GROSSMAN A,MORLET J. Decomposition of hardy function into square integrable wavelets of constant shape[J]. Siam Journal on Mathematical Analysis,1984,15(4):723-736

[2] MALLAT S G. Multiresolution approximations and wavelet orthonormal bases of L2(R)[J]. Transactions of the American Mathematical Society,1989,315(1):69-87

[3] DAUBECHIES I. Orthonormal bases of compactly supported wavelets[J]. Communications on Pure and Applied Mathematics,1988,41(7):909-996

[4] MALLAT S G. A theory for multiresolution signal decomposition:the wavelet representation[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence,1989,11(7):674-693

[5] CHUI C K,WANG J Z. A cardinal spline approach to wavelets[J]. Proceedings of the American Mathematical Society,1991,113(3):785-793

[6] 崔锦泰.小波分析导论[M].程正兴,译.西安:西安交通大学出版社,1995:73-79 CUI J T. An introduction to wavelets[M].CHENG Zhengxing translator.Xi’an:Xi’an Jiaotong University Press,1995:73-79

[7] 盛冠群,李振春,王维波,等.基于小波分解与高阶统计量的微地震初至拾取方法研究[J].石油物探,2015,54(4):388-395 SHENG G Q,LI Z C,WANG W B,et al. A new automatic detection method of microseismic events based on wavelet decomposition and high-order statistics [J]. Geophysical Prospecting for Petroleum,2015,54(4):388-395

[8] 王小杰,栾锡武.基于小波分频技术的地层Q值提取方法研究[J]. 石油物探,2015,54(3):260-266 WANG X J,LUAN X W. Q value extraction method based on wavelet frequency division technology[J]. Geophysical Prospecting for Petroleum,2015,54(3):260-266

[9] 尚帅,韩立国,胡玮,等.压缩小波变换地震谱分解方法应用研究[J].石油物探,2015,54(1):51-55,82 SHANG S,HAN L G,HU W,et al. Applied research of synchrosqueezing wavelet transform in seismic spectral decomposition method [J]. Geophysical Prospecting for Petroleum,2015,54(1):51-55,82

[10] 蔡剑华,熊锐.基于频率切片小波变换的时频分析与MT信号去噪[J].石油物探,2016,55(6):904-912 CAI J H,XIONG R. Magnetotelluric data denosing based on time-frequency analysis of the frequency slice wavelet transform [J]. Geophysical Prospecting for Petroleum,2016,55(6):904-912

[11] DO M N,VETTERLI M. Contourlets:a directional multiresolution image representation[J]. International Conference on Image Processing,2002,1(1):I357-I360

[12] 彭才,常智,韩朝军,等.基于Contourlet变换的地震噪声衰减[J].勘探地球物理进展,2008,31(4):274-278 PENG C,CHANG Z,HAN Z J,et al. Noise suppression of seismic data based on contourlet transform[J].Progress in Exploration Geophysics,2008,31(4):274-278

[13] 张恒磊,李名勇,刘天佑.Contourlet域相关和阈值衰减联合去噪方法及其在地震资料处理中的应用[J].武汉大学学报(信息科学版),2011,36(9):1047-1050 ZHANG H L,LI M Y,LIU T Y. Joint denoising of correlation and thresholding in contourlet domain and its application to seismic data[J]. Geomatics and Information Science of Wuhan University,2011,36(9):1047-1050

[14] 王建花,王守东,刘燕峰.基于Contourlet系数相关性的地震噪声压制方法[J].中国海上油气,2016,28(1):35-40 WANG J H,WANG S D,LIU Y F. Seismic noise suppression method based on correlation of contourlet coefficients[J]. China Offshore Oil and Gas,2016,28(1):35-40

[15] HEMON C H,MACE D. Use of the Karhunen-Loeve transformation in seismic data processing[J]. Geophysical Prospecting,1978,26(3):600-626

[16] 傅才芳,罗国安.应用K-L滤波提高地震记录的信噪比[J].石油地球物理勘探,1986,21(5):486-493 FU C F,LUO G A. K-L filtering used to raise seismic S/N ratio[J]. Oil Geophysical Prospecting,1986,21(5):486-493

[17] 杨文采.非线性K-L滤波及其在反射地震资料处理中的应用[J].石油物探,1996,35(2):17-26 YANG W C. Nonlinear K-L filtering and its application to seismic data processing[J]. Geophysical Prospecting for Petroleum,1996,35(2):17-26

[18] 张广智,印兴耀,吴国忱,等.一种提高K-L变换速度和精度的方法[J].石油物探,1997,36(增刊):112-115 ZHANG G Z,YIN X Y,WU G C,et al. A method to improve the speed and accuracy of K-L transformation[J]. Geophysical Prospecting for Petroleum,1997,36(S1):112-115

[19] LIU X W. Ground roll suppression using the Karhunen-Loeve transform[J]. Geophysics,1999,62(2):564-566

[20] 王华忠,冯波,王雄文,等.地震波反演成像方法与技术核心问题分析[J].石油物探,2015,54(2):115-125,141 WANG H Z,FENG B,WANG X W,et al. Analysis of seismic inversion imaging and its technical core issues[J]. Geophysical Prospecting for Petroleum,2015,54(2):115-125,141

[21] 王华忠,冯波,王雄文,等.特征波反演成像理论框架[J].石油物探,2017,56(1):38-49 WANG H Z,FENG B,WANG X W,et al. The theoretical framework of characteristic wave inversion imaging[J]. Geophysical Prospecting for Petroleum,2017,56(1):38-49

[22] DO M N,VETTERLI M. The Contourlet transform:an efficient directional multiresolution image representation[J]. IEEE Transactions on Image Processing,2005,4(12):2091-2106

[23] VAIDYANATHAN P P. Multirate systems and filter banks[M]. NJ:Prentice Hall,1992:3385-3388

[24] BURT P J,ADELSON E H. The Laplacian pyramid as a compact image code[J]. Readings in Computer Vision,1983,31(4):532-540

[25] BAMBERGER R H,SMITH M J T.A filter bank for the directional decomposition of images:theory and design[J]. IEEE Transactions on Signal Processing,1992,40(4):882-893

[26] DONOHO D L,JOHNSTONE I M. Ideal spatial adaptation via wavelet shrinkage[J]. Biometrika,1994,81(3):425-455

[27] 冯鹏.高分辨图像处理用抗混叠Contourlet变换的若干关键问题研究[M].重庆:重庆大学,2007:88-93 FENG P. Study on some key problems of non-aliasing Contourlet transform for high-resolution images processing[M]. ChongQing:Chongqing University,2007

[28] MA X L,ZHOU F,ZHOU X J. Medical image denoising using non-subsampled Contourlet transform and total variation model[J]. Journal of Applied Sciences,2014,32(5):481-485

[29] 付燕.人工地震信号去噪方法研究[M].西安:西北工业大学,2002:75-79 FU Y.Research on de-noising methods of seismic data[M].Xi’an:Northwestern Polytechnical University,2002:75-79

[30] YUAN X H,BUCKLES B P. Subband noise estimation for adaptive wavelet shrinkage[J].Proceedings of the 17thInternational Conference on Pattern Recognition,2004,4:885-888

[31] 齐乃新,曹立佳,杨小冈,等.基于改进邻域收缩法的非下采样Contourlet变换域红外图像去噪[J].科学技术与工程,2014,14(23):103-107 QI N X,CAO L J,YANG X G,et al. Infrared image de-noising using improved neigh-shrink based on NSCT[J]. Science Technology and Engineering,2014,14(23):103-107

[32] 李东明,盖梦野,李超然,等.基于小波域的Contourlet变换法的自适应光学图像去噪算法研究[J].激光与光电子学进展,2015,52(11):91-96 LI D M,GAI M Y,LI C R,et al. Research on adaptive optics image denoising algorithm based on the wavelet-based Contourlet transform[J]. Laser & Optoelectronics Progress,2015,52(11):91-96

(编辑：戴春秋)

Seismicrandomnoiseself-adaptiveattenuationmethodbasedonK-LtransformintheContourlet-domain

LIU Yanfeng,ZOU Shaofeng,JV Xingguo

(SinopecGeophysicalResearchInstitute,Nanjing211103,China)

After the Contourlet transform,Contourlet coefficients of reflection are large and correlative due to the rich texture and edge features of effective signals in seismic data,while the Contourlet coefficients of random noise are small and unrelated.Considering the advantage of the classification feature extraction for the K-L transform,we apply the K-L transform to Contourlet-domain coefficients.Maximum likelihood estimation and multiscale noise estimation are adopted to estimate the variance of Contourlet coefficients of effective signals and random noise in seismic records.In order to adaptively determine the number of eigenvectors used for the K-L inverse transform,the variance is applied to define the energy percentage threshold function in the K-L domain.Contourlet coefficients transform are modified.And then Contourlet inverse transform is conducted to suppress random noise.However,numerical simulation and field data processing results show that this method can effectively suppress random noise with high fidelity.

Contourlet transform,K-L transform,maximum likelihood estimation,multiscale noise estimation,random noise attenuation,self-adaptive

P631

：A

1000-1441(2017)05-0676-08DOI:10.3969/j.issn.1000-1441.2017.05.008

刘燕峰,邹少峰,居兴国.基于Contourlet变换的KL变换地震随机噪声自适应衰减方法[J].石油物探,2017,56(5):683

LIU Yanfeng,ZOU Shaofeng,JV Xingguo.Seismic random noise selfadaptive attenuation method based on KL transform in the Contourletdomain

[J].Geophysical Prospecting for Petroleum,2017,56(5):683

2016-08-08;改回日期：2016-10-28。

刘燕峰(1980—),女,工程师,主要从事地震资料处理及方法研究工作。