地质构造约束高斯束层析反演方法与应用

万 弘,杨勤勇,蔡杰雄,倪 瑶,李 辉

(1.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103;2.中国石油大学(华东)地球科学与技术学院,山东青岛266580;3.同济大学海洋与地球科学学院波现象与反演成像研究组,上海200092)

地质构造约束高斯束层析反演方法与应用

万 弘1,2,杨勤勇1,2,蔡杰雄1,倪 瑶1,李 辉3

(1.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103;2.中国石油大学(华东)地球科学与技术学院,山东青岛266580;3.同济大学海洋与地球科学学院波现象与反演成像研究组,上海200092)

高斯束层析介于射线类层析和波动方程类层析之间,兼具了计算效率高和过程稳定的优势,是速度建模的一种重要手段。但是,常规高斯束层析灵敏度矩阵建立在射线的基础上,不能遍历整个模型,求解过程不收敛。为此,建立了高斯束层析反演的完整流程,给出了高斯束层析灵敏核函数的构建方法,并且为了使层析反演过程趋于稳定且快速收敛,提出了将地质构造反射界面的倾角场和反射点的位置信息融入高斯光滑矩阵对高斯束层析矩阵进行正则化的方法。理论模型和实际地震资料测试结果验证了方法的可行性和有效性。

高斯束;灵敏核函数;地层倾角;地质构造约束;层析反演;正则化

地震波成像技术主要包括偏移成像和反演成像两个方面。偏移成像是利用观测到的地震波场记录进行逆向传播,同时消除地震波的传播效应,最后获取地下地质结构图像的过程;反演成像是根据观测数据和地球物理模型参数之间的函数关系,反演求取地球物理模型的过程[1]。因此,从本质上说,反演成像较偏移成像的应用范围更广。常规的地震反演成像可以分为层析成像、最小二乘叠前深度偏移和AVA分析3个重要的环节[2]。

理想的背景速度模型在地震勘探中十分重要[3]。目前,层析速度分析是获得精细速度模型的重要手段。理论上,层析速度分析技术主要有两个方向:基于射线理论的射线类层析[4-5]和基于波动理论的波动方程层析[6-7]。而射线束层析是近年研究的热点,其特点是介于射线类层析和波动方程层析之间,兼顾了计算效率高和相对稳定的优点,其类型主要有高斯束层析[8-9]、菲涅尔体层析[10-11]、胖射线层析[12]和高斯波包层析[13-14]等。常规的层析方法利用道集上的时差(RMO)来反映速度的扰动特点,通过改善合成数据角道集的拉平程度,来提高与观测数据之间的相似性。而常规的高斯束层析利用走时信息通过一个炮检对对应一个走时残差建立多个层析方程,可以相应降低层析方程的病态性,但是其灵敏度矩阵的建立依然基于射线理论,存在类似常规射线类层析不能遍历整个模型的问题,特别是在地质构造复杂、速度变化较快、高陡倾角处。所以,有必要在反演求解层析方程时加入正则化。

为了确保反演的稳定性,SINOQUET[15]提出在反射层析中使用先验地质信息;CLAPP等[16]将反射层析运用到共成像点道集拉平中,并指出了标准正则化的缺点。为了克服这些问题,他们提出使用沿着初始偏移剖面上的层位构建的平滑算子作为反射层的先验信息。通过沿着反射层来平滑速度模型,能够使构建的模型更加符合地质规律,反射层的定位更精确,得到效果更好的成像剖面。这些研究为正则化提供了一个思路,就是在原有的数据正则化的基础上加入额外的地质信息来减少层析方程的病态性。

本文基于高斯束叠前深度偏移理论[17-19],结合地质构造的位置信息和倾角信息构建高斯光滑矩阵对层析反演进行正则化。同时,将断层检测法与结构张量算法相结合自动拾取偏移剖面中反射点的位置和地层倾角信息,计算剩余曲率并转化为走时残差。利用这些信息构建地质构造约束的光滑矩阵和灵敏度矩阵,建立了正则化的层析方程,求解并多次迭代更新速度模型。最后利用理论模型和实际地震资料验证本文方法的有效性。

1 方法原理

1.1 基于核函数的高斯束层析

常规的走时层析将走时残差Δτ表示为慢度差Δm沿着射线路径l的线性积分形式:

(1)

该方程在实际运用过程中需要进行离散化处理,即网格层析,其特点是具有严重的病态性。而LIU等[20]给出了在RYTOV和BORN近似下走时残差的另一种表达形式:

(2)

式中:ub和up分别表示背景波场和扰动波场,二者之和为观测波场;ω为圆频率。根据高斯束正演理论,可以将波场表示为振幅和复数相位的形式,则(2)式可以表示为:

(3)

式中:ψ为加权系数;Agb,φ和tgb分别为高斯束的振幅、入射角度和相位;Aobs和tobs分别为观测数据的振幅和相位。(3)式表示总的走时残差,对于确定的高斯束φ0,其走时残差可以表示为:

(4)

至此,LI等[21]提出了将确定的高斯束φ0的走时残差与总的走时残差的比值作为高斯束敏感核函数:

(5)

在方程(1)的基础上构建灵敏度矩阵,将高斯束层析方程表达为空间积分的形式:

(6)

从方程(5)可以看出,高斯束核函数的覆盖范围是以高斯束的振幅为宽度。与常规射线层析相比,方程(6)的稀疏性更小,更加符合地震波的传播规律,可以得到更加精确的速度模型。

(7)

式中:v0(φ)表示观测点在射线φ上的投影x0沿着切线方向的速度;S0表示观测点到点x0的距离;P(s)和Q(s)为动力学射线参数。

1.2 地质构造约束正则化

为了进一步降低反演的非唯一性,本文考虑在高斯束层析反演过程中加入地质构造约束,使反演的结果更趋于稳定,并更具地质意义。具体的方法是在层析矩阵中加入光滑矩阵[23]。

常规层析方程(1)进行矩形网格离散化后得到一般的层析反演方程:

(8)

若考虑模型预条件,即Δm=Su,则层析反演方程可以表示为:

(9)

式中:L为线性化算子;S为预条件算子;u为预条件的解。考虑阻尼因子ε,则层析方程的阻尼最小二乘方程可以表示为:

(10)

将预条件下的解u=S-1Δm代入方程(10)并适当变换得到:

(11)

当预条件算子S是包含地质构造信息的光滑算子时,该方程即为地质构造约束正则化的层析方程,其对应的解为正则化后的光滑解。

所以,将地质构造信息加入构建的光滑矩阵中是地质构造约束正则化的关键点。地下介质在模型参数化后,其基本的地质规律没有改变,所以参数之间必然存在着一定的联系。层析反演中数据测量的精度由偏移剖面上的反射面倾角和在共成像点道集中拾取成像深度的精度决定。所以,地质构造中反射面的倾角信息和散射点在深度上的分布规律为地质意义上的平滑提供了一种可行的方式,而且不依赖于先验信息。

相同的空间坐标系下,不同的散射点具有不同的位置和倾角(散射点所在反射界面处的切线方向与空间坐标轴的夹角)信息,可以通过坐标变换将空间坐标系变换到局部地质坐标系来构建光滑矩阵,而这个过程可以将这些信息融入到变换后的光滑矩阵中。图1是坐标变换示意图,逆时针方向设为正方向。其中局部地质坐标系以散射点中心为原点,记为(u,v,w)T,且u轴的方向与反射界面的走向一致,w轴的方向与反射界面垂直;空间坐标系记为(x,y,z)T,通过一系列的旋转、平移可以将其变换为局部地质坐标系。若该散射点在原始空间坐标系中的坐标为(x0,

图1 三维坐标旋转示意

y0,z0)T,那么两个坐标系之间的关系可以表示为:

(12)

其中,T为旋转矩阵,满足条件:

(13)

式中:φ和θ分别表示在坐标变换过程中x和z坐标轴方向上的旋转角度。

光滑矩阵的一行是层析矩阵中描述介质点之间联系的一个光滑函数,且令此光滑函数为高斯光滑函数,考虑地质构造约束时光滑矩阵中第i行第j列的元素为:

(14)

式中:σui,σvi,σwi分别是高斯函数在局部地质坐标系中不同方向上的标准差。在实际应用过程中,地下介质一般视为层状结构,所以在平行于反射界面方向模型参数变化较小,垂直于反射界面方向的模型参数变化较大,因此对应的光滑范围前者较后者大,即σui和σvi比σwi大。这样,层析反演模型参数的空间分布特征被已知的地质特征约束。

因此,构建含地质构造信息的光滑矩阵时需要明确地质构造的倾角信息以及高斯光滑函数的标准差σui,σvi,σwi。高斯光滑函数的标准差简单易求,可以看作已知量,而地质构造的倾角信息则在自动拾取中结合结构张量算法求得。

1.3 自动拾取反射点和地层倾角

本文提出的高斯束层析反演每一次迭代都包含了深度偏移以及在偏移剖面上拾取反射点的位置和局部地层倾角等步骤。本文引入断层检测法,结合图像处理中的结构张量算法[24-25],自动拾取偏移剖面上的反射点位置以及局部地层倾角信息。

断层检测法是根据偏移剖面中反射点落在波峰或波谷上的基本特征,依据波峰或波谷处导数的绝对值最小、两侧导数符号相反的准则,初步筛选可能的反射点的高效算法。但由于地震数据中存在噪声,该方法会拾取到假的反射点。

根据断层检测法的缺陷,以及偏移剖面中反射点位于同相轴上,且该点处的图像在横向邻域范围内具有局部线性的特性,结合图像处理技术中的结构张量算法进一步筛选可能的反射点,计算局部地层倾角。局部结构张量包含图像中一点以及其邻域内信号变化的方向和对应方向上的变化大小等信息,反映了该点邻域内信号的复杂性。

该方法利用结构张量的物理意义来计算图像中任意一点的局部线性指标与局部图像切向方向(对应于地震剖面中地层的局部倾角)的单位向量。基本思想是图像上插值点的灰度值是其邻域内采样点的加权平均,并且权重不仅依赖于采样点与插值点之间的距离而且和采样点的结构(特别是其倾角)密切相关。而且,该算法会随着采样点的信号变化自适应调整权重的大小。因此,对于低信噪比数据,结构张量依然能够比较准确地反应信号的真实情况,用于拾取地下反射点和地层倾角时更加稳健。

图2为偏移剖面中部分反射点(绿色点)处自动拾取的局部地层倾角(蓝色斜线)示意图。从采样的反射点处表示局部地层倾角的斜线斜率可以看出,自动拾取的反射点基本都落在波峰上,局部地层倾角与该点处的地层走向基本一致。

图2 自动拾取的部分反射点及其对应的地层倾角示意

拾取反射点的位置坐标和地层倾角信息后,角道集的剩余曲率Δz的计算方法与一般的偏移速度分析方法一致,即利用反射点的实际深度与真实深度之间的关系得到。

1.4 地质构造约束高斯束层析反演流程

地质构造约束高斯束层析反演的实现流程如图3 所示。基于已知的初始速度模型利用高斯束正演模拟反射波,并进行高斯束深度偏移生成角道集和偏移剖面;然后自动拾取偏移剖面中的构造属性,包括反射点的位置和地层倾角,求取角道集的剩余曲率并转化为走时残差;当角道集未拉平时,根据反射点的位置坐标、地层倾角、走时残差和高斯束敏感核函数计算得到的灵敏度矩阵,构建地质构造约束的光滑矩阵S和线性化矩阵L,建立正则化层析方程;最后,求解层析方程,得到更新后的速度场。如此反复迭代优化,得到较为理想的速度模型。

图3 地质构造约束高斯束层析反演流程

2 数值实验

2.1 模型试算

实验一的目的是在理论模型中检验地质构造约束的可行性和有效性。图4a为理论速度模型,该模型背斜发育,背斜顶点处反射层数较多、纵向速度变化较大。模型的横向和纵向网格数分别为1201和601,横向和纵向网格间距分别为10m和5m。

利用平滑后的理论速度模型,结合高斯束正演得到反射地震记录(图4b),并将其视为观测数据。利用观测数据在初始速度模型(图5a)中反传,进行高斯束叠前深度偏移,得到初始的偏移剖面(图5b)。图5a中的初始速度模型视浅层为海水,即速度已知为常数,第一反射界面作为海底面并且深度已知,背斜部分的速度由浅至深按常梯度变化。在初始偏移剖面中利用自动拾取技术提取地层倾角和位置信息。图6是在初始偏移剖面上提取的反射点的位置和倾角场,被作为地质构造约束的主要依据。输入观测数据、初始速度模型以及地层倾角信息,构建高斯光滑矩阵S和线性化矩阵L,建立正则化层析方程,反演求解速度更新量,更新速度模型。更新迭代50次后得到的速度模型如图7a所示,图7b是按照上述步骤,不加入地质构造约束,层析反演迭代50次后的速度模型。对比发现:有地质构造约束时,地层层位关系更为清楚,较深处的速度与理论模型更为接近;无地质构造约束时,地层层位关系相对模糊,深部速度误差较大。图8给出了横向坐标在6km处各速度模型偏移后生成的角道集。对比发现:初始速度偏移道集存在上翘的现象(图8a),说明初始速度偏小;而经过地质构造约束的高斯束层析反演的速度模型经偏移后,角道集被拉平(图8b);且相较于无地质构造约束高斯束层析反演的速度模型经偏移后的结果(图8c),更加趋近于真实速度模型偏移后的角道集(图8d)。

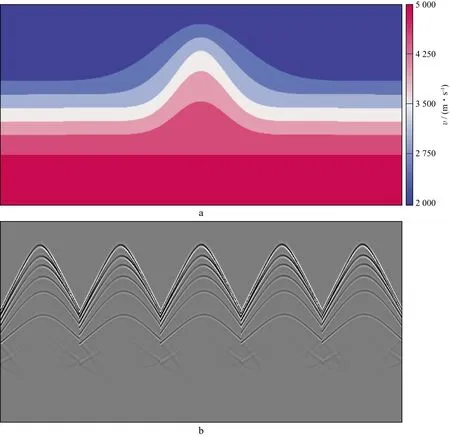
图4 多层背斜理论速度模型(a)及其正演地震记录(b)

将理论速度模型、初始速度模型、有地质构造约束和无地质构造约束迭代50次后的速度模型在横向坐标5km处的速度值抽取出来进行比较,得到不同深度的速度值如图9所示。由图9中速度与深度的关系,可以非常清晰地看出,在层析反演过程中加入地质构造约束后层析反演更新的速度模型与理论模型最为接近。无地质构造约束层析反演更新的速度模型也与理论模型接近,但其误差较大,特别是深部区域。因此,通过比较不难发现,加入地质构造约束使层析反演收敛加快,反演结果更具地质意义。

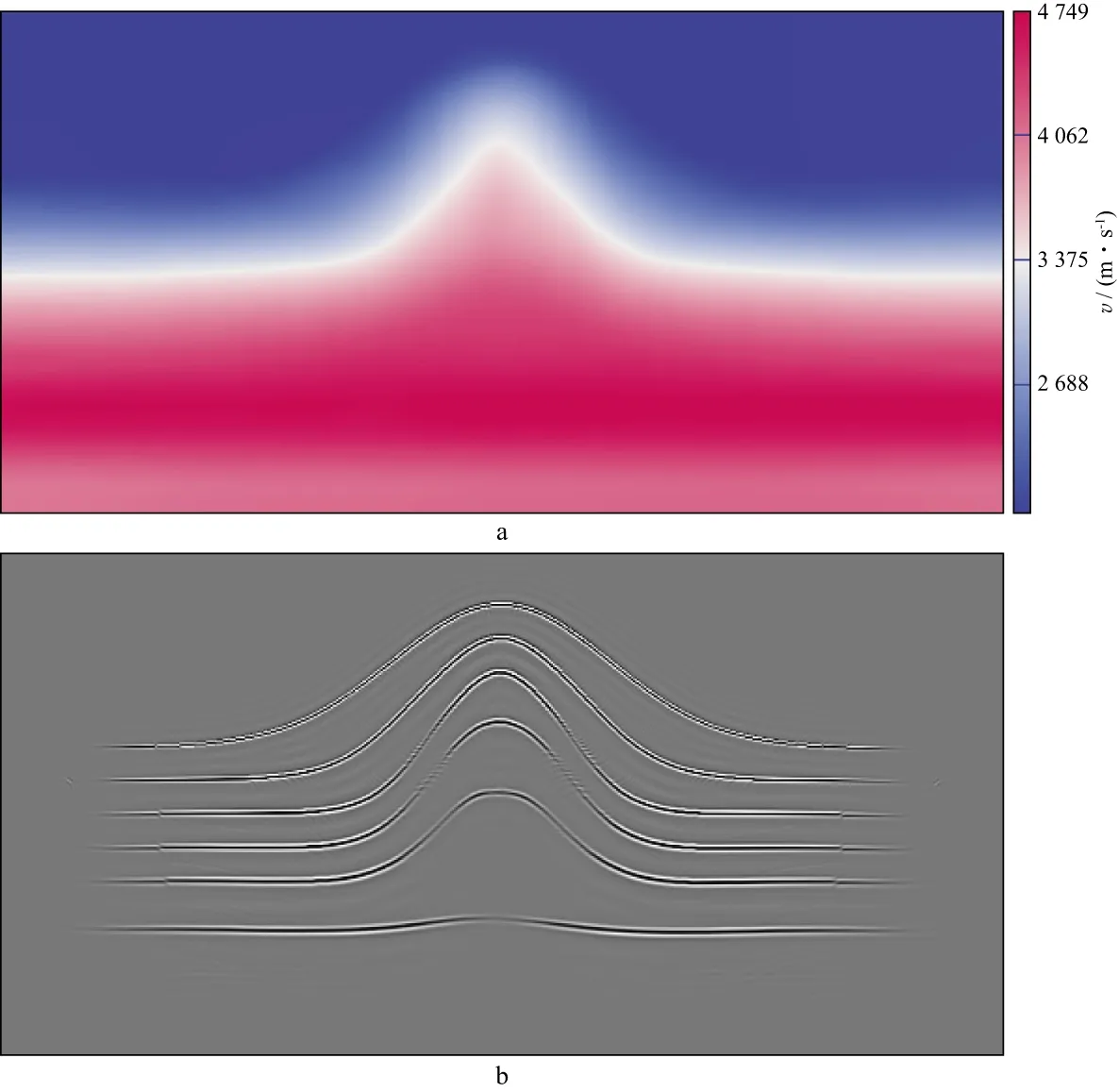
图5 初始速度模型(a)及其叠前深度偏移剖面(b)

图6 在初始偏移剖面上提取的反射点位置(a)和倾角场(b)

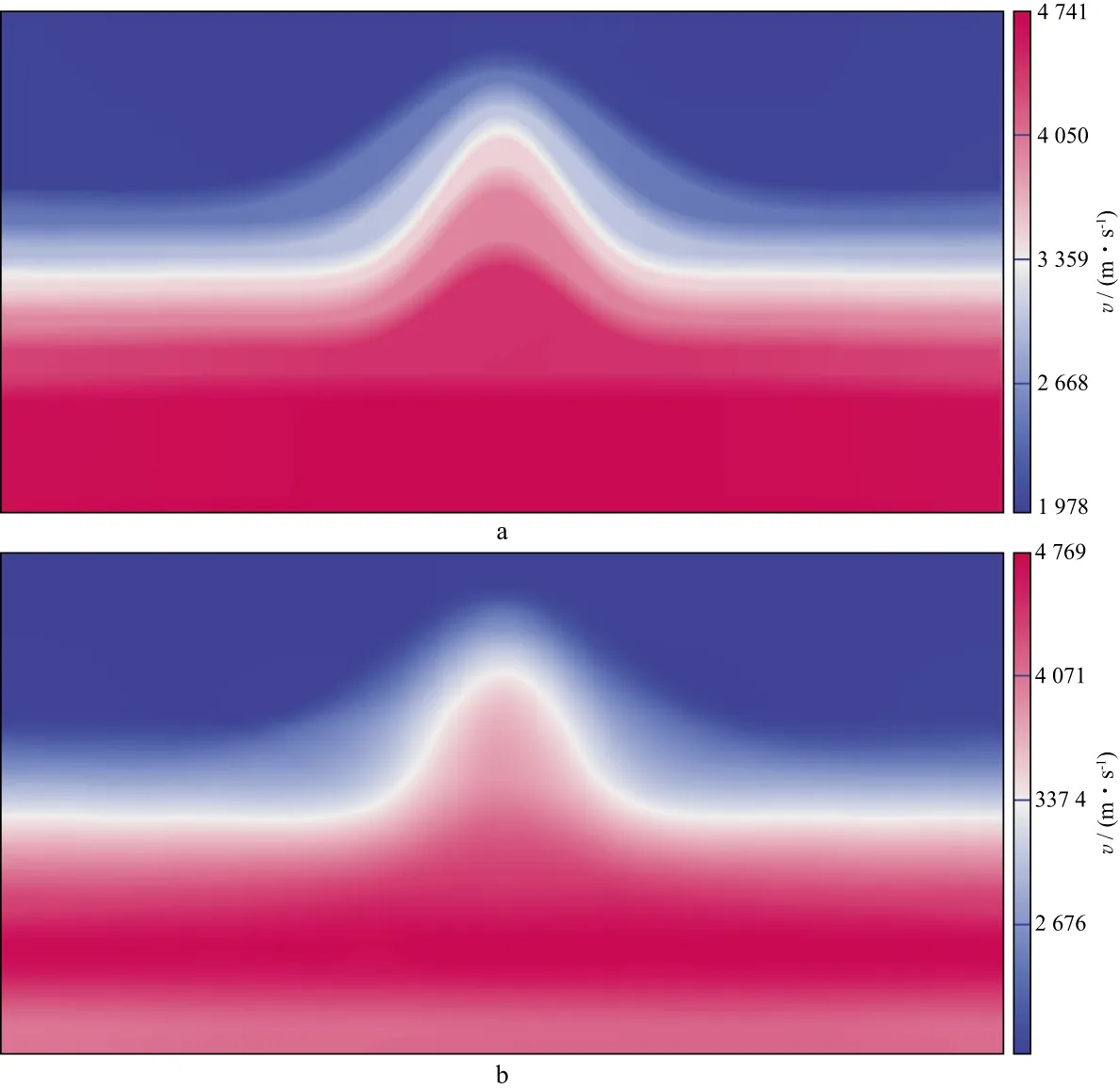
图7 有地质构造约束(a)和无地质构造约束(b)层析反演迭代50次后的速度模型

图8 横向坐标在6km处各速度模型偏移后生成的角道集a 初始角道集; b 地质构造约束高斯束层析偏移后角道集; c 无地质构造约束高斯束层析偏移后角道集; d 真实速度模型偏移后角道集

2.2 实际应用

采用华北某探区实际地震资料对本文方法进行验证。该实际地震资料共204炮,每炮60道接收,道间距50m,记录长度为6s,图10为实际炮集记录。图11a为该探区的初始建模速度场,横向和纵向的网格点数分别为405和255,横向和纵向采样间隔分别为25m和24m。地震数据的特点是浅层干扰较多,信噪比低。图11b是初始速度场对应的高斯束叠前深度偏移剖面,可见浅层薄互层成像不清晰。图12是对图11b中反射界面进行自动拾取的结果:图12a中拾取的反射点与偏移剖面上的地层比较吻合;图12b 中倾角场除了在边缘部分由于缺少同相轴不够光滑外,其余部分倾角场较为光滑;图12c是倾角场中部分点处斜率的示意图,可见自动拾取反射点处的斜率较为正确。

图9 几种速度模型在横向坐标5km处速度与深度的关系

图10 某探区实际炮集记录

图13a和图13b分别给出了在无地质构造约束和有地质构造约束情况下经过10次高斯束层析反演更新后的速度场。可以看出,在有地质构造约束的情况下速度模型反映出了更多细节信息。图14为更新后的速度场对应的高斯束叠前深度偏移剖面。由图14 可见,在有地质构造约束的情况下对应的高斯束叠前深度偏移剖面浅层中的薄互层成像效果较好,大的倾斜不整合面也能很好地反映出来。图15给出了在横向坐标为4.8km处不同速度模型偏移后生成的角道集。由图15可见,有地质构造约束方法生成的角道集多数已经被拉平,而初始速度模型和无地质构造约束方法生成的角道集还存在部分上翘的情况。速度模型和偏移剖面反映的细节特征以及角道集的拉平程度说明了本文方法运用到该实际地震资料中效果较为理想,验证了本文地质构造约束高斯束层析反演方法的有效性和实用性。

图11 初始速度模型(a)及其高斯束叠前深度偏移剖面(b)

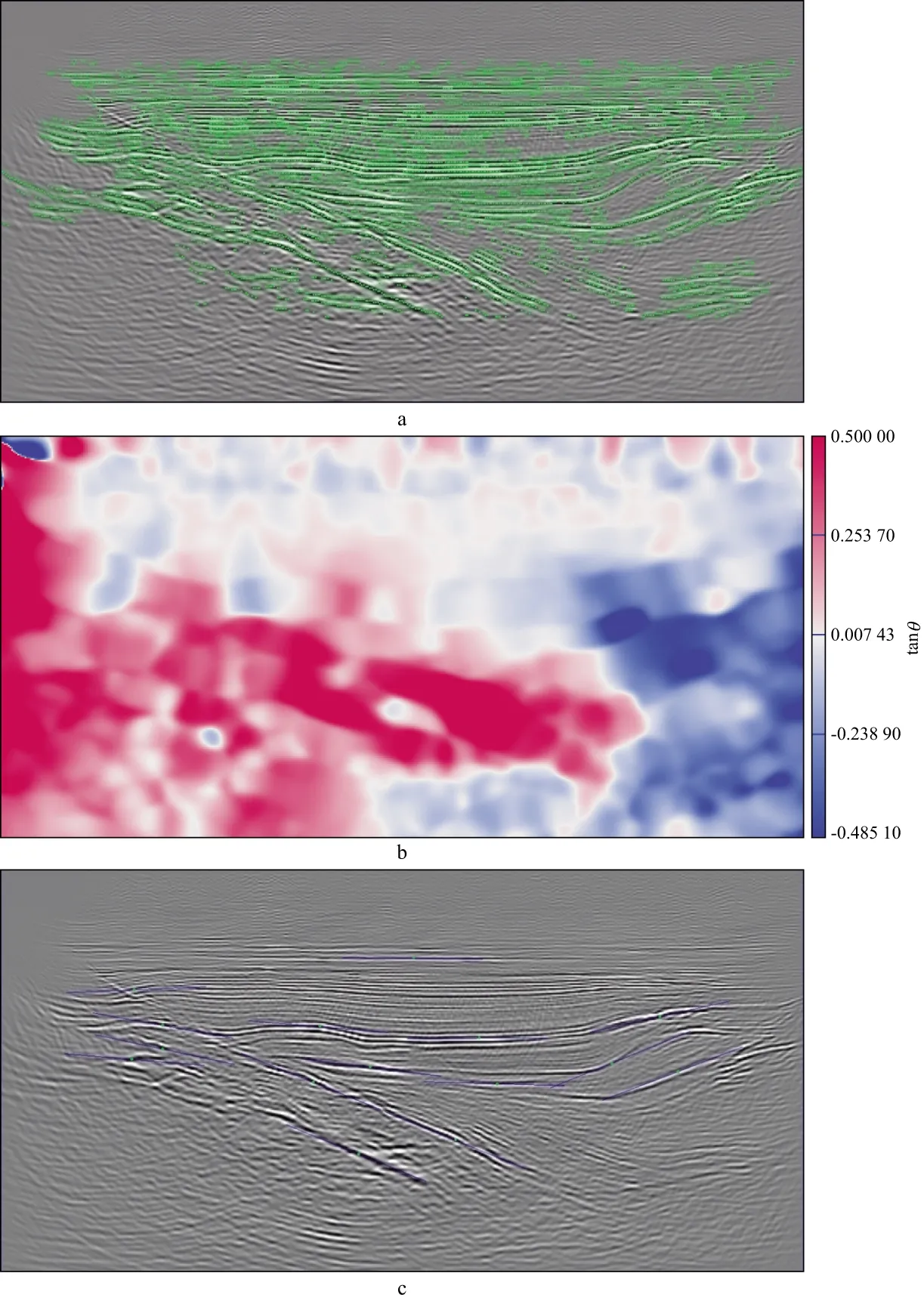
图12 对图11b中反射界面的自动拾取结果a 反射点的位置; b 倾角场; c 反射点处斜率

图13 高斯束层析反演迭代10次后的速度场a 无地质构造约束; b 有地质构造约束

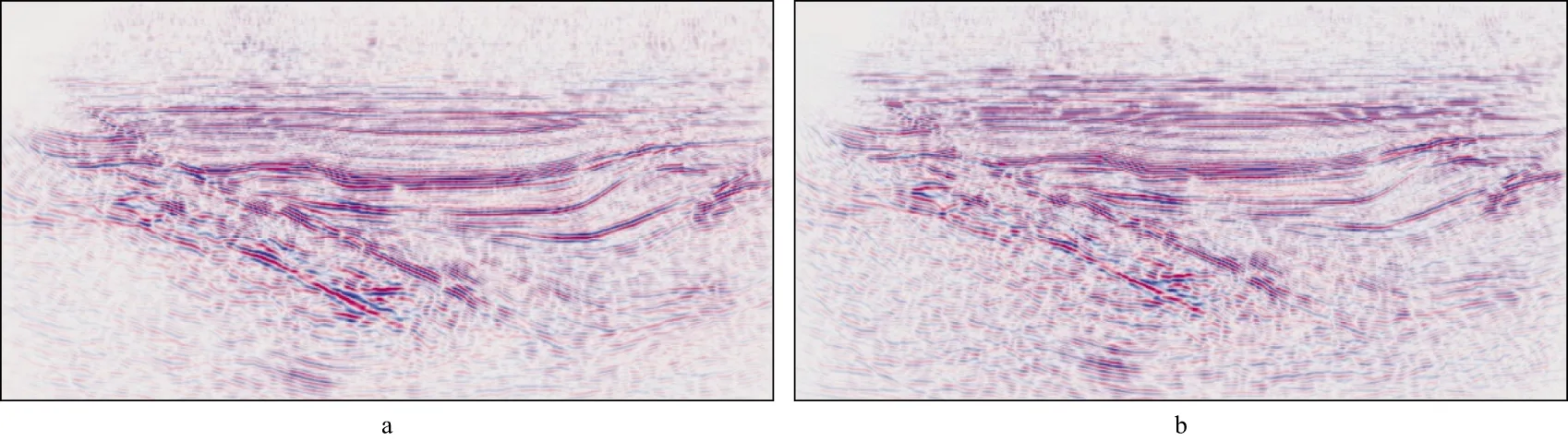
图14 更新后的速度场对应的高斯束叠前深度偏移剖面a 无地质构造约束; b 有地质构造约束

图15 横向坐标在4.8km处不同速度模型偏移后生成的角道集a 初始速度模型; b 有地质构造约束高斯束层析反演速度模型; c 无地质构造约束高斯束层析反演速度模型

3 结论

1) 本文实现了将地质构造反射界面的倾角场和反射点的位置信息融入高斯光滑矩阵中对高斯束层析矩阵进行正则化的方法,并结合走时信息构建灵敏度矩阵,建立了完整的高斯束层析速度建模流程。

2) 理论模型和实际地震资料测试得到了较为理想的速度模型,验证了本文方法的可行性和有效性,说明地质构造约束正则化方法减少了反演的非唯一性,提高了反演过程的稳定性,加快了反演收敛速度,使反演结果更具地质意义。

3) 在层析速度建模中加入地质构造信息可提高建模精度。但由于加入额外信息,增加了反演过程的计算量和数据存储量,降低了反演的计算效率,这也是该方法需要改进的地方。

[1] PARKER R L.Understanding inverse theory[J].Annual Review of Earth & Planetary Sciences,1977,5(1):35-64

[2] 王华忠,冯波,王雄文,等.地震波反演成像方法与技术核心问题分析[J].石油物探,2015,54(2):115-125 WANG H Z,FENG B,WANG X W,et al.Analysis of seismic inversion imaging and its technical core issues[J].Geophysical Prospecting for Petroleum,2015,54(2):115-125

[3] 王华忠,冯波,李辉.各种速度分析与反演方法的对比研究[J].岩性油气藏,2012,24(5):2-11 WANG H Z,FENG B,LI H.Comparison among velocity analysis and inversion methods[J].Lithologic Reservoirs,2012,24(5):2-11

[4] BISHOP T N,BUBE K P,CUTLER R T,et al.Tomographic determination of velocity and depth in laterally varying media[J].Geophysics,1985,50(6):903-923

[5] LIU Z,BLEISTEIN N.Migration velocity analysis:theory and an iterative algorithm[J].Geophysics,1995,60(1):142-153

[6] LUO Y,SCHUSTER G T.Wave-equation traveltime inversion[J].Geophysics,1991,56(5):645-653

[7] WOODWARD M J.Wave-equation tomography[J].Geophysics,1992,57(1):15-26

[8] SEMTCHENOK N M,POPOV M M,VERDEL A R.Gaussian beam tomography[J].Expanded Abstracts of 71stAnnual Internat EAGE Conference & Exhibition,2009:U032

[9] VERDEL A R,SEMTCHENOK N M,POPOV M M,et al.Nonlinear Gaussian beam tomography:a new method capable of determining highly complex velocity models[J].Expanded Abstracts of 73rdAnnual Internat EAGE Conference & Exhibition,2011:P141

[10] VASCO D W,PETERSON J E,MAJER E L.Beyond ray tomography:wavepaths and Fresnel volumes[J].Geophysics,1995,60(6):1790-1804

[11] WATANABLE T,MATSUAKA T,ASHIDA Y.Seismic traveltime tomography using Fresnel volume approach[J].Expanded Abstracts of 69thAnnual Internat SEG Mtg,1999:1402-1405

[12] HUSEN S,KISSLING E.Local earthquake tomography between rays and waves:fat ray tomography[J].Physics of the Earth & Planetary Interiors,2001,125(1/4):171-191

[13] TANG J,AUGUST L,WOODWARD M,et al.Automated travel time tomography using early-arrival Gaussian packets[J].Expanded Abstracts of International Geophysical Conference & Exposition,2014:761-765

[14] 李辉.地震波传播与反演成像的高斯波包理论及方法研究[D].上海:同济大学,2015 LI H.A study of the seismic wave propagation and inversion method using Gaussian packet[D].Shanghai:Tongji University,2015

[15] SINOQUET D.Modeling a priori information on the velocity field in reflection tomography[J].Expanded Abstracts of 63rdAnnual Internat SEG Mtg,1993:591-594

[16] CLAPP R G,BIONDI B,CLAERBOUT J F.Incorporating geologic information into reflection tomography[J].Geophysics,2004,69(2):533-546

[17] 蔡杰雄,方伍宝,杨勤勇.高斯束深度偏移的实现与应用研究[J].石油物探,2012,51(5):465-475 CAI J X,FANG W B,YANG Q Y.Realization and application of Gaussian beam depth migration[J].Geophysical Prospecting for Petroleum,2012,51(5):465-475

[18] CAI J X,FANG W B,WANG H Z.Azimuth-opening angle domain imaging in 3D Gaussian beam depth migration[J].Journal of Geophysics and Engineering,2013,10(2):109-123

[19] 蔡杰雄,王华忠,王立歆.基于三维高斯束算子解析的方位-反射角道集提取技术研究[J].石油物探,2016,55(1):76-83 CAI J X,WANG H Z,WANG L X.Azimuth-opening angle domain common-image gathers from 3D Gaussian beam migration[J].Geophysical Prospecting for Petroleum,2016,55(1):76-83

[20] LIU Y,DONG L,WANG Y,et al.Sensitivity kernels for seismic Fresnel volume tomography[J].Geophysics,2009,74(5):U35-U46

[21] LI H,WANG H Z.An effective tomography algorithm with Gaussian beam[J].Expanded Abstracts of International Geophysical Conference & Exposition,2014:701-704

[23] 李辉,王华忠,张兵.层析反演中的正则化方法研究[J].石油物探,2015,54(5):569-581 LI H,WANG H Z,ZHANG B.The study of regularization in tomography[J].Geophysical Prospecting for Petroleum,2015,54(5):569-581

[24] HALE D.Image-guided blended neighbor interpolation of scattered data[J].Expanded Abstracts of 79thAnnual Internat SEG Mtg,2009:1127-1131

[25] 邵荣峰,方伍宝,蔡杰雄,等.高斯束层析偏移速度建模方法及应用[J].石油物探,2016,55(1):91-99 SHAO R F,FANG W B,CAI J X,et al.A method of migration velocity analysis based on Gaussian beam tomography and its application[J].Geophysical Prospecting for Petroleum,2016,55(1):91-99

(编辑:陈 杰)

AmethodofgeologicalstructureconstrainedtomographicinversionbasedonGaussianbeamanditsapplication

WAN Hong1,2,YANG Qinyong1,2,CAI Jiexiong1,NI Yao1,LI Hui3

(1.SinopecGeophysicalResearchInstitute,Nanjing211103,China;2.SchoolofGeosciences,ChinaUniversityofPetroleum,Qingdao266580,China;3.WavePhenomenaandInversionImage(WPI),SchoolofOceanandEarthScience,TongjiUniversity,Shanghai200092,China)

Gaussian beam tomography is a compromise method between ray-based tomography and wave equation tomography,which has advantages of high computational efficiency and robust processing ability.However,the sensitivity matrix of the conventional Gaussian beam tomography is built on ray theory.It still cannot illuminate the whole model and the solver of Gaussian beam tomography maybe non-convergent.We have established a complete process of tomographic inversion based on Gaussian beam and proposed a construction method for sensitivity kernel of the Gaussian beam tomography.In order to guarantee stability,and accelerate the convergence of tomographic inversion process,we proposed to merge the dip field of the reflection interface and the position information of the reflection point into Gaussian smoothing matrix,which is used for the regularization of Gaussian beam tomographic matrix.From the tests of theoretical model and seismic field data,the geological structure constraints can not only reduce the uncertainty of the inversion and make the inversion process stable,but also recover more geological details,thus verifying its feasibility and effectiveness.

Gaussian beam,sensitivity kernel,formation dip,geological structure constraint,tomographic inversion,regularization

P631

：A

1000-1441(2017)05-0707-11DOI:10.3969/j.issn.1000-1441.2017.05.011

万弘,杨勤勇,蔡杰雄,等.地质构造约束高斯束层析反演方法与应用[J].石油物探,2017,56(5):717

WAN Hong,YANG Qinyong,CAI Jiexiong,et al.A method of geological structure constrained tomographic inversion based on Gaussian beam and its application

[J].Geophysical Prospecting for Petroleum,2017,56(5):717

2016-09-02;改回日期：2016-12-29。

万弘(1991—),男,硕士在读,主要从事地震波成像与层析反演研究。

国家科技重大专项(2011ZX05014-001-002)资助。

This research is financially supported by the National Science and Technology Major Project of China (Grant No.2011ZX05014-001-002).