基于稀疏约束反演谱分解的缝洞储层叠后数据去噪应用效果分析

李 倩,狄帮让,魏建新

(1.中国地震局地球物理勘探中心,河南郑州 450002;2.中国石油大学(北京)油气资源与探测国家重点实验室,北京102249;3.中国石油大学(北京)CNPC物探重点实验室,北京102249)

基于稀疏约束反演谱分解的缝洞储层叠后数据去噪应用效果分析

李 倩1,2,3,狄帮让2,3,魏建新2,3

(1.中国地震局地球物理勘探中心,河南郑州 450002;2.中国石油大学(北京)油气资源与探测国家重点实验室,北京102249;3.中国石油大学(北京)CNPC物探重点实验室,北京102249)

高质量的地震剖面对碳酸盐岩缝洞储层的流体识别、储量预测具有重要作用,因此对叠后地震数据进行去噪处理很有必要。为此,分析研究了基于稀疏约束反演谱分解的去噪方法在碳酸盐岩缝洞储层叠后地震数据中的应用效果。首先介绍了该方法的基本原理,然后分别将该方法用于数值模拟数据、物理模拟数据以及实际地震数据的处理,并分析去噪效果。在数值模拟测试中,将该方法与小波阈值去噪法的处理结果进行了比较,表明该方法具有较好的去噪性能和保幅性。物理模拟测试以及实际资料的处理结果均表明,该方法可以较好的压制碳酸盐岩缝洞储层叠后地震数据中的随机噪声和偏移噪声,使地震剖面中碳酸盐岩孔洞的弱反射特征得到突显,提高了地震数据处理成果的质量,为后续的定量解释奠定了良好的基础。

去噪;稀疏约束反演谱分解;碳酸盐岩储层;叠后地震数据;串珠状特征;稀疏特性

高质量的地震剖面更有利于碳酸盐岩缝洞储层的解释,因此有必要进行叠后地震数据的去噪处理。常用的地震数据去噪方法有中值滤波法、频域滤波法、f-k滤波法、多项式拟合法、傅里叶变换法、小波变换法和波动方程法等[1-4]。2010年,BONAR等[5]提出了将时间域数据转换到稀疏时频域的一种谱分解方法进行噪声压制。当使用该方法来达到去噪目的时,它就相当于基追踪去噪方法[6]。

目前对基于稀疏变换的去噪方法研究很多[7-11],其基本原理是地震信号在某一转换域被认为是稀疏的,这就意味着可以用少量高能量的值来代表几乎整个地震信号的能量,而噪声在该转换域被认为不聚焦,因此利用稀疏成分重构信号就可以有效地去除噪声能量。ELBOTH等[7]等将时频域去噪方法应用于海洋地震数据处理,取得了良好的效果。RODRIGUEZ等[9]提出了一种基于稀疏约束时频变换的非相关噪声衰减方法,并将之用于合成和实际的微地震数据中,去噪效果证明了该方法的优越性。HAN等[10-11]在时频域内地震数据重构方法的基础上,在指定域内设置一个门槛值,使得地震同相轴比噪声更集中且具有更强的能量,使用该时频谱对地震信号进行重构,最终成功降低了随机噪声。

地震信号在稀疏约束谱域中是稀疏的,而随机噪声与子波库无关,不会在稀疏谱中产生大的相关,因此使用稀疏约束反演谱对信号进行重构可以压制地震信号中的随机噪声。本文将基于稀疏约束反演谱分解的去噪方法用于碳酸盐岩缝洞储层叠后地震数据处理,利用数学模型、物理模型以及实际资料进行验证,结果表明该方法能够有效压制随机噪声,减少有效信号的损失。

1 方法原理

1.1 基于稀疏约束反演谱分解的去噪方法

通常,地震褶积模型能够被描述为一个地震记录由地震子波w(t)和反射系数序列r(t)的褶积再加上随机噪声n(t)组成:

(1)

式中:“*”表示褶积运算。地震褶积模型在地震勘探中有重要意义,却无法表示地震信号频率随时间的变化。因此,褶积模型被拓展为一个多子波褶积模型,即地震记录由一系列不同频率的地震子波和与之相对应的频率依赖的伪反射系数序列褶积之后相加再加上随机噪声得到,此模型被称之为非平稳地震褶积模型。

(2)

式中:k可以认为与子波主频线性相关;J表示参与计算的反射系数向量或者子波的总个数;wk(t)是主频与角标k相对应的地震子波;rk(t)是频率依赖的反射系数序列。

根据数学理论,方程(2)可以改写为:

(3)

即:

(4)

其中,Wk和rk(k∈[1J]分别是中心频率为fi的复雷克子波wk(t)形成的褶积矩阵以及与其有关的反射系数序列。矩阵D表示褶积矩阵库,由一系列不同频率的复雷克子波组成,也叫子波库。m则被认为是包含了所有伪反射系数序列的矩阵。地震记录由一系列中心频率唯一确定的子波库在特定时间被分解为不同的频率成分,得到频率依赖的反射系数矩阵m,这个反射系数矩阵就可以被认为是地震记录的时间—频率谱[5,11-14]。

如果不考虑随机噪声,频率依赖的反射系数矩阵可以直接通过对D求逆得到,即:

(5)

然而,由于D可能不可逆,用这种方法求解不太可行。另外,由于矩阵m的元素个数远大于地震记录的元素个数,因此该方程式是欠定的。为了解这个欠定方程,得到稀疏时频谱,本文采用了对反问题的解加额外约束项的方式将欠定方程转化为一个适定方程[13-17]。本文采用L1范数作为约束项来产生稀疏解,最终的目标函数为:

(6)

方程右边第一项是不适定项,起到了匹配分解结果与地震记录的作用,而右边第二项是约束项,确定了反射系数最终分布的形状。λ(λ>0)是正则化算子,主要起调节伪反射系数序列稀疏度以及控制解的稳定性的作用。

本文采用快速迭代软阈值算法[16]求得L1范数约束反问题的解m之后,再将m代入方程(4)中,即可得去噪后的地震数据:

(7)

2 方法测试与应用效果分析

为了测试和分析基于稀疏约束反演谱分解的去噪方法在碳酸盐岩储层中的应用效果,首先将该方法用于数值模拟数据中,并与小波阈值去噪方法进行比较,分析该方法的优越性。

2.1 数值模拟数据测试

设计一个用于数值模拟的碳酸盐岩孔洞储层的地质模型,如图1a所示。图中的孔洞宽为100m,高度依次是20,30,40,50,60,80,100,120m,围岩的速度和密度分别是6000m/s和2.73g/cm3,孔洞的速度和密度分别为4000m/s和2.56g/cm3。经过波动方程正演模拟和数据处理,得到了叠后地震数据。图1b 为图1a黑框部分的叠后地震数据。模型各层和孔洞的详细参数见表1。

图1 碳酸盐岩孔洞的地质模型和叠后地震剖面a 地质模型; b 对应图1a黑框内数据的叠后地震剖面

层名P波速度/(m·s-1)S波速度/(m·s-1)密度/(g·cm-3)层1450025002.50层2600030002.77层3400023002.50孔洞400020002.56

首先从图1b的叠后地震数据中提取第5个洞中心的单道数据(图2)进行处理,图3,图4和图5分别对比了不同信噪比情况下稀疏约束反演谱分解去噪与小波阈值去噪结果。由图2可见,孔洞处的地震反射特征十分明显。然后在单道数据上分别加上高斯白噪声使数据信噪比为2.0,1.0和0.5,如图3a,图4a以及图5a所示,较强的噪声对地震信号产生了影响,容易对之后的解释工作造成不良影响。对加噪后的单道地震数据进行稀疏约束反演谱分解,由稀疏约束反演谱分解时频图(图3b,图4b和图5b)可以看出,地震信号的稀疏分布具有非常好的局部性特征,地震信号的有效部分具有较强的聚焦性,而随机噪声由于与子波库不相关,在时频图上很少能够得到呈现。最后利用公式(7)对稀疏约束反演谱分解结果进行信号重构,得到重构后的地震信号(见图3c,图4c和图5c)。由于该方法只利用少量非零系数进行信号恢复,因此产生的估计信号相对干净。为了对比,利用小波阈值去噪法分别对图3a,图4a和图5a的含噪信号去噪,得到结果如图3d,图4d和图5d所示。采用的小波是db6小波函数,使用启发式阈值原则(即heursure准则)产生阈值,并进行软阈值处理。对信噪比为2.0的含噪信号进行5层分解;对信噪比为1.0的含噪信号进行6层分解;对信噪比为0.5的含噪信号进行4层分解。当初始数据的信噪比较高时,从图3和图4中可以看出基于稀疏约束反演谱分解的去噪方法去噪后孔洞处的反射振幅保持较好,反射振幅得到较好的恢复,仅在部分点有微小的振荡,而且比较光滑;而小波阈值去噪法去噪后孔洞处的反射振幅保持稍差,振荡点也较多。当初始数据的信噪比较低时,从图5可以看出,虽然基于稀疏约束反演谱分解的去噪方法去噪后振荡点较多,但是对于目标区域也就是孔洞处的反射振幅恢复较好,信号形变较小;而小波阈值去噪法去噪后虽然振荡点稍微少一些,但是孔洞处振幅恢复较差,信号形变也较大。总的来说,稀疏约束反演谱分解方法较精确地恢复了单道信号的大部分频率成分。尽管局部信号的能量稍有降低,孔洞处的反射仍然得到了较好的恢复,证明了该方法对于降低噪声的有效性。

图2 从图1b的叠后地震数据中提取的第5个洞中心的单道数据

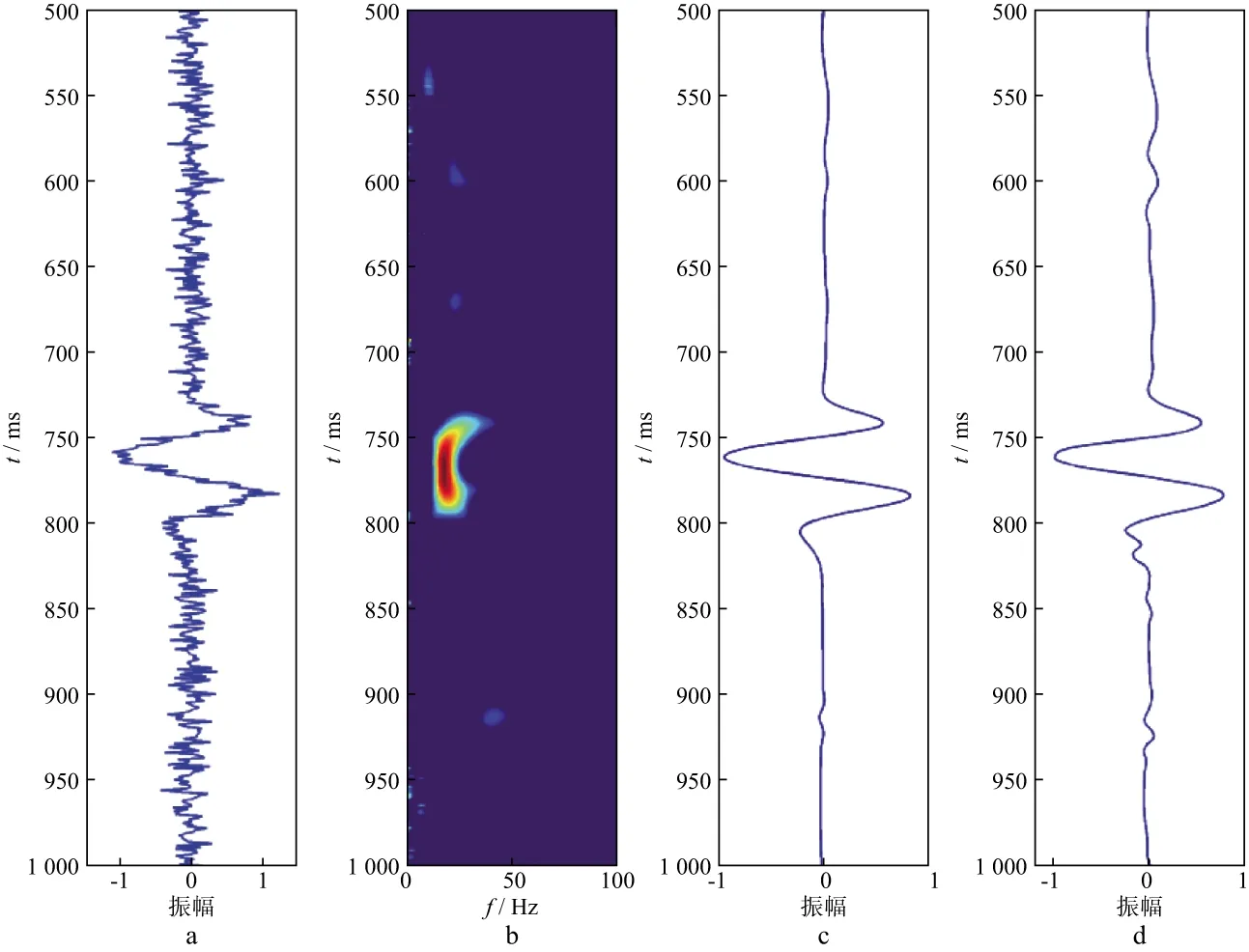
图3 信噪比为2的单道数据的稀疏约束反演谱分解去噪与小波阈值去噪结果对比a 信噪比为2的单道含噪数据; b 稀疏约束反演谱分解的时频图; c 从稀疏谱域重构的地震信号; d 小波阈值去噪结果

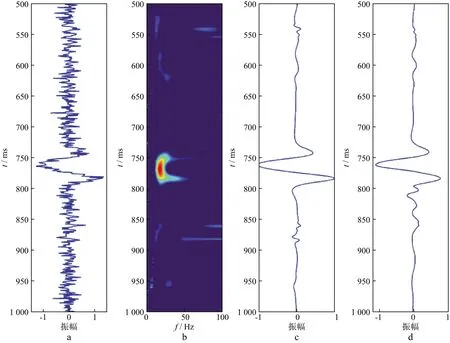
图4 信噪比为1的单道数据的稀疏约束反演谱分解去噪与小波阈值去噪结果对比a 信噪比为1单道含噪数据; b 稀疏约束反演谱分解的时频图; c 从稀疏谱域重构的地震信号; d 小波阈值去噪结果

信号的信噪比以及均方根误差通常被作为信号去噪性能的评价标准。信噪比越高,原始信号和估计信号的均方根误差越小,说明估计信号就越接近原始信号,去噪效果就越好。因此我们给出了基于稀疏约束反演谱分解去噪方法和小波阈值去噪法对不同含噪信号去噪后的信号信噪比(SNR)和均方根误差(RMSE)(如表2所示)。对比2种方法的信噪比和均方根误差,发现基于稀疏约束反演谱分解去噪方法的信噪比较小波阈值去噪法高,而均方根误差比小波阈值去噪法小,说明基于稀疏约束反演谱分解去噪方法去噪性能较好。

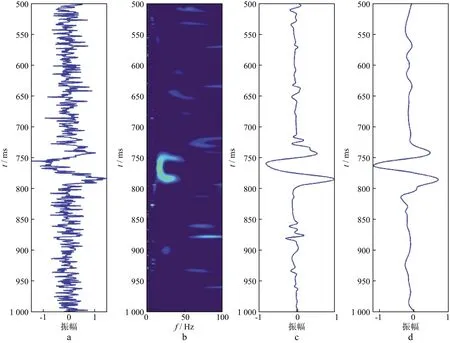
图5 信噪比为0.5的单道数据的稀疏约束反演谱分解去噪与小波阈值去噪结果对比a 信噪比为0.5的单道含噪数据; b 稀疏约束反演谱分解的时频图; c 从稀疏谱域重构的地震信号; d 小波阈值去噪结果

信号类型基于稀疏约束反演谱分解去噪小波阈值去噪SNRRMSESNRRMSE信噪比为2.0的原始信号15.98100.034413.02900.0483信噪比为1.0的原始信号14.57310.040510.03250.0683信噪比为0.5的原始信号9.29110.07438.19640.0843

为了测试该去噪方法在整个地震剖面上的应用效果,在图1b的地震剖面中提取无噪地震数据,如图6 所示,然后加上高斯白噪声使其信噪比为2.0,1.0和0.5,分别利用基于稀疏约束反演谱分解去噪方法和小波阈值去噪法进行处理,结果如图7,图8和图9所示。小波阈值去噪法选择的小波、阈值、阈值处理方法以及分解层数与处理单道数据时选择的参数相同。表3中给出了对整个地震数据分别利用2种去噪方法去噪后结果的信噪比和均方根误差。结合图7,图8,图9和表3进行综合分析,发现基于稀疏约束反演谱分解去噪方法压制噪声的效果整体上比小波阈值去噪法效果好。在初始数据的信噪比较高时,基于稀疏约束反演谱分解的去噪方法和小波阈值去噪法的去噪效果都较好,2种方法去噪后数据的信噪比和均方根误差十分接近;随着初始数据的信噪比降低,基于稀疏约束反演谱分解的去噪方法表现相对稳定,去噪后数据的信噪比和均方根误差值变化较小,而小波阈值去噪法去噪后数据的信噪比和均方根误差变化较大,去噪效果逐渐变差。在计算过程中,发现基于稀疏约束反演谱分解的去噪方法虽然压制噪声效果较好,但存在计算量大以及在求解稀疏反演谱的过程中正则化算子难以确定的缺点;而小波阈值去噪法计算速度快,但对低信噪比数据的去噪效果稍差,且阈值选择对去噪效果至关重要,要根据具体情况来选择合适的阈值。总的来说,不同的去噪方法都有其优点以及适用条件,没有哪一种方法具有普遍适用性。

图6 从图1b的叠后地震剖面中提取的无噪地震数据

图7 信噪比为2.0的数值模拟数据的稀疏约束反演谱分解去噪与小波阈值去噪结果对比a 信噪比为2.0地震数据; b 小波阈值去噪结果; c 基于稀疏约束反演谱分解去噪结果

图8 信噪比为1.0的数值模拟数据的稀疏约束反演谱分解去噪与小波阈值去噪结果对比a 信噪比为1.0的地震数据; b 小波阈值去噪结果; c 基于稀疏约束反演谱分解去噪结果

图9 信噪比为0.5的数值模拟数据的稀疏约束反演谱分解去噪与小波阈值去噪结果对比a 信噪比为0.5的地震数据; b 小波阈值去噪结果; c 基于稀疏约束反演谱分解去噪结果

信号类型基于稀疏约束反演谱分解去噪小波阈值去噪SNRRMSESNRRMSE信噪比为2.0的原始信号13.93120.011913.23210.0129信噪比为1.0的原始信号13.82730.012010.54070.0175信噪比为0.5的原始信号13.10890.01306.57240.0277

3 物理模型数据和实际数据应用效果分析

3.1 物理模型数据测试

将基于稀疏约束反演谱分解的去噪方法应用于物理模型数据,并分析其应用效果。该模型是塔里木油田哈拉哈塘地区碳酸盐岩孔洞储层地震物理模型[18],是根据相似比原理设计的与实际地层比较接近的复杂孔洞模型,其相似比分别是vm∶v=1∶2,lm∶l=1∶20000,fm∶f=10000∶1(其中,vm是模型材料的速度,v是实际地层速度,lm是模型的尺度,l是实际地层的尺度,fm是物理模拟实验中数据采集时所使用的震源的主频,f是实际地震数据的主频)。模型重点考虑了哈拉哈塘地区主要含油气层系中奥陶统一间房组至鹰山组一段上部地层,主要具有以下4个特征:①根据该地区的实际地层情况,目的层上部地层被简化为水平层状地层;②目的层之上3个相邻的上覆层整体从南向北逐渐变薄,形成尖灭;③缝洞储集体主要分布在深度为6300～7000m的地层中;④200多个不同类型的缝洞储集体被布置在水平方向上的14个缝洞区。

图10为物理模型Inline线的垂向剖面,图两侧标示了各层的深度,图中各层中的数字则表示该层的层速度和密度,并在图中标出了相应的地质层位(断层和河道未在图中标出)。

图11a是利用复杂三维地震物理模型得到的地震剖面,图11b是去噪后的地震剖面。由模型制作引起孔洞反射之间的规则干扰以及在剖面最右侧的偏移噪声(如图11中箭头所示)在很大程度上被消除,使得孔洞反射更加清晰。

3.2 实际资料应用

将基于稀疏约束反演谱分解去噪方法应用于实际碳酸盐岩缝洞储层地震剖面,并分析其应用效果。图12是目的层在3850ms到4300ms间的一个实际地震剖面,去噪后(如图12b所示),在叠加剖面上的随机噪声和剖面最右侧的偏移噪声(如箭头所示)得到了很大程度的衰减,目的层段内的构造变的更加清晰,层与层之间的信息更加丰富。剖面中间位置来自于某些孔洞的弱振幅响应和噪声混杂在一起,去噪之后,“串珠状”特征清晰可见。图13为图12中间部分的放大显示,在图13a中看到的是一片杂乱反射,无法判断是孔洞的弱反射还是干扰,而在图13b中可以清晰的看到一个个来自于孔洞的串珠状的弱反射,对后续的解释以及储层预测都能提供更好的依据。

图10 物理模型Inline线的垂向剖面

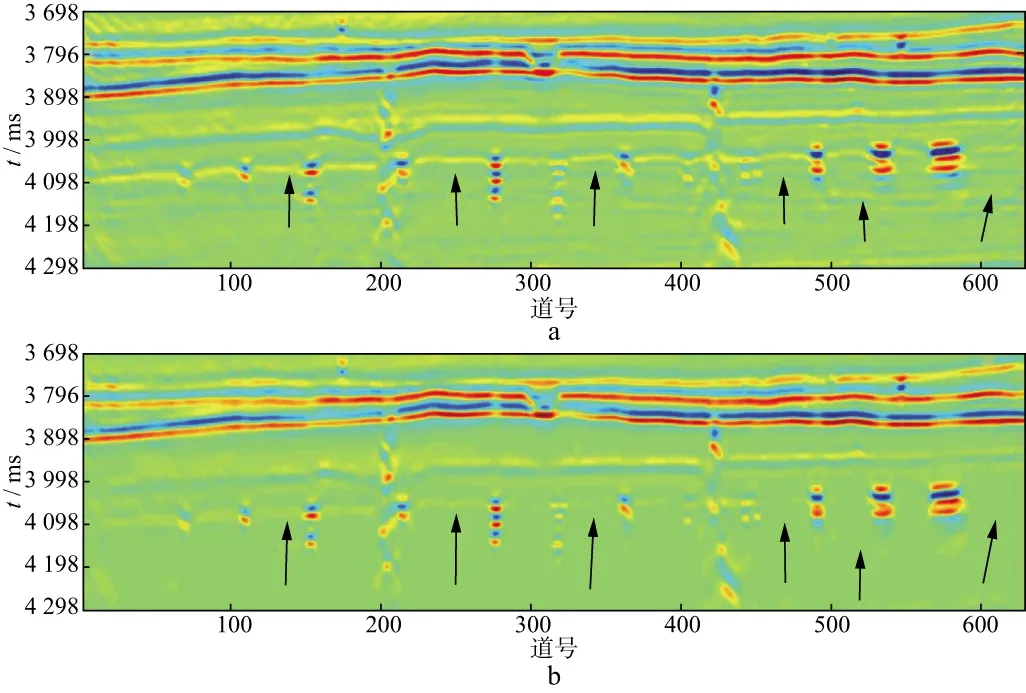
图11 物理模型数据的稀疏谱分解去噪a 去噪前的地震剖面; b 去噪后的地震剖面

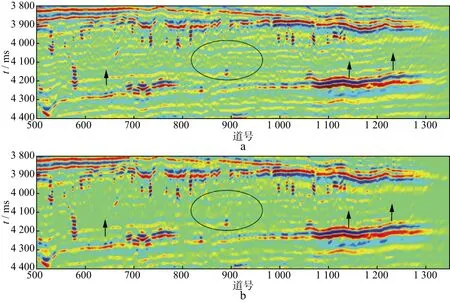
图12 实际数据的稀疏谱分解去噪a 去噪前的地震剖面; b 去噪后的地震剖面

图13 图12中间部分的放大显示a 去噪前的地震剖面; b 去噪后的地震剖面

4 结束语

本文在时频变换域中对地震信号进行稀疏分解,得到有效信号的稀疏约束反演谱,再通过稀疏约束反演谱对信号进行重构,得到衰减了随机噪声的地震记录。将基于稀疏约束反演谱分解的去噪方法用于碳酸盐岩缝洞储层叠后地震数据正演,通过数值模拟数据与小波阈值去噪法相比较,证明该方法具有较好的去噪性能。而物理模型数据及实际地震数据的去噪结果表明,该方法能够有效地去除地震剖面上的随机噪声和偏移噪声,使得孔洞反射更加清晰,而地震有效信号的能量损失较小,具有一定的保幅性。

致谢:感谢中国石油天然气股份有限公司塔里木油田分公司研究院对缝洞地震物理模型实验的支持;感谢中国石油天然气股份有限公司石油勘探开发研究院西北分院对缝洞地震物理模型数据处理的帮助！

[1] 刘婷婷,陈阳康.f-x域经验模式分解与多道奇异谱分析相结合去除随机噪声[J].石油物探,2016,55(1):67-75 LIU T T,CHEN Y K.Random noise attenuation based on EMD and MSSA in f-x domain[J].Geophysical Prospecting for Petroleum,2016,55(1):67-75

[2] 刘洋,王典,刘财,等.局部相关加权中值滤波技术及其在叠后随机噪声衰减中的应用[J].地球物理学报,2011,54(2):358-367 LIU Y,WANG D,LIU C,et al.Weighted median filter based on local correlation and its application to poststack random noise attenuation[J].Chinese Journal of Geophysics,2011,54(2):358-367

[3] 王姣,李振春,王德营.基于CEEMD的地震数据小波阈值去噪方法研究[J].石油物探,2014,53(2):164-172 WANG J,LI Z C,WANG D Y.A method for wavelet threshold denoising of seismic data based on CEEMD[J].Geophysical Prospecting for Petroleum,2014,53(2):164-172

[4] 胡天跃.地震资料叠前去噪技术的现状与未来[J].地球物理学进展,2002,17(2):218-223 HU T Y.The current situation and future of seismic data prestack noise attenuation techniques[J].Progress in Geophysics,2002,17(2):218-223

[5] BONAR D C,SACCHI M D.Complex spectral decomposition via inversion strategies[J].Expanded Abstracts of 80thAnnual Internat SEG Mtg,2010:1408-1412

[6] CHEN S B,Donoho D L,SAUNDERS M A.Atomic decomposition by basis pursuit[J].SIAM Journal on Scientific Computing,1998,20(1):33-61

[7] ELBOTH T,PRESTERUD I V,HERMANSEN D.Time-frequency seismic data de-noising[J].Geophysical Prospecting,2010,58(3):441-453

[8] SEJDIC E,DJUROVIC I,JIANG J.Time-frequency feature representation using energy concentration:an overview of recent advance[J].Digital Signal Processing,2009,19(1):153-183

[9] RODRIGUEZ I V,BONAR D,SACCHI M.Microseismic data denoising using a 3C group sparsity constrained time-frequency transform[J].Geophysics,2012,77(2):V21-V29

[10] HAN L,SACCHI M D,HAN L G.Spectral decomposition and de-noising via time-frequency and space-wavenumber reassignment[J].Geophysical Prospecting,2014,62(2):244-257

[11] 韩利.高分辨率全谱分解方法研究[D].长春:吉林大学,2013 HAN L.Research on the methods of high-resolution full spectrum decomposition[D].Changchun:Jilin University,2013

[12] PORTNIAGUINE O,CASTAGNA J.Inverse spectral decomposition[J].Expanded Abstracts of 74thAnnual Internat SEG Mtg,2004:1786-1789

[13] HAN L,HAN L G,ZHAO L.Inverse spectral decomposition with the SPGL1 algorithm[J].Journal of Geophysics and Engineering,2012,9(4):423-427

[14] 刘炳杨,李胜军,高建虎,等.最小平方约束反演谱分析方法的应用效果分析[J].石油物探,2014,53(5):562-569 LIU B Y,LI S J,GAO J H,et al.The application effects of constrained least-square spectrum analysis method[J].Geophysical Prospecting for Petroleum,2014,53(5):562-569

[15] PURYEAR C L,PORTNIAGUINE O N,COBOS C M,et al.Constrained least-squares spectral analysis:application to seismic data[J].Geophysics,2012,77(5):V143-V167

[16] BECK A,TEBOULLE M.A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J].SIAM Journal on Imaging Sciences,2009,2(1):183-202

[17] GARDNER T J,MAGNASCO M O.Sparse time-frequency representations[J].Proceedings of the National Academy of Sciences of the United States of America,2006,103(16):6094-6099

[18] 李倩,狄帮让,魏建新.碳酸盐岩储层孔洞体积的地震物理模拟估算[J].石油地球物理勘探,2014,49(6):1147-1156 LI Q,DI B R,WEI J X.Using seismic physical simulation estimate the pore volume of carbonate reservoir[J].Oil Geophysical Prospecting,2014,49(6):1147-1156

(编辑:朱文杰)

Applicationofdenoisingmethodbasedonsparseconstrainedinversespectraldecompositioninpoststackseismicdataofcave-fracturedreservoirs

LI Qian1,2,3,DI Bangrang2,3,WEI Jianxin2,3

(1.GeophysicalExplorationCenter,ChinaEarthquakeAdministration,Zhengzhou450002,China;2.StateKeyLaboratoryofPetroleumResourceandProspecting,ChinaUniversityofPetroleum,Beijing102249,China;3.CNPCKeyLabofGeophysicsExploration,ChinaUniversityofPetroleum,Beijing102249,China)

High-quality seismic sections are very important for fluid identification and reserve prediction of carbonate reservoirs.Therefore,it is necessary to suppress the noise for poststack seismic data from carbonate reservoirs.The application effect of a denoising method based on sparse constrained inverse spectral decomposition in poststack seismic data from carbonate reservoirs was analyzed.First,the basic principle of the above proposed method was introduced.Then,the proposed method was applied to numerical simulation data,physical modeling data,and field seismic data,and the application effect was analyzed.In the numerical simulation test,the proposed method was compared with the wavelet threshold denoising method,and the results proved that the proposed method has better denoising performance and amplitude preservation than the latter.The application effect of physical modeling data and field seismic data shows that this method can effectively suppress the random noise and migration noise in the stacked seismic section of a carbonate reservoir,highlight the weak reflections from some caves of a carbonate reservoir,improve the quality of the seismic data,and lay a good foundation for the subsequent quantitative interpretation.

denoisng,sparse constrained inverse spectral decomposition,carbonate reservoir,post-stack seismic data,string beads characteristic,sparse property

P631

：A

1000-1441(2017)05-0684-10DOI:10.3969/j.issn.1000-1441.2017.05.009

李倩,狄帮让,魏建新.基于稀疏约束反演谱分解的缝洞储层叠后数据去噪应用效果分析[J].石油物探,2017,56(5):693

LI Qian,DI Bangrang,WEI Jianxin,et al.Application of denoising method based on sparse constrained inverse spectral decomposition in poststack seismic data of cavefractured reservoirs

[J].Geophysical Prospecting for Petroleum,2017,56(5):693

2016-03-28;改回日期：2016-10-09。

李倩(1985—),女,工程师,博士,主要从事地震资料处理与解释方面的研究工作。

国家科技重大专项(2011ZX05007-006)项目资助。

This research is financially supported by the National Science and Technology Major Project of China (Grant No.2011ZX05007-006).