基于改进BPNN与T2全谱的致密砂岩储层渗透率预测

朱林奇,张 冲,何小菊,吴中彬,周新波,袛淑华,李 阳

(1.长江大学油气资源与勘探技术教育部重点实验室,湖北武汉430100;2.长江大学地球物理与石油资源学院,湖北武汉430100;3.中国石油天然气集团公司测井有限公司长庆事业部,陕西高陵710201;4.中国石油化工股份有限公司胜利油田有限公司桩西采油厂,山东东营257237;5.中国石油天然气股份有限公司塔里木油田分公司天然气事业部,新疆库尔勒841000;6.中国石油天然气集团公司测井有限公司华北事业部,河北任丘062552)

基于改进BPNN与T2全谱的致密砂岩储层渗透率预测

朱林奇1,2,张 冲1,2,何小菊3,吴中彬4,周新波5,袛淑华6,李 阳6

(1.长江大学油气资源与勘探技术教育部重点实验室,湖北武汉430100;2.长江大学地球物理与石油资源学院,湖北武汉430100;3.中国石油天然气集团公司测井有限公司长庆事业部,陕西高陵710201;4.中国石油化工股份有限公司胜利油田有限公司桩西采油厂,山东东营257237;5.中国石油天然气股份有限公司塔里木油田分公司天然气事业部,新疆库尔勒841000;6.中国石油天然气集团公司测井有限公司华北事业部,河北任丘062552)

针对现有核磁共振测井渗透率模型对孔隙结构复杂的致密砂岩储层预测精度不高的问题,在分析误差反向传播神经网络的缺陷后,提出了一种利用集成正则化改进神经网络(BPNN)算法与核磁共振T2全谱预测致密砂岩储层渗透率的方法。该方法采用自构形算法自动确定隐层神经元的个数,采用自适应雨林优化算法避免BP神经网络迭代陷入局部极小值,利用L2正则化算子保证算法的稳定性,采用Adaboost集成算法串联若干BP神经网络以提高模型泛化能力。提取某区致密砂岩储层192块岩样的核磁共振T2全谱数据进行建模,并应用于非建模井的渗透率评价,认为基于集成正则化改进BPNN算法评价储层渗透率精度较高,均方误差仅有0.286。

核磁共振测井;T2全谱;渗透率;集成算法;L2正则化;自适应雨林算法;集成正则化改进BPNN算法

致密砂岩储层具有强非均质性,其渗透率与储层孔隙结构关系密切,常需要利用可反映孔隙结构的核磁共振测井资料进行储层渗透率评价[1-2]。由于核磁共振测井测量的地层孔隙结构信息十分丰富,所以决定储层渗透率评价精度的关键是对核磁共振测井信息的利用程度。核磁共振测井渗透率模型大致可以分为3类：第1类是建立横向弛豫时间谱(T2全谱)划分区间与渗透率统计关系的模型[3-5];第2类是SDR及其改进模型[6];第3类是利用各种孔隙结构参数计算渗透率模型[7-13]。

对于因孔隙结构复杂导致T2全谱变化较大的致密砂岩储层来说,使用第1类模型会丢失很多区间内的信息[14-15];第2类模型采用T2全谱计算得到的孔隙结构参数表征T2全谱,所反映的微观孔隙信息有限,对于致密砂岩储层明显不适用[16];由压汞毛管压力曲线得到的孔隙结构参数与渗透率有着较好的关系,但由于实际地层含烃导致T2全谱形态发生变化,使得T2全谱中掺杂了较多的流体信息,故第3类模型预测精度较低[17]。

因此,有必要提出一种新的预测方法,该预测方法应能确定整个T2全谱与渗透率的函数关系。基于上述讨论,本文提出了结合Adaboost集成算法、L2正则化、自适应雨林算法与改进BP神经网络(BPNN)的集成正则化改进BPNN算法预测渗透率的方法,该方法将离散后的T2全谱作为输入,渗透率作为输出,通过对样本进行学习,确定输入与输出的近似函数关系并用于预测。最后利用该集成正则化改进BPNN算法对某区致密砂岩储层进行渗透率的建模预测,以检验模型的精度。

1 基于集成正则化改进BPNN算法预测渗透率的方法

BP神经网络是一种强函数逼近的监督学习算法。研究表明,神经网络具有逼近任意函数的能力,但是存在3方面的问题：收敛速度慢、隐层神经元选取具有盲目性以及容易陷入极小。为此本文尝试将Adaboost、自适应雨林算法、BP神经网络进行有机结合,克服彼此间的缺陷,得到效果较好的预测渗透率的集成正则化改进BPNN算法。首先利用Adaboost算法构建出若干BP神经网络框架(网络个数可由经验设定),在预测时由所有BP神经网络结果加权得到,这样会使得算法具有多样性及针对性,增强了神经网络的泛化能力。考虑到神经网络过于强大的函数逼近能力以及形态相似的T2全谱所计算得到的渗透率通常差异不大,在神经网络的误差函数中加入了L2正则化算子,以增加网络的稳定性。进行BP神经网络的误差反向传播迭代计算时,首先利用自适应雨林算法对BP神经网络的初始权值进行寻优,将BP神经网络权值限制在最优范围内,然后将寻优后的权值设置为初始值,输入到误差反向传播迭代算法中,迭代得到最后的权值结果,并通过自构形算法删减神经元。将几种机器学习算法进行结合,取长补短,能够从不同的角度强化模型的能力。这也是目前机器学习领域的发展趋势。对应的渗透率模型预测流程见图1。

图1 渗透率模型预测流程

1.1 改进的BP神经网络算法

由于BP神经网络在地球物理中运用比较广泛,本文不再叙述其模型构成以及学习过程,仅对BP神经网络的改进方法进行说明。BP神经网络具有收敛速度慢以及神经元选择盲目性的问题,基于上述问题本文提出两点改进措施：

1) 在神经网络学习步长中加入动量项。在BP神经网络的学习中,通常初期应该用较大的学习步长以寻找到局部最优区域,后期应该用较小的学习步长通过细微调整寻找到全局最优解。为了避免这个矛盾,在权值更新时加入动量项,起到微调权值的作用。除了加入动量项外,本文还设置了动态的学习率参数,根据迭代时每代样本输出与实际输出的误差变化改变学习率。

2) 神经网络的隐层神经元个数难以确定,往往通过试凑法得到,这具有一定的盲目性。此处利用自构形算法进行隐层神经元的合并或删除,以确定最佳BP神经网络结构[18]。

设定在隐层中神经元间相关系数与样本分散度大于门限值时进行合并,即：

(1)

式中：Rij为隐层神经元间相关系数;Qi和Qj分别为第i个神经元与第j个神经元的样本分散度;σ1,σ2为门限值,分别取为0.6～0.9与0.001～0.010。设定在隐层中神经元样本分散度小于某值时进行删除,即：

(2)

1.2 自适应雨林算法

考虑到神经网络极易陷入局部极小值,不利于确定神经网络隐层神经元个数,其初始权值及阈值不应随机选取。元启发式优化算法受到自然界各类行为启发,是模仿其群集特征的智能算法,能够利用自身或者全局的经验来搜索策略,确定最优参数。到目前为止,元启发式优化算法主要可分为4大类：①模仿自然界进化过程的算法,如遗传算法、差分进化算法等[19-21];②模仿人类行为的算法,如烟花算法、免疫算法、头脑风暴算法等[22-24];③模仿动物行为的算法,如粒子群算法、蝙蝠算法、蚁群算法、磷虾觅食算法等[25-28];④模仿植物行为的算法,如杂草算法、雨林算法等[29-30]。此处选用可避免采样过程无约束性和样本信息缺失的雨林算法作为寻优算法。针对其可能陷入局部最优的问题,尝试对其改进,提出了自适应雨林算法,即将算法中的学习因子改进为随迭代次数动态变化的学习因子,当迭代次数很小时学习因子趋近于1,当迭代次数将要达到限定次数时学习因子趋近于0,使得算法在前期具有更快的迭代速度,后期利用较慢的迭代速度寻找全局最优解：

(3)

式中：α为算法中的学习因子;t为当前迭代次数;T为设置的迭代总次数。

1.3L2正则化方法

BP神经网络存在稳定性较弱的特点,使得预测渗透率的值在T2全谱变化不大的情况下存在跳变的可能。考虑到相似T2全谱形态应存在相似的渗透率值,本文提出在目标函数中加入L2正则化项,使得模型更为稳定。加入L2正则化之后,BP神经网络的目标函数变为：

(4)

1.4Adaboost集成算法

除上述可能存在的问题之外,BP神经网络还存在过于敏感、模型泛化能力不强的问题。Adaboost为一种比较成熟、运用广泛的集成算法,能显著提高算法的精度与泛化能力[31]。将若干个BP神经网络进行组合,使神经网络之间互补,算法的最后结果由所有BP神经网络结果加权得到。对于N个训练样本((x1,y1),(x2,y2),…,(xN,yN))建立T个(具体值由人工给定)BP神经网络。之后进行样本的初始权值设定：

(5)

式中：Dt(i)表示在第t次迭代中样本的权值。

在Dt(i)下,训练弱学习器ht(x)(即第t个BP神经网络),并计算各样本误差εi及平均误差εt。利用εi及εt计算当前的弱学习器权重以及更新下次迭代(第t+1个BP神经网络)时样本权重：

(6)

式中：Wt为第t个弱学习器的权重;Dt+1(i)为第t+1个BP神经网络样本的权重。

对上述步骤迭代T次,可得到Adaboost集成预测方法。预测时,将各个弱学习器进行加权得到最终预测结果：

(7)

理论上,利用该集成正则化改进BPNN算法,能得到较其它单一非线性模型更加精确的结果。

2 实例分析

为了证明集成正则化改进BPNN算法的有效性,利用鄂尔多斯盆地临兴地区致密砂岩储层资料进行方法验证。选择7口井192块岩样进行物性实验,确定岩样渗透率,并提取对应深度核磁共振测井T2全谱。首先需对输入输出数据进行归一化,主要作用有3个：使模型快速收敛、避免模型对相对较小的输入不敏感以及避免陷入局部极小值。将测得的T2全谱横坐标(横向弛豫时间)在对数坐标轴下离散化(均分)为30个或64个孔隙度分量。选择将核磁共振测井测得的离散化T2全谱纵坐标(见图2,由于不同深度T2全谱的采样点横向弛豫时间固定,所以仅将若干个孔隙度分量值作为若干维输入即可反映整个T2全谱的形态)视为30维或64维数据并进行归一化,作为模型的输入。

对应的训练样本的教师信号(渗透率)范围见图3。

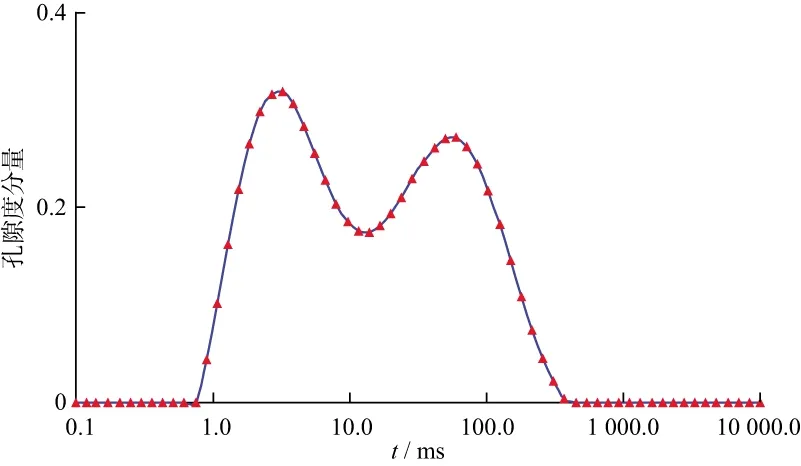
图2 离散化T2

图3 训练样本教师信号

从图3中可以看出,对于训练样本来说,其渗透率大多分布在小于0.5×10-3μm2的范围内,表明该区储层为低渗-特低渗储层。结合该区以次生孔隙为主、成岩作用强烈的实际情况,认为该地区储层渗透率计算较为困难[32-33]。

将归一化后岩心实验渗透率作为模型的输出。归一化公式为：

(8)

将数据进行归一化之后,利用集成正则化改进BPNN神经网络寻优时,除了选择的自适应雨林算法之外,选用了混合遗传算法[21]、基于讨论机制的头脑风暴算法[24]、基于对立搜索与混沌变异的磷虾觅食优化算法[28]、蚁群优化算法[25]、粒子群优化算法[27]以及未改进的雨林算法[30]编程实现。算法设置迭代次数均为2000次。考虑到优化算法中的参数对算法结果影响巨大,在调节参数时选用“固定程序训练时间”思路,通过调整各算法参数将所有优化算法对应的训练时长调节到45000s左右,以保证对比的有效性。考虑到优化算法对每一个神经网络优化结果不同,取所有神经网络优化结果的平均样本总误差变化值成图(图4)。

由图4可以看出,并不是所有的优化算法都适应于神经网络算法的寻优。自适应雨林算法的稳定性与寻优结果是7种算法中最好的,这也说明了前面理论分析的正确性。由于图4中显示的是平均总误差,可以看出在寻优算法迭代结束后,网络的最后平均总误差仍然较高,但是最终预测效果较好,说明Adaboost集成算法具有很强的提高模型预测精度的能力,这也是本文算法优于其它算法的原因。

图4 优化算法寻优效果对比

由于Adaboost算法的特性,样本对不同神经网络权值有差异。通过模拟,各神经网络神经元个数为12～18,在Adaboost算法中的权重为0.018～0.027。同时,利用1隐层20隐神经元的BP神经网络模型与核极限学习机同时进行学习,利用K-CV方式,将192块岩样数据均分为4组进行交叉验证,确定核极限学习机(选用较为常用的高斯核)正则化系数为225.2、核参数为24。通过对训练样本进行回判,BP神经网络模型、核极限学习机模型、集成改进BPNN模型和集成正则化改进BPNN模型计算相对误差分别为0.721,0.022,0.020,0.018。BP神经网络的训练精度较差,核极限学习机、集成改进BPNN与集成正则化改进BPNN效果比较接近,其中集成正则化改进BPNN效果略好于其它2种。上述3种算法效果均好于BP神经网络。这3种算法的优劣需要利用预测样本去检验。

用Timur-Coates模型、SDR模型建立预测渗透率模型进行验证井处理。SDR模型与Timur-Coates模型的渗透率计算公式分别为：

(9)

式中：KSDR为由SDR模型计算得到的渗透率;KTC为由Timur-Coates模型计算得到的渗透率;T2LM为T2的几何平均值;φ为孔隙度;m1,m2,m3,n1,n2,n3为地区经验系数;FFI为可动流体孔隙度;BVI为束缚流体孔隙度。

将公式(9)取对数进行最小二乘法求解,利用该地区39块岩样核磁共振实验数据确定m1,m2,m3,n1,n2,n3分别为0.0001577,4.2540000,0.0245000,0.0023560,3.1660000,1.2210000。为了评价上述各模型的泛化能力,尝试对验证井(XX1井、XX2井)进行渗透率评价(图5,图6,图中KCORE代表由岩心物性实验得到的空气渗透率;KAR2BP为利用集成正则化改进BPNN算法得到的储层渗透率;KARBP为利用集成改进BPNN算法得到的储层渗透率;KKELM为利用核极限学习机算法得到的储层渗透率;KBP为由BP神经网络算法得到的储层渗透率;KTC为由Timur-Coates模型得到的储层渗透率;KSDR为由SDR模型得到的储层渗透率。)。

对比可以发现,利用机器学习算法(集成正则化改进BPNN算法、集成改进BPNN算法、核极限学习机、BP神经网络)预测的储层渗透率精度明显高于传统的Timur-Coates模型与SDR模型。就4种机器学习算法来说,集成正则化改进BPNN算法与集成改进BPNN算法稳定性强,未出现其它机器学习算法出现的过于敏感的问题,在XX1井的1077～1082m深度段尤其明显。其次,从1098～1105m深度段可明显看出,集成正则化改进BPNN算法与集成改进BPNN算法泛化能力更强,准确地预测出了储层渗透率的变化趋势与渗透率值,评价精度较其它方法更高。最后,对比集成正则化改进BPNN算法与集成改进BPNN算法可以看出,正则化对算法的精度有所提高,尤其对于存在横向弛豫时间比较大的小谱时(比如XX1井1078m左右以及1099～1100m深度段、XX2井1372～1373m深度段),正则化算子可以起到控制曲线预测结果的作用,使得曲线的抖动更小,预测结果更平滑,更符合实际情况。

图5 XX1井处理结果

图6 XX2井处理结果

提取岩心深度点所对应的预测渗透率值,并计算预测误差。图7为XX1井与XX2井116个样本采用不同方法得到的预测渗透率值。BP神经网络算法、核极限学习机算法、集成改进BPNN算法和集成正则化改进BPNN算法计算的相对误差分别为1.006,0.748,0.309,0.286。由图7可见,集成正则化改进BPNN算法的效果更好,相对误差仅为0.286,高于BP神经网络算法与核极限学习机算法。由此可见,提升弱学习器与模型集成两种思路得到的模型具有很强的预测稳定性,预测出的渗透率精度较高。

图7 样本预测结果

3 结论

分析了现有核磁共振测井渗透率模型,认为没有正确反映整个T2全谱与渗透率的关系是精度不高的主要原因。对于孔隙结构复杂的储层,尽可能多地利用T2全谱中孔隙结构信息是准确评价渗透率的前提。

为了确定T2全谱与渗透率的函数关系,以离散后T2全谱作为输入,渗透率作为输出,利用集成正则化改进BPNN算法进行学习。实际资料的处理及结果分析认为,自适应雨林算法较好地解决了神经网络容易陷入极小值的问题,而Adaboost集成算法通过增加BP神经网络数提高了模型的泛化能力,使其对预测井的预测精度高于其它模型。同时,由于L2正则化算子的存在,预测得到的渗透率曲线更为稳定。与其它算法的预测结果对比表明本文提出的算法精度更高,可准确地预测储层渗透率值。

[1] 刘倩,印兴耀,李超.含不连通孔隙的致密砂岩储层岩石弹性模量预测方法[J].石油物探,2015,54(6):635-642 LIU Q,YIN X Y,LI C.Rock elastic modulus estimation for tight sandstone reservoirs with disconnected pores[J].Geophysical Prospecting for Petroleum,2015,54(6):635-642

[2] 洪忠,张猛刚,朱筱敏.基于岩石物理的致密碎屑岩气藏岩性及流体概率预测[J].石油物探,2015,54(6):735-744 HONG Z,ZHANG M G,ZHU X M.Prediction on lithology and fluid probabilities of tight clastic gas reservoir based on rock physics[J].Geophysical Prospecting for Petroleum,2015,54(6):735-744

[3] COATES G R,MARSCHALL D,MARDON D,et al.A new characterization of bulk-volume irreducible using magnetic resonance[R].Texas,USA:SPWLA,1997

[4] 邵维志,解经宇,迟秀荣,等.低孔隙度低渗透率岩石孔隙度与渗透率关系研究[J].测井技术,2013,37(2)：149-153 SHAO W Z,XIE J Y,CHI X R,et al.On the relation of porosity and permeability in low porosity and low permeability rock[J].Well Logging Technology,2013,37(2):149-153

[5] TREVIZAN W,COUTINHO B,NETTO P,et al.Magnetic resonance(NMR) approach for permeability estimation in carbonate rocks[R].Rio de Janeiro,Brazil:Offshore Technology Conference,2015

[6] KENYON W E,DAY P I,STRALEY C,et al.A three-part study of NMR logitudinal relaxation properties of water-saturated sandstones[R].Rio de Janeiro,Brazil:SPE,1988

[7] 肖忠祥,肖亮.基于核磁共振测井和毛管压力的储层渗透率计算方法[J].原子能科学技术,2008,42(10)：868-871 XIAO Z X,XIAO L.Method to calculate reservoir permeability using nuclear magnetic resonance logging and capillary pressure data[J].Atomic Energy Science and Technology,2008,42(10):868-871

[8] 肖亮,刘晓鹏,毛志强.结合NMR和毛管压力资料计算储层渗透率的方法[J].石油学报,2009,30(1):100-103 XIAO L,LIU X P,MAO Z Q.A computation method for reservoir permeability by combining NMR log and capillary pressure data[J].Acta Petrolei Sinica,2009,30(1):100-103

[9] XIAO L,MAO Z Q,WANG Z N,et al.Comparison study of models for calculating absolute permeability using nuclear magnetic resonance imaging log technology in tight sandstone gas zones[R].Kuwait City,Kuwait:SPE,2009

[10] LI C L,ZHOU C C,LI X,et al.A novel model for assessing the pore structure of tight sands and its application[J].Applied Geophysics,2010,7(3):283-291

[11] 成志刚,罗少成,杜支文,等.基于储层孔喉特征参数计算致密砂岩渗透率的新方法[J].测井技术,2014,38(2):185-189 CHENG Z G,LUO S C,DU Z W,et al.The method to calculate tight sandstone reservoir permeability using pore throat characteristic parameters[J].Well Logging Technology,2014,38(2):185-189

[12] XIAO L,LIU X P,ZOU C C,et al.Comparative study of models for predicting permeability from nuclear magnetic resonance(NMR) logs in two chinese tight sandstone reservoirs[J].Acta Geophysica,2014,62(1):116-141

[13] 肖忠祥,肖亮,张伟.利用毛管压力曲线计算砂岩渗透率的新方法[J].石油物探,2008,47(2):204-207 XIAO Z X,XIAO L,ZHANG W.A new method for calculating sandstone permeability by using capillary pressure curves[J].Geophysical Prospecting for Petroleum,2008,47(2):204-207

[14] 任晓霞,李爱芬,王永政,等.致密砂岩储层孔隙结构及其对渗流的影响[J].石油与天然气地质,2015,36(5):774-779 REN X X,LI A F,WANG Y Z,et al.Pore structure of tight sand reservoir and its influence on percolation[J].Oil & Gas Geology,2015,36(5):774-779

[15] 李召成,孙建孟,耿生臣,等.应用核磁共振测井T2谱划分裂缝型储层[J].石油物探,2001,40(4):113-118 LI Z C,SUN J M,GENG S C,et al.Classification of fractured reservoirs byT2spectrum of nuclear magnetic resonance log[J].Geophysical Prospecting for Petroleum,2001,40(4):113-118

[16] 朱林奇,张冲,胡佳,等.基于单元体模型的核磁共振测井渗透率评价方法[J].石油钻探技术,2016,44(4):120-126 ZHU L Q,ZHANG C,HU J,et al.An NMR logging permeability evaluation method based on the representative elementary volume model[J].Petroleum Drilling Techniques,2016,44(4):120-126

[17] 肖飞,何宗斌,周静萍.核磁共振测井连续表征储层孔隙结构方法研究[J].石油与天然气学报,2016,44(4):120-126 XIAO F,HE Z B,ZHOU J P.A research of successively characterizing reservoir pore structures with NMR logging data[J].Journal of Oil and Gas Technology,2016,44(4):120-126

[18] 任培罡,尹军强,杨加太,等.测录井结合神经网络流体识别技术在高邮凹陷阜宁组的应用[J].测井技术,2015,39(2):241-246 REN P G,YIN J Q,YANG J T,et al.Application of fluid identification based on the neural networks by combination of wireline and mud logging in funing formation,gaoyou sag[J].Well Logging Technology,2015,39(2):241-246

[19] 李智强,范宜仁,邓少贵,等.基于改进差分进化算法的阵列侧向测井反演[J].吉林大学学报:地球科学版,2010,40(5):1199-1204 LI Z Q,FAN Y R,DENG S G,et al.Inversion of array laterolog by improved difference evolution [J].Journal of Jilin University:Earth Science Edition,2010,40(5):1199-1204

[20] 王婧慈,郭海敏.基于标准层及改进遗传算法的剩余油测井评价[J].测井技术,2012,36(5):537-542 WANG J C,GUO H M.On the remaining oil log evaluation based on standard layer and improved adaptive genetic algorithm[J].Well Logging Technology,2012,36(5):537-542

[21] 宋欢,胡耀垓,赵正予,等.基于混合遗传算法的斜测电离图参数反演[J].地球物理学报,2014,57(3)：703-714 SONG H,HU Y H,ZHAO Z Y,et al.Inversion of oblique ionograms based on hybrid genetic algorithm[J].Chinese Journal of Geophysics,2014,57(3):703-714

[22] 罗红明,王家映,朱培民,等.基于免疫算法的地球物理反演研究[J].石油地球物理勘探,2008,43(2):222-228 LUO H M,WANG J Y,ZHU P M,et al.Study of geophysical inversion based on immunity algorithm[J].Oil Geophysical Prospecting,2008,43(2):222-228

[23] 曹炬,贾红,李婷婷.烟花爆炸优化算法[J].计算机工程科学,2011,33(1):138-141 CAO J,JIA H,LI T T.A fireworks explosion optimization algorithm[J].Computer Engineering&Science,2011,33(1):138-141

[24] 杨玉婷,史玉回,夏顺仁.基于讨论机制的头脑风暴优化算法[J].浙江大学学报:工学版,2013,47(10):1705-1711 YANG Y T,SHI Y H,XIA S R.Discussion mechanism based brain storm optimization algorithm[J].Journal of Zhejiang University:Engineering Science,2013,47(10):1705-1711

[25] 张进,安振芳,邢磊.基于混沌蚁群算法的弹性阻抗反演[J].石油物探,2015,54(6):716-723 ZHANG J,AN Z F,XING L.Elastic impedance inversion based on chaos ant colony algorithm[J].Geophysical Prospecting for Petroleum,2015,54(6):716-723

[26] 谢健,周永权,陈欢.一种基于Lévy飞行轨迹的蝙蝠算法[J].模式识别与人工智能,2013,26(9):829-837 XIE J,ZHOU Y Q,CHEN H.A bat algorithm based on lévy flights trajectory[J].Pattern Recognition and Artificial Intelligence,2013,26(9):829-837

[27] 程九龙,李明星,肖艳丽,等.全空间条件下矿井瞬变电磁法粒子群优化反演研究[J].地球物理学报,2014,57(10):3478-3484 CHENG J L,LI M X,XIAO Y L,et al.Study on particle swarm optimization inversion of mine transient electromagnetic method in whole-space[J].Chinese Journal of Geophysics,2014,57(10):3478-3484

[28] 王磊,张汉鹏,张东宁.基于对立搜索和混沌变异的磷虾觅食优化算法[J].控制与决策,2015,30(9):1617-1622 WANG L,ZHANG H P,ZHANG D N.An improved krill herd algorithm based on oppositional searching and chaos mutation[J].Control and Decision,2015,30(9):1617-1622

[29] 张氢,陈丹丹,秦仙蓉.杂草算法的收敛性分析及其在工程中的应用[J].同济大学学报：自然科学版,2010,38(11):1689-1693 ZHANG Q,CHEN D D,QIN X R.Convergence analysis of invasive weed optimization algorithm and its application in engineering[J].Journal of Tongji University:Natural Science,2010,38(11):1689-1693

[30] 高维尚,邵诚,高琴.群体智能优化中的虚拟碰撞:雨林算法[J].物理学报,2013,62(19):190202 GAO W S,SHAO C,GAO Q.Pseudo-collision in swarm optimization algorithm and solution:rain forest algorithm[J].Acta Physica Sinica,2013,62(19):190202

[31] FREUND Y,SCHAPIRE R E.A decision-theoretic generalization of on-line learning and an application to boosting[J].Journal of Computer and System Sciences,1997,55(1):119-139

[32] 赵达,许浩,汤达祯,等.临兴地区下石盒子组致密砂岩储层成岩作用及有利成岩相研究[J].科技通报,2016,32(7):30-35 ZHAO D,XU H,TANG D Z,et al.Diagenesis and favorable diagenetic analysis on the tight sandstone reservoirs of the Lower Shihezi Formation in Linxing Area[J].Bulletin of Science and Technology,2016,32(7):30-35

[33] 陈程,文晓涛,郝亚炬,等.基于White模型的砂岩储层渗透率特性分析[J].石油地球物理勘探,2015,50(4):723-729 CHEN C,WEN X T,HAO Y J,et al.Sandstone reservoir permeability characteristics analysis based on White model[J].Oil Geophysical Prospecting,2015,50(4):723-729

(编辑：陈 杰)

PermeabilitypredictionoftightsandstonereservoirbasedonimprovedBPNNandT2full-spectrum

ZHU Linqi1,2,ZHANG Chong1,2,HE Xiaoju3,WU Zhongbin4,ZHOU Xinbo5,DI Shuhua6,LI Yang6

(1.KeyLaboratoryofExplorationTechnologiesforOilandGasResources,MinistryofEducation,YangtzeUniversity,Wuhan430100,China;2.GeophysicsandOilResourceInstitute,YangtzeUniversity,Wuhan430100,China;3.ChangqingDivision,CNPCLogging,Gaoling710201,China;4.ZhuangxiOilProductionPlant,SINOPECShengliOilfield,Dongying257237,China;5.NaturalGasDivision,TarimOilfield,CNPC,Korla841000,China;6.HuabeiDivision,CNPCLogging,Renqiu062552,China)

In view of the difficulty of the existing NMR logging permeability model in the prediction of a tight sandstone reservoir with complex pore structures,after analyzing the defects of the back-propagation neural network (BPNN),we propose a method for predicting the permeability of tight sandstone reservoirs by using the BPNN algorithm improved by integrated regularization and discrete NMRT2full-spectrum data.For this method,a self-shaping algorithm is employed to automatically determine the number of hidden neurons,an adaptive rainforest optimization algorithm is used to avoid the BPNN iterations into local minimum values,theL2regularization technique is used to guarantee the algorithm stability,and the AdaBoost algorithm is used to concatenate several BPNNs to improve the generalization ability of the model.Discrete NMRT2full-spectrum data were extracted from 192 samples of tight sandstone reservoirs in a certain area for model building,which was used to predict the permeability of non-modeling wells.The results showed that it was more accurate to use the BPNN algorithm improved by integrated regularization in evaluating reservoir permeability,with a mean squared error of 0.286 only.

NMR Logging,T2full-spectrum,permeability,integration algorithm,L2regulation,adaptive rain forest optimization algorithm,BPNN improved by integrated regularization

P631

：A

1000-1441(2017)05-0727-08DOI:10.3969/j.issn.1000-1441.2017.05.013

朱林奇,张冲,何小菊,等.基于改进BPNN与T2全谱的致密砂岩储层渗透率预测[J].石油物探,2017,56(5):734

ZHU Linqi,ZHANG Chong,HE Xiaoju,et al.Permeability prediction of tight sandstone reservoir based on improved BPNN and T2 fullspectrum

[J].Geophysical Prospecting for Petroleum,2017,56(5):734

2016-09-13;改回日期：2017-02-21。

朱林奇(1993—),男,博士在读,主要从事岩石物理研究、机器学习的地球物理运用研究以及地球物理测井解释与评价工作。

张冲(1983—),男,副教授,主要从事地球物理测井解释与评价工作。

湖北省自然科学基金项目(2013CFB396)与中国石油天然气集团公司重大专项(2013E-38-09)共同资助。

This research is financially supported by the Natural Science Foundation of Hubei Province,China (Grant No.2013CFB396) and Major project of China National Petroleum Corporation (Grant No.2013E-38-09).