基于风电场输出功率波动特性分析的本征时间尺度的确定

时 彤，姜 卓，肖 白

(1.大唐东北电力试验研究所有限公司，吉林 长春 130012； 2.北华大学计算机科学与技术学院，吉林 吉林 132021； 3.东北电力大学电气工程学院，吉林 吉林 132012)

基于风电场输出功率波动特性分析的本征时间尺度的确定

时 彤1，姜 卓2，肖 白3

(1.大唐东北电力试验研究所有限公司，吉林 长春 130012； 2.北华大学计算机科学与技术学院，吉林 吉林 132021； 3.东北电力大学电气工程学院，吉林 吉林 132012)

风电是一种输出功率具有随机波动性的电源，分析风电功率波动特性时，采样时间间隔长短的不同会影响对其分析结果的准确性。在众多的采样时间间隔中，期望找到一个采样时间间隔使得分析结果与风电的基本波动特性最为相近，又能缩短工程上的计算分析时间，并将这个采样时间间隔称之为本征时间尺度。首先建立可以刻画风电功率波动特性的指标体系，然后对各指标在不同时间尺度下的变化规律及趋势进行分析，最后在详细探讨采样时间对风电特性的影响后，确定本征时间尺度。

风电功率；波动特性；采样时间间隔；本征时间尺度

Project supported by Jilin Provincial Natural Science Foundation of China(20140101079JC)

0 引言

风能作为一种分布广泛的清洁能源，已受到全世界各国的高度重视。作为风能利用主要形式的风力发电，其发展速度日益加快。风能的间歇性决定了风电功率具有不可精确预期的波动性，这也正是风电并网产生影响的根本所在。

随着大规模风电并网给电力系统安全稳定运行带来影响的日益加大，国内外研究学者对风电功率波动特性进行了深入的研究分析。文献[1-4]通过不同的方法对风电功率进行预测，并对预测精度进行了分析。文献[5-6]设定风速满足威布尔分布，通过风速与风电机组输出功率的关系得到风电功率的分布，进而得出风电功率的波动特性。文献[7]提出可以采用带位移因子与伸缩系数的t分布(t location-scale)来描述风电功率波动特性的概率分布。但是这些文献对风电功率时序波动特性的量化分析研究并不多。

为此，文献[8]在对实测运行数据进行分析的基础上，得到该地区风电限风的时序特征。文献[9]分析了风电场的输出功率概率分布和多个风电场的联合输出功率特性，并给出了其在电力系统分析中的应用。文献[10]分析了不同时间尺度下风电功率波动对电网的影响程度。文献[11]基于中国东北某省级电网千万千瓦级风电基地实测功率数据，定量分析了风电功率波动在不同时间、空间尺度上的分布特性。文献[12]较为全面地综述了国内外短期风电功率预测技术的研究现状，介绍了风电功率预测的相关物理与统计方法，并对预测误差产生的原因及评价方法做了进一步分析。文献[13]对感应发电机输入矩阵的功率波动幅值与电机参数或连接点参数的反向阻抗之间的关系进行了研究，并通过仿真软件对其有效性进行了验证。文献[14]利用双参数Weibull分布对历史的风速数据按月进行拟合，提出基于灰色模型的预测未来年份中对应月的风速分布参数的预测方法。文献[15]利用风速频率瑞利分布对平均风速进行均一化并分析风功率密度，提出了相当风速和有功风功率密度的概念。文献[16]分析了风力机背面风速的计算方法，建立了考虑机组尾流效应的风速模型，并分析了尾流效应对风电场输出特性的影响。文献[17]提出了平抑功率波动的混合储能系统容量优化配置方法，建立了考虑蓄电池寿命损耗的混合储能系统成本模型，并利用某风电场的历史数据验证了该方法的经济优越性。文献[18]利用储能系统来降低风电功率波动对电网的影响。文献[19]提出一种基于功率波动的滤波算法，并将其应用于能量储存系统以验证该算法的有效性。

在风电输出功率波动特性分析的过程中，采样时间间隔的选择对波动特性分析的稳定性有着重要影响，采样时间间隔越短，分析的稳定性越高。因此，在保证风电功率波动特性分析稳定性的基础上，合理地选取采样时间间隔，具有重要的现实意义。本文以某风电基地现场实测运行数据为依据，对多时间尺度下的风电功率波动特性进行分析，得到风电功率随时间尺度变化的趋势及规律，进而确定本征时间尺度。

1 建立风电功率波动特性指标

为研究分析风电场(群)输出功率波动的时间特性，定义如下指标：

1)风电功率平均值。

(1)

2)风电功率最大值。

Pmax=max(Pi),i=1,2,…,n

(2)

3)风电功率标准差。

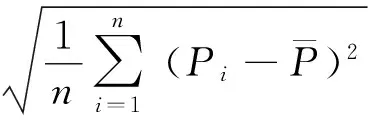
(3)

4)风电功率波动量。

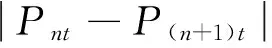
(4)

5)风电功率变化率。

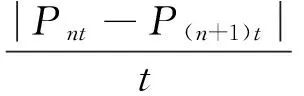
(5)

6)风电功率波动指数。

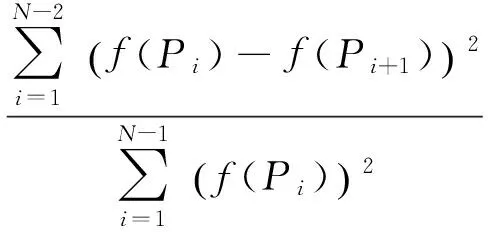
(6)

2 风电场群输出功率波动时间特性分析

为研究风电场群输出功率波动的时间特性，本文以某巨型风电场群2013年全年数据为背景，对风电功率的变化幅度和速率做规律性分析。在分析时，选取不同的采样时间间隔，分别计算对应的风电功率波动量和风电功率波动率及其概率分布，并求取不同采样时间间隔下风电功率波动量和波动率的最大值。采样时间间隔变化跨度包括5、10、30和60 min。

2.1风电场群输出功率波动量随采样时间间隔不同的变化规律

风电场群总体功率波动量的波动曲线、概率分布及其最大值，均随采样时间间隔的变化而变化，具体变化规律如图1—3所示。

图1 风电功率波动量与不同采样时间间隔的关系曲线Fig.1 Relationship curve between wind power fluctuations and different sampling intervals

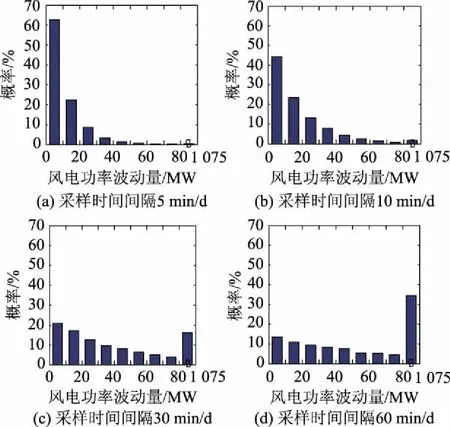
图2 不同采样时间间隔条件下风电功率波动量分布区间示意图Fig.2 Wind power fluctuations distribution diagram under different sampling intervals

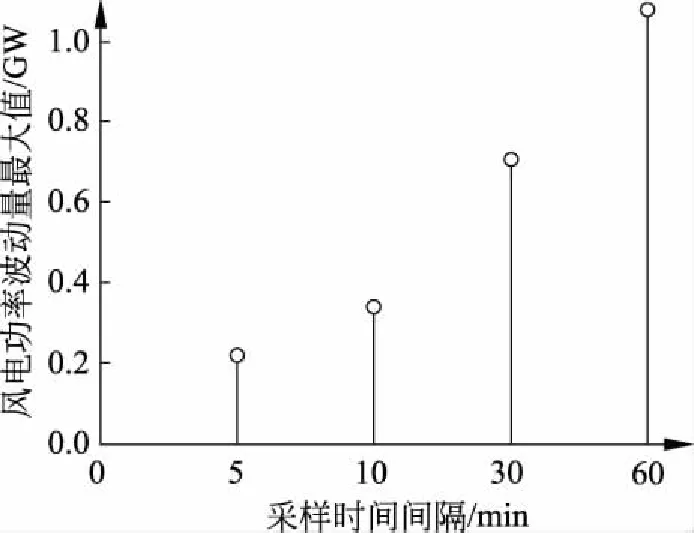
图3 风电功率波动量最大值随采样时间间隔的变化规律Fig.3 Variation law in maximum wind power fluctuation along with sampling intervals

随着采样时间间隔的增大，风电场群输出功率的波动量逐渐增大；风电场群输出功率波动量的瞬时分量在小尺度变化范围内的分布概率逐渐减少，在大尺度变化范围内的分布概率逐渐增大；风电场群输出功率波动量的最大值逐渐增大。

2.2风电场群输出功率波动率随采样时间间隔不同的变化规律

风电场群总体功率波动率的波动曲线、概率分布及其最大值，均随采样时间间隔的变化而变化，具体变化规律如图4—6所示。

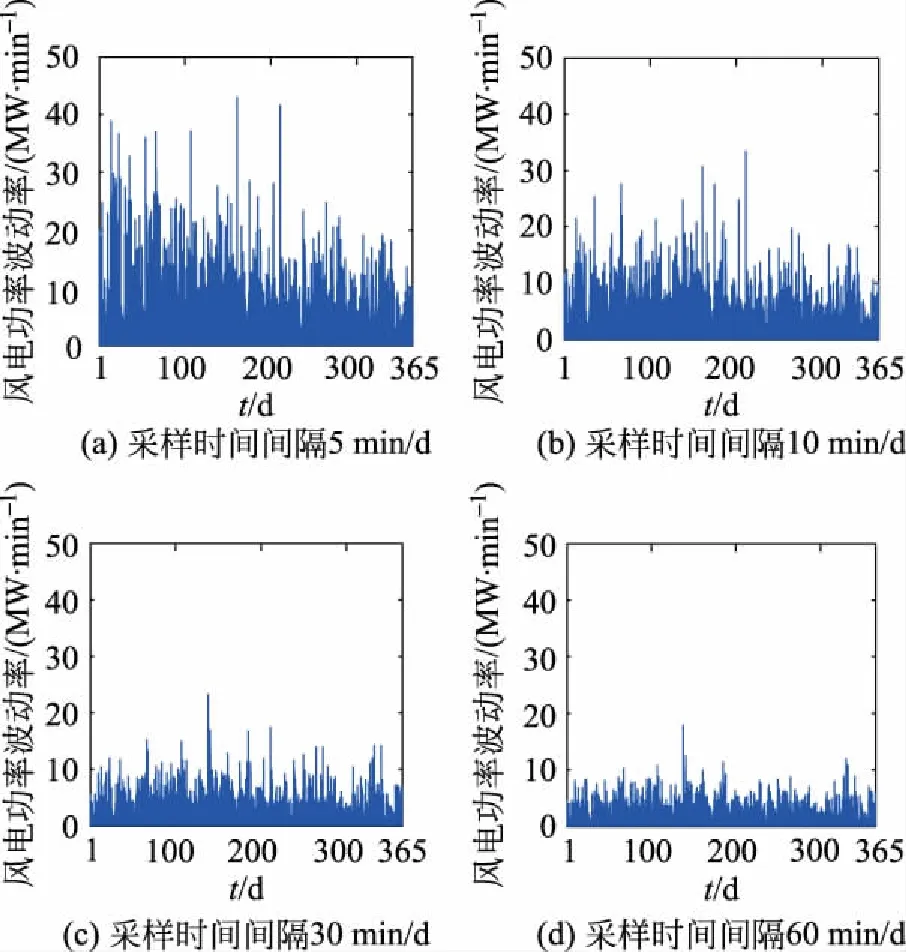
图4 风电功率波动率与不同采样时间间隔的关系曲线Fig.4 Relationship curve between wind power volatilities and different sampling intervals

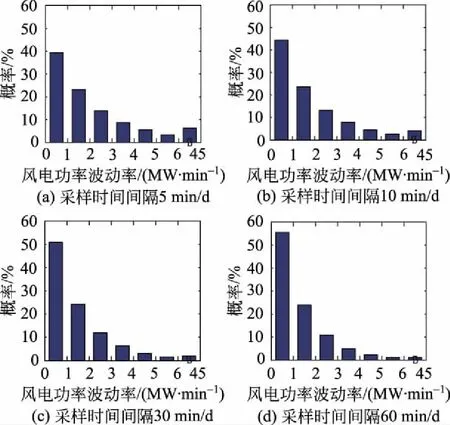
图5 不同采样时间间隔条件下风电功率波动率分布区间示意图Fig.5 Wind power volatilities distribution diagram under different sampling intervals

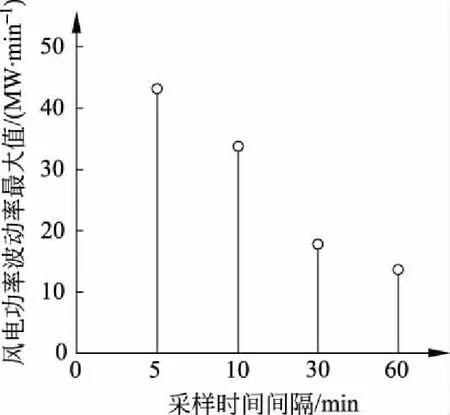
图6 风电功率波动率最大值随采样时间间隔的变化规律Fig.6 Variation law in maximum wind power volatility along with sampling intervals

图7 风电功率平均值与时间尺度的关系图Fig.7 Relation chart between average wind power and time scale

随着采样时间间隔的增大，风电场群输出功率的波动率逐渐减小；风电场群输出功率波动率的瞬时分量在小尺度范围内的分布概率逐渐增大，在大尺度范围内的分布概率逐渐减小；风电场群输出功率波动率的最大值逐渐减小。

3 确定本征时间尺度

3.1风电功率波动特性与时间尺度的关系

为方便观察和比较，风电场的功率是其折算为标么值后的结果。

1)风电功率平均值。

可以反映出所研究风电场群某一时刻或某段时间内输出功率的整体水平，如图7所示：随着时间尺度的增大，风电功率平均值增大，且平均值的波动程度增大，故风电功率平均值的可信度降低。

2)风电功率最大值。

由图8所示的风电功率最大值与时间尺度的关系图中可以看出，随着时间尺度的增大，最大值有所下降。

图8 风电功率最大值与时间尺度的关系图Fig.8 Relation chart between maximum wind power and time scale

3)风电功率标准差。

标准差可以反映所研究风电场群某一时刻或某段时间内输出功率的离散程度，如图9所示：风电功率标准差在小时间尺度上基本持平，但随着时间尺度的增大，标准差也会增大，说明风电功率波动也会随之越来越剧烈。

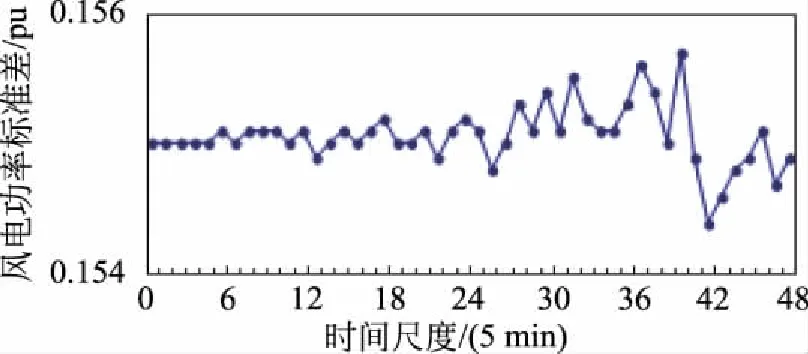
图9 风电功率标准差与时间尺度的关系图Fig.9 Relation chart between standard deviation wind power and time scale

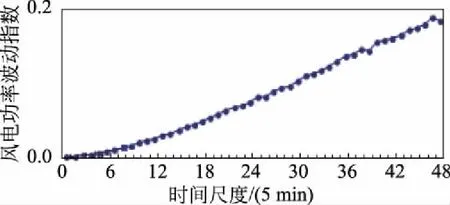
图10 风电功率波动指数与时间尺度的关系图Fig.10 Relation chart between fluctuation index wind power and time scale

4)风电功率波动指数。

本研究采用样地法取样。2017年10月和11月，分别于3类生态系统中顺相同坡向各设置3条样带，每样带内从坡底到坡顶设置3个20 m × 20 m样方。在草地和人工林每样方内的4个拐角和中心取1 m× 1 m的草本样方，在次生林每样方内相同方法分别取5 m× 5 m样方调查灌木和1 m× 1 m样方调查草本。因此，样地共有9个20 m×20 m样方，45个1 m×1 m草本小样方和45个5 m×5 m灌草层小样方。水准仪测量坡度，罗盘测量坡向。

波动指数考虑了时间序列上相邻两点的落差，该指数越大，说明时间序列曲线波动越剧烈；反之，波动指数越小，时间序列曲线波动越平稳。由图10可看出：风电功率波动指数在小时间尺度上几乎趋近于0；并且随着时间尺度的增大，风电功率波动指数增大，风电功率波动越剧烈。

3.2本征时间尺度的确定

在分析风电功率波动特性时，采样时间将直接影响分析结果的准确性;同时，采样时间的长短也会影响工程应用计算的速度。在上述波动指标的基础上，结合熵权法用熵权确定权重，得到一个风电功率综合波动系数为

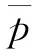
(7)

权系数体现了指标的信息量，熵权值越大表示该指标对综合决策的作用越大，用综合波动指标来刻画风电功率的波动特性会使结果更加客观。如图11所示，风电功率综合指标随时间尺度的增大而增大;但在前30 min内，综合指标变化较小，可忽略不计：故可将30 min作为刻画风电功率波动特性的本征时间尺度。

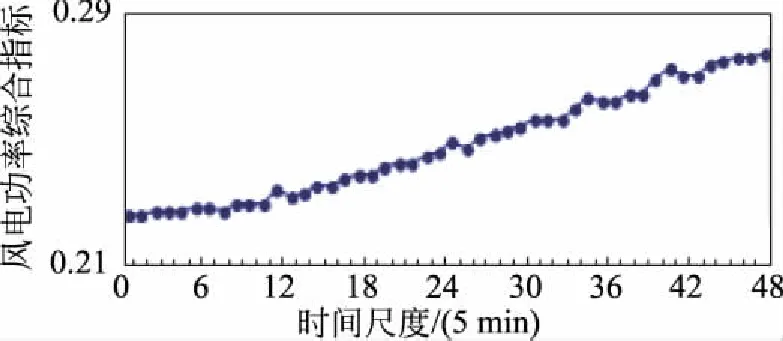
图11 风电功率综合指标与时间尺度的关系图Fig.11 Relation chart between wind power comprehensive index and time scale

3.3风电功率综合指标的偏差校核

由图11可知，随着时间尺度的增大，综合指标值偏离最小采样时间下的值也随之增大。定义偏差值为Δp，计算公式如下：

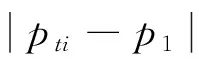
(8)

为体现其偏离标准的程度，将式(8)变形，求其相对误差，得

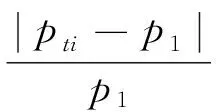
(9)

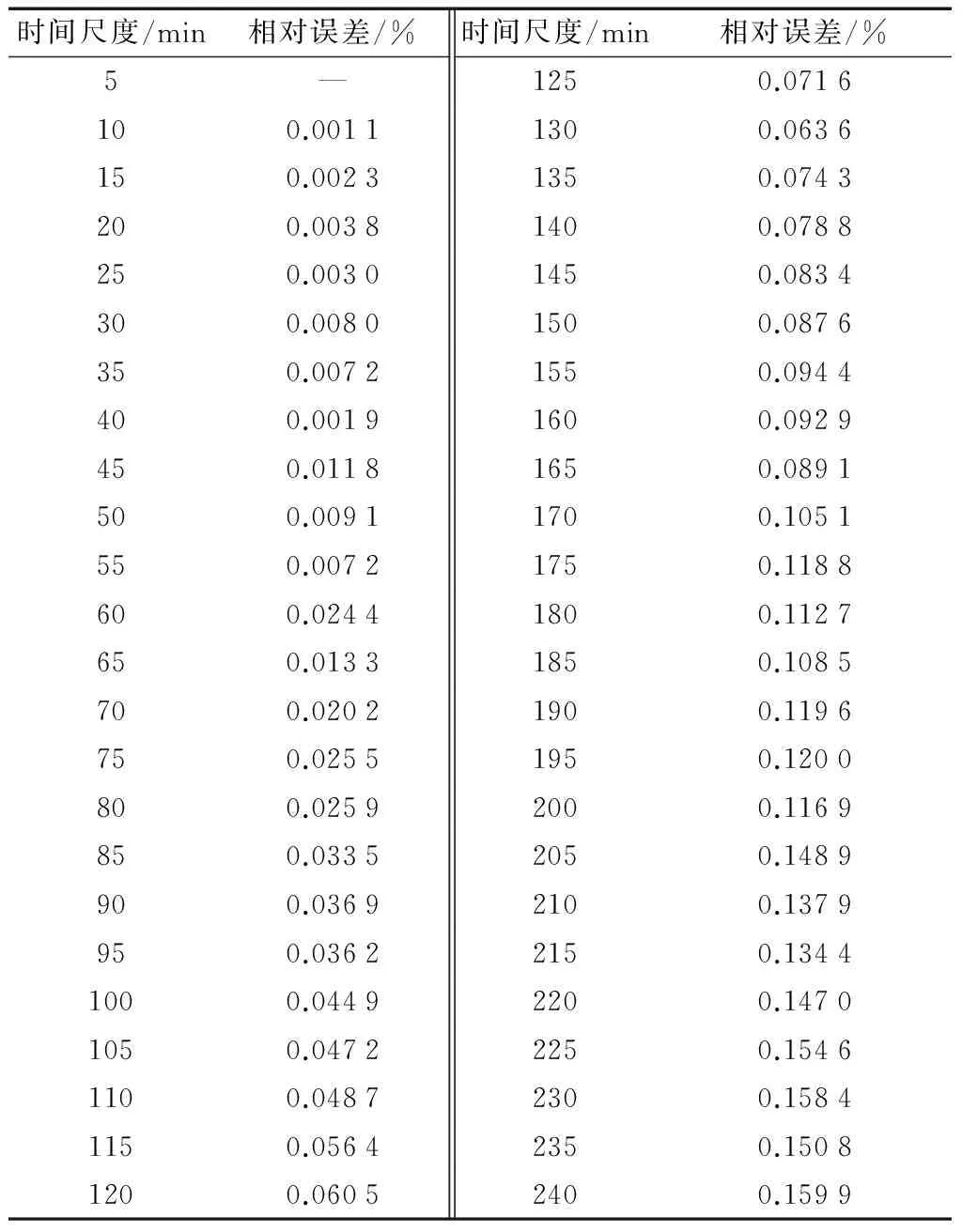
表1 风电功率综合指标相对误差表Table 1 Relative error of integrated wind power indicators

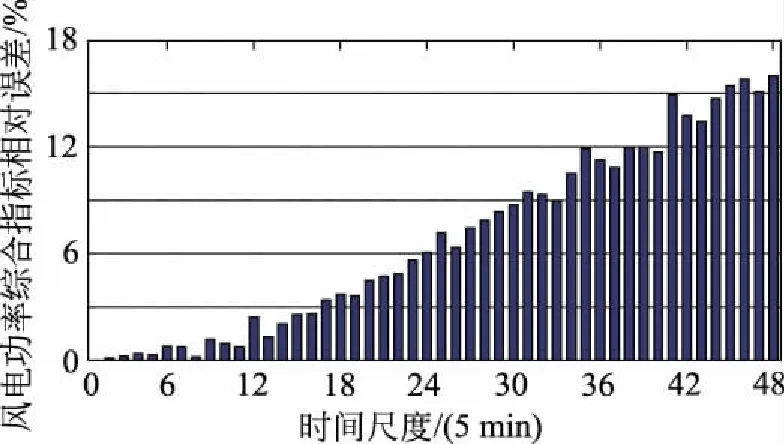
图12 风电功率综合指标相对误差与时间尺度的关系图Fig.12 Relation chart between relative error of integrated wind power indicators and time scale

由表1和图12可看出：风电功率综合波动系数的相对误差在30 min内小于1%，满足电力系统规划的精度要求；与采样时间间隔为5 min相比，其数据量是其1/6倍，计算时间也随之减少，大大提高了工作效率，故可将30 min作为本征时间尺度。

4 结论

本文详细分析了巨型风电场群输出功率波动的时间特性，并在此基础上找到了本征时间尺度。主要研究结论如下：

1)随着采样时间间隔的增大，巨型风电场群风电功率的波动量逐渐增大，且波动量的最大值逐渐增大，波动量的瞬时分量在小尺度变化范围内的分布概率逐渐减小，在大尺度范围内的分布概率逐渐增大。

2)随着采样时间间隔的增大，巨型风电场群风电功率的波动率逐渐减小，且波动率的最大值逐渐减小，波动率的瞬时分量在小尺度范围内的分布概率逐渐增大，在大尺度范围内的分布概率逐渐减小。

3)通过对风电功率平均值、最大值、标准差、波动指数以及综合波动指标的分析，找到了一个既可以提高采样速度，又可以减少采样数据的存储空间，但同时又不会影响风电功率波动固有特性的采样时间尺度，即在电力系统规划问题的研究中，可直接选取30 min为采样时间间隔。

[1] 杨秀媛， 肖洋， 陈树勇. 风电场风速和发电功率预测研究[J]. 中国电机工程学报， 2005, 25(11): 1-5. YANG Xiuyuan， XIAO Yang， CHEN Shuyong． Wind speed and generated power forecasting in wind farm[J]． Proceedings of the CSEE， 2005， 25(11)： 1-5．

[2] 范高锋， 王伟胜， 刘纯， 等. 基于人工神经网络的风电功率短期预测系统[J]. 电网技术， 2008， 32(22)： 72-76. FAN Gaofeng， WANG Weisheng， LIU Chun， et al． Artificial neural network based wind power short term prediction system[J]． Power System Technology， 2008， 32(22)： 72-76．

[3] 杨琦， 张建华， 王向峰， 等. 基于小波-神经网络的风速及风力发电量预测[J]. 电网技术， 2009， 33(17)： 44-48. YANG Qi， ZHANG Jianhua， WANG Xiangfeng， et al． Wind speed and generated wind power forecast based on wavelet-neural network[J]． Power System Technology， 2009， 33(17)： 44-48．

[4] 刘纯， 范高锋， 王伟胜， 等. 风电场输出功率的组合预测模型[J]. 电网技术， 2009， 33(13)： 74-79. LIU Chun， FAN Gaofeng， WANG Weisheng， et al． A combination forecasting model for wind farm output power[J]． Power System Technology， 2009， 33(13)： 74-79． [5] VILLANUEVA D, PAZOS J L, FEIJo A. Probabilistic load flow including wind power generation[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1659-1667.

[6] USAOLA J. Probabilistic load flow with correlated wind power injections[J]. Electric Power Systems Research, 2010, 80(5): 528-536.

[7] 林卫星， 文劲宇， 艾小猛， 等. 风电功率波动特性的概率分布研究[J]. 中国电机工程学报， 2012， 32(1)： 38-46. LIN Weixing， WEN Jinyu， AI Xiaomeng， et al． Probability density function of wind power variations[J]． Proceedings of the CSEE， 2012， 32(1)： 38-46．

[8] 高凯， 朱加明， 葛延峰， 等. 联网风电场集群运行特性分析[J]. 东北电力大学学报， 2014， 34(4)： 11-16. GAO Kai, ZHU Jiaming, GE Yanfeng, et al. Analysis on operating characteristics of clustered wind farms[J]. Journal of Northeast Dianli University, 2014, 34(4): 11-16.

[9] 张义斌， 王伟胜. 风电场输出功率的概率分布及其应用[J]. 电力设备， 2004， 5(8)： 38-40. ZHANG Yibin， WANG Weisheng． Probability distribution of power output for wind power field and its application[J]． Electrical Equipment， 2004， 5(8)： 38-40．

[10] POUL S, NICOLAOS A C. Power fluctuations from large wind farms[J]. IEEE Trans. on Power Systems, 2007, 22(3): 958-965.

[11] 崔杨， 穆钢， 刘玉， 等. 风电功率波动的时空分布特性[J]. 电网技术， 2011， 35(2)： 110-114. CUI Yang， MU Gang， LIU Yu， et al． Spatiotemporal distribution characteristic of wind power fluctuation[J]． Power System Technology， 2011， 35(2)： 110-114．

[12] 谷兴凯， 范高锋， 王晓蓉. 风电功率预测技术综述[J]. 电网技术， 2007， 31(S2)： 335-338. GU Xingkai， FAN Gaofeng， WANG Xiaorong． Summarization of wind power prediction technology[J]． Power System Technology， 2007， 31(S2)： 335-338．

[13] GO T, NORIHIDE K, MASATOSHI M, et al. Study on power fluctuation characteristics of wind energy converters with fluctuating turbine torque[J]. Electrical Engineering in Japan, 2005, 153(4): 1-11.

[14] 丁明， 吴伟， 吴红斌. 风速概率分布参数预测及应用[J]. 电网技术， 2008， 32(32)： 10-14. DING Ming， WU Wei， WU Hongbin． Research on forecasting of probabilistic distribution parameters of wind speed and its

application[J]． Power System Technology， 2008， 32(32)： 10-14．

[15] 杨振斌， 朱瑞兆， 薛桁. 风电场风能资源评价两个新参数： 相当风速、 有功风功率密度[J]. 太阳能学报， 2007， 28(3)： 248-251. YANG Zhenbin， ZHU Ruizhao， XUE Heng． Two new concepts on wind energy assessment in wind farm： equivalent wind speed， available wind power density[J]． Acta Energiae Solaris Sinica， 2007， 28(3)： 248-251．

[16] 曹娜， 赵海翔， 任普春， 等. 风电场动态分析中风速模型的建立及应用[J]. 中国电机工程学报， 2007， 27(36)： 68-72. CAO Na， ZHAO Haixiang， REN Puchun， et al． Establish and application of wind speed model in wind farm dynamic analysis[J]． Proceedings of the CSEE， 2007， 27(36)： 68-72．

[17] 靳雯皓， 刘继春. 平滑风电功率波动的混合储能系统容量优化配置[J]. 分布式能源， 2017， 2(2)： 32-38. JIN Wenhao， LIU Jichun． Capacity optimization configuration of hybrid energy storage system for smoothing wind power fluctuation[J]． Distributed Energy， 2017， 2(2)： 32-38.

[18] MARY B, GORAN S. Value of bulk energy storage for managing wind power fluctuations[J]. IEEE Trans on Energy Conversion, 2007, 22(1): 197-205.

[19] LI Wei, GÉZA J, CHAD A. Attenuation of wind power fluctuations in wind turbine generators using a DC bus capacitor based filtering control scheme[C]//IEEE 4th World Conference on Photovoltaic Energy Conversion. Waikoloa, Hawaii, USA: IEEE, 2006, 1(1): 216-221.

时 彤

(编辑 谷子)

IntrinsicTimeScaleDeterminationBasedonAnalyzingWindPowerOutputFluctuationFeatures

SHI Tong1， JIANG Zhuo2， XIAO Bai3

(1. Datang Northeast Electric Power Test & Research Institute, Changchun 130012, Jilin Province, China; 2. Computer Science and Technology College, Beihua University, Jilin 132021, Jilin Province, China; 3. School of Electrical Engineering,Northeast Electric Power University, Jilin 132012, Jilin Province, China)

Wind power is a kind of power with stochastic volatility output power. Different sampling time lengths may affect the preciseness of analysis results when analyzing the characteristic of wind power fluctuation. We expect to find one sampling time length which can make the analysis result closest to the fundamental volatile features and shorten the computation and analysis time in project, and named this sampling time length as the intrinsic time scale. Firstly, this paper establishes the index system that is able to depict the volatile features of wind power, and then analyzes the change rules and trends of all indexes under different time scales. Finally, this paper discusses the impact of sampling time on the wind power characteristics in detail and determines the intrinsic time scale.

wind power; fluctuation characteristic; sampling time interval; intrinsic time scale

TK 81;TM 71

： A

： 2096-2185(2017)04-0053-06

10.16513/j.cnki.10-1427/tk.2017.04.009

吉林省自然科学基金项目(20140101079JC)

2017-04-05

时 彤(1991—)，女，硕士研究生，从事风电功率波动特性以及电力系统规划方面的研究工作,shitongxtt@163.com；

姜 卓(1978—)，女，硕士，副教授，从事多目标优化算法、图形图像处理等方面的研究工作,abbey1998@sina.com；

肖 白(1973—)，男，博士，教授，长期从事电力系统规划、城市电网风险评估、电力系统继电保护等方面的研究与教学工作,xbxiaobai@126.com。