考虑负荷静态特性的主动配电网多目标调压策略
2017-09-29汤庆峰赵天阳
吴 旭,汤庆峰,赵天阳
(1.国网安徽省电力公司,安徽 合肥 230022; 2.国网冀北电力有限公司经济技术研究院,北京 西城 100045; 3.新能源电力系统国家重点实验室(华北电力大学),北京 昌平 102206)
考虑负荷静态特性的主动配电网多目标调压策略
吴 旭1,汤庆峰2,赵天阳3
(1.国网安徽省电力公司,安徽 合肥 230022; 2.国网冀北电力有限公司经济技术研究院,北京 西城 100045; 3.新能源电力系统国家重点实验室(华北电力大学),北京 昌平 102206)
为消除规模化分布式电源接入给配电网电压造成的不利影响,提出适用于主动配电系统的多目标电压调控策略。计及主动配电系统负荷的静态特性,分析不同负荷特性对主动配电系统运行的影响。进一步地,以分布式电源的有功和并网点电压等为决策对象,计及配电网安全运行约束,构建以清洁能源损失最小、电压偏移最小和网损最小为目标的电压调控模型,并采用改进的并行多目标差分进化算法对模型进行求解。以IEEE-33节点系统为例,验证所提出模型和算法的有效性,并讨论负荷静态特性对电压调控的影响。
主动配电网;分布式电源;调压;多目标差分进化
0 引言
规模化分布式电源(distributed generation,DG)并网改变了传统配电网内的单向潮流分布,将对配电网运行在规划、运行和控制等多方面产生影响,同时也为配电网进行主动运行提供了契机,促使以主动配电网(active distribution network, ADN)为代表的新技术获得广泛关注[1-3]。另外,ADN可通过使用灵活的网络拓扑结构实现对DG进行主动控制和主动管理[4-6]。
研究表明,主动配电网内电压管理的对象已由电容器等无功装置扩展至DG、储能系统等[7-10];调控目标也由单纯的经济性扩展至清洁能源利用等;但忽略了常规负荷的电压响应特性,而负荷的静态特性会改变配电网的网损等[11],影响电压管理的效果;同时,常规电压管理中仅对DG进行定功率因数控制,弱化了逆变器并网型DG的无功调节能力。
因此本文将构建含光伏电站并网的ADN系统及计及负荷静态特性的ADN调压模型。同时,为体现ADN消纳清洁能源和保障用户供电质量的社会职责,在调压模型中以清洁能源利用最大化和电压偏差最小为共同目标。最后,基于多目标差分进化算法(multi-objective differential evolution,MODE)中的子代生成机制,提出并行MODE(parallel MODE,PMODE)算法,以提高模型的求解效率。
1 负荷特性对ADN运行的影响
1.1负荷静态特性
负荷静态特性表述了负荷功率与节点电压和系统频率间的关系,一般采用二次多项式、幂指数两种代数方程描述[12]。配电网内频率可认为恒定,在节点电压变化范围较小时,可采用幂指数的形式进行表述:
式中:Pd,i,Qd,i为节点i有功和无功负荷功率的实际值;Pd0,i,Qd0,i为节点i额定电压时的有功和无功负荷功率值;Ui,U0,i为节点i的实际和额定电压幅值;αi,βi为节点i有功和无功负荷功率的电压特性指数,其参考值如表1所示[13]。

表1 电压特征系数参考值Table 1 Reference values of voltage characteristic coefficient
1.2计及负荷特性的ADN潮流分析方法
光伏经逆变器并网,在不同控制方式下,可等值为PQ节点和PV节点[13]。因DC/AC逆变器可通过控制实现无功出力调节,具有一定的无功调节能力,本文将并网型光伏表述为PV转PQ节点。
在计及负荷静态特性时,ADN内的潮流方程可表述如下:
(3)

为不失一般性,本文采用Newton-Raphson法求解式(3)—(6)表述的潮流方程。
1.3负荷静态特性对ADN的影响
以IEEE-33节点系统为例,表述不同负荷特性对ADN内节点电压和网损的影响。ADN内含有3个并网型光伏电站,其有功出力、电压设定值和无功出力上、下限如表2所示。
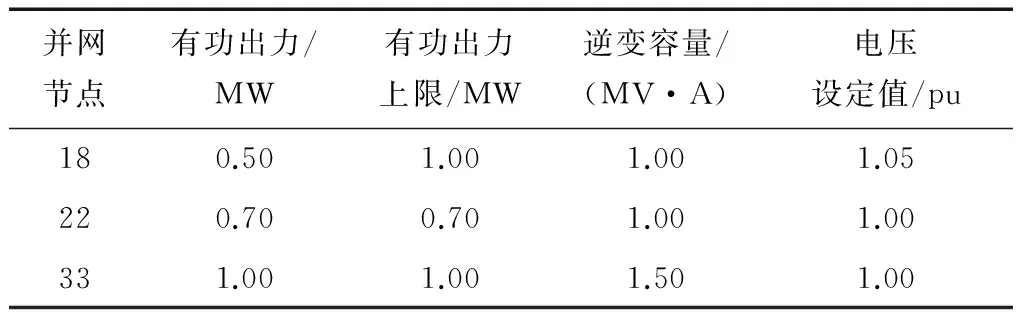
表2 并网光伏电站参数Table 2 Parameters of grid-connected PV power station
分别设定各节点负荷为居民负荷、商业负荷和工业负荷,其典型参数见表1。以恒功率负荷各节点电压幅值为基准,不同负荷特性下各节点的电压幅值差值如图1所示。

图1 不同负荷特性下各节点的电压幅值Fig.1 Node voltage amplitude under different load characteristics
如图1所示,在光伏电站出力相同的情况下,负荷的电压特性将改变各节点的电压幅值;且由于工业负荷的无功功率-电压灵敏度最高,使得工业负荷下各节点的电压幅值最高。同时,系统内的网损由0.055 0 MW下降至0.052 8、0.052 4和0.052 4 MW。可见,不同的负荷特性对ADN的运行产生了安全和经济性的影响。
2 ADN多目标调压模型
2.1目标函数
含光伏并网的ADN不仅要保障系统的安全运行,还需要充分利用清洁能源,改善ADN的供电质量,并实现ADN的经济运行,分别阐述如下:
1)弃光量最小。
(7)
式中:PDGmax,i为DGi的最大有功出力;PDG,i为DGi的实际有功出力;NPV为ADN内并网光伏电站的数量。
2)电压偏差最小。
(8)
式中NB为ADN内节点的数量。
3)网损最小。
(9)
式中:Ploss为网损;P0为馈线始端的有功功率。
2.2约束条件
1)光伏出力限制。
光伏的最大有功出力PDGmax与光照强度、温度等相关,在ADN不能消纳过多的光伏出力时,可通过更改逆变器的直轴电流等降低光伏电站的有功出力[14],即出现弃光:
0≤PDG,i≤PDGmax,i
(10)
由于光伏发电系统中的逆变器逆变容量有限,从而限制光伏发电系统的无功调节能力:

(11)
式中SDG,i为光伏发电系统逆变器的逆变容量。
2)支路潮流限制。
大量的光伏接入,有可能造成ADN出现线路阻塞等情况,因此需限制各支路潮流在一定范围内:
(12)
式中:Sij为支路ij的始端实在功率;Smaxij为支路ij始端实在功率上限;Pij为支路ij的始端有功功率;Qij为支路ij的始端无功功率;Gij和Bij为支路ij的电导和电纳值;θij为支路ij的始端、末端攻角差。
3)节点电压限制。
在电压超出一定范围时,将引起DG保护装置的动作;同时,由于本文计及了负荷的电压响应特性,如果电压超出一定范围,将引起负荷功率剧烈变化;因此,需限定各节点电压幅值在一定范围内:
Umin,i≤Ui≤Umax,i
(13)
式中Umin,i和Umax,i为节点i电压幅值的下限和上限。
4)关口功率约束。
为抑制规模化分布式电源并网后ADN对外部电网的影响,需限定ADN根节点处与外网的功率交换在一定范围内:
(14)
式中:P0min、P0max和Q0min、Q0max分别为关口有功功率交换下限、上限和无功功率交换下限和上限。
5)功率平衡约束。
(15)
综上可知,ADN多目标调压模型的调控对象为PV节点的有功和基点电压、关口处的电压,包含功率平衡等非线性非凸约束,同时追求清洁能源利用、供电质量和经济性的优化,为典型的非线性多目标优化问题(nonlinear multi-objective optimization problem,NMOP)。
3 并行差分进化算法
在基于差分进化(differential evolution,DE)的MODE中,选择策略可分为:将子代个体和父代个体直接混合获得混合种群的PDDE和将子代个体和父代个体进行选择操作后获得混合种群的DEMO[15-17]。因PDDE具有更好的全局搜索能力,本文选用PDDE作为ADN内的调压模型的求解算法,以为决策者提供更好的方案。
因PDDE求解的问题为无约束问题,本文采用文献[18]中提出的基于目标函数修正的约束处理方法处理ADN调压模型中的众多约束,从而形成了PMODE算法。采用并行计算的PMODE计算流程如图2所示。

图2 并行多目标差分进化计算流程Fig.2 Flow chart of PMODE
4 算例分析
4.1算例描述
本文基于IEEE-33节点系统对所提出的模型和算法进行测试。IEEE-33节点系统的负荷为3.715 0 MW,各节点电压幅值下限、上限和基准都设定为0.95、1.05和1.00 pu,关口处交换有功功率和无功功率下限、上限为:0、5 MW和-1、2 Mvar。假设ADN内各节点负荷都为工业负荷,其他参数详见文献[19]。ADN内含有3个并网型光伏电站,其参数见表2。
在PMODE的突变和交叉操作中,控制参数F和CR分别影响算法的搜索步长和子代个体对父代个体的继承能力,从而影响算法的性能。在先验知识较少的情况下,可将控制参数内嵌入个体,伴随种群进化而进行参数自适应控制[19]。
式中:r1、r2、r3、r4为[0,1]之间的均匀分布随机数;τ1、τ2分别为种群中调整个体相对应的F和CR的概率。本文中Fmin、Fmax、τ1、τ2分别取定值0.1、0.9、0.1和0.1,文献[19]中的测试表明Fmin、Fmax、τ1、τ2的变化并不会显著改变算法的寻优结果。
PMODE中种群规模设定为70,最大迭代次数设为100。并行计算的计算平台为Matlab 2013b,Intel Core i7-3770@3.4GHz处理器,8 G RAM。
4.2结果分析
4.2.1 模型有效性验证
以ADN内所有节点负荷都是功率型负荷为基准,并以负荷类型为工业负荷和商业负荷作对比,获得的Pareto前沿如图3所示,各极端解如表3所示。

图3 不同负荷特性下的Pareto前沿Fig.3 Pareto-front under different load characteristics

负荷特性弃光量/(MW·h)节点电压偏移量/pu网损/(MW·h)恒功率负荷0.00010.00210.05340.73690.00070.04580.66260.05540.0335工业负荷(α=0.18,β=6.00)0.00050.00690.05270.79760.00070.04480.63970.04510.0330商业负荷(α=0.99,β=3.15)0.00010.00150.05020.78430.00070.04540.65180.00130.0354
由图3和表3可知,在计及负荷静态特性时,系统的网损和电压偏移指标发生了较大变化:获得的弃光量近似一致时,节点电压偏移量由0.002 1增加至0.006 9,而网损则由0.053 4 MW·h下降为0.052 7 MW·h;同时,工业负荷下获得的最优网损方案优于恒功率负荷下获得的方案。
进一步地,由表3可知,在所有负荷都为商业负荷时,所获得的最优弃光方案优于工业和恒功率下所获方案;同时,在所有负荷都为商业负荷时,最优网损方案的节点电压偏移量显著优于其他两种负荷特性下的最优网损方案。
4.2.2 算法有效性分析
在Matlab本地并行计算模式下,开启不同的计算内核,完成PMODE的计算所需时间如图4所示。可见,随着内核数量的增加,相同计算时间所需时间近似呈线性下降。

图4 不同数量内核计算所需时间Fig.4 Computation time required by different numbers of computer kernels
5 结论
针对含光伏并网的ADN系统,本文计及负荷的电压响应特性,构建了以光伏有功出力、并网点电压、平衡节点电压为控制对象,以充分利用清洁能源和电压管控效果为共同目标的调压策略;并采用基于并行适应值评估的多目标差分进化算法求解ADN调压模型。
测试结果表明:不同的负荷特性都对ADN的调压决策产生了显著影响;与不计及负荷特性相比,在以最优弃光和最优网损为目标时,计及负荷特性更有助于ADN运行人员做出更贴合实际的决策方案;同时,开启内核的数量对并行计算所需时间也产生了显著影响(即随着内核数量的增加,计算时间近似呈线性趋势下降)。
[1] ZENG M, DUAN J, WANG L, et al. Orderly grid connection of renewable energy generation in China: management mode, existing problems and solutions[J]. Renewable and Sustainable Energy Reviews, 2015(41): 14-28.
[2] 刘念, 张清鑫, 李小芳. 基于核函数极限学习机的分布式光伏短期功率预测[J]. 农业工程学报, 2014, 30(4): 152-159. LIU Nian, ZHANG Qingxin, LI Xiaofang. Distributed photovoltaic short-term power output forecasting based on extreme learning machine with kernel[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(4): 152-159.
[3] AI Q, WANG X, HE X. The impact of large-scale distributed generation on power grid and microgrids[J]. Renewable Energy, 2014(62): 417-423.
[5] JUNG J, ONEN A, RUSSELL K, et al. Local steady-state and quasi steady-state impact studies of high photovoltaic generation penetration in power distribution circuits[J]. Renewable and Sustainable Energy Reviews, 2015(43): 569-583.
[6] TREBOLLE D, HALLBERG P, LORENZ G, et al. Active distribution system management[C]//22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Beijing, 2013.
[7] 赵波, 王财胜, 周金辉, 等. 主动配电网现状与未来发展[J]. 电力系统自动化, 2014, 38(18): 125-135. ZHAO Bo, WANG Caisheng, ZHOU Jinhu, et al. Present and future development trend of active distribution network[J]. Automation of Electric Power Systems, 2014, 38(18): 125-135.
[8] GABASH A, LI P. Active-reactive optimal power flow in distribution networks with embedded generation and battery storage[J]. IEEE Transactions on Power Systems, 2012, 27(4): 2026-2035.
[9] VALVERDE G, VAN CUTSEM T. Model predictive control of voltages in active distribution networks[J]. IEEE Transactions on Smart Grid, 2013, 4(4): 2152-2161.
[10] 刘一兵, 吴文传, 张伯明, 等. 基于有功-无功协调优化的主动配电网过电压预防控制方法[J]. 电力系统自动化, 2014, 38(9): 184-191. LIU Yibing, WU Wenchuan, ZHANG Boming, et al. Overvoltage preventive control method based on active and reactive power coordinated optimization in active distribution network[J]. Automation of Electric Power Systems, 2014, 38(9): 184-191.
[11] 李安, 曹杰, 许彬, 等. 计及静态负荷模型的配电网重构[J]. 武汉大学学报: 工学版, 2014, 47(6): 810-815. LI An, CAO Jie, XU Bin, et al. Distribution networks reconfiguration considering static load model[J]. Engineering Journal of Wuhan University, 2014, 47(6): 810-815.
[12] TAYLOR C W. Power system voltage stability[M]. New York, USA: McGraw-Hill, 1994. [13] 朱星阳, 张建华, 刘文霞, 等. 考虑负荷电压静特性的含分布式电源的配电网潮流计算[J]. 电网技术, 2012, 36(2): 217-223. ZHU Xingyang, ZHANG Jianhua, LIU Wenxia, et al. Power flow calculation of distribution system with distributed generation considering static load characteristics[J]. Power System Technology, 2012, 36(2): 217-223.
[14] CAGNANO A, DE TUGLIE E, LISERRE M, et al. Online optimal reactive power control strategy of PV inverters[J]. IEEE Transactions on Industrial Electronics, 2011, 58(10): 4549-4558.
[15] MUSRRAT A, PATRICK S, MILLIE P. An efficient differential evolution based algorithm for solving multi-objectiveoptimization problems[J]. European Journal of Operational Research, 2012(217): 404-416.
[16] 徐昆. 群智能算法及其并行计算技术的研究与应用[D]. 济南: 山东大学, 2014. XU Kun. Research and application of swarm intelligence algorithm and parallel computation technology[D]. Jinan: Shandong University, 2014.
[17] BREST J, GREINER S, BoKOVIB, et al. Self-adapting
control parameters in differential evolution: a comparative study on numerical benchmark problems[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(6): 646-65
[18] 刘文霞, 赵天阳, 邱威, 等. 基于闭环供应链的集中性充- 换电系统运营优化[J]. 中国电机工程学报, 2014, 34(22): 3732-3742. LIU Wenxia, ZHAO Tianyang, QIU Wei, et al. Operation optimization of centralized battery swap charging system based on closed-loop supply chain[J]. Proceedings of the CSEE, 2014, 34(22): 3732-3742.
[19] KAMH M Z, IRAVANI R. A sequence frame-based distributed slack bus model for energy management of active distribution networks[J]. IEEE Transactions on Smart Grid, 2012, 3(2): 828-836.

吴 旭
(编辑 谷子)
Multi-ObjectiveVoltageRegulationMethodforActiveDistributionNetworkConsideringLoadStaticCharacteristics
WU Xu1, TANG Qingfeng2, ZHAO Tianyang3
(1. State Grid Anhui Electric Power Company, Hefei 230022, Anhui Province, China; 2. State Grid Jibei Electric Power Economic Research Institute, Xicheng District, Beijing 100045, China; 3. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Changping District, Beijing 102206, China)
To mitigate the adverse effects of large-scale distributed generation on the voltage of distribution network, this paper proposes a multi-objective voltage control method under the active distribution scheme. With considering the load static characteristics of active distribution system, this paper analyzes the impact of load characteristics on the active distribution system operation. Further, this paper constructs the voltage control model to minimize the clean energy curtailment, the voltage profile derivation, and the active power losses, with taking the active power output of distribution generation and grid-connected voltage as decision-making object and considering the distribution network security operation constraint. Then, this paper uses the improved parallel multi-objective differential evolution algorithm to solve the model. Base on the simulation carried out on the modified IEEE-33 bus test system, the effectiveness of the proposed model and algorithm is demonstrated, and the impact of load static characteristics on the voltage regulation is discussed.
active distribution network; distribution generation; voltage regulation; multi-objective differential evolution
TK 01; TM 71
: A
: 2096-2185(2017)04-0047-06
10.16513/j.cnki.10-1427/tk.2017.04.008
2017-02-02
吴 旭(1984—),男,博士,工程师,从事电力系统调度运行工作,wuxu_spy@163.com;
汤庆峰(1988—),男,博士研究生,从事配网规划与优化调度工作;
赵天阳(1989—),男,博士研究生,研究方向为电力系统优化运行、博弈论。
