基于改进模拟退火遗传算法的梯级水电站长期优化调度
2017-09-29范金骥
范金骥
(中国大唐集团科学技术研究院有限公司华东分公司,安徽 合肥 230000)
基于改进模拟退火遗传算法的梯级水电站长期优化调度
范金骥
(中国大唐集团科学技术研究院有限公司华东分公司,安徽 合肥 230000)
在使用传统优化方法处理梯级电站数量庞大的长期优化调度时会出现“维数灾”及寻优效果差等问题。研究工作利用遗传算法进行计算,并对其进行了利于计算的改进,将自适应的控制理论加入交叉和变异算子,让其根据适应度的值自动改变,生成初始群体时使用混沌理论,并引入模拟退火方法,将两者的优点结合起来,生成了改进模拟退火遗传算法,提升了全局寻优能力和局部搜索能力,避免了算法陷入局部最优解。将改进后的算法程序应用于建立的模型中,通过与常规遗传算法的比较与分析,结果表明改进模拟退火遗传算法全局搜索能力强、求解效果好,为解决梯级水电站长期优化调度提供了新方法。
梯级水电站;长期优化调度;遗传算法;混沌算法;模拟退火
0 引言
小水电作为国际公认的清洁可再生能源,是一种重要的分布式能源,适宜在贫困山区农村发展以及分散开发,具有明显的社会公益性。整个流域的经济收益最大化是水电运行的重要指标,一个流域梯级水电站长期优化调度主要的目标是让整个梯级水电站的负荷分配与发电用水协调作用。通常是以水文预报作为基础,根据水文径流预报数据,利用优化算法结合目标函数建立水库长期优化调度模型,实现水库的最优调度。但在实际计算时因为流域中有复杂的来水与水利联系,各级流域间上级电站的实际发电用水和泄水量会影响下游流域各电站的用水分配,使得梯级水电站的长期优化调度成为一个难以处理的问题。相关学者利用传统动态规划法具有计算限制少、适合多阶段优化处理的特点,在实际应用中取得了不错的效果[1-2], 但对于水电站数量较多的大型流域,计算时会出现“维数灾”的难题。为此,遗传算法、神经网络法[3]、粒子群算法和蚁群算法等拥有全局优化能力和较强的鲁棒性、通用性的算法,在梯级水电站长期优化调度的应用中得到了广泛的应用。有些学者针对遗传算法局部搜索能力弱的特点进行了改进[4]。传统遗传算法可直接对求解对象计算,不受优化问题是否可求导、是否连续等因素的限制,还能多点出发搜索最优解[5]。国内外的研究人员把改进后的传统遗传算法用在了水库长期优化调度中,取得了一些成果[6],但也会存在局部搜索能力弱、计算时间较长等缺点,需要进一步的改进和优化。研究工作中试图把改进后的传统遗传算法用到梯级水电站长期优化调度问题中,但发现在进化后期还是会出现搜索效率较低,导致“早熟现象”的发生。为此,对遗传算法进行了改进:(1)利用混沌的方法生成初始群体,可以更有效的使初始解均匀的分布于解的空间中,降低了算法会陷入局部最优的可能性[7]。(2)将自适应的方法用于遗传算法中的交叉和变异算子[8],让算法拥有更高的效率和较强的鲁棒性。(3)综合模拟退火的特点,形成改进模拟退火遗传算法[9]。该算法的根本目的是发挥遗传算法较强全局搜索能力的同时,利用模拟退火算法局部搜索能力强的优点,在进化寻优的过程中更有效地获得最优解。这样,2种算法都可以克服本身存在的缺点,有利于提升算法的寻优效果以及进化末期的收敛精度。
1 梯级水电站长期优化调度模型的建立
梯级水电站长期优化调度根据不同的准则会有多种建模方法。主要有以下3种模型:(1)梯级发电量最大模型;(2)发电效益最大模型;(3)最大化最小出力模型[10]。不同的优化模型,其目标函数也有较大的差别。根据实际的生产调度需求,本文使用梯级发电量最大模型作为判定标准。考虑到计算的有效性,在确定型优化调度和随机优化调度模型中使用前者。确定型优化模型中的目标函数是指调度期内各电站的入库流量已知,综合水量平衡、水库库容、水位约束、下泄流量等各种约束条件的情况下,同时考虑到航运、灌溉、防洪等因素后制定的优化调度过程。当有N座水库串联,计算时间段按月划分,梯级水电站总发电量最大的目标函数可表示为下面的式子:
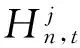
其约束条件包括:
(1)水量平衡约束
Vn,t+1=Vn,t+(Qn,t-qn,t-dn,t)Δt
(4)
(2)水库库容约束
(5)
(3)发电量约束
(6)
(4)水电站处理约束
(7)
(5)出库流量约束
(6)上、下游水库之间的水力联系
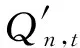
(10)
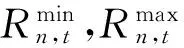
2 改进模拟退火遗传算法
在进行遗传算法的运算时,由于算法设计的缺陷和实际数据的误差,会出现算法早熟与局部最优解等情况,导致遗传算法的计算结果和计算效率达不到预期的水平。为此,使用混沌的方法得到初始种群,在遗传算法中的交叉和变异算子加入自适应的策略,融合模拟退火算法中局部搜索能力强的特点,提出了改进模拟退火遗传算法。
2.1混沌算法初始化种群
针对计算时容易陷入局部最优的情况,利用混沌算法生成梯级水电站优化调度问题中的初始群体。混沌并不是完全的混乱状态,而是大量出现在非线性优化系统中的有着多变的内在结构的一类存在形式。此处采用 Logistic 映射的混沌特性公式:
yn+1=∂yn(1-yn)
(11)
式中:∂为控制变量,取值范围为[0,4];yn为自变量x第n次的计算值,取值范围为[0,1]上的随机数[12]。公式中,初始取值x1=0.06,n=500的混沌动态映射图如图1所示,试验证明,Logistic映射是维持群体多样性的有效方法。
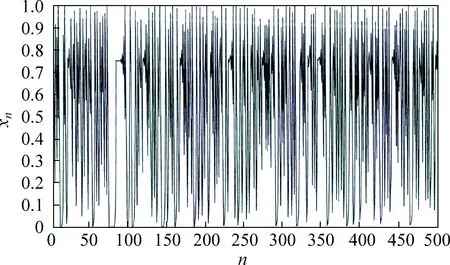
图1 混沌动态映射图Fig.1 Chaotic dynamic map
计算过程中,由于混沌变量具有遍历特点,将混沌变量从混沌空间映射到解空间时,可以更有效地使问题的初始解均匀分布于解的空间中,以此方法形成的初始群体降低了计算时会陷入局部最优解的可能性[13]。
2.2遗传算法中遗传算子的改进
针对遗传算法中的选择、交叉、变异操作做了以下2点改进:
(1)利用“轮盘赌选择法”时可能会出现早熟收敛的情况。改进后将群体按照适应度的值降序进行排序,将排序出的个体等分成4份,直接淘汰适应度值最后1/4的个体,适应度排在中间2/4的个体直接复制到下一代,剩余的适应度排序最高的前1/4个体数量加倍。下一代的群体数量总和与初始时相同。改进后的选择操作可以直接过滤适应度最差的一部分个体,快速的增加了群体中优良适应度的个体数量,提升了算法的收敛速度。
(2)为了让算法拥有更高的效率和较强的鲁棒性,采用自适应函数来调节交叉算子pc和变异算子pm。将自适应的计算方法引入计算可以使交叉概率pc和变异概率pm随着群体适应度的变化而变化,便于得到最佳的操作因子。
在算法中使用的自适应函数为:
式中:控制参数pc1,pc2,pm1,pm2取值范围是(0,1);f′为进行交叉的2个个体中适度较大的值;f为当前个体的适应度;fmax和favg分别为进化群体中最大的适应度值和群体的平均适应度。经过仿真实验发现,当pc1=0.8,pc2=0.5,pm1=0.1,pm2=0.01时,在大部分计算实例中可以得到较好的计算效果。当然在应用于具体的算例时还需根据实际情况对参数作相应的调整[14]。
由上式可以发现,当(fmax-favg)的值变小时,此时算法基本收敛到了局部最优的情况,应该加大pc和pm的值,使得计算过程脱离局部最优的情况。说明此参数表示了算法的收敛程度。式子(f′-favg)和(fmax-f)的值是个体性状好坏的标准。当个体中较大的适应度值低于种群的平均适应度或在种群中适应度的最大值远大于现在个体的适应度时,说明此时群体中个体的表现性状不是很好,此时需要使用较大的pc和pm的值。相反就需要减小pc和pm的值以保持现有的群体中好的个体不因为频繁的交叉和变异而被破坏。
2.3改进模拟退火遗传算法的流程
改进后的遗传算法,结合模拟退火算法后就可以形成一种新的混合遗传算法。这种运算方式是根据混沌的方法产生1个初始群体,通过改进后的选择、自适应交叉和变异等操作产生1个新的群体,如此循环迭代,当群体中最优个体的值不如父代的最优个体时,选出最优个体,继续进入模拟退火算法循环,满足约束条件后结束整个过程。改进后的模拟退火遗传进化算法既体现了遗传算法具有较强的全局搜索能力,又利用了模拟退火算法较强的局部搜索能力。
本文提出的算法具体流程如下:
(1)初始化相关计算参数,如交叉概率pc1,pc2,变异概率pm1,pm2,进化的最大代数T,种群的规模M,初始温度t,结束温度t′,降温系数x等。
(2)利用混沌算法对群体进行初始化,形成初始的染色体S。
(3)分别计算群体中各个个体的适应度值f(i),记录下最优个体的适应度值fmax。
(4)种群选择操作。按照上述选择方法,筛选出进入新群体的个体。
(5)种群交叉、变异操作。根据式(12)(13)计算出交叉和变异概率后进行相应操作。
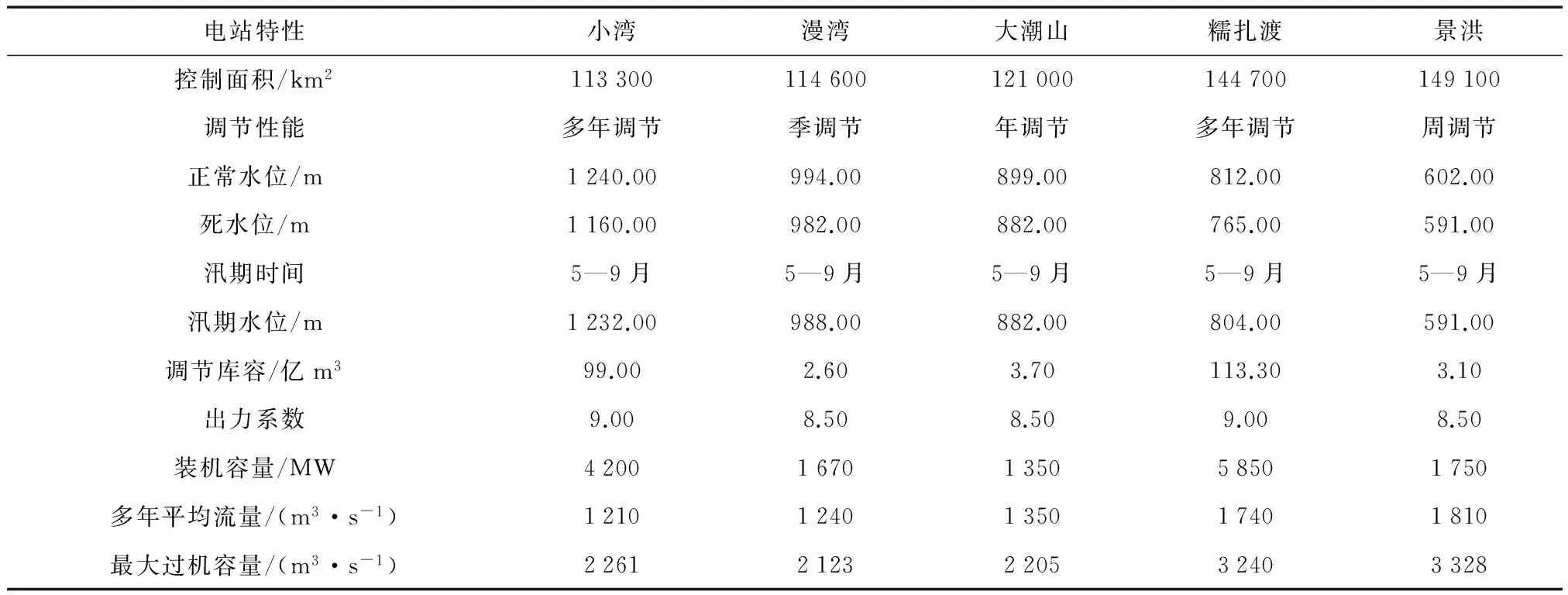
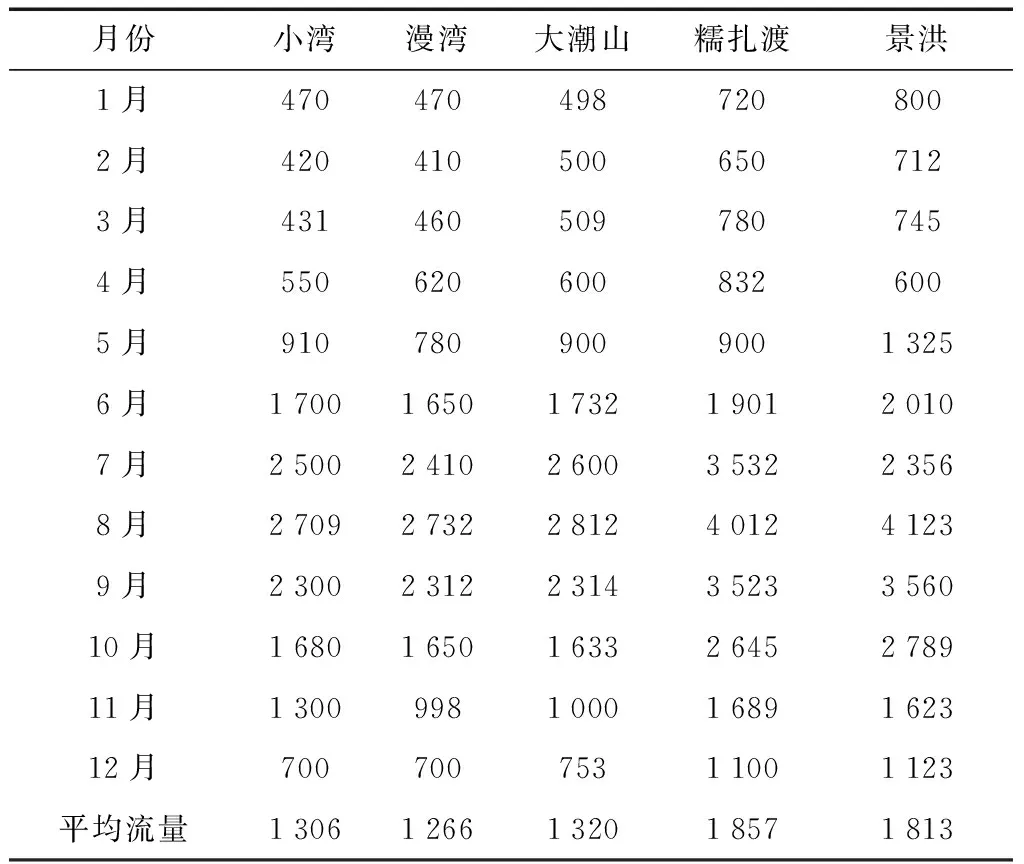
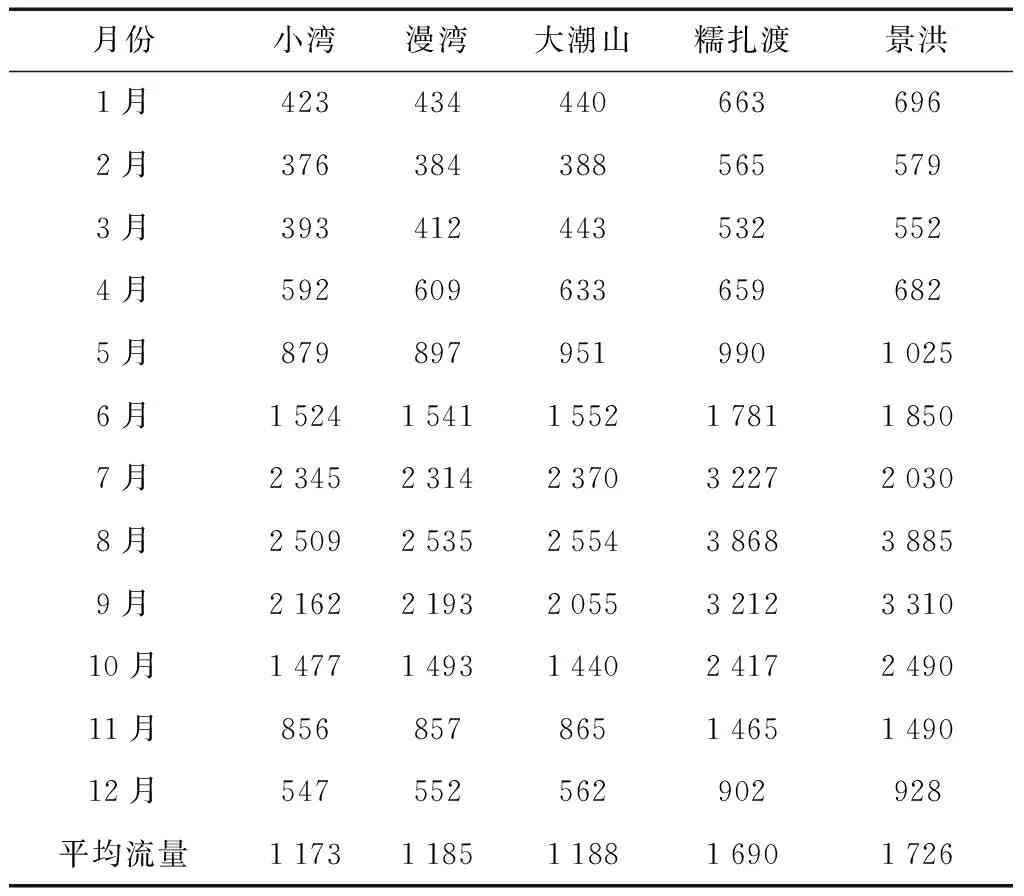
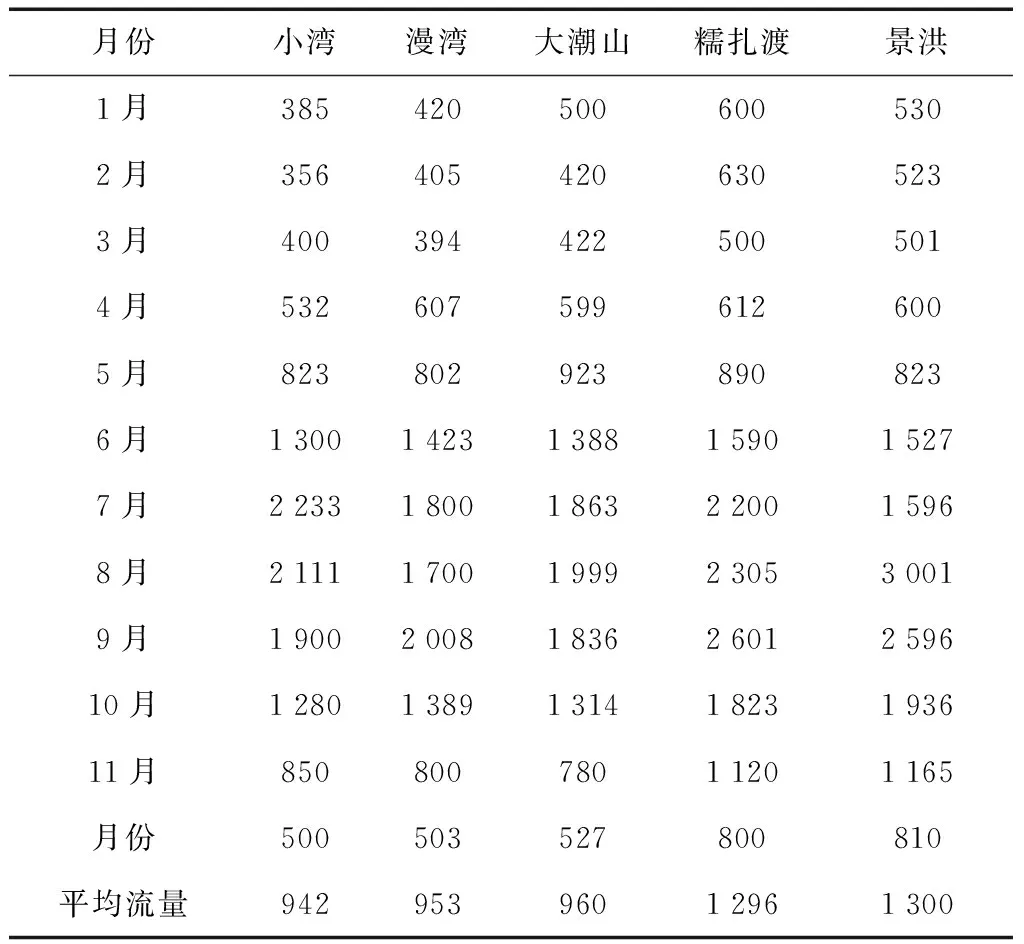
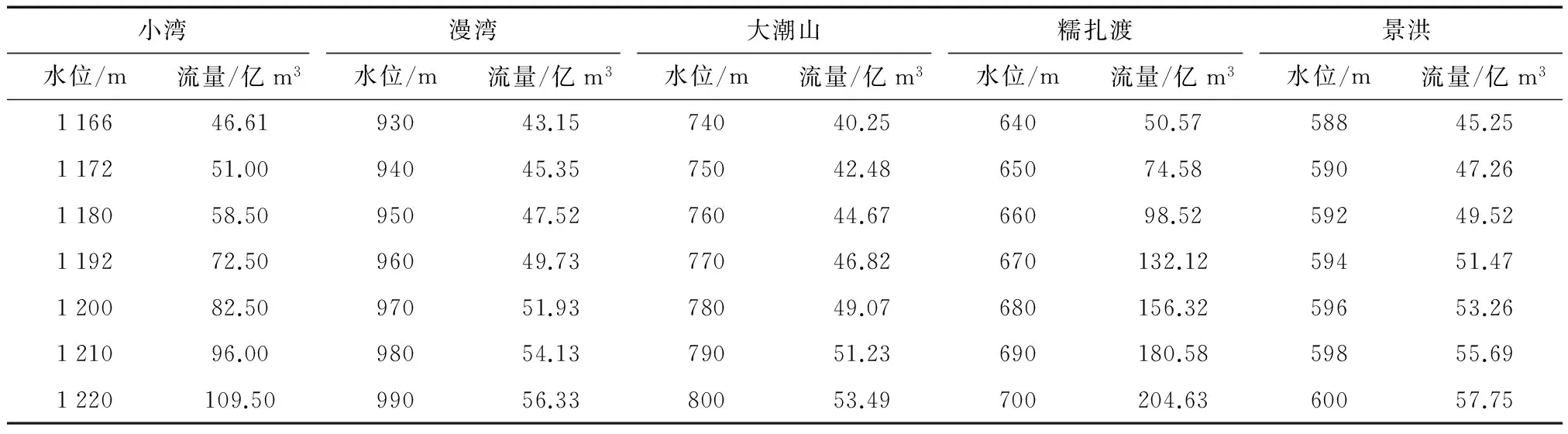
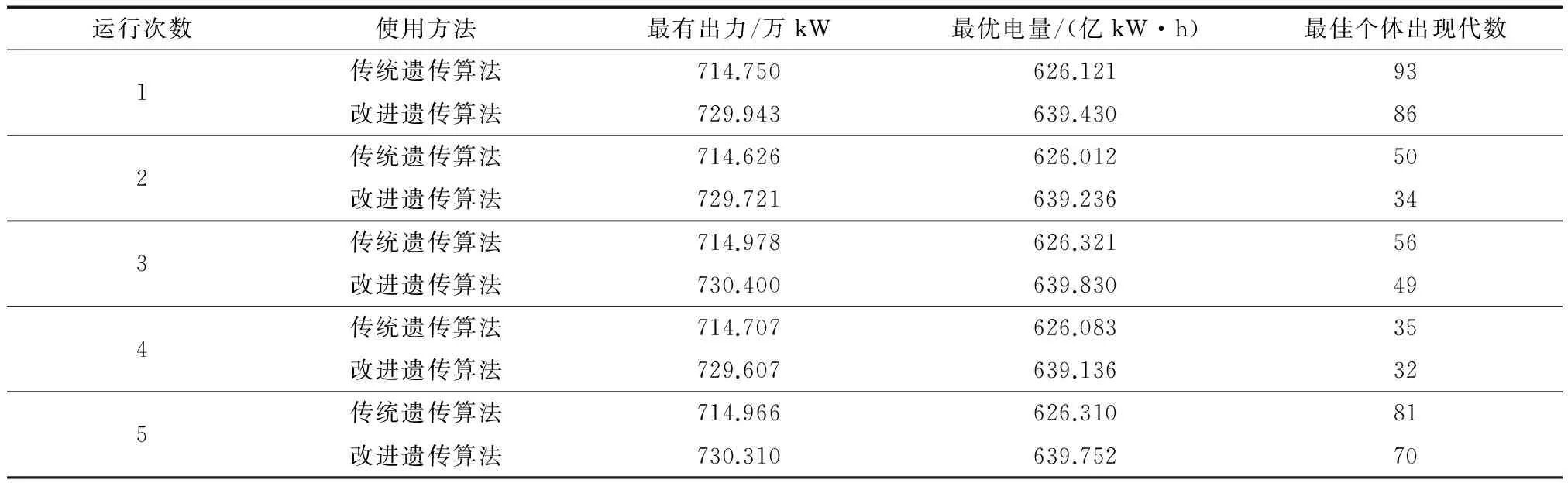
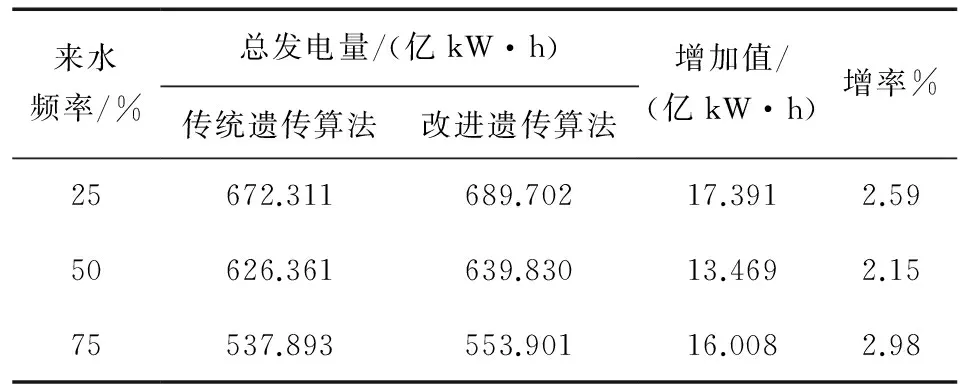
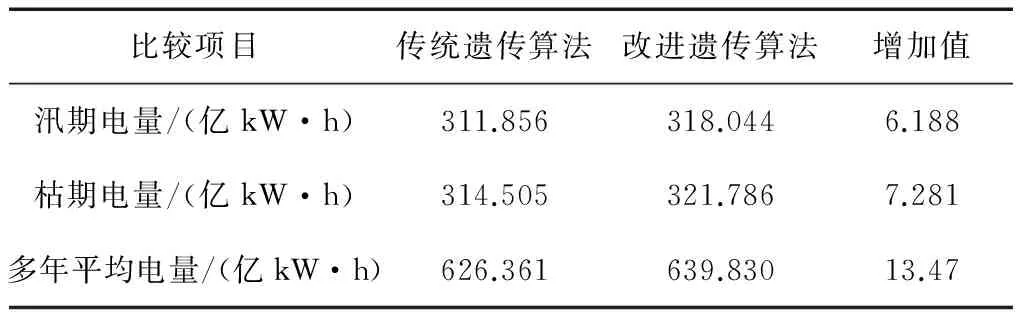
(6) 将最好个体的适应度值f′(i)与fmax进行判断,若f′(i)≥fmax,遗传代数Ngen=Ngen+1;继续进行上述遗传算法的循环,当f′(i) (7)计算得到通过遗传算法计算之后的全局最优个体。 (8)进入模拟退火算法的循环,上一个步骤计算出的最优的染色体与设定的模拟退火参数都带入其中: 1)通过操作产生新的群体B′。 2)算出算法的增量Δt′=C(B′)-C(B),其中 C(B)为一种评价群体好坏的标准。 3)当Δt′<0时,将新的种群B′作为新的最优解,相反,以概率exp(-Δt′/t)把新的群体B′作为解。 4)当满足算法终止条件时,跳出循环并输出当前解为群体最优解,程序运行结束。否则,接着进行模拟退火的循环。 5)温度t逐渐降低,(t=t*x),且t>0,接着进行步骤 1)继续算法。 以澜沧江下游小湾到景洪5个具有较好调节能力的水电站作为研究对象,测试提出的改进遗传算法的可行性及存在的问题。各水库之间存在区间入流,每个水电站的计算特征值见表1。 3.1算法的计算条件 在进行本文的计算时,条件如下:(1)计算的时段设置为月,调度期设为1年(12个时段);(2)各电站的死水位定为水位下限,正常高水位定为水位上限(汛期时则设定为汛限水位);(3)各电站的出力下限设0,上限是装机容量;(4)各电站的出库下限设0,上限是最大出库流量;(5)各电站始末水位是设定好的值,设定值见下表2。 测试径流釆用频率为25%(丰水年)、50%(平水年)以及75%(枯水年)的典型年入库径流过程,计算过程中釆用面积法求出各电站区间流量。各电站丰水年、平水年以及枯水年的入库流量分别见表3—5。 表1 澜沧江下游梯级水电站群电站特征属性值Table 1 Power station characteristic value of cascade hydropower stations in lower Lancang River 表2 各级电站始末水位设置Table 2 Water level setting at all levels of power stations 表3 各级电站丰水年入库径流过程Table 3 Run in process of all levels of power stations inwet years m3/s 表4 各级电站平水年入库径流过程Table 4 Run in process of all levels of power stations innormal years m3/s 梯级电站的水位库容关系如表6所示。 3.2编码方式 考虑到研究对象较为复杂,为方便求解选用的编码方法为:将时段t时的水库水位等分为n份,按照从小到大的顺序排列,表示为:1,2,3…,n+1。 表5 各电站枯水年入库径流过程Table 5 Run in process of all levels of power stations indry years m3/s 种群中个体的基因值代表了当前水库水位的真实值,每个时段都会有不同的水位值,将所有时段内的数据按照给定顺序放入一个数组中,就形成了群体的初始染色体。时段t的水位可表示为 (14) 式中:zt,max,zt,min分别表示时段t水库水位的最大值和最小值;Nrand为一个小于n的随机数,服从(0,n)的均匀分布;n在算法中的作用是控制计算精度[15]。 3.3约束条件和适应度函数的处理 根据建立的函数模型和水库调度规律,约束条件的处理方式为:水库的出库流量最大值和最小值通过水量平衡方程的计算,直接得到水库水位的最小值和最大值约束;某一时段水库库容约束与出库流量约束得到的水位范围值取交集,得到此时水位的取值范围,计算处理时使用搜索空间限定法,这样既能提升遗传算法的搜索效率,又能让搜索空间中的群体与解空间中的可行解一一对应;在处理电站出力限制时,算完水流出力后,再使用电站的出力限制曲线,进行电站出力的校核和修正;处理保证出力的约束条件时使用罚函数的方法进行计算,把不满足约束条件的个体加以一个惩罚函数,让其适应度的值减小,使其进入下一代群体的概率降低;进行适应度函数计算时采用变量惩罚函数的方法,通过反复试验确定合适的惩罚系数。变量惩罚函数的表达式为 表6 水库水位库容关系表Table 6 Relationship between reservoir water level and storage capacity (15) 式中:F(X)为处理后个体适应度函数;f(X)为原目标函数;m为不满足约束条件的变量总数;λi为惩罚系数;Vi为超越约束条件的量[16-17]。 3.4计算结果分析 计算参数设置如下。传统遗传算法:种群数量m=50,最大进化代数d=100,交叉概率pc=0.7,交叉概率pm=0.01。 改进后的遗传算法:种群数量m=50,最大进化代数d=100,pc1=0.8,pc2=0.5,pm1=0.1,pm2=0.01,初始温度T0=100,按照算法给出的降温公式减到终止温度。 在算法中首先进行上述初始参数的设置,利用Matlab软件,结合编写的算法程序将有关水库特性的水库水位值、水位库容关系、水位流量关系、水轮机的保证出力等条件带入算法进行计算。考虑到每次计算的结果可能出现不同的情况,本文对平水年,丰水年和枯水年分别进行了5次改进遗传算法和基本遗传算法的计算,计算结果见表7。 下面以平水年的优化计算为例,5次不同的计算结果见表8。 表7 最优结果的遗传算法不同来水频率下水电站群优化结果统计Table 7 Optimal results of hydropower station group under different water frequency in genetic algorithm 表8 平水年传统遗传算法与改进遗传算法的5五次运行结果表Table 8 Five running results of conventional genetic algorithm and improved genetic algorithm in normal years 经过计算得到不同算法的梯级流域效益指标对比见表9—10。 表9 改进遗传算法与传统遗传算法的效益指标对比Table 9 Benefit index comparison between improved geneticalgorithm and conventional genetic algorithm 表10 平水年改进遗传算法与传统遗传算法效益分析表Table 10 Benefit analysis of improved genetic algorithm andconventional genetic algorithm in normal years 由上各表显示的数据可知: (1)无论在丰水年、平水年还是枯水年,改进后的遗传算法计算出的每个水电站的发电量和总发电量都要优于传统遗传算法,证明改进后的遗传算法具有良好的优化效果。丰水年和枯水年计算耗时比平水年要长一些,这是因为丰水年在计算时需要对水库弃水作频繁的计算,而计算枯水年发电量时要保证系统的最小出力。改进后的模拟退火遗传算法采用了整体退火选择,在遗传算法之后增加了一个循环,算法中需要父代和子代共同竞争产生新的群体,故计算时间大于基本遗传算法,但这并不影响整体的计算效果。 (2)改进后的遗传算法收敛速度更快,最优解出现的代数早于传统遗传算法。5次计算结果关于最优解的标准差为0.107亿 kW·h,在最优解的比例中占比很小,仅为0.017%。这证明了改进后的算法具有稳定且有效的搜索能力。 (3)改进后的遗传算法将丰水年时多余的水量进行了更好的利用,在枯水年时尽量利用水库的蓄水能力和调节能力增加发电量。由此可以看出,改进模拟退火遗传算法有效地保持了种群的多样性,提高了全局搜索能力,克服了标准遗传算法易早熟和陷入局部最优的缺点。 (4)自然状态下梯级水电站受到降水不均的影响,枯汛期的发电量分配差距较大,改进后降低了汛期发电在全年发电中的比例,表现出梯级水库的调节补偿、蓄丰补枯的特点,大大提高了下游各梯级电站的保证出力和年发电量,提高了流域各梯级的电能质量。 图2给出了2种智能算法的进化过程与梯级水电站调度的发电量对比图。将混沌原理加入遗传算法,初始种群的最大适应度优于标准遗传算法得到的种群。虽然加入了模拟退火算法使得算法的整体计算时间有所加长,但是改进后的遗传算法比基本遗传算法拥有更好的收敛速度,在进化中更早的得到了最优解。 图2 梯级水电站调度的发电量对比图Fig.2 Power generation capacity comparison of cascade hydropower stations (1)改进后的遗传算法计算出的每个水电站的发电量和总发电量都要优于传统遗传算法,具有良好的优化效果。 (2)改进后的遗传算法收敛速度更快,最优解出现的代数早于传统遗传算法,其标准差为0.107亿kW·h,仅占最优解的0.017%,表明算法具有稳定且有效的搜索能力。 (3)改进后的遗传算法将丰水年时多余的水量进行了更好的利用,增加发电量梯级电站的总发电量比基本遗传算法有所提高。 (4)改进后降低了汛期发电在全年发电中的比例,表现出梯级水库的调节补偿、蓄丰补枯的特点,大大提高了下游各梯级电站的保证出力和年发电量,提高了流域各梯级的电能质量证。由此可见改进后的算法为梯级水电站长期优化调度提供了新方法。 由于研究深度和工作经验的限制,本计算方法需要从以下2个方面进行完善: (1)本文在计算时使用的确定型模型,若想把具体的水文情况及来水的预报信息加入到算法中,用于解决梯级水电站长期优化调度过程中的入库径流情况,仍需要进一步研究。 (2)本文计算了5座具有代表性的梯级水电站优化调度的研究并分析了计算结果,并未将澜沧江流域所有电站都进行可行性的计算。如何把算法用于更多的水电站及其计算的收敛性及效果如何还需要进一步的验证。 [1] 李安强, 张建云, 仲志余, 等. 长江流域上游控制性水库群联合防洪调度研究[J]. 水利学报, 2013, 44(1): 59-66. LI Anqiang, ZHANG Jianyun, ZHONG Zhiyu, et al. Study on joint flood control operation for leading reservoirs in the upper Changjiang River[J]. Journal of Hydraulic Engineering, 2013, 44(1): 59-66. [2] 王文川, 雷冠军, 尹航, 等. 基于群居蜘蛛优化算法的水库防洪优化调度模型及应用[J]. 水电能源科学, 2015, 33(4): 48-51. WANG Wenchuan, LEI Guanjun, YIN Hang, et al. Optimal dispatch model of reservoir flood control based on SSO algorithm[J]. International Journal Hydroelectric Energy, 2015, 33(4): 48-51. [3] 刘宇, 钟平安, 张梦然, 等. 水库优化调度ANN模型隐层节点数经验公式比较[J]. 水力发电, 2013, 39(5): 65-68. LIU Yu, ZHONG Ping’an, ZHANG Mengran, et al. Empirical formulae comparison for number selection of hidden layer’s nodes in ANN model applied for reservoir optimal operation[J]. Water Power, 2013, 39(5): 65-68. [4] 周章贵, 董国锋. 合同能源管理——小水电增容改造项目融资新模式[J]. 小水电, 2009(4): 32-36. ZHOU Zhanggui, DONG Guofeng. Energy performance contracting——A new mode of financing in SHP renovation project[J]. Small Hydro Power, 2009(4): 32-36. [5] 周艳聪, 刘艳柳, 顾军华. 小生境自适应遗传模拟退火智能组卷策略研究[J]. 小型微型计算机系统, 2011, 32(2): 323-327. ZHOU Yancong, LIU Yanliu, GU Junhua. Research on test paper auto-generating based on niche adaptive genetic simulated annealing algorithms[J]. Journal of Chinese Computer Systems, 2011, 32(2): 323-327. [6] 游进军, 纪昌明, 付湘. 基于遗传算法的多目标问题求解方法[J]. 水利学报, 2003, 34(7): 64-69. YOU Jinjun, JI Changing, FU Xiang. New method for solving multi objective problem based on genetic algorithm[J]. Journal of Hydraulic Engineering, 2003, 34(7): 64-69. [7] 袁晓辉, 袁艳斌, 王乘, 等. 一种新型的自适应混沌遗传算法[J]. 电子学报, 2006, 34(4): 708-712. YUAN Xiaohui, YUAN Yanbin, WANG Cheng, et al. A novel self-adaptive chaotic genetic algorithm[J]. Acta Electronica Sinica, 2006, 34(4): 708-712. [8] 邬峰, 黄丽亚. 自适应模拟退火遗传算法的改进与应用[J]. 微型机与应用, 2010, 29(9): 84-86. WU Feng, HUANG Liya. Improvement and application of an adaptive simulated annealing genetic algorithm[J]. Microcomputer & its Applications, 2010, 29(9): 84-86. [9] 李文武, 吴稀西, 黄进, 等. 基于随机动态规划的混合式抽水蓄能电站水库中长期优化调度研究[J]. 电力系统保护与控制, 2013, 41(9): 86-93. LI Wenwu, WU Xixi, HUANG Jin, et al. Mid-long term optimization of reservoir operation for hybrid pumped storage power station based on stochastic dynamic programming[J]. Relay, 2013, 41(9): 86-93. [10] 陈明, 张靠社. 基于改进布谷鸟算法的风光储联合供电系统储能容量优化配置研究[J]. 电网与水力发电进展, 2016(8): 141-146. CHEN Ming, ZHANG Kaoshe. Study on optimal storage capacity of energy storage capacity based on improved cuckoo algorithm[J]. Progress in Grid and Hydroelectric Power Generation, 2016(8): 141-146. [11] 郑立刚, 周昊, 王春林, 等. 变尺度混沌蚁群算法在NOx排放优化中的应用[J]. 中国电机工程学报, 2008, 28(11): 18-23. ZHENG Ligang, ZHOU Hao, WANG Chunlin, et al. Application of scaleable chaotic ant colony algorithm in Nox emissions optimization[J]. Proceedings of the CSEE, 2008, 28(11): 18-23. [12] 王涛, 王焕. 改进的自适应混沌差分进化算法[J]. 计算机系统应用, 2013, 22(2): 138-141. WANG Tao, WANG Huan. Improved adaptive chaotic differential evolution algorithm[J]. Computer Systems & Applications, 2013, 22(2): 138-141. [13] 申建建, 程春田, 廖胜利,等. 基于模拟退火的粒子群算法在水电站水库优化调度中的应用[J]. 水力发电学报, 2009, 28(3): 10-15. SHEN Jianjian, CHENG Chuntia, LIAO Shengli, et al. Optimization of hydropower station operation by using particle swarm algorithm based on simulated annealing[J]. Journal of Hydroelectric Engineering, 2009, 28(3): 10-15. [14] 傅蓉, 王维庆, 何桂雄. 基于气象因子的BP神经网络风电场风速预测[J]. 可再生能源, 2009, 27(5): 86-89. FU Rong, WANG Weiqing, HE Guixiong. The forecasting of wind speed in wind farm based on the meteorological factors with BP neural network[J]. Renewable Energy, 2009, 27(5): 86-89. [15] 乔海娟, 张丛林, 张军, 等. 推进我国小水电发展的思考[J]. 海河水利, 2015(2): 35-37. QIAO Haijuan, ZHANG Conglin, ZHANG Jun, et al. Analysis on promoting the development of small hydropower in China[J]. Haihe Water Resources, 2015(2): 35-37. [16] 吴学文, 索丽生, 王志坚. 水电站水库优化调度的改进混沌遗传算法[J]. 水利水电科技进展, 2010, 30(2): 53-57. WU Xuewen, SUO Lisheng, WANG Zhijian. Improved chaotic genetic algorithm for optimal operation of hydropower reservoirs[J]. Advances in Science and Technology of Water Resources, 2010, 30(2): 53-57. [17] 李可, 马孝义, 符少华. 基于改进遗传算法的水电站优化调度模型与算法[J]. 水力发电, 2010, 36(1): 92-96. LI Ke, MA Xiaoyi, FU Shaohua. Scheduling optimization model and algorithm based on improved genetic arithmetic for hydropower station[J]. Water Power, 2010, 36(1): 92-96. 范金骥 (编辑 蒋毅恒) Long-TermOptimalSchedulingofCascadeHydropowerStationsBasedonImprovedSimulatedAnnealingGeneticAlgorithm FAN Jinji (East China Branch, China Datang Corporation Science and Technology Research Institute Co., Ltd., Hefei 230000, Anhui Province, China) Conventional optimization methods have ‘dimension disaster’ problems and poor search efficiencies in solving the long-term scheduling optimization problem of large-scale cascade hydropower stations. In order to achieve better results, the genetic algorithm has been improved in this study. The adaptive control theory is applied to the crossover and mutation operators, such that they can be automatically changed according to the fitness value. Chaos theory is used to generate the initial population, and the simulated annealing method is also introduced. An improved simulated annealing genetic algorithm is proposed by combining the advantages of these two algorithms, which can enhance global optimization capabilities and local search capabilities, and reduce the probability of stuck on local optima. The improved algorithm is then applied to an established model. Through compared with the conventional genetic algorithms, the results show that the improved simulated annealing genetic algorithm has strong global search ability and good solution effect, which can be served as a reference for solving the long-term scheduling optimization problem of large-scale cascade hydropower stations. cascaded hydropower stations; long-term optimal dispatching; genetic algorithm; chaos algorithm; simulated annealing TK 71 : A : 2096-2185(2017)04-0020-09 10.16513/j.cnki.10-1427/tk.2017.04.004 2017-05-09 范金骥(1990—),男,硕士,助理工程师,研究方向为水利能源发电控制系统建模仿真及优化,1003478006@qq.com。3 实例研究

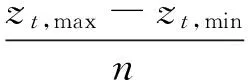


4 结论

