双圆盘的Bergman空间上k阶斜Toeplitz算子的交换性

刘朝美,高娇娇

( 大连交通大学 理学院，辽宁 大连 116028)*

双圆盘的Bergman空间上k阶斜Toeplitz算子的交换性

刘朝美,高娇娇

( 大连交通大学 理学院，辽宁 大连 116028)*

对双圆盘的Bergman空间上k阶斜Toeplitz算子的交换性展开了研究，得到了以共轭解析函数为符号的k阶斜Toeplitz算子可交换的充要条件是其符号函数线性相关.

双圆盘；Bergman空间；斜Toeplitz算子；交换性

0 引言

斜Toeplitz算子是函数空间上的一类算子.1996年，Mark引进了Hardy空间上斜Toeplitz算子的概念[1]，介绍了该类算子的背景，讨论了该类算子的若干性质,并对该类算子的谱等性质展开了深入的讨论[2- 4].Arora 和Batra通过对斜Toeplitz算子定义的推广，得到k阶斜Toeplitz算子的概念，并对该类算子的性质展开了一系列的讨论[5- 8].2004年，安恒斌和蹇人宜将斜Toeplitz算子的定义推广到了单位圆盘的Bergman空间上，并对该类算子的有界性、紧性等性质展开了研究[8].既然可以将Hardy空间上的斜Toeplitz算子推广为k阶斜Toeplitz算子，那么人们自然会想到将Bergman空间上斜Toeplitz算子的概念进行推广. 2007年, Yang、Leng和Lu给出了Bergman空间上k阶斜Toeplitz算子的概念，并对该类算子的谱、交换性等性质展开了研究[9]. 此后，人们又对该类算子的交换性、有界性等性质展开了研究，得到了一些结论[10- 11]. 2012年,朱洪敏给出了多圆盘的Bergman空间上k阶斜Toeplitz算子的概念并对该类算子的交换性、谱、紧性等性质进行了研究[12].

对函数空间上斜Toeplitz算子的性质进行研究时，人们总是希望能够将该类算子的性质由其符号函数给出刻画.本文对双圆盘的Bergman空间上k阶斜Toeplitz算子的性质展开了研究，得到了以共轭解析函数为符号的k阶斜Toeplitz算子可交换的充要条件是其符号函数线性相关.

1 基本概念

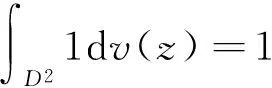
设k≥2是固定的整数, 定义在A2(D2)上的算子Wk[12]为

设φ∈L∞(D2),A2(D2)空间上以函数φ为符号的k阶斜Toeplitz算子Bφ=WkTφ定义为Bφ=WkTφ, 其中Tφ是A2(D2)上以函数φ为符号的Toeplitz算子, 而且以本性有界函数为符号的k阶斜Toeplitz算子均是有界线性算子[12].

2 斜Toeplitz算子的交换性

对A2(D2)空间上以共轭解析函数为符号的k阶斜Toeplitz算子的交换性展开讨论，得到以下结论.

证明 若φ与ψ是线性相关的, 那么显然可得BφBψ=BψBφ.

理性从启示、哲学从信仰中剥离出来并获得独立的形态，并不意味着宗教的消除，正如卡西尔所言：“启蒙运动最强有力的精神力量不在于它摒弃信仰，而在于它宣告的新信仰形式，在于它包含的新宗教形式。”［16］125－126在启示与理性、信仰与哲学的博弈中，“宗教信念应该像任何别的命题一样接受检验——由理性证据来检验”［17］26。启蒙扬弃了宗教的外在形式，形成了新的宗教形态——知性宗教。

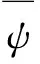
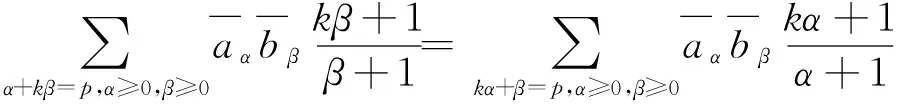
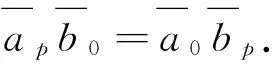
当0≤p=(p1,p2)≤(k-1,2k-1)且p2≥k时, 由等式(2)可得

当0≤p=(p1,p2)≤(2k-1,k-1)且p1≥k时,由等式(2)可得

当0≤p=(p1,p2)≤(2k-1,2k-1)且p1≥k,p2≥k时, 由等式(2)可得

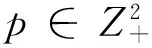
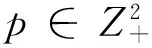
当0≤p=(p1,p2)≤((n+1)k-1,(n+1)k-1)且p1≥nk或p2≥nk时, 由等式(2)可得

[1]MARK C HO.Properties of slant Toeplitz operators[J].Indiana Univ.Math.J.,1996,45(3):843- 862.

[2]MARK C HO.Spectra of slant Toeplitz operators with continuous symbol[J].Michigan Mathematical Journal,1997,44(1):157- 166.

[3]MARK C HO.Adjoints of slant Toeplitz operators[J].Integral Equations and Operator Theory,1997,29(3):301- 312.

[4]MARK C HO.Adjoints of slant Toeplitz operators II[J].Integral Equations and Operator Theory,2001,41(2):179- 188.

[5]ARORA S C,BATRA R.On generalized slant Toeplitz operators[J] .Indian J.Math.,2003,45(2):121- 134.

[6]ARORA S C,BATRA R.On generalized slant Toeplitz operators with continuous symbols[J].Yokohama Mathematical Journal,2004(51):1- 9.

[7]ARORA S C,BATRA R.Generalized slant Toeplitz operators on H2[J].Math.Nachr.,2005,278(4):347- 355.

[8]安恒斌,蹇人宜.Bergman空间上的斜Toeplitz算子[J].数学学报,2004,47(1)：103- 110.

[9]JUN YANG,AIPING LENG,YUFENG LU.K-order slant Toeplitz operators on the Bergman Space[J].Northeast.Math.J.,2007,23(5):403- 412.

[10]YUFENG LU,CHAOMEI LIU,JUN YANG.Commutativity of kth-order Slant Toeplitz operators[J].Mathematische Nachrichten,2010,283(3):1304- 1313.

[11]CHAOMEI LIU,YUFENG LU.Product and Commutativity of kth-order Slant Toeplitz Operators[J].Abstract and Applied Analysis,2013,45(2):900- 914.

[12] 朱洪敏.单位多圆盘上Bergman空间上的k阶斜Toeplitz算子的一些研究[D].上海：华东师范大学,2012.

Commutativity ofk-Order Slant Toeplitz Operators on Bergman Space of Bidisk

LIU Chaomei,GAO Jiaojiao

(School of Mathematics and Physics,Dalian Jiaotong University,Dalian 116028,China)

In this paper,the commutativity ofk-order slant Toeplitz operator on the Bergman space of bidisk are discussed.The necessary and sufficient condition is obtained.For the commutativity ofk-order slant Toeplitz operators with co-analytic symbols,their symbol function are linearly dependent.

bidisk;bergman space;k-order slant Toeplitz operators;commutativity

1673- 9590(2017)05- 0115- 04

A

2016- 07- 30

国家自然科学基金资助项目(11301046)

刘朝美(1980-), 女，副教授,博士， 主要从事函数空间及其算子理论的研究 E-mail:lcm@djtu.edu.cn.