基于云模型和故障Petri网的自动装弹机故障分析方法
2017-09-29王国辉范鹏飞李向荣白向华
王国辉,范鹏飞,李向荣,白向华
(装甲兵工程学院 兵器工程系,北京 100072)
基于云模型和故障Petri网的自动装弹机故障分析方法
王国辉,范鹏飞,李向荣,白向华
(装甲兵工程学院 兵器工程系,北京100072)
针对装甲装备自动装弹机故障率高、原因复杂的情况,结合Petri网理论提出一种基于云模型和故障Petri网的旋转输弹机故障分析方法。改变以往通过专家评价和人工经验来设置参数的传统做法,提出基于云模型的模糊token值初始化方法;基于相关文献对正反推理算法进行研究,实现对自动装弹机的状态评价和故障原因诊断;以旋转输弹机为例,结合其具体构造建立对应IFFPN故障模型,通过部分故障数据和相关模型的推理,验证故障分析方法的有效性。
改进模糊故障Petri网;自动装弹机;故障分析
武器装备可靠性的高低严重制约和影响着部队的日常训练和作战使用。某型履带步兵战车集机、电、液、光、计于一体,故障模式新,故障查找难,维修难度大[1]。在工厂和部队的调研中,可以发现:与其他部件相比,旋转输弹机作为自动装弹机的重要组成部分,其发生故障的频率更高、影响更大、原因更复杂。对旋转输弹机的故障问题研究,目前仍然处于算法研究和少量应用阶段,因此有必要对其故障检测和故障诊断进行深入研究,以寻求更加有效、更加具有针对性的故障分析方法。
关于Petri网在故障检测和故障诊断方面的研究与应用,现已有不少成果:王国辉等[2]针对装甲车辆自动装弹机故障诊断算法领域空白的情况,提出了一种使用故障Petri网进行故障推理的算法;张振山等[3]针对坦克自动装弹机故障检测因果关系的复杂性和模糊性,提出了一种基于模糊Petri网的故障推理算法并应用于故障检测模型;程学珍等[4]针对三相异步电动机故障问题建立了模糊故障Petri网模型,提出变迁使能点火判别矩阵,结合MYCIN置信度矩阵法的正向推理算法,实现电动机运行状态的准确评价,提出了一种更为简洁的全矩阵推理算法,使诊断速度极大提高。
针对以上情况,结合Petri网理论提出一种基于改进模糊故障Petri网的旋转输弹机故障分析方法。改变以往通过专家评价和人工经验来设置参数的传统做法,提出基于云模型的模糊token值初始化方法;对正反推理算法进行研究,实现对自动装弹机的状态评价和故障问题的原因诊断;以旋转输弹机为例,建立旋转输弹机的改进模糊故障Petri网模型,结合部分故障数据,通过其中的部分模型推理,从而验证故障分析方法的有效性。
1 IFFPN描述
1.1IFFPN定义
定义1在经典Petri网[5]和模糊故障Petri网[6]理论的基础上,对token值和权值的确定方法进行改进,并提出改进模糊故障Petri网(ImprovedFuzzyFaultPetriNet,IFFPN)。它可定义为一个10元组:
IFFPN= (P,T,I,O,M,Ω,α,f,λ,U)
1)P表示非空有限库所的集合,反映故障事件或者故障设备的状态,P={p1,p2,…,pn}(n>0)。
2)T表示非空有限变迁集合,表示事件的状态变化或行为动作,反映故障流转的传播过程,T={t1,t2,…,tn}(n>0)。
3)I为Petri网的输入矩阵,用从库所到变迁的有向弧来表示,即I:P*T。
4)O为Petri网的输出矩阵,用从变迁到库所的有向弧来表示,即O:T*P。
5)M表示库所标志分布矢量,不同的token数目和颜色反映了不同的故障路径数目和故障严重程度,M={m1,m2,…,mn}(n>0)。
6)Ω表示库所故障事件的权值,反映库所对变迁的影响程度,Ω={ω1,ω2,…,ωn}(n>0)。
7)α表示库所的置信度,反映故障事件真实性的可信程度,提出基于云模型的初始值确定方法,即α值由前件云发生器生成,α={α1,α2,…,αn}(n>0)。
8)f表示库所事件模糊故障率的集合,f={f1,f2,…,fn}(n>0),其中f代表故障发生的概率大小。
9)λ表示变迁规则阈值的集合,λ={λ1,λ2,…,λn}(n>0)。
10)U=diag(u1,u2,…,un)为变迁规则的可信度矩阵,反映不同变迁规则的可信度。
当库所置信度与对应权值乘积的和大于变迁阈值,那么称该变迁为预使能,若库所中包含了不少于一个token值,那么后继库所也会产生新的置信度。
1.2基于云模型的模糊token值
云模型是近年兴起的一种不确定性语言描述工具[7-8],它适合于对类似模糊值等不确定性概念的描述,而IFFPN中的模糊token值恰恰适用这一概念。云概念虽为定性概念,但它的数字特征可由3个变量来概括:云滴点的位置期望Ex、反映云概念不确定度的熵En、反映离散程度与厚度的超熵He。
在确定模糊token值的过程中,利用云模型方法来代替传统方法,更能够体现库所初始状态信息的不确定性[9]。基于云模型的模糊token值确定步骤如下:
1)基于专家评价和人工经验给出定性描述。
2)运用逆向云发生器转换为不确定性概念。
3)把被考察对象指标物理量代入前件云发生器中,得到正态云确定度。
2 推理算法分析
IFFPN基于Petri网改进得来,它同样具有Petri网的可达性,结合矩阵计算方法,可以进行故障模型的正向与反向故障推理。在文献[10]的基础上,定义如下算子:
取大算子∧C=A∧B,其中A、B、C均为m×n的矩阵,令cij=max(aij,bij),i=1,2,…,m;j=1,2,…,n。
取小算子∨C=A∨B,其中A、B、C均为m×n的矩阵,令cij=min(aij,bij),i=1,2,…,m;j=1,2,…,n。
比较算子⊙C=A⊙B,其中A、B、C均为m×n的矩阵,若aij>bij则令cij=1,否则令cij=0,i=1,2,…,m;j=1,2,…,n。

2.1正向推理
IFFPN的正向推理过程主要通过对设备故障状况的实时检测,从而预测设备将要发生的故障种类和故障形式。而对变迁点火的判断和故障状态token值的流动,是推理过程中需要完成的主要任务。引用文献[4]中变迁点火的判别矢量,并进行简化修正,最终得到:
L=α⊙λ
(1)
式中:α为库所置信度矢量;λ为变迁阈值矢量。
两者进行比较后,得出变迁预使能点火矢量为L=[l1,l2,…,ln]T,n>0,当ln=1时,表示发生变迁点火,反之若ln=0则表示未点火。
利用IFFPN模型的关联矩阵,可得到标识分布矢量为:
Mk=Mk-1∧(A⊗Vk)
(2)
基于点火规则可以得到使能点火矢量为
(3)
2.2逆向推理
当设备发生故障并进行维修保养时,需要对其进行故障诊断,判断故障发生的位置和具体原因。根据IFFPN进行逆向推理,能够辅助进行判断,迅速地查找可能的故障源。
在逆向推理中,IFFPN模型里的输入库所和输出库所分别为其逆向模型中的输出库所和输入库所,即:
I-=0,0-=I
在现有文献[11]逆向推理矩阵的基础上,进行改进调整后得到:
(4)

3 建立输弹机IFFPN模型
输弹机作为自动装弹机子系统的重要组成部分,是决定火炮武器系统工作是否正常的关键因素之一。而作为结构机电一体化和动作流水化作业的输弹机,却一直面临着多种多样的故障问题,同时,其故障机理复杂,往往一种现象与多种原因对应,或者多种现象与一种原因对应。某型履带步兵战车的100mm火炮输弹机简化结构示意如图1所示。

结合IFFPN知识可以建立输弹机的IFFPN模型,库所对应的故障事件和设备如表1中所示,输弹机的IFFPN模型如图2所示。

表1 库所对应故障事件

4 输弹机故障分析与验证
为了能够更加清晰地表现故障分析过程,下面将以“输弹机不转动”故障为例,结合IFFPN模型进行说明。输弹机不转动的IFFPN模型如图3所示。

4.1初始化
4.1.1置信度的确定
基于云模型确定库所事件为真的可信度,可以利用前件云发生器来计算,单因素(多因素)模糊token值的确定方法具体如下:
1)生成一组随机数,使其满足期望为Eni=(En1,En2,…,Enn),方差为He2=(He12,Ee22),即超熵的平方,Enni=Norm(En,He2);

以库所事件p29为例进行分析,容弹装置发生故障时的设备运转时间通常为700~1000h,通过相关数据统计和整理,选定8位专家评定故障发生时运转时间的阈值为(752,900,960,683,1022,843,954,887)。对于部分库所初始模糊token值,通过相关数据计算可以模拟形成其故障标识token的云模型,即:


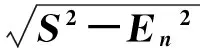
根据数字特征,利用Labview编程对其进行可视化显示,最终随机模拟得到的云模型如图4所示。

利用前件云发生器可以计算不同情况下的模糊token值,即为库所事件的模糊置信度,若x=875,则μ=0.836。以此类推,可以通过计算得到全部置信度,将初始置信度设置为
α0=[0.62,0.835,0.728,0.58,0.918,0.753,0.897,0.92,0.755,0.953]
4.1.2其他值的确定
基于文献[12]中的设置方法,结合专家评价与人工经验,可将初始权值设置为
ω=[0.8,1.0,0.9,0.85,0.8,1.0,1.0,1.0,1.0,1.0]
阈值均设为0.5,变迁规则可信度设为
U=diag[0.7,0.8,0.8,0.95,0.8,0.7,0.9,0.95,0.8,0.7]
4.2正向推理与验证
4.2.1推理计算
当输弹机进行输弹动作,假设完成第1次输弹后并未发生故障,但监测设备或人员发现有以下两个现象:“按钮失灵”和“电机异常振动”,即初始库所标志分布矢量为
M0=[0,0,1,0,1,0,0,0,0,0]T
将置信度α0代入公式(1)中,即可得到
L=[1,1,1,1,1,1,1,1,1,1]T
将变迁预使能点火矢量代入公式(2)中,其中,输入矩阵为

借助MATLAB编程计算,可得
V1=[1,0,1,1,1,0,0,1,0,1]T
M1=[1,1,1,0,0,0,0,1,0,0]T
V2=[1,0,0,0,1,0,0,0,0,0]T
M2=[0,1,1,0,1,1,0,0,1,0]T
V3=[1,0,1,0,1,0,1,0,0,1]T
M3=[1,0,1,0,1,0,1,0,1,1]T
V4=[0,0,0,0,0,0,0,0,0,1]T
M4=[1,0,1,0,0,0,1,1,0,1]T
V5=[0,0,0,0,0,0,0,0,0,1]T=V4
此时,M5=[1,0,1,1,0,1,1,1,0,1]T,推理结束,将相关信息转入IFFPN模型中显示,可以更加直观、清晰地观察故障在传播过程中的可能路径,如p3、p4→p7→p10,p1→p7→p10等;以及需要重点检测的部位,如p3、p4等。正向推理结束后,token分布示意如图5所示。

4.2.2计算验证
在实际工作中,往往要归纳总结自动装弹机的常见故障模式,并对故障机理进行分析,从而进一步寻找故障发生的位置。传统方法中,利用故障树进行分析能够有效改进并监测故障,如图6所示为输弹机不转动的故障树。

故障树并不能够体现IFFPN中的模糊信息,因而可引入规则置信度等到故障树中。假设发生事件A2和A3,与其相关联的事件有A4、B7和C10,可设ω43=0.55,ω44=0.45,ω5=0.8。当置信度与权值之积大于对应阈值时,则认为该事件发生,同时由析取式原则可得:
X1=A3×ω43=0.401
X2=A4×ω44=0.261
X=X1+X2=0.662>ω
B7=X×u4=0.629
B8=X3×u5=0.576
C10=B7×u8=0.705
通过折线对比图7可以看到,通过引入模糊概念后传统故障树方法的计算,其结果与之前推理结果是可以相互映证的,且误差较小,能够满足故障推理检测的需求。

4.3逆向推理与验证
4.3.1推理计算
当输弹机进行输弹动作并检测到“控制台故障”时,逆向初始标志矢量为

代入置信度到公式(1)中,可得逆向变迁预使能点火矢量为
L-=[1,1,1,1,1,1,1,1,1,1]T








4.3.2数据验证
由于输弹机工作环境的恶劣性和特殊性,操作人员和维修人员都往往无法获得十分具体、准确、详细的故障信息,这为数据验证模型推理增加了难度。在保留部分不明原因故障的前提下,挑选出具有代表性的故障记录,经整合、完善后得到表2。

表2 故障信息表
采用计算相关性的方法,判断故障数据与基于云模型确定的模糊token值之间是否存在一致性,过程如下:
1)平均值Y1=10,Y2=0.673 5。
2)标准差S1=25.649,S2=0.327 8。
3)相关系数ρY1Y2=0.798 2。
由相关系数可知,真实故障记录次数与基于云模型推理的token值具有较强的相关性,说明推理结果是较有说服力的。
5 结束语
通过改变以往专家评价和人工经验来设置参数的传统做法,提出基于云模型的模糊token值初始化方法,并利用故障数据进行验证;对正反推理算法进行探讨,实现对旋转输弹机的状态评价和故障问题的原因诊断;将IFFPN模型运用于输弹机的故障分析,建立旋转输弹机IFFPN故障模型,通过正反推理验证了该故障分析方法的有效性。
受到相关故障数据准确性和具体性的限制,该方法在验证某些故障时仍然不够准确,下一步应当在扩大故障信息来源、对模型和算法加以完善的同时,将其应用于故障检测和诊断的软件开发。
References)
[1] 张仕新,张耀辉,吕会强.某型步兵战车故障规律及维修保障方案优化研究[R].北京:装甲兵工程学院,2011. ZHANG Shixin, ZHANG Yaohui, LYU Huiqiang. Research on the failure rules and maintenance support conception for one type infantry fight vehicle[R]. Beijing: Academy of Armored Forces Engineering,2011.(in Chinese)
[2] 王国辉,王威.基于故障Petri网的自动装弹机故障诊断研究[J].火炮发射与控制学报,2004(4):55-58. WANG Guohui, WANG Wei. Study on diagnosis of autoloader based on Petri net[J]. Journal of Gun Launch & Control,2004(4):55-58.(in Chinese)
[3] 张振山,李培富,黄晶晶,等.模糊Petri网在坦克自动装弹机故障检测中的应用[J].四川兵工学报,2011,32(9):7-9. ZHANG Zhenshan, LI Peifu, HUANG Jingjing,et al. Application of fuzzy Petri-net to fault detection in tank autoloader[J]. Journal of Sichuan Ordnance,2011,32(9):7-9.(in Chinese)
[4] 程学珍,王程,于永进,等.一种基于模糊故障Petri网的三相异步电动机故障分析方法[J].电工技术学报,2015,30(17):132-138. CHENG Xuezhen, WANG Cheng, YU Yongjin,et al. An approach for three-phase asynchronous motor failure analysis based on fuzzy fault Petri net[J]. Transactions of China Electrotechnical Society,2015,30(17):132-138.(in Chinese)
[5] 罗雪山,罗爱民,张耀鸿,等. Petri网在C4ISR系统建模、仿真与分析中的应用[M].长沙: 国防科技大学出版社,2007. LUO Xueshan,LUO Aimin,ZHANG Yaohong,et al.Application of Petri nets in modeling,simulation and ana-lysis of C4ISR system[M]. Changsha: National University of Defense Technology Press,2007.(in Chinese)
[6] 黄敏,林啸,侯志文.模糊故障 Petri 网建模方法及其应用[J]. 中南大学学报:自然科学版,2013,44(1):208-215. HUANG Min, LIN Xiao, HOU Zhiwen. Modeling method of fuzzy fault Petri nets and its application[J]. Journal of Central South University: Science and Technology,2013,44(1):208-215.(in Chinese)
[7] 董磊,阎芳,王鹏.基于修正高维云的故障映射模型[J].系统工程与电子技术,2015,37(2):354-359. DONG Lei, YAN Fang, WANG Peng. Fault mapping model based on correction high dimensional cloud[J]. Systems Engineering and Electronics,2015,37(2):354-359.(in Chinese)
[8] 王兵,李盼池,杨冬黎,等.云过程神经网络模型及算法研究[J]. 电子与信息学报,2015,37(1):110-115. WANG Bing, LI Panchi, YANG Dongli,et al. Research on cloud process neural network model and algorithm[J]. Journal of Electronics & Information Technology,2015,37(1):110-115.(in Chinese)
[9] 党小超,樊婷,郝占军.基于云模型的模糊Petri网token确定方法研究[J].小型微型计算机系统,2014,35(4):827-830. DANG Xiaochao, FAN Ting, HAO Zhanjun. Study on method of determining fuzzy tokens in fuzzy Petri nets based on cloud model[J]. Journal of Chinese Computer Systems,2014,35(4):827-830.(in Chinese)
[10] 汪惠芬,梁光夏,刘庭煜,等.基于改进模糊故障Petri网的复杂系统故障诊断与状态评价[J].计算机集成制造系统,2013,19(12):3049-3060. WANG Huifen, LIANG Guangxia, LIU Tingyu,et al. Machinery failure diagnosis and condition evaluation for complex system based on improved fuzzy fault Petri net[J]. Computer Integrated Manufacturing Systems,2013,19(12):3049-3060.(in Chinese)
[11] MOTAMENI H,GHASSEMPOURI T.Transforming fuzzy communication diagram to fuzzy Petri net[J].American Journal of Scientific Research,2011,16:63-74.
[12] 谢倩,乐晓波,周恺卿,等.模糊 Petri 网库所集中token 初始值的确定方法[J].计算机工程与应用,2012,48(12):49-52. XIE Qian, YUE Xiaobo, ZHOU Kaiqing,et al. Determination of token in initial place of fuzzy Petri nets[J]. Computer Engineering and Applications,2012,48(12):49-52.(in Chinese)
[13] 原菊梅.复杂系统可靠性 Petri 网建模及其智能分析方法[M].北京: 国防工业出版社,2011. YUAN Jumei. Petri net modeling and intelligent analysis method for complex system reliability[M]. Beijing: National Defense Industry Press,2011.(in Chinese)
OneApproachforFailureAnalysisofAuto-loaderBasedonCloudModelandImprovedFuzzyFaultPetriNet
WANG Guohui, FAN Pengfei, LI Xiangrong, BAI Xianghua
(Department of Arms Engineering, Academy of Armored Force Engineering, Beijing100072, China)
Aiming at the circumstances of the high rate of failure and complexity of reasons in the auto-loader of armoured armament, in combination with the Petri net theory, one approach for failure analysis of rotatory feed mechanism was proposed based on improved fuzzy fault petri net and cloud model. This approach changes the traditional parameter settings method which relies on expert evaluation and manual experience to the new initializing method of fuzzy token value based on cloud model. Based on relevant literature, the positive and negative reasoning algorithms were sudied, enabling the status evaluation and failure judgment. Then the rotary ramming mechanism was taken for an instance, with the improved fuzzy fault petri net model establihed according to concrete structure, and with its effectiveness verified via part of failure data and relevant model reasoning.
improved fuzzy fault Petri net; auto-loader; failure analysis
TJ303.3
: A
:1673-6524(2017)03-0085-07
10.19323/j.issn.1673-6524.2017.03.017
2017-02-20
王国辉(1966—),男,教授,主要从事武器系统与保障工程技术研究。E-mail:474691046@qq.com
