基于自适应遗传算法的粒子滤波器

杜正聪, 邓 寻

(攀枝花学院，四川 攀枝花 617000)

基于自适应遗传算法的粒子滤波器

杜正聪, 邓 寻

(攀枝花学院，四川 攀枝花 617000)

针对重采样导致的权值退化问题，应用遗传算法的进化思想来优化重采样算法，将粒子权值作为适应度值，合理设定阈值，利用最佳个体保存法保存高适应度粒子，利用自适应交叉、变异操作对低适应度粒子进行进化，将高适应度粒子与进化粒子组合成新的粒子集进行状态估计。仿真实验表明，该算法具有良好的实时性和估计精度，其状态估计精度比标准粒子滤波提高近24倍，比无迹卡尔曼粒子滤波提高近4倍，耗时约为无迹卡尔曼粒子滤波的1/10。

粒子滤波；选择；交叉；自适应遗传算法

非线性、非高斯系统的状态估计问题已经成为现代信号处理的主要任务之一，扩展卡尔曼滤波(EKF)是处理该问题的常用手段。对于强非线性系统，EKF的滤波精度较低，寻找精度更高的非线性滤波器至关重要。粒子滤波[1](PF)是基于Monte Carlo思想的Bayes估计算法，已在信号处理[2]、目标跟踪[3]、模式识别以及无线通信等领域得到普遍应用；但粒子滤波仍有许多问题亟待解决。粒子滤波通过数次迭代后，会出现权值退化现象，即仅有少量大权值粒子，大多数粒子的权值几乎为零，导致算法的有效性和实时性降低。为了解决这些问题，邹国辉等[4]改进了粒子滤波重采样算法，通过线性组合大权值粒子与被丢弃的粒子来获取新的粒子，降低了粒子样本匮乏；但步长系数值的选取是一个难点。张琪等[5]通过引入克隆操作和变异操作来缓解粒子滤波的权值退化问题；但算法的计算复杂度较高。方正等[6]利用粒子群来优化重采样操作，可有效提升算法的全局搜索能力，增加算法的状态估计精度；但算法易产生局部最优。王龙生等[7]采用基于微分进化思想的组合重采样技术来缓解粒子滤波的权值退化；但比例因子F和交叉概率Cr的选取是一个难点。朱志宇[8]利用遗传算子来维持粒子的多样性，规避了重采样；但赌盘法的随机性选择将丢失粒子群中的优秀粒子，恒定的交叉概率以及变异概率会降低粒子滤波算法的有效性。于金霞等[9]利用自适应优化算法改进了粒子滤波算法的建议分布及重采样，能适当增加样本的多样性；但计算过程比较复杂。

针对粒子滤波的权值退化问题，本文在汪荣贵等[10]研究的基础上，应用遗传算法的进化思想，采用选择、交叉、变异操作来改进传统的重采样技术，提出了一种优化的自适应遗传粒子滤波算法(IAG-PF)。将粒子权值作为适应度值，合理设定阈值，通过最佳个体保存法取得若干数量的大权值粒子进入下一次循环，利用自适应交叉、变异操作对低适应度粒子进行进化，高适应度粒子与进化粒子组合成的新粒子集较之于未做进化处理的粒子集会更加接近于从真实后验概率分布取样得到的粒子集。IAG-PF算法能在基本不增加运算复杂度的前提下有效维持粒子多样性、缓解权值退化、提高状态估计精度。

1 粒子滤波

粒子滤波的实质是Bayes估计理论在非线性、非高斯系统中的一种Monte Carlo实现，其核心思想是用独立抽取至状态空间的样本序列的均值来近似后验概率分布[11]。即

(1)

(2)

(3)

利用Bayes准则，得到重要性权值的计算公式如(4)式

(4)

式(3)和(4)即为基本粒子滤波算法的关键操作。

2 遗传粒子滤波算法

Holland教授于1975年提出的遗传算法(GA)是一种通过模拟自然进化过程搜索最优解的方法，将待求解问题模拟成一个生物进化的过程，通过复制、交叉、突变等操作来迭代更新，逐步淘汰适应度函数值低的解，增加适应度函数值高的解，经过N代进化后就很有可能会进化出高适应度函数值的个体。朱志宇[8]将遗传变异思想引入基本粒子滤波器,提出了遗传粒子滤波算法(GPF)。其基本运算如下。

a.选择运算：将选择算子作用于粒子集，获取若干数量的粒子样本并组合成新的样本集。

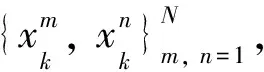
(5)

(6)

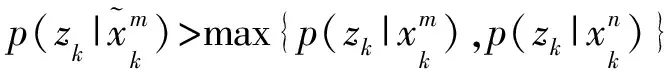
c.变异运算：任意选取一个粒子，根据(7)式作变异操作

(7)

3 自适应遗传算法

交叉算子与遗传算子的选择对遗传算法性能有很大影响。基本遗传算法中pc与pm一般取定值，对复杂系统的状态估计会出现精度低、性能差，甚至算法发散等问题。为此，Srinivas等[12]提出自适应遗传算法(AGA)，通过个体适应度值来调节交叉概率pc和变异概率pm，可增强算法的收敛速度及全局搜索能力。其实现方式为

(8)

(9)

其中:fmax表示最大适应度值；favg表示平均适应度值；f′表示2个做交叉操作的个体较大的适应度值；f表示变异个体的适应度值。通过设定k1、k2、k3、k4，就可以实现pc和pm的自适应调整。

经公式(8)和(9)的处理后，算法对适应度较低的粒子采用适当高的概率进行交叉、变异，对适应度较高的粒子运用相反的概率进行交叉、变异，一定程度上实现了算法的自适应，尤其是在进化的后期有利于保持粒子的适应度值。但对于进化的初期，特别是在高适应度值粒子数量较多的情况下，算法容易陷入局部最优[10]。

为克服上述不足，对公式(8)和(9)做如下改进

(10)

(11)

其中pc1和pm1为[0,1]内的数。对比式(10)、(11)和式(8)、(9)得知，改进算法在保存高适应度值粒子的同时可有效维持全体粒子的进化，增强算法的全局搜索能力。

4 自适应遗传粒子滤波器

综上所述，通过引入自适应遗传算法的选择、交叉和变异操作可有效缓解传统粒子滤波重采样导致的权值退化问题，提高算法效率和估计精度。为克服遗传算法中赌盘式选择操作的随机性选择可能导致的大适应度值粒子丢失，本文引入文献[13, 14]的最优保存方案来进行选择操作。将粒子按适应度值从大到小排列，保存一定比例大权值粒子，不进行交叉、变异运算直接参与下一步迭代。低适应度值粒子经交叉、变异运算后再进入迭代环节，可在保证算法收敛性的同时提高全局最优概率。

IAG-PF算法运算

步骤2：计算重要性权值，并归一化。

(12)

(13)

步骤3：遗传运算。

a.选择：选取高适应度值粒子按最佳个体保存方案进行运算。

c.变异：按公式(11)计算变异概率pm。为避免IAG-PF算法产生非目标性收敛，本文采用以下公式来进行变异操作[15]。

(14)

其中β可视情况确定，一般选择为随机正实数。

d.对按上述a-c步操作形成的粒子集计算权值并做归一化处理。

步骤4：按式(15)运算并令k=k+1，直至运算结束。

(15)

5 算法性能验证与分析

下面，采用式(16)和(17)所示动态状态空间模型对上述算法性能进行验证。

xt=1+sin(0.4π(t-1))+0.5xt-1+wt-1

(16)

(17)

其中观测噪声vt～N(0,10-5)，过程噪声wt-1～N(3/2, 3/4)，设初始状态x0=1，时间T=50，仿真软件为Matlab7.0。为验证本文所述算法的性能，分别采用PF算法、GPF算法、UPF算法和IAG-PF算法对式(16)和(17)所示状态空间模型进行状态估计。图1为4种算法某次独立仿真实验的状态估计结果。

图1 PF、GPF、UPF和IAG-PF的状态估计Fig.1 The state estimation results of PF, GPF, UPF and IAG-PF

仿真结果表明，因粒子权值退化问题未得到有效处理，PF算法的状态估计精度无法得到保证，时有估计结果偏离真实状态的情况；GPF算法因引入遗传算法来进化粒子，估计精度高于PF算法；UPF算法因引入最新观察函数值来优化抽样函数，能有效缓解粒子权值退化现象，状态估计精度好于GPF算法；IAG-PF算法因最佳保存策略和自适应操作的引入，在高效利用高适应度值粒子的同时合理进化低适应度值粒子，可有效抑制权值退化与样本衰竭，增强算法的全局搜索能力，较之于前述3种算法有着更好的滤波性能。

为了更好地验证PF算法、GPF算法、UPF算法及IAG-PF算法的状态估计性能，定义均方根误差公式如式(18)，采用多次Monte Carlo仿真实验估计值与真实值之间的均方根误差的均值与方差来评价算法性能。

(18)

图2 PF、GPF、UPF和IAG-PF的均方根误差曲线Fig.2 The RMSE curves of PF, GPF, UPF and IAG-PF

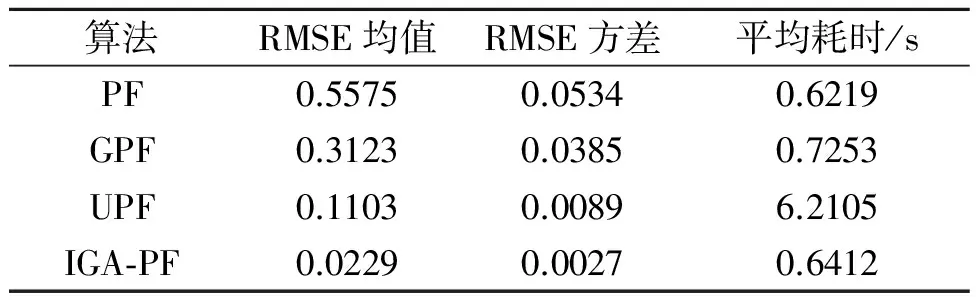
表1 50次Monte Carlo实验的RMSE均值、方差和平均耗时Table 1 The mean value, variance of RMSE and average time from 50 Monte Carlo experiments

分析仿真结果可看出，较之于其他3种算法，IAG-PF算法的RMSE均值与方差皆为最小，其状态估计值最逼近真实值，算法性能最好。在相同仿真实验条件下，IAG-PF算法的运算时间与PF大体相当，但前者的RMSE均值与方差均远小于后者；UPF算法在耗时远大于IAG-PF算法的情况下，前者的RMSE均值与方差仍远大于后者；将IAG-PF算法与GPF算法比较也能得到类似的结果。

6 结 论

本文在前人研究[9-10,14-15]的基础上，针对粒子滤波重采样导致的粒子权值退化问题，采用遗传算法的进化思想来优化重采样算法，将粒子权值作为适应度值，合理设定阈值，利用最佳个体保存法来保存高适应度值粒子，通过自适应交叉、变异操作对低适应度粒子进行进化，将高适应度粒子与进化粒子组合成新的粒子集进行状态估计。仿真实验表明，IAG-PF算法有较快的收敛速度及良好的全局搜索性能，相较于PF算法、UPF算法和GPF算法，IAG-PF算法在处理非线性、非高斯系统的状态估计问题具有优良的实时性和滤波精度。

[1] Gordon N J, Salmond D J, Smith A F M. Novel approach to nonlinear non-Gaussian Bayesian state estimation [J]. IEEE-Proceedings-Radar, Sonar and Navigation, 1993, 140(2): 107-113.

[2] Laska B N M, Bolic M, Goubran R A. Particle filter enhancement of speech spectral amplitudes[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2010, 18(8): 2155-2167.

[3] 陈志敏,薄煜明,吴盘龙,等.基于自适应粒子群优化的新型粒子滤波在目标跟踪中的应用[J].控制与决策,2013,28(2):193-201. Chen Z M, Bo Y M, Wu P L,etal. Novel particle filter algorithm based on adaptive particle swarm optimization and its application to radar target tracking[J]. Control and Decision, 2013, 28(2): 193-201. (in Chinese)

[4] 邹国辉,敬忠良,胡洪涛.基于优化组合重采样的粒子滤波算法[J].上海交通大学学报,2006,40(7):1135-1139. Zou G H, Jing Z L, Hu H T. A particle filter algorithm based on optimizing combination resampling[J]. Journal of Shanghai Jiaotong University, 2006, 40(7): 1135-1139. (in Chinese)

[5] 张琪,胡昌华,乔玉坤.基于权值选择的粒子滤波算法研究[J].控制与决策,2008,23(1):117-120. Zhang Q, Hu C H, Qiao Y K. Particle filter algorithm based on weight selected[J]. Control and Decision, 2008, 23(1): 117-120. (in Chinese)

[6] 方正,佟国峰,徐心和.粒子群优化粒子滤波方法[J].控制与决策,2007,22(3):273-278. Fang Z, Tong G F, Xu X H. Particle swarm optimized particle filter[J]. Control and Decision, 2007, 22(3): 273-278. (in Chinese)

[7] 王龙生,顾浩,余云智.基于微分进化的组合重采样粒子滤波算法[J].光电与控制,2012,19(11):43-47. Wang L S, Gu H, Yu Y Z. A new combined particle filter based on differential evolutionary algorithm resample and residual resample[J]. Electronics Optics & Control, 2012, 19(11): 43-47. (in Chinese)

[8] 朱志宇.粒子滤波算法及其应用[M].北京:科学出版社,2010:74-77. Zhu Z Y. Particle Filter Algorithm and Its Application[M]. Beijing: Science Press, 2010: 74-77. (in Chinese)

[9] 于金霞,汤永利,许景民.一种改进的自适应优化粒子滤波算法研究[J].小型微型计算机系统,2013,34(6):1446-1450. Yu J X, Tang Y L, Xu J M. Research on an improved particle filter algorithm based on adaptive optimization mechanism[J]. Journal of Chinese Computer Systems, 2013, 34(6): 1446-1450. (in Chinese)

[10] 汪荣贵,李孟敏,吴昊,等.一种新型的基于自适应遗传算法的粒子滤波算法[J].中国科技大学学报,2011,41(2):134-141. Wang R G, Li M M, Wu H,etal. A new particle filter algorithm based on the adaptive genetic algorithm[J]. Journal of University of Science and Technology of China, 2011, 41(2): 134-141. (in Chinese)

[11] 杜正聪,唐斌,李可.混合退火粒子滤波器[J].物理学报,2006,55(3):999-1003. Du Z C, Tang B, Li K. The hybrid annealed particle filter[J]. Acta Physica Sinica, 2006, 55(3): 999-1003. (in Chinese)

[12] Srinivas M, Patnaik L M. Adaptive probabilities of crossover and mutation in genetic algorithms[J]. IEEE Transactions on Systems, Man and Cybernetics, 1994, 24(4): 66-667.

[13] 孟庆春,纪洪波,董浩.带有对称编码的基因算法中的优良个体成员选取和保存技术[J].计算机研究与发展,1997,34(增刊):28-31. Meng Q C, Ji H B, Dong H. Techniques of selecting and safeguarding the good members in genetic algorithm with symmetric code[J]. Computer Research & Development, 1997, 34(Suppl.): 28-31. (in Chinese)

[14] 王蕾,沈庭芝,招杨.一种改进的自适应遗传算法[J].系统工程与电子技术,2002, 24(5):75-78. Wang L, Shen T Z, Zhao Y. An improved adaptive genetic algorithm[J]. Systems Engineering and Electronics, 2002, 24(5): 75-78. (in Chinese)

[15] 张敬海.基于遗传算法的粒子滤波算法研究[D].天津:天津大学档案馆,2009. Zhang J H. Research on Particle Filtering Based on Genetic Algorithm[D]. Tianjin: The Archive of Tianjin University, 2009. (in Chinese)

Particlefilterbasedonadaptivegeneticalgorithm

DU Zhengcong, DENG Xun

PanzhihuaUniversity,Panzhihua617000,China

An improved adaptive genetic particle filter algorithm is proposed in order to alleviate weights degradation of particle filtering algorithm. Particle weight is regarded as fitness values, and a percentage of big weight particles are obtained with the best individual preservation method. Crossover and mutation operations are adopted for the remaining particles. Then formed a new set of particles with saved particles, crossover and mutation particles, and state estimation calculations is done. Maintaining the diversity of the particles at the same time, it avoids algorithm falling into local optimum and improves the global search ability of the algorithm. The simulation results show that, compared with the standard particle filter, the proposed algorithm can improve the accuracy of state estimation by nearly 24 times, 4 times higher than that of the Kalman particle filter, and it has high real-time performance and good estimation accuracy.

particle filtering; choice; cross; adaptive genetic algorithm

TN957.51 [

] A

10.3969/j.issn.1671-9727.2017.05.14

1671-9727(2017)05-0636-05

2015-10-14。

四川省应用基础研究项目(2011JY0115)。

杜正聪(1975-),男,博士,教授，研究方向：非线性、非高斯信号处理, E-mail:duzc@163.com。