基于ECC存在特权集的(t,n)门限群代理多重签名方案

曹 阳

(陕西理工大学 数学与计算机科学学院, 陕西 汉中 723000)

基于ECC存在特权集的(t,n)门限群代理多重签名方案

曹 阳

(陕西理工大学 数学与计算机科学学院, 陕西 汉中 723000)

为了解决门限群签名方案中联合攻击、伪造攻击、权限、抵赖等问题，本文基于hash函数的单向性、椭圆曲线离散对数问题的难解性，结合Shamir(t,n)门限方案，提出了一种基于ECC存在特权集的(t,n)门限群代理多重签名方案，满足((t1′,n1′;t1,n1)(t2′,n2′;t2,n2))门限特性。该方案利用公钥环境下交互式身份验证的方法，增加成员认证密钥，有效防止密钥管理中心和签名服务者的串通陷害；签名者通过等式验证密钥管理中心分配的秘密份额是否有效；代理授权份额的生成由原始签名者和代理签名者共同完成，单个签名的生成使用了签名者的私钥和随机数，有效防范抵赖。安全性分析表明，该方案具有抗联合攻击、强不可伪造性、门限特性和匿名性等特点，满足门限群代理签名应有的性质。

特权集; (t,n)门限群代理;多重签名; ECC

门限群签名于1991年被Desmedt等[1]首次提出，随后许多学者针对群签名安全性、应用及其实现提出了不少签名方案[2-4]。实际应用中，为了解决将签名权利委托他人的问题，文献[5]提出了(k,m;t,n)门限群代理多重签名方案[5]。为了解决签名者权限不同的问题，2005年，Chen等[6]基于Shamir秘密共享，使用单签名构造群签名的思想，引入特权集，提出了基于离散对数问题的E.L.Gamal型存在特权集的门限群签名方案[6]。近年来，为了解决签名中的安全隐患。在文献[6]的基础上，将代理签名与存在特权集门限群签名思想相结合的方案[7-13]被不少学者提出，但仍然存在安全隐患。如文献[7]所提出的方案安全性需要可信中心的诚实性来维护；文献[8]所提出的方案存在密钥泄露问题；文献[9]所提出的方案不能抵抗合谋攻击；文献[12]所提出的方案每次参与代理签名的只有1个特权者，如果参与的特权者不止1个，方案不能实现。本文针对门限群代理多重签名中存在的联合攻击、伪造攻击、权限问题、匿名性等安全性问题，基于ECC提出了一种存在特权集的(t,n)门限群代理多重签名方案。

1 方案构成

本文提出的基于ECC存在特权集的(t,n)门限群代理多重签名方案要求满足((t1′，n1′;t1,n1)(t2′,n2′;t2,n2))，即原始签名群中n1个签名用户至少有t1个参与且特权集中n1′个特权用户至少有t1′个参与才能生成合法代理授权，代理签名群中n2个签名用户至少有t2个参与且特权集中n2′个特权用户至少有t2′个参与才能生成对消息M的合法群签名。KMC为可信任密钥管理中心，负责给成员分配密钥；SC为签名服务者，负责接收单个签名、生成群签名及追踪签名人的身份；SD为签名秘书；SV为签名验证者，负责验证签名是否有效。方案主要由 系统初始化、秘密份额分发、代理授权份额生成、代理签名的生成、代理签名验证等5个部分组成。

1.1 系统初始化

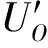
密钥管理中心(KMC)选取有限域上安全椭圆曲线E(Fp)(p为大素数)，且该曲线满足椭圆曲线离散对数问题[14]的难解性，G为E(Fp)的基点，其阶为q，H()为单向安全hash函数，Fx()为求取E(Fp)上点的坐标函数，公开E(Fp),G,q,H(),Fx()。

每个原始签名者Ui随机选取rUi作为自己的私钥，RUi=rUimodq作为自己的公钥，公布RUi；每个代理签名者随机选取rPi作为自己的私钥，RPi=rPimodq作为自己的公钥，公布RPi。

KMC分别为UO和UP构造次数为t1-1和t2-1的秘密多项式f(x)、次数为t1′-1和t2′-1的秘密多项式g(x)。

WM是原始签名群授予代理签名群的证书，WM中记载了原始签名者及代理签名者的身份、证书的有效期、代理权限、原始签名者及代理签名者的公钥等信息。

签名服务者SC随机选取c作为自己的私钥，将公钥C=cGmodq连同身份证明材料发送给KMC；KMC用群密钥为其产生证书WC(证书的生成与成员证书的生成类似)。

(1)原始签名者Ui随机选取aUi，生成AUi=aUiGmodq，并将AUi发送给SC；代理签名者Pi随机选取aPi，生成APi=aPimodq，并将APi发送给SC。

(2)SC收到签名者发送来的公钥后，首先根据用户的身份证明材料为用户生成一个身份IDUi和IDPi(IDUi为原始签名者的身份，IDPi为代理签名者的身份)，IDUi和IDPi中包含用户的身份标志信息；其次计算SU=WC(IDUi‖AUi),SP=WC(IDPi‖APi),WUi=(IDUi‖AUi‖Su),WPi=(IDPi‖APi‖SP),将WUi和WPi发送给相应的签名者。

(3)各签名者将收到的IDUi和IDPi发送给KMC，KMC确认其权限后为其分发密钥碎片。

1.2 秘密份额分发

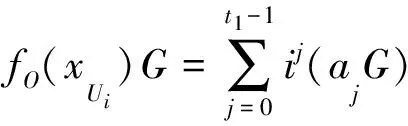
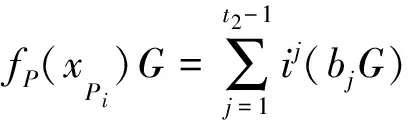
1.3 代理授权份额生成

现假设已成功选出实际参与授权的原始签名者为DO={U1,U2,…,Ut1}，DO⊆UO，其中恰有t1′个特权用户。假设实际参与对消息M签名的代理签名者为DP={P1,P2,…,Pt2}，DP⊆UP，其中恰有t2′个特权用户。

(1)Ui随机选取dUi，计算DUi=dUimodq，将DUi在原始签名DO和代理签名DP中广播；Pi随机选取dPi，计算DPi=dPiGmodq，将DPi在原始签名DO和代理签名DP中广播。

(3)原始签名者，若Ui是普通用户则计算ZUi=dUi+fO(xUi)λUi+(d⊕H(WM)rUimodq；若Ui是特权用户则计算ZUi=dUi+fO(xUi)λUi+gO(yUij)μUij+(d⊕H(WM)rUimodq，其中

YU*j表示第j个特权用户的特权身份，发送ZUi给SD。

代理签名者，若Pi是普通用户则计算ZPi=dPi+fP(xPi)λPi+(d⊕H(WM))rPimodq；若Ui是特权用户则计算ZPi=dPi+fP(xPi)λPi+gP(yPij)μPij+(d⊕H(WM))rPimodq，其中

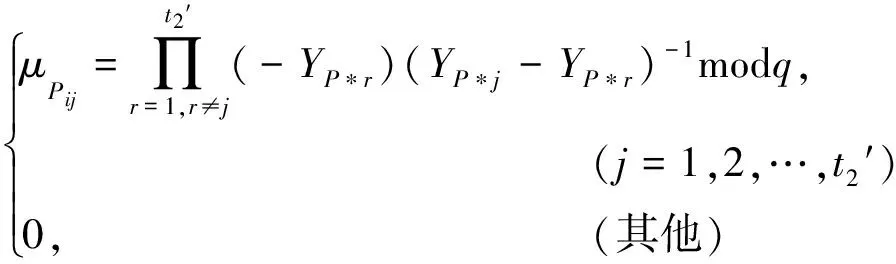
(4)SD收到后ZUi，通过等式DUi=ZUiG-(d⊕H(WM))RUi-(KUi1λUi+KUi2μUij)modq验证ZUi是否有效。若Ui是普通用户则μUij为0，只计算λUi；若Ui是特权用户，则计算λUi、μUij；若等式不成立则要求重新发送。收到ZPi后，通过等式DPi=ZPiG-(d⊕H(WM))RPi-(KPi1λPi+KPi2μPij)modq验证ZPi是否有效，若Pi是普通用户则μPij为0，只计算λPi；若Pi是特权用户，则计算λPi、μPi；若等式不成立则要求重新发送。

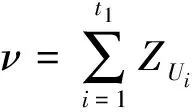
1.4 代理签名的生成

(1)Pi收到(d,ν)后，计算

d′=Fx(D′)modq。

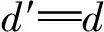
(2)SC和签名者Pi认证身份。

SC随机选取u1，将u1和Wc传送给Pi；Pi收到u1和Wc后，选取随机数u2，计算y1=aPi(IDc‖u1‖u2)，并将WPi、y1和u2传送给SC。

只有双方通过认证后，签名者才对消息M生成单签名，SC才会接受签名者对M生成的单签名。

(3)Pi随机选取li，计算Li=liGmodq(i=1,2,…,t2-1)，将Li发送给签名服务者SC。

(4)生成单个签名，若Pi是普通用户，则对消息M的单个签名为

Si=νli+fP(xPi)λPi+(d⊕H(M))rPimodq

若Pi是特权用户，则对消息M的单个签名为

Si=νli+fP(xPi)λPi+gP(yPij)μPij+ (d⊕H(M))rPimodq

代理签名为(Li,Si)，将Si通过安全信道发送给签名服务者SC。

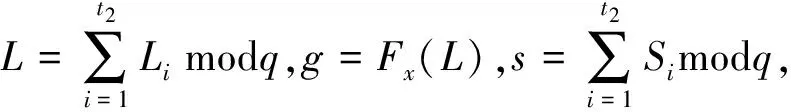
1.5 代理签名验证

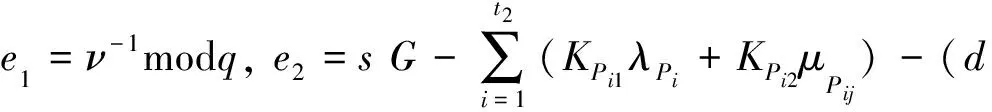
2 方案分析

2.1 正确性分析

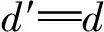
证明

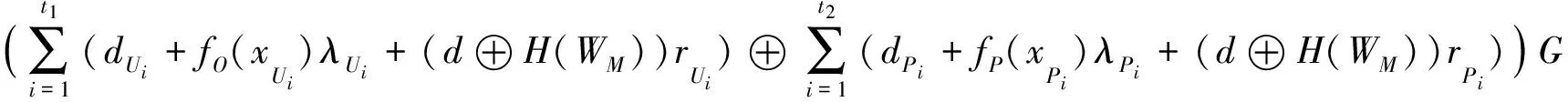
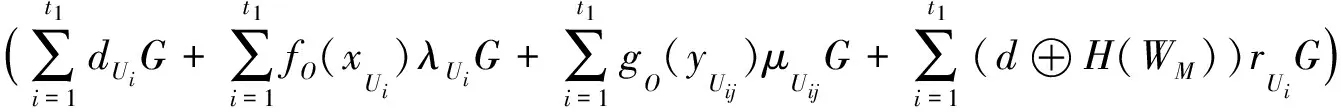
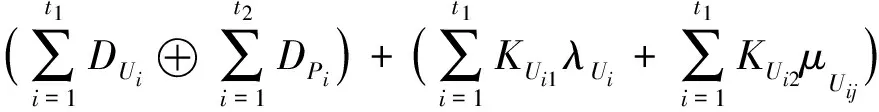
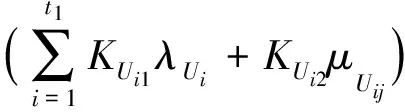
=D

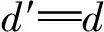
2.1.2 单个签名有效性验证

证明若是普通用户，

e2=SiG-(d⊕H(M))RPi-(KPi1λPi+KPi2μPij)modq

=(νli+fP(xPi)λPi+(d⊕H(M))rPi)G-(d⊕H(WM))RPi-KPi1λPimodq

=νliG+fP(xPi)λPiG+(d⊕H(M))rPiG-(d⊕H(WM))RPi-KPi1λPimodq

=νLi+KPi1λPi+(d⊕H(M))RPi-(d⊕H(WM))RPi-KPi1λPimodq

=νLimodq

若是特权用户，

e2=SiG-(d⊕H(M))RPi-(KPi1λPi+KPi2μPij)modq

=(νli+fP(xPi)λPi+gP(yPij)μPij+(d⊕H(M))rPi)G-(d⊕H(WM))RPi-(KPi1λPi+KPi2μPij)modq

=νliG+(fP(xPi)λPi+gP(yPij)μPij)G+(d⊕H(M))rPiG-(d⊕H(WM))RPi-(KPi1λPi+KPi2μPij)modq

=νLi+(KPi1λPi+KPi2μPij)+(d⊕H(M))RPi-(d⊕H(WM))RPi-(KPi1λPi+KPi2μPij)modq

=νLimodq

因为e1=ν-1modq,e1e2=Li，所以单个签名有效。

2.1.3 多重签名验证

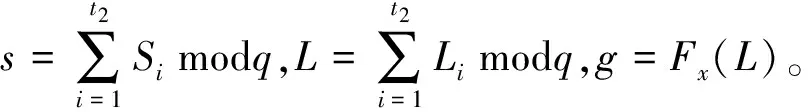
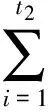
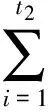
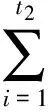
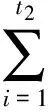
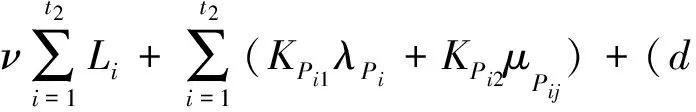
=νLmodq

因为g′=Fx(e1e2)modq=Fx(ν-1νL)=Fx(L)=g，所以多重签名有效。

2.2 安全性分析

2.2.1 可验证性

本文提出的基于ECC存在特权集的(t,n)门限群代理多重签名方案安全性主要依赖于椭圆曲线离散对数问题的难解性及hash函数单向性。由本文有关正确性证明知，代理授权份额的生成、单个签名的有效性、多重签名的生成都是可验证的，且正确。

2.2.2 强不可伪造性

代理授权份额(d,ν)的生成是由所有原始签名者和代理签名者共同合作完成，攻击者想要伪造授权份额(d,ν)，则必须要伪造签名者(原始签名者和代理签名者)的授权份额。假设攻击者想要伪造(DPi,ZPi)，由ZPi=dPi+fP(xPi)λPi+gP(yPij)μPij+(d⊕H(WM))rPimodq、DPi=dPiGmodq知，fP(xPi)、gP(yPij)为秘密份额，rPi、dPi为代理签名者选取的随机数，攻击者想要解出正确的(DPi,ZPi)，他必须知道dPi；而要得到正确的dPi，困难性相当于求解椭圆曲线离散对数问题。同理,(DUi，ZUi)也是不可伪造的，所以代理授权份额(d,ν)不能被伪造。

代理签名(g,s)不可伪造，由1.5节内容知代理签名是由t2个代理签名者且恰有t2′个特权集用户共同完成。若攻击者不知道(d，ν)，则就不可能伪造单个代理签名(Li,Si)；即使攻击者知道了(d,ν)，由Si=νli+fP(xPi)λPi+gP(yPij)μPij+(d⊕H(M))rPimodq、Li=liGmodq、RPi=rPiGmodq知，攻击者想要得到正确的li、rPi，问题依然是求解椭圆曲线离散对数问题。若攻击者获得了Pi的密钥，伪造了Pi对消息M的签名(Li,Si)，但SC只有在确认Pi的身份合法后才会接受Pi发送的单个签名，攻击者和SC身份交互认证时，SC就会发现提交签名的签名者的身份不合法，从而防止(Li,Si)被伪造。所以代理签名(g,s)不能被伪造。

KMC不能伪造Pi的签名。假设KMC和SC串通为签名者Pi生成WPi′、秘密份额KPi′，由Si=νli+fP(xPi)λPi+gP(yPij)μPij+(d⊕H(M))rPimodq知，KMC要伪造正确的单个签名，还必须知道签名者的li、rPi，KMC由Li=liGmodq、RPi=rPiGmodq求解li、rPi，困难性基于椭圆曲线离散对数问题。所以KMC无法伪造Pi的签名。

2.2.3 抗联合攻击

秘密份额的分发采用双秘密共享。代理授权过程中，用户进行联合攻击时，如果不符合t1′个特权用户的要求，即使有t1个或t1个以上的用户参与，由拉格郎日插值公式知，gO(yUij)不能被恢复，进而不能恢复群密钥；如果恰有t1′个特权用户，但不足t1个用户参与，fO(xUi)也不能被恢复。

类似代理签名生成过程中，用户进行联合攻击，如果不符合t2′个特权用户的要求，即使有t2个或t2个以上的用户参与，由拉格郎日插值公式知，gP(yPij)不能被恢复，进而不能恢复群密钥；如果恰有t2′个特权用户，但不足t2个用户参与，fP(xPi)也不能被恢复。所以本文方案抗联合攻击。

2.2.4 不可抵赖性

在代理签名生成过程中，代理签名者Pi对消息M的签名(Li,Si)加入了(d,ν)、随机数li、私钥rPi，签名验证过程中加入了所有代理签名者的公钥，所以代理签名者不能抵赖自己的签名。

2.2.5 特权集门限特性和匿名性

对原始签名群来说，原始签名者总数必须≥t1，且特权集中至少有t1′个原始签名者才能代表原始签名群体UO将签名权委托给代理签名群体UP。同理，对于代理签名群体UP来说，代理签名者总数必须≥t2，且特权集中至少有t2′个代理签名者才能代表群体UP对消息M进行签名。所以本文方案具有门限特性。

本文方案中所有签名者(原始签名者和代理签名者)都拥有自己的身份标志，秘密份额的生成与用户的真实身份无关，从而实现匿名性。

2.2.6 防陷害性

由强不可伪造知，攻击KMC、SC都无法代理签名者产生合法的单个签名。假设KMC和SC串通，成功生成代理签名者的单个签名，但不能达到陷害的目的。因为，设被陷害成员为Pi，KMC冒充Pi和SC执行成员加入协议，KMC选取随机数aPi′，计算APi′=aPi′Gmodq， SC为其生成WPi′，KMC为其分配秘密份额，并和原始签名与代理签名生成代理授权份额，选择随机数rPi′，生成单个签名(Li′,Si′)。Pi在遭到陷害后，向仲裁机构提交成员证书和认证公钥APi，证明自己被陷害。证明过程：

①仲裁机构随机选取k1，并发送给Pi。

②Pi收到k1，随机选取k2，计算y1=aPi(WPi‖k1‖k2)，并将y1、WPi、k2发送给仲裁机构。

2.3 安全性比较

方案从抗KMC伪造攻击、会话密钥安全性、抗联合攻击、特权集门限特性、匿名性等5个方面与引言中提到的文献[7, 8, 9, 12]相比较。安全性比较如表1所示。其中 “√” 表示具有该方面的安全性；“×”表示不具有该方面的安全性；“T1”代表抗KMC伪造攻击；“T2”代表会话密钥安全性；“T3”代表抗联合攻击；“T4”代表参与授权或代理签名的特权用户个数是否大于1；T5”代表匿名性。

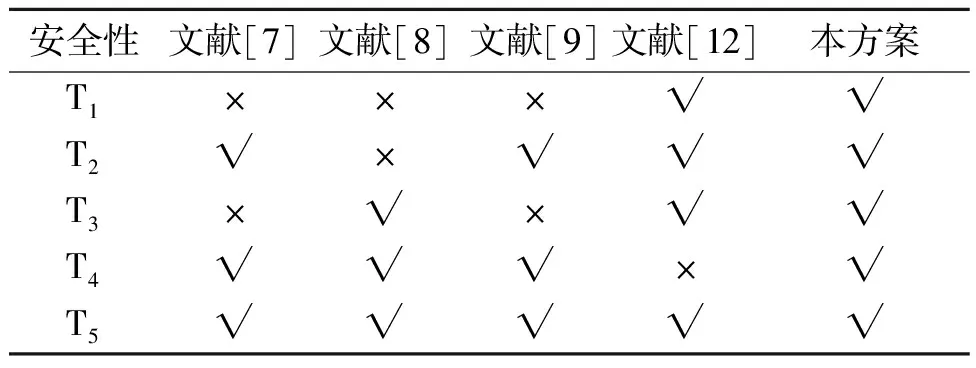
表1 安全性比较Table 1 Comparison of security

3 结束语

本文提出的基于ECC存在特权集的(t,n)门限群代理多重签名方案，安全性基于椭圆曲线离散对数问题的困难性、hash函数的单向性。签名生成使用了授权份额、秘密份额和认证密钥，有效防止了KMC和SC的串通陷害及代理签名者的抵赖。正确性分析表明，单个签名是有效的，多重签名生成正确可验证。安全性分析表明，该方案具有抗联合攻击、强不可伪造性、不可抵赖性、特权集门限特性和匿名性等安全属性，具有一定的实际应用价值。

[1] Desmedt Y, Frankel Y. Shared generation of authenticators and signatures[C]//Advances in Cryptology-CRYPTO’91. Berlin: Springer-Verlag, 1992: 457-469.

[2] Harn L. Group-oriented (t,n) threshold digital signature scheme and digital multi-signature[J]. IEEE Proceedings of Computers and Digital Techniques, 1994, 141(5): 307-313.

[3] Wang C T, Lin C H, Chang C C. Threshold signature schemes with traceable signatures in group communications[J]. Computer Communication, 1998, 21(8): 771-776.

[4] Shi Yi. Design and analysis of a new group of (tj,t,n) threshold group-signature scheme[J]. Journal of the Graduate School of the Chinese Academy of Science, 2001, 18(2): 110-113.

[5] Li L H, Tzeng S F, Hwang M S. Generalization of proxy signature based on discrete logarithms[J]. Computers & Security, 2003, 22(3): 245-255.

[6] Chen W D, Fen D G. A group of threshold group-signature schemes with privilege subsets[J]. Journal of Software, 2005, 16(7): 1289-1295.

[7] 谭作文,刘卓军，陈伟东.存在特权集的代理门限群签名方案[J].计算机工程与应用,2004，40(25):31-34. Tan Z W, Liu Z J, Chen W D. Proxy threshold group-oriented signature schemes with privileged subsets[J]. Computer Engineering and Applications, 2004, 40(25): 31-34. (in Chinese)

[8] 王天芹．存在特权集的门限代理群签名方案[J]．计算机应用研究，2008，25(7):2146-2147． Wang T Q. Threshold proxy group-signature scheme with privilege subsets[J]. Application Research of Computers, 2008, 25(7): 2146-2147. (in Chinese)

[9] 杨长海,唐西林.具有多种特性的门限多代理多签名方案[J].计算机工程,2009,35(13): 160-162. Yang C H, Tang X L. Threshold multi-proxy and multi-signature schemes with various characteristics[J]. Computer Engineering, 2009, 35(13): 160-162. (in Chinese)

[10] 董玉蓉,汪学明.一种改进的存在特权集的门限群签名方案[J].计算机工程与科学,2011,33(4):13-16. Dong Y R, Wang X M. An improved threshold group signature scheme with a privilege set[J]. Computer Engineering & Science, 2011, 33(4): 13-16. (in Chinese)

[11] 陈道伟,施荣华,樊翔宇.一种存在特权集门限群代理多重签名方案[J].小型微型计算机系统,2012,33(11):2514-2517. Chen D W, Shi R H, Fan X Y. Threshold group-proxy multi-signature schemes based on privilege subsets[J]. Journal of Chinese Computer Systems, 2012, 33(11): 2514-2517. (in Chinese)

[12] 李志敏,王勇兵.有特权者的门限代理签名方案[J].西北师范大学学报(自然科学版),2013,49(3):46-50. Li Z M, Wang Y B. Threshold proxy signature scheme with the privileged[J]. Journal of Northwest Normal University (Natural Science Edition), 2013, 49(3): 46-50. (in Chinese)

[13] 汤鹏志,郭红丽,何涛.基于双线性的有特权集门限代理签名方案[J].合肥工业大学学报(自然科学版),2014,37(9):1063-1066. Tang P Z, Guo H L, He T. Threshold proxy signature scheme with privileged subset based on bilinearity[J]. Journal of Hefei University of Technology (Natural Science Edition), 2014, 37(9): 1063-1066. (in Chinese)

[14] 曹阳,洪歧,陈勇,等.一种基于ECC具有时间限制的动态秘密共享方案[J].重庆邮电大学学报(自然科学版),2014,26(4):556-558. Cao Y, Hong Q, Chen Y,etal. A time-limited dynamic secret-sharing scheme based on ECC[J]. Journal of Chongqing University of Posts and Telecommunications, 2014, 26(4): 556-558. (in Chinese)

A(t,n)thresholdgroup-proxymulti-signatureschemewithprivilegesubsetsbasedonECC

CAO Yang

SchoolofMathematicsandComputerScience,ShaanxiUniversityofTechnology,Hanzhong723000,China

In order to solve the problems of joint attack, forgery attack, permissions and denial in the threshold group signature scheme, this paper puts forward a (t,n) threshold group-proxy multi-signature scheme with privilege subsets of ECC, based on the unidirectional hash function and the intractability of the elliptic curve discrete logarithm problem, and combined with Shamir (t,n) threshold scheme, which meets the features of ((t1′,n1′;t1,n1)(t2′,n2′;t2,n2)) threshold. By means of interactive authentication under the public key environment, the scheme adds the member authentication key so as to effectively prevent the collusion between key management center and signature server. The signer verifies whether the secret share distributed by management center is effective through the equation; the agent authorized share is generated by the original signer and the proxy signer together, and the single signature is produced by using the signer’s private key and random numbers, and this effectively prevent denial. The safety analysis shows that the scheme has merits of resisting the joint strikes, strong unforgeability, threshold peculiarity and anonymity, and it can meet the due nature of threshold group-proxy signature.

privilege subsets; (t,n) threshold group-proxy; multi-signature; ECC

TP393 [

] A

10.3969/j.issn.1671-9727.2017.05.12

1671-9727(2017)05-0623-08

2016-06-02。

国家自然科学基金项目(21373132)； 陕西省教育厅科研计划项目(17JK0148)。

曹阳(1978-)，女，硕士,讲师，研究方向：信息安全与计算机应用, E-mail:cyang0618@sina.com。